使用R语言对时间序列构建AR§和MA(q)模型 - 以CPI数据为例
在King’s College London学习FA,一门课的project,这里只附上代码和结果,报告就没有了。使用的数据是美国、日本、希腊的CPI月度数据,从2010年1月到2021年8月,放在一个CSV文件里。(本文以美国为例,实际上做了三个国家,但是过程都差不多,所以就只写一个了。)
首先是读入文件
# Remove all items from memory (if any)
rm(list=ls(all=TRUE))
# Set the working directory to load files
setwd("filepath") #这里是csv文件以及你的代码存放的位置
library("lmtest") #做回归的包
library("tseries") #做时间序列的包
# 上面两个包如果没有需要安装
# install.packages("tseries")
# load data
indexs <- read.csv("data.csv", header=TRUE, encoding="UTF-8")
# 读入文件,我的文件有4列,第一列是时间,2-4列是三个国家的CPI数据
indexs <- as.martix(indexs)
d <- as.Date(indexs[,1])
indexs <- apply(indexs[,2:NCOL(indexs)],2,as.numeric)
rownames(indexs) <- as.character(d)
indexs <- ts(indexs, start=c(2010,01),end=c(2021,08),frequency=12)
# 将数据以时间序列表示
随后对数据进行调整,首先要去除季节性趋势,随后的逻辑是我们需要找到一个稳定的数据进行建模(关于为什么需要用稳定的数据进行建模请参考各类金融计量经济学教材)。
datacomponent1 <- decompose(indexs[,1],type="additive")
plot(datacomponent1) # 查看分解的结果
usacpi <- indexs[,1]-datacomponent1$seasonal # 去除掉季节性因素
plot(usacpi,main="seasonal-adjusted monthly CPI of USA",ylab="",xlab="")
acf(usacpi) # 画acf图
adf.test(usacpi) # 对美国CPI数据进行adjusted Dicky Fuller 检验
对CPI的分解结果如下:
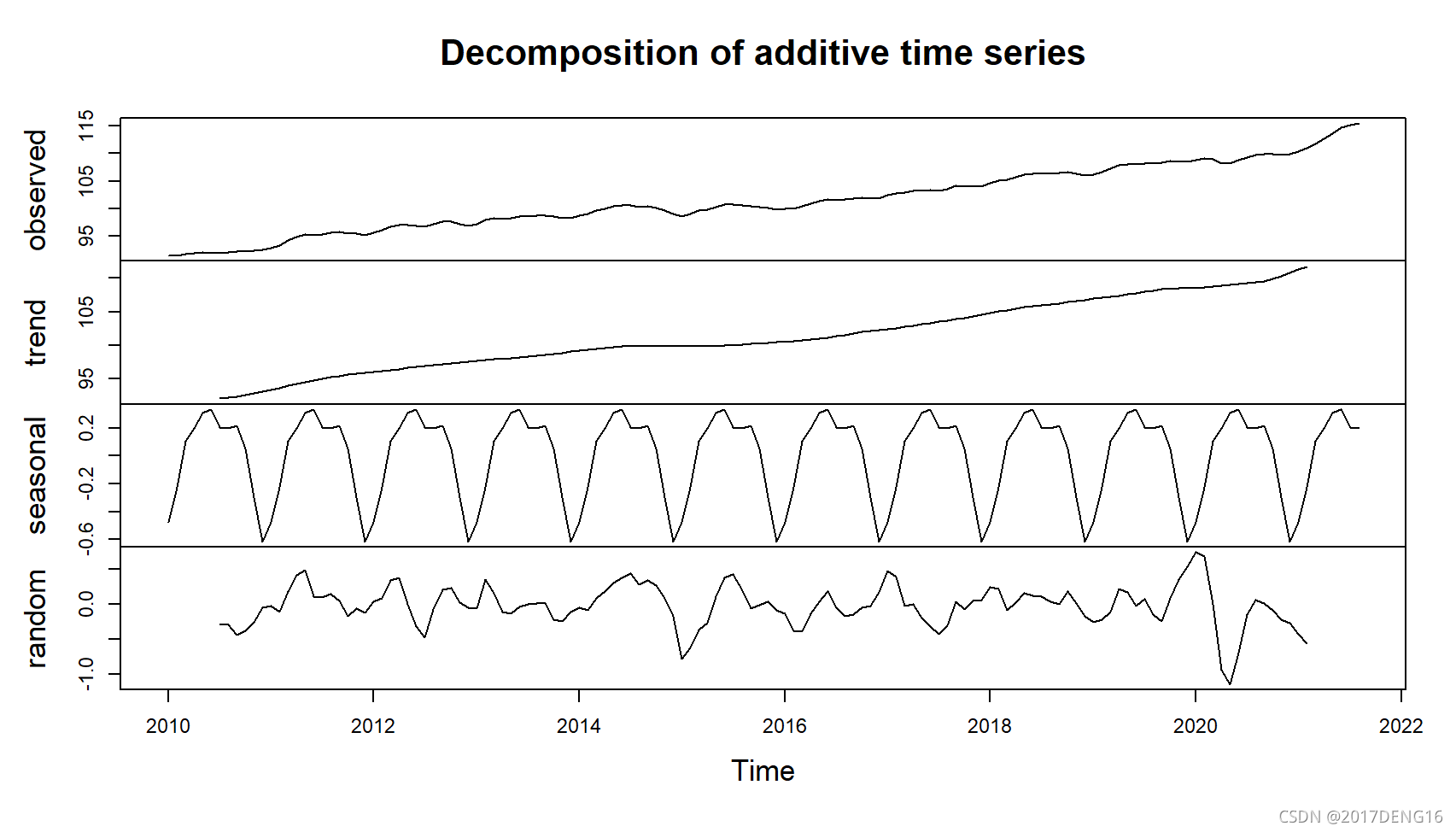
得到季节性调整后的CPI数据
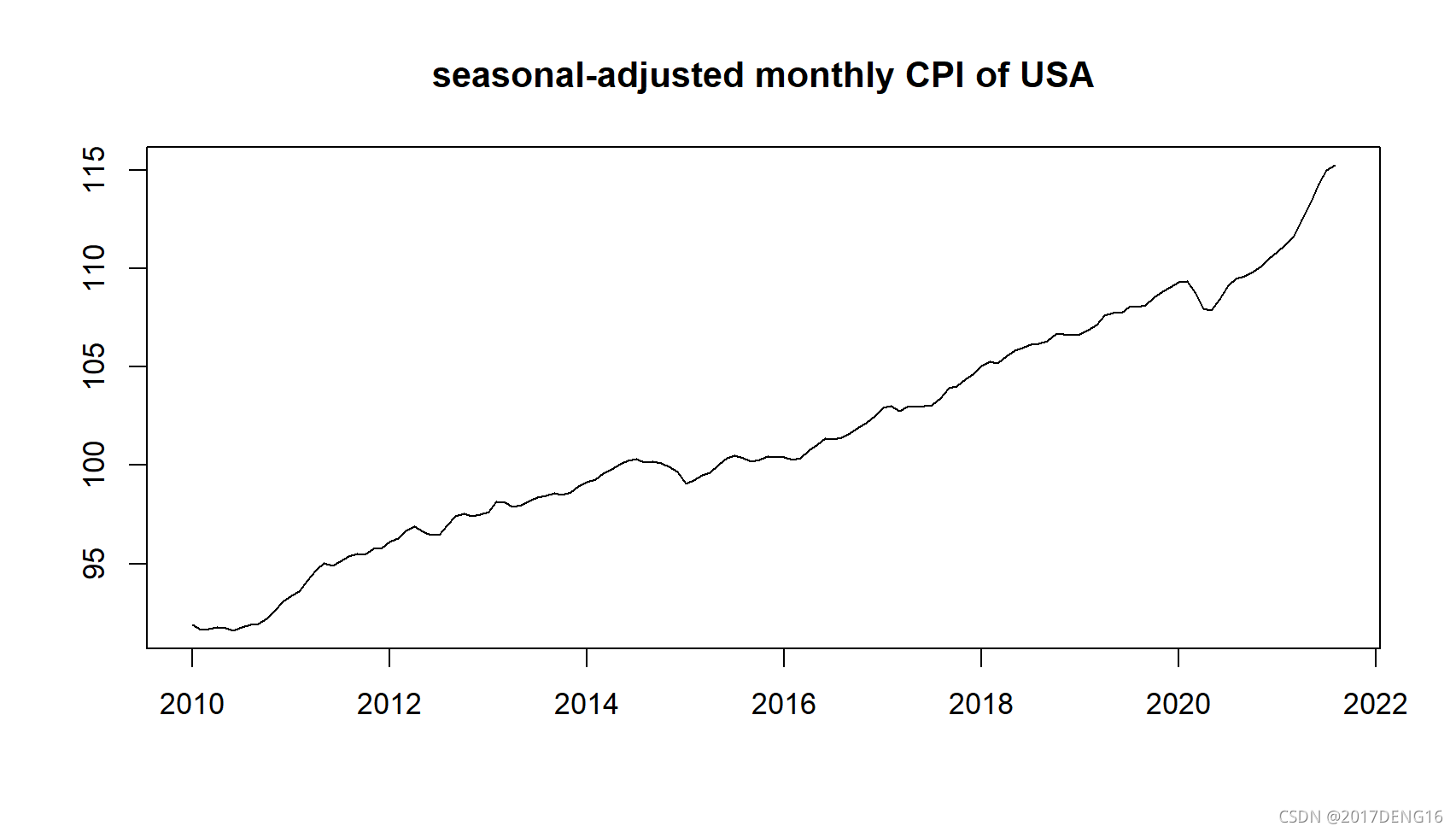
可以看出CPI数据有变化的均值,存在增长趋势,是不平稳的数据。
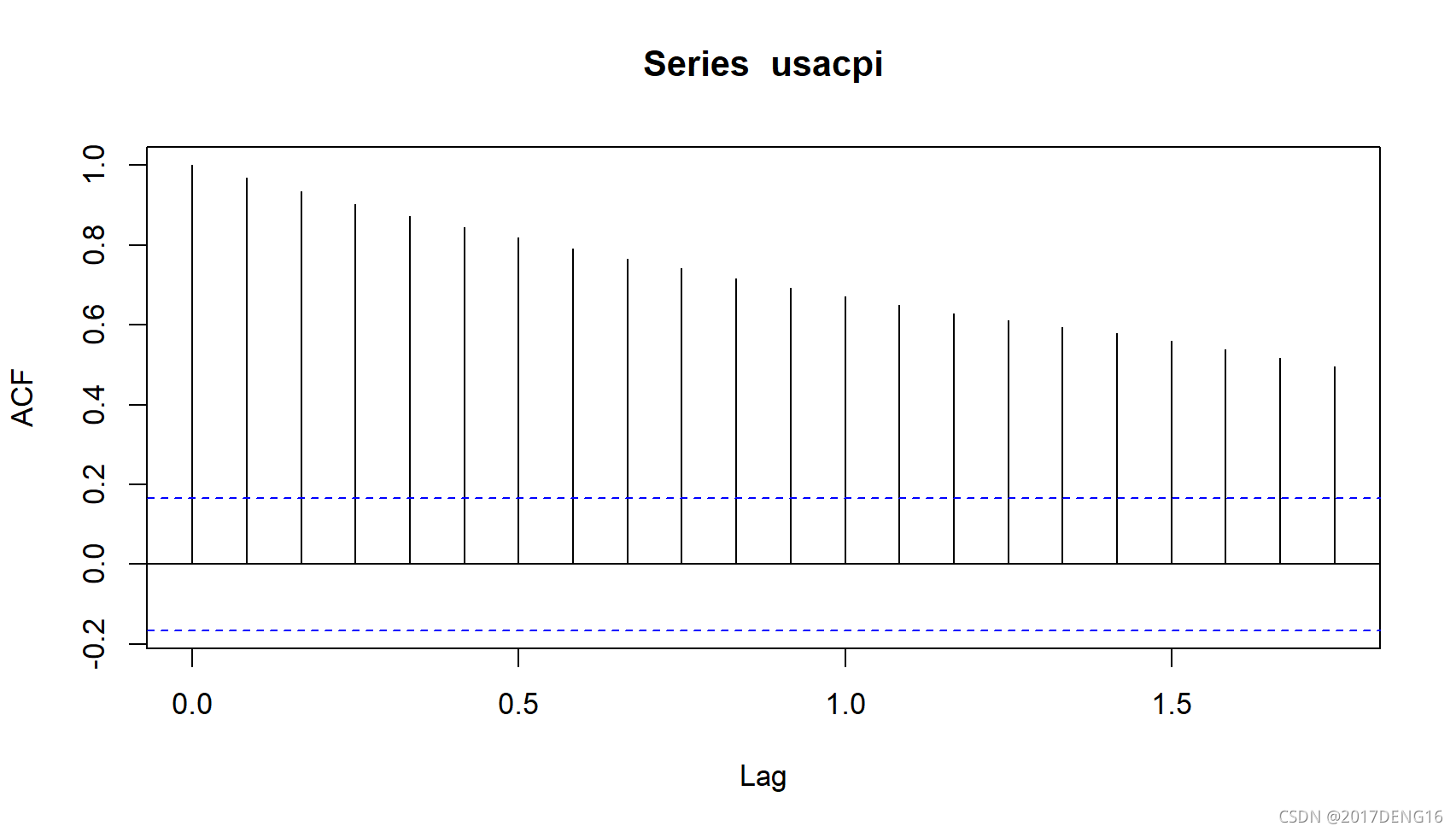
可以看出acf有系数很高且缓慢下降的趋势,所以是非平稳的(实际上的逻辑是滞后项的系数之和大于1可看做非平稳的。这里的滞后阶数有点问题,是以年为单位的,所以各位将就看看,懂得都懂)
同时ADF test的结果为:
Augmented Dickey-Fuller Test
data: usacpi
Dickey-Fuller = -0.8484, Lag order = 5,
p-value = 0.9551
alternative hypothesis: stationary
p-value > .05,故在95%置信度上不能拒绝原假设(不平稳)
于是对CPI数据进行如下调整:
(实际上的逻辑应当是指数不符合正态分布,于是经济学家想出增长率这种东西,增长率就可以取到负值,更贴合正态分布,所以用log return这种,而不是像这里说的这样毫无逻辑地做log和diff,但是老师这样教的,我们就这样做了。)
log1 <- log(usacpi)
plot(log1,type="l")
acf(log1)
# 同样看出不平稳做了一阶差分
y1 <- diff(log1)
plot(y1)
acf(y1)
Box.test(y1,lag=1,type="Ljung-Box")
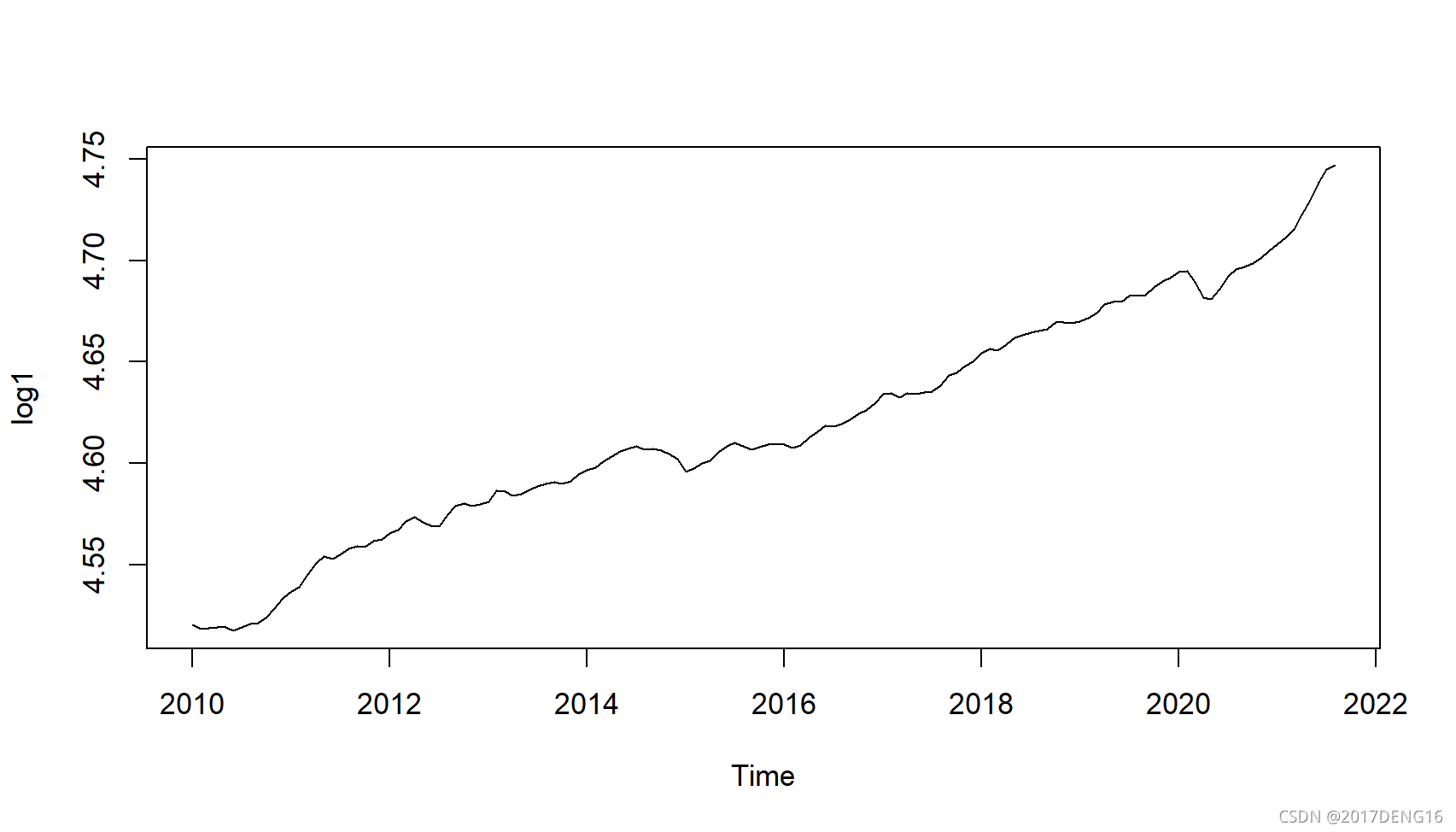
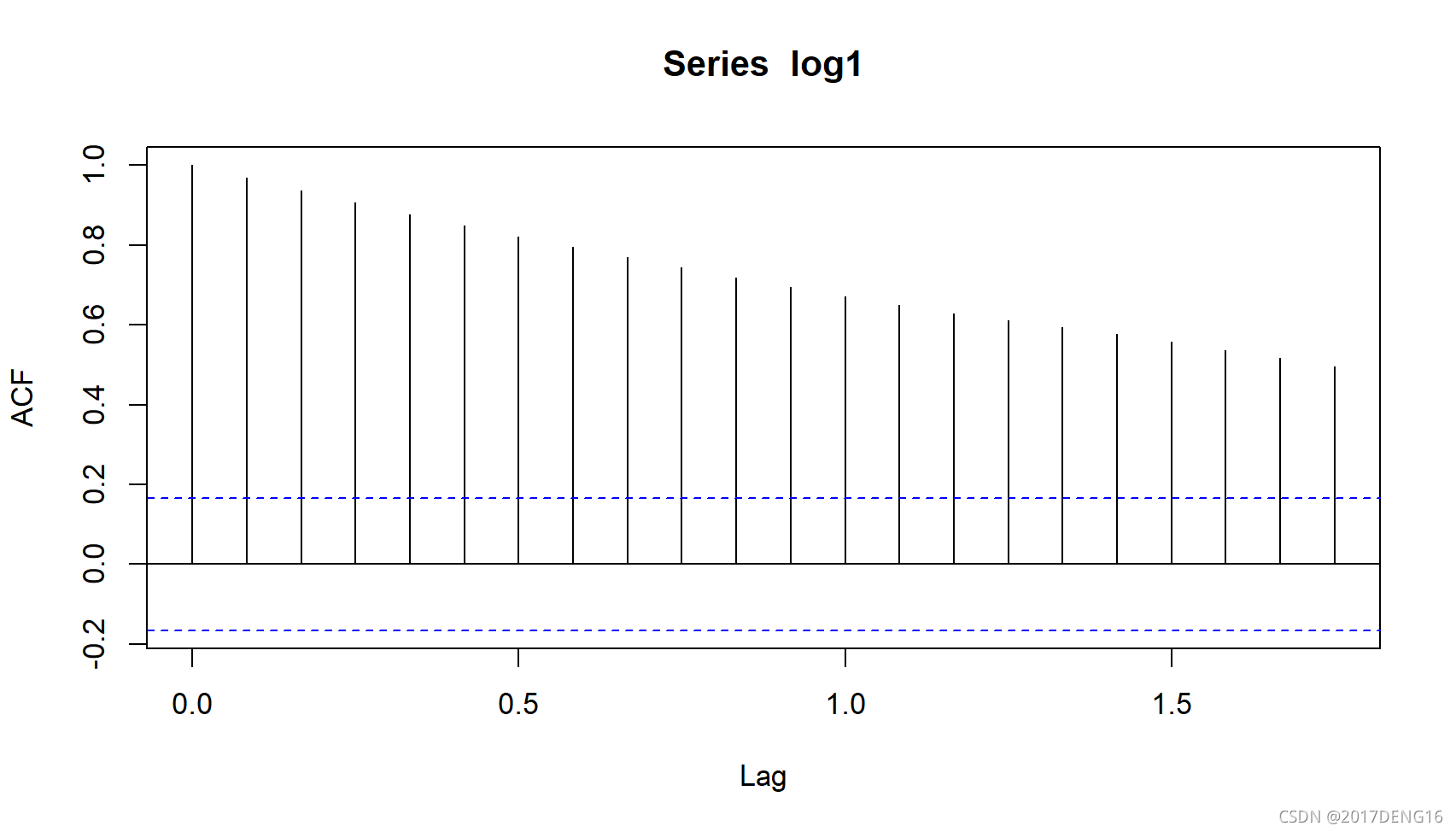
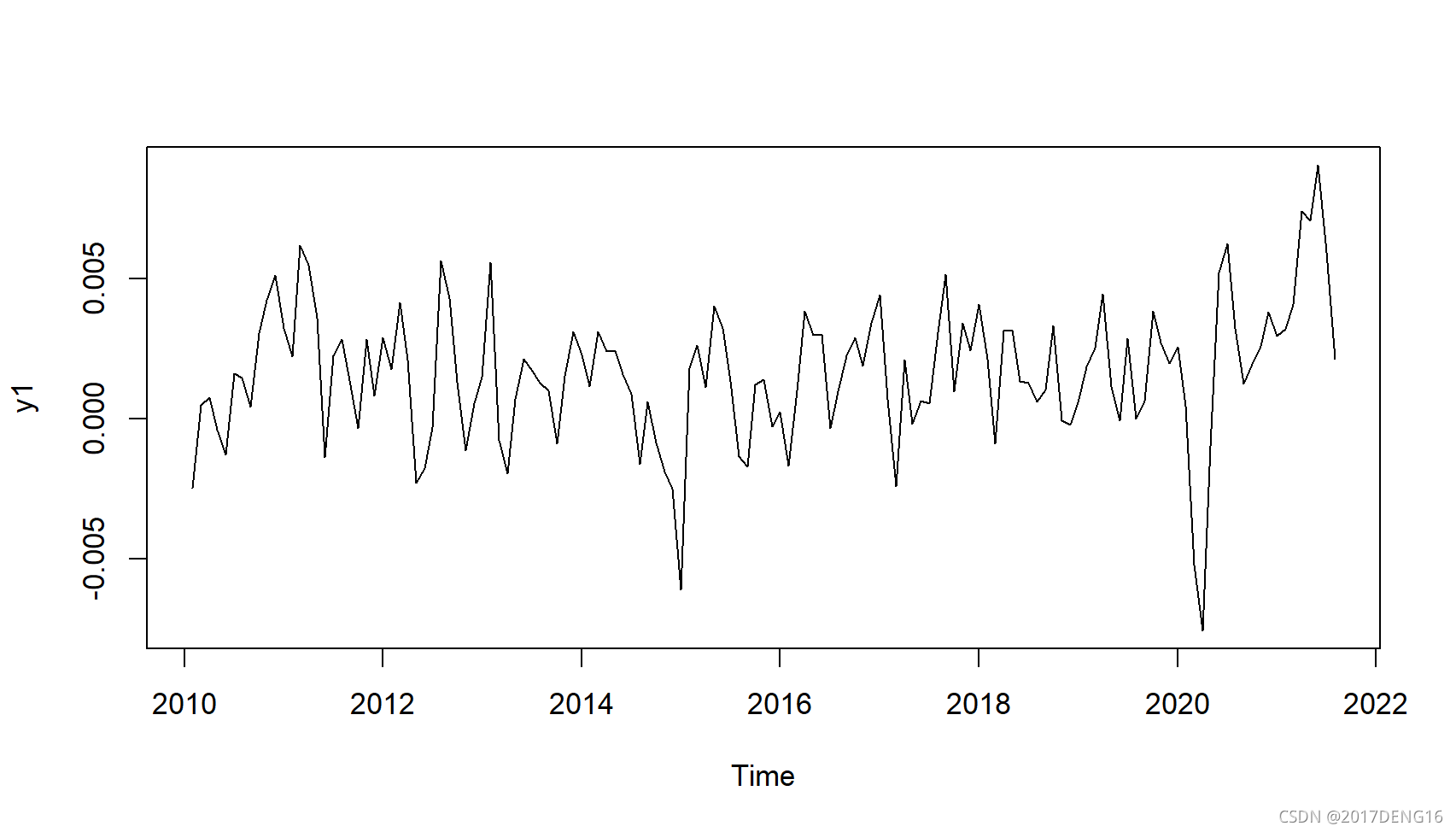
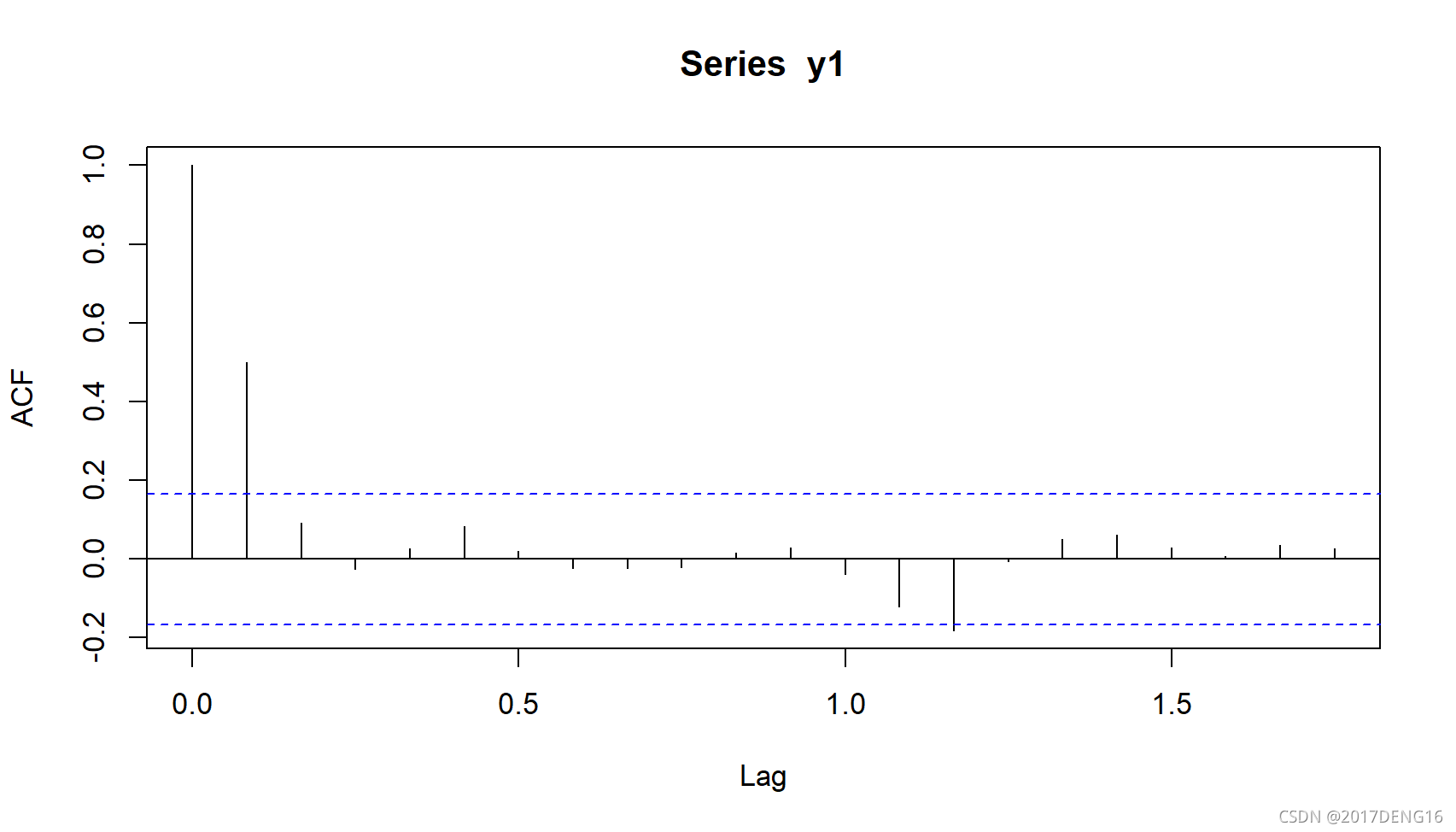
很明显从log增长率的acf就可以看出log inflation是弱平稳的。
并且,BOX 检验的结果为
Box-Ljung test
data: y1
X-squared = 35.37, df = 1, p-value =
2.727e-09
可以看出p值很小(df值越大p值越小),故不能拒绝原假设,表明不是白噪声过程。
首先我们考虑WN过程(虽然明显可以从acf看出不服从WN过程,BOX检验又拒绝了原假设,但是老师就是这个流程所以也做了。)
这里WN过程建立的模型是
?
y
t
=
u
t
+
α
?
.
\ y_t = u_t + α \,.
?yt?=ut?+α.
out1 <- lm(y1~1)
summary(out1)
u1 <- out1$residuals #取模型的残差
acf(u1)
回归的结果是
Call:
lm(formula = y1 ~ 1)
Residuals:
Min 1Q Median 3Q Max
-0.0091765 -0.0011694 -0.0000182 0.0014419 0.0073961
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0016273 0.0002086 7.802 1.36e-12 ***
可以看出有明显的截距项
对残差画acf图:
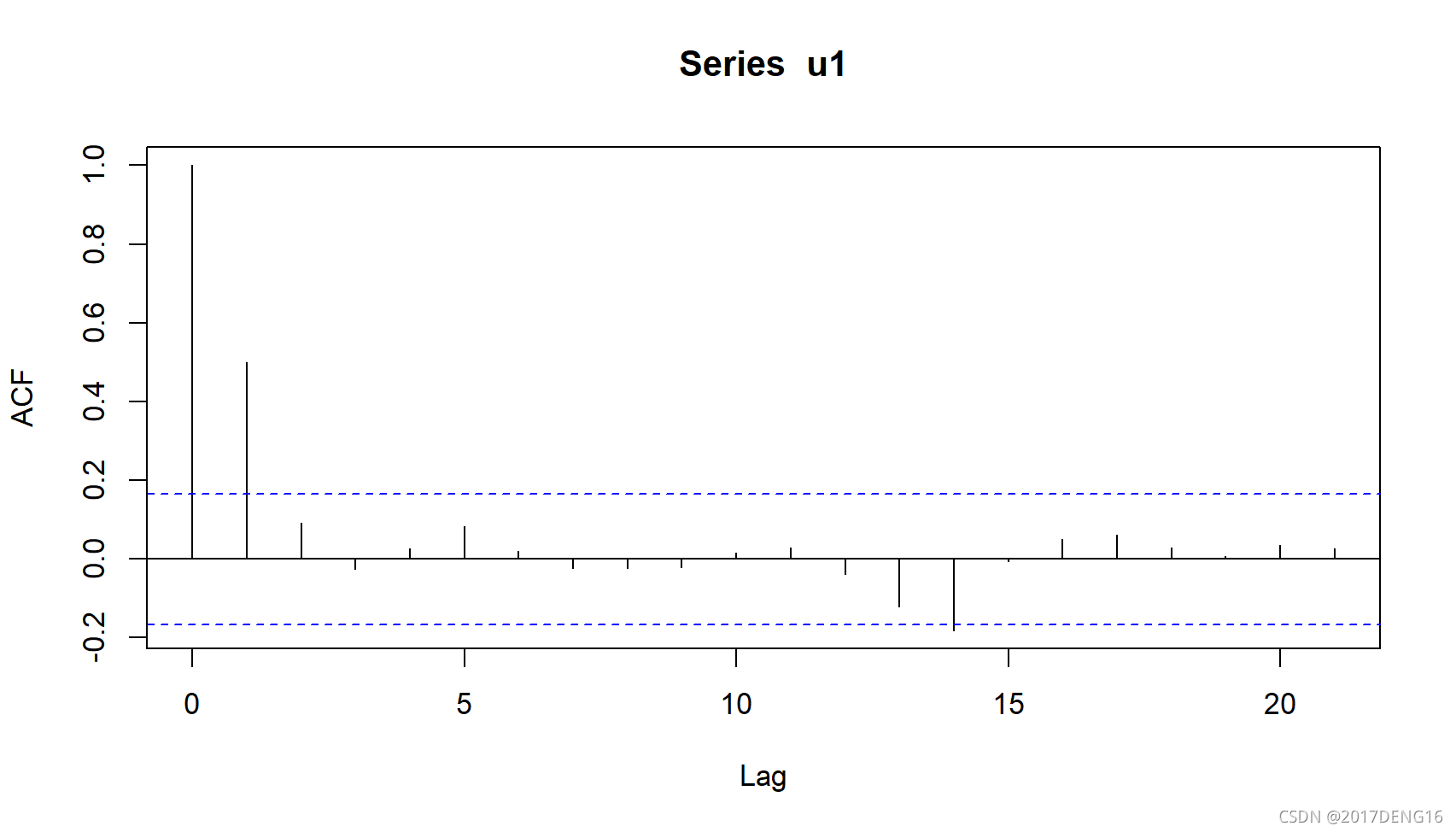
其实跟直接用log inflation做有什么区别呢,但是老师就是说要用残差的acf来判断MA模型要做滞后几阶,这里我们看到滞后1阶明显查出来区间,所以我们先做MA(1)。有些朋友就要问了,这个滞后14阶好像也出了为什么不做滞后14阶呢,这里简单解释一下,做MA模型和AR模型的逻辑是寻找历史数据的持续性,即历史数据对未来的影响,一般来说都是离得近的影响更大,如果是之前一个月两个月三个月对这个月有影响非常好理解,但是如果上上个月的没有影响反而半年前的有影响这就很难理解,这不就是属于季节性的影响了吗,所以在选择滞后阶数的时候,出现不显著的滞后阶数系数,我们就舍弃该模型。
# 首先考虑MA(1)模型
m1 <- arima(y1,order=c(0,0,1))
coeftest(m1) #结果显著所以我们增加滞后项看滞后2阶是否显著
# MA(2)
m2 <- arima(y1,order=c(0,0,2))
coeftest(m2) #同样显著,所以我们继续增加
# MA(3)
m3 <- arima(y1,order=c(0,0,3))
coeftest(m14) #滞后三阶不显著
# use MA(2)
#如果截距项不显著这里应该使用如下代码
# ma1 <- arima(y1,order=c(0,0,2)include.mean=FALSE)
ma1 <- arima(y1,order=c(0,0,2))
coeftest(ma1) #这是以防去除掉截距项会影响参数而做的测试,这里因为有截距项不展示结果,就和上面的m2一样
MA(1)系数
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
ma1 0.53737444 0.06467794 8.3085 < 2.2e-16 ***
intercept 0.00161270 0.00028516 5.6554 1.554e-08 ***
MA(2)系数
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
ma1 0.61970994 0.08264944 7.4981 6.477e-14 ***
ma2 0.17640829 0.09254276 1.9062 0.05662 .
intercept 0.00160241 0.00032486 4.9327 8.111e-07 ***
(这里ma2只在90%的置信度上显著,如果选择95%则应当舍去)
MA(3)系数
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
ma1 0.61992424 0.08778301 7.0620 1.641e-12 ***
ma2 0.17675004 0.10716869 1.6493 0.09909 .
ma3 0.00058488 0.08136832 0.0072 0.99426
intercept 0.00160213 0.00032508 4.9285 8.287e-07 ***
此时我们得到的模型是
?
y
t
=
u
t
+
0.6197
u
t
?
1
+
0.1764
u
t
?
2
+
0.0016
?
.
\ y_t = u_t + 0.6197u_{t-1} + 0.1764u_{t-2} + 0.0016 \,.
?yt?=ut?+0.6197ut?1?+0.1764ut?2?+0.0016.
随后构建AR模型,使用pacf
pacf(y1)
# AR(2)
m4 <- arima(y1,order=c(2,0,0))
coeftest(m4)
# AR(3)
m5 <- arima(y1,order=c(3,0,0))
coeftest(m5)
# use AR(2)
ar1 <- arima(y1,order=c(2,0,0))
#这里如需去除截距项方法和MA一样
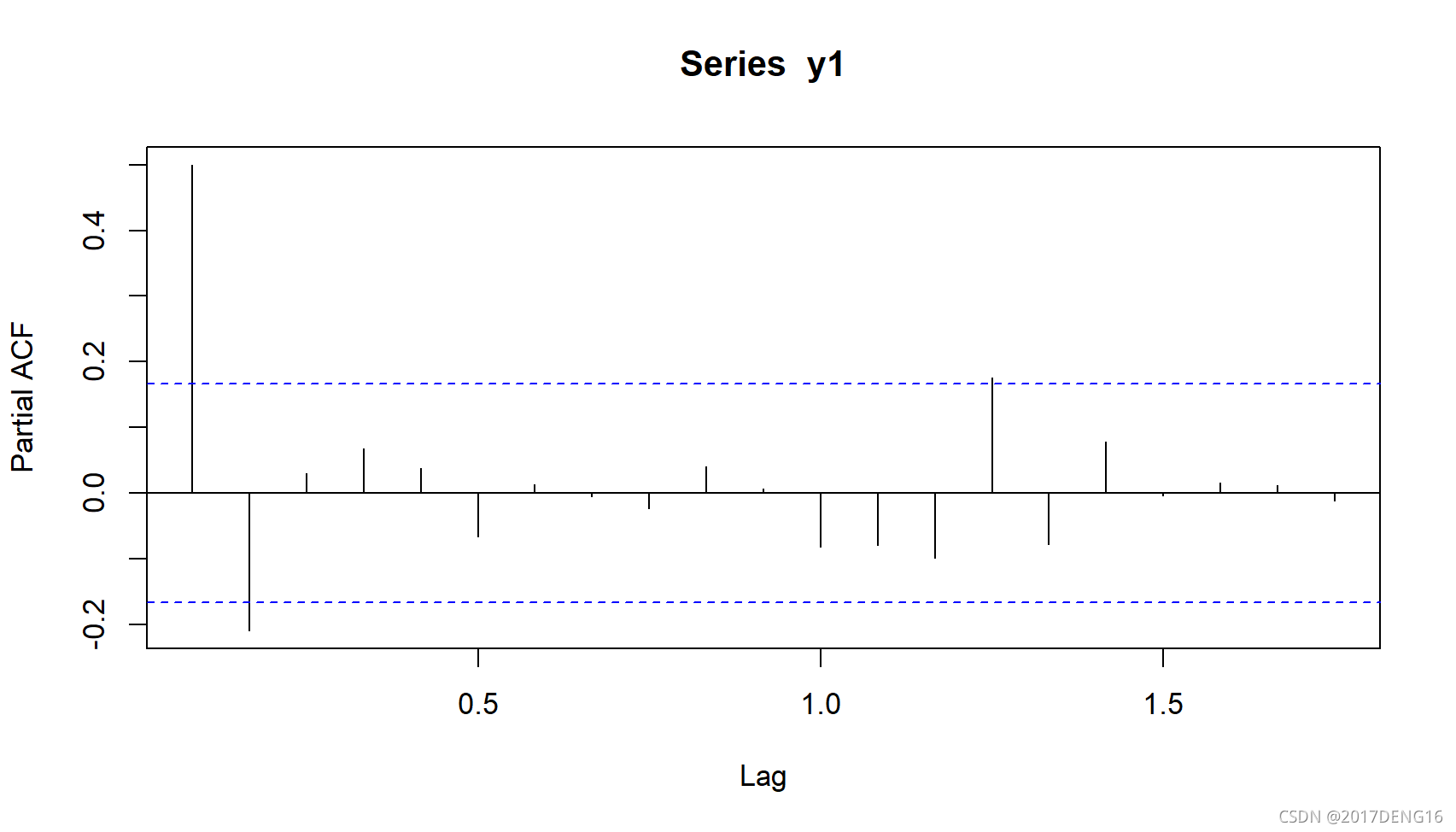
acf是从第二根线开始算,但pacf是从第一根线开始算,所以可以看出滞后1阶有正的相关性,2阶有负的相关性,且都超出了区间,所以AR模型从AR(2)开始构建
AR(2)系数
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
ar1 0.61648118 0.08349852 7.3831 1.546e-13 ***
ar2 -0.21909059 0.08419508 -2.6022 0.009263 **
intercept 0.00160193 0.00030232 5.2988 1.166e-07 ***
AR(3)系数
z test of coefficients:
Estimate Std. Error z value Pr(>|z|)
ar1 0.62334247 0.08542500 7.2970 2.944e-13 ***
ar2 -0.23838759 0.09849912 -2.4202 0.01551 *
ar3 0.03313291 0.08789615 0.3770 0.70621
intercept 0.00160334 0.00031185 5.1414 2.727e-07 ***
可以看出滞后3阶不显著,所以使用AR(2)
此时我们得到的模型是
?
y
t
=
0.0016
+
0.6165
y
t
?
1
?
0.2191
y
t
?
2
+
u
t
?
.
\ y_t = 0.0016 + 0.6165y_{t-1} - 0.2191y_{t-2} + u_t \,.
?yt?=0.0016+0.6165yt?1??0.2191yt?2?+ut?.
随后使用AIC和HBIC比较AR和MA模型(因为做的是三个国家,所以这里比较的时候用了六个模型,但是另外两个国家构建的过程本文并未包括,大家如果要使用记得自行调整)
aicpair <- c(AIC(ma1),AIC(ma2),AIC(ma3),AIC(ar1),AIC(ar2),AIC(ar3))
aicpair <- matrix(aicpair,nrow=3,ncol=2,dimnames=list(c("index1","index2","index3"),c("MA","AR")))
aicpair
bicpair <- c(BIC(ma1),BIC(ma2),BIC(ma3),BIC(ar1),BIC(ar2),BIC(ar3))
bicpair <- matrix(bicpair,nrow=3,ncol=2,dimnames=list(c("index1","index2","index3"),c("MA","AR")))
bicpair
AIC的结果为
| country | MA | AR |
|---|---|---|
| usa | -1315.783 | -1315.842 |
| greece | -1085.546 | -1102.073 |
| japan | -1257.006 | -1256.986 |
HBIC的结果为
| country | MA | AR |
|---|---|---|
| usa | -1304.045 | -1304.104 |
| greece | -1079.677 | -1093.270 |
| japan | -1251.137 | -1251.117 |
选择指标更小的模型作为最终模型,over
(如有错别字请多原谅)