[游戏开发]游戏图形学(UE4)（更新中）

前言：最近看了好多大佬的视频和文章，赞叹之余，做些记录。

参考资料

https://www.bilibili.com/video/BV1X7411F744
https://www.bilibili.com/video/BV1Qi4y1g7xG
https://www.notion.so/GAMES101-b0e27c856cde429b8672671a54c34817

数学知识

简单记录

向量

点积

公式

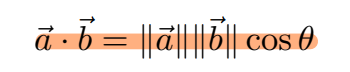
性质

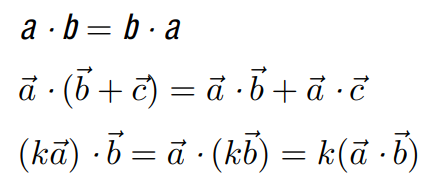
矩阵表示

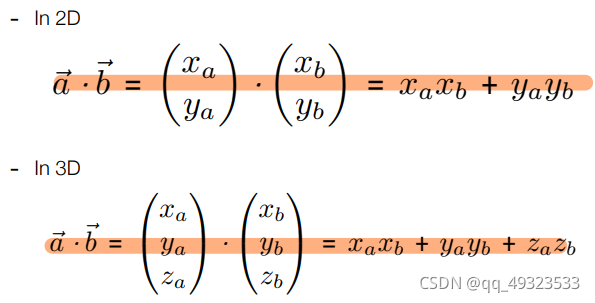
在图形学中作用：
判断两个方向之间的大小：cos大小
分解向量
确定前后：cos正负

叉积

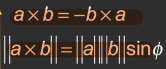
性质：

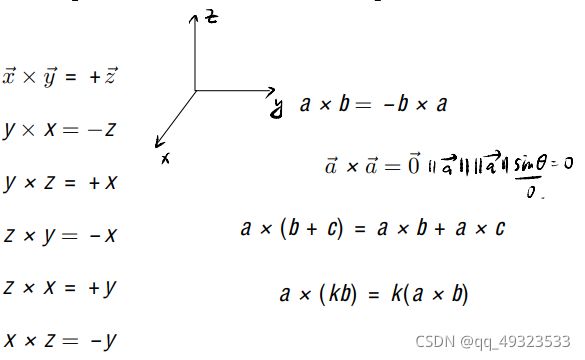
矩阵表示：

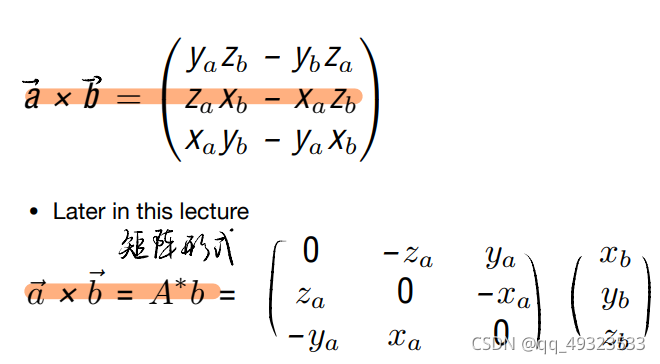
作用：
建立直角坐标系：X轴 x Y轴 = Z轴（右手系）
判定左右
判定图形内外

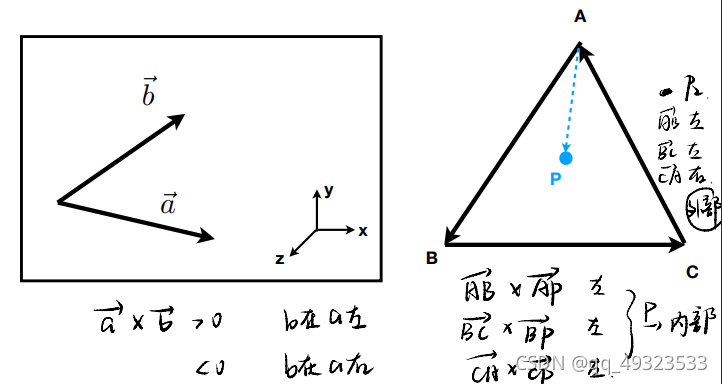
分解向量

Eigen线性代数运算库

Eigen::Vector3f u(1.0f,2.0f,3.0f);//向量定义
Eigen::Vector3f v(1.0f,0.0f,0.0f);
v + w ; //向量求和
 2.0f * v ;//向量数乘

 Eigen::Matrix3f i,j;//矩阵定义
 i << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
 j << 2.0, 3.0, 1.0, 4.0, 6.0, 5.0, 9.0, 7.0, 8.0;
i + j//矩阵加减
i * 2.0//矩阵数乘
i * j//矩阵乘法
i * v//矩阵乘向量

矩阵

矩阵的转置：

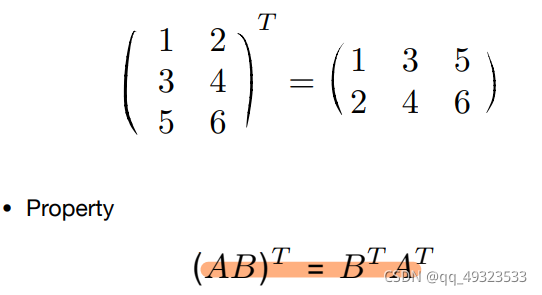
基础变换：
线性变换 = 旋转 + 缩放 + 切变
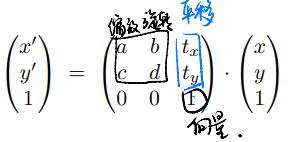
仿射变换 = 线性变换 + 平移变换

三元数表示二维矩阵

四元数表示三维变换：

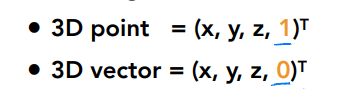
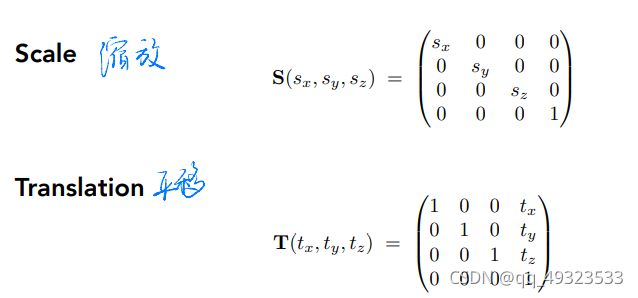
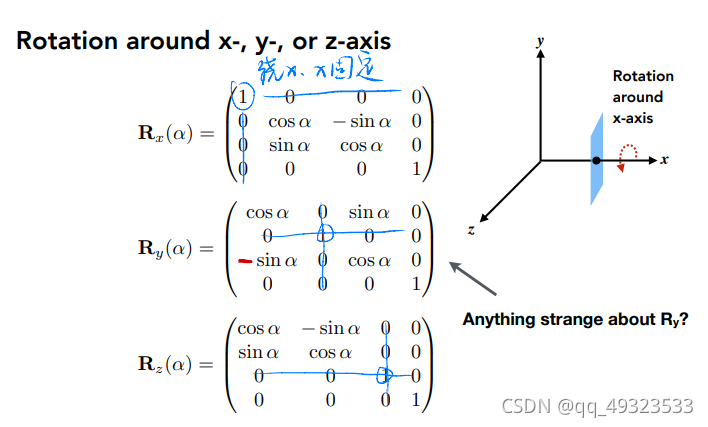
欧拉角表示旋转
row pitch yaw ：绕x,y,z轴旋转

绕n轴旋转α角

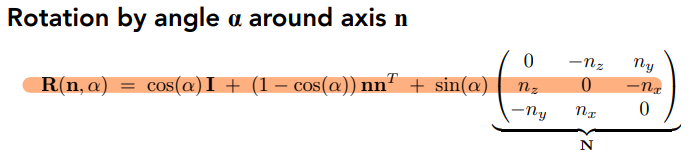
若绕静坐标系（世界坐标系）旋转，则左乘，也是变换矩阵坐标矩阵；若是绕动坐标系旋转（自身建立一个坐标系），则右乘，也就是坐标矩阵变换矩阵。 即，左乘是相对于坐标值所在的坐标系（世界坐标系）下的三个坐标轴进行旋转变换。而右乘则是以当前点为旋转中心，进行旋转变换。

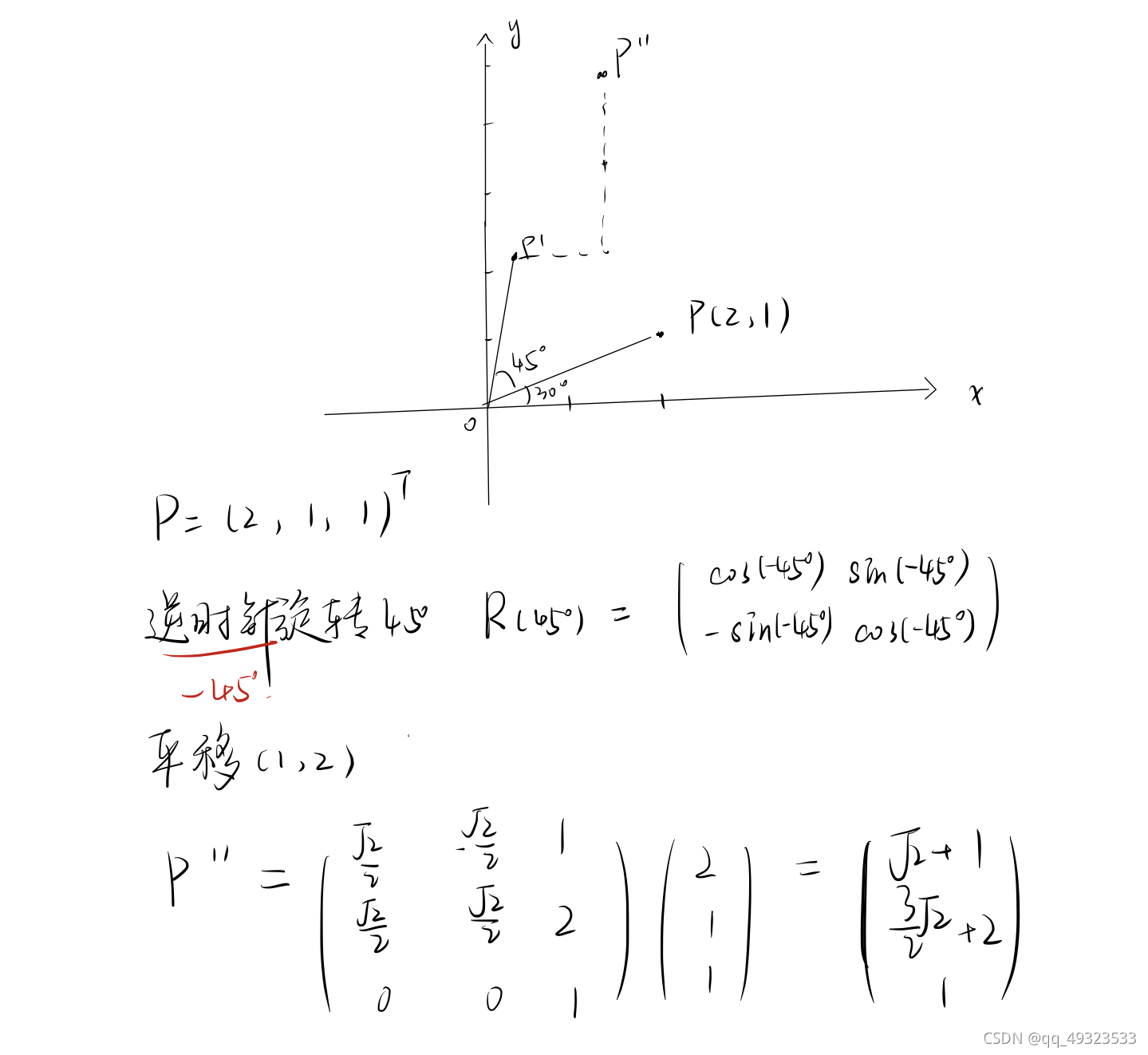
例题

给定一个点 P=(2,1), 将该点绕原点先逆时针旋转 45?，再平移 (1,2), 计算出变换后点的坐标（要求用齐次坐标进行计算）。

#include<cmath>
#include <Eigen/Core>
#include <Eigen/Dense>
#include <iostream>

//分步版本
void Transformation_1() {
    Eigen::Vector3d v(2.0f, 1.0f, 1.0f);
    Eigen::Matrix3d rotate;
    Eigen::Matrix3d tranform;
    double r = -45.0 / 180.0 * acos(-1);//把角度转换成弧度
    rotate << cos(r), sin(r), 0,
            -1.0f * sin(r), cos(r), 0,
            0, 0, 1;
    tranform << 1, 0, 1,
                0, 1, 2,
                0, 0, 1;

    //两次左乘
    v = rotate * v;
    v = tranform * v;
}

//总变换矩阵
void Transformation_2() {
    Eigen::Vector3d v;
    Eigen::Vector3d trans;
    double r = -45.0 / 180.0 * acos(-1);
    trans << cos(r),sin(r),1,
            -1.0f * sin(r), cos(r), 2,
            0, 0, 1;
    v = trans * v;
}

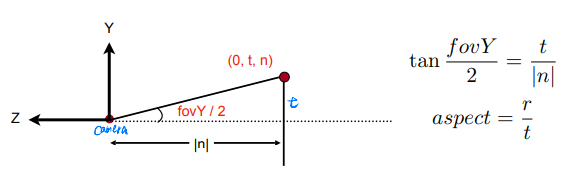
MVP变换

Model transformation（模型变换）：用一个变化矩阵把actor的顶点坐标从Local坐标系（相对）转换到世界Global坐标系（绝对）。

View transformation（视口变换）：将世界坐标系转换到摄像机坐标系

Projection transformation（投影变换）：找到屏幕，把Actor平移缩放到屏幕上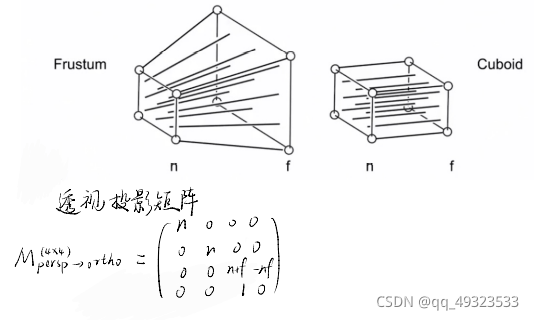

例题

填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个点 v0(2.0, 0.0, ?2.0), v1(0.0, 2.0, ?2.0), v2(?2.0, 0.0, ?2.0), 你需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形 (在代码框架中，我们已经提供了 draw_triangle 函数，所以你只需要去构建变换矩阵即可)。简而言之，我们需要进行模型、视图、投影、视口等变换来将三角形显示在屏幕上。在提供的代码框架中，我们留下了模型变换和投影变换的部分给你去完成。
在本次作业中，因为你并不需要去使用三角形类，所以你需要理解修改的文件为:rasterizer.hpp 和 main.cpp。其中 rasterizer.hpp 文件作用是生成渲染器界面与绘制。

#include "Triangle.hpp"
#include "rasterizer.hpp"
#include <eigen3/Eigen/Eigen>
#include <iostream>
#include <opencv2/opencv.hpp>

constexpr double MY_PI = 3.1415926;

//模型变换
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

	//绕z轴旋转矩阵
	double r = rotation_angle / 180.0*acos(-1);
	Eigen::Matrix4f translate;
	translate<<cos(r),(-1)*sin(r),0,0,
				sin(r),cos(r),0,0,
				0,0,1,0,
				0,0,0,1;
	model = translate * model;
    return model;
}

//视图变换
Eigen::Matrix4f get_view_matrix(Eigen::Vector3f eye_pos)
{
	Eigen::Matrix4f view = Eigen::Matrix4f::Identity();
	Eigen::Matrix4f translate;
	//，本项目中设定相机的初始方向已经是正确的方向，所以并不需要进行旋转摆正相机仅作了平移，把相机放到坐标原点
	translate << 1, 0, 0, -eye_pos[0],
				0, 1, 0, -eye_pos[1],
				0, 0, 1,-eye_pos[2],
				0, 0, 0, 1;

	view = translate * view;
	return view;
}

//投影变换
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar)
//四个参数含义，eye_fov代表垂直的可视角度，aspect_ratio是宽高比，zNear和zFar分别为近远平面的z轴坐标。
{
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();//定义 4*4 单位矩阵

	Eigen::Matrix4f persp_to_ortho = Eigen::Matrix4f::Identity();//透视->正交的“挤压”矩阵”
	persp_to_ortho << zNear, 0, 0, 0,
		0, zNear, 0, 0,
		0, 0, zNear + zFar, -(zNear * zFar),
		0, 0, 1, 0;

	float half_eye_fovY = eye_fov / 2 / 180.0 * MY_PI;

//屏幕范围
	float top = -zNear * tan(half_eye_fovY);
	float bottom = -top;
	float right = aspect_ratio * top;
	float left = -right;

	Eigen::Matrix4f ortho_translate = Eigen::Matrix4f::Identity();//将方块中心移到原点
	ortho_translate << 1, 0, 0, -(right + left) / 2,
		0, 1, 0, -(top + bottom) / 2,
		0, 0, 1, -(zNear + zFar) / 2,
		0, 0, 0, 1;

	Eigen::Matrix4f ortho_scale = Eigen::Matrix4f::Identity();//将方块长宽高全变成2
	ortho_scale << 2 / (right - left), 0, 0, 0,
		0, 2 / (top - bottom), 0, 0,
		0, 0, 2 / (zNear - zFar), 0,
		0, 0, 0, 1;

	projection = ortho_scale * ortho_translate * persp_to_ortho * projection;

	return projection;
}
//实现绕任意轴旋转
Eigen::Matrix4f get_rotation(Vector3f axis, float angle)
{

    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
    Eigen::Matrix3f temp = Eigen::Matrix3f::Identity();
    float ag = angle/180*MY_PI;
    Eigen::Matrix3f tr;
    Eigen::Matrix3f mul;
    mul << 0, -axis[2], axis[1],
        axis[2], 0, -axis[0],
        -axis[1], axis[0], 0;
    tr = cos(ag)*temp + (1-cos(ag))*axis*axis.adjoint() + mul*sin(ag);
    model << tr(0,0), tr(0,1), tr(0,2), 0,
            tr(1,0), tr(1,1), tr(1,2), 0,
            tr(2,0), tr(2,1), tr(2,2), 0,
            0, 0, 0, 1;
    return model;
}



int main(int argc, const char** argv)
{
    float angle = 0;
    bool command_line = false;
    std::string filename = "output.png";

    if (argc >= 3) {
        command_line = true;
        angle = std::stof(argv[2]); // -r by default
        if (argc == 4) {
            filename = std::string(argv[3]);//将旋转某角度的图像存储到本地
        }
        else
            return 0;
    }

    rst::rasterizer r(700, 700);//确定宽高参数的屏幕

    Eigen::Vector3f eye_pos = {0, 0, 5};//相机坐标

    std::vector<Eigen::Vector3f> pos{{2, 0, -2}, {0, 2, -2}, {-2, 0, -2}};//三角形三个定点的坐标

    std::vector<Eigen::Vector3i> ind{{0, 1, 2}};//三个点的索引值

	//通过loadposition与load_indices将坐标点和索引值赋给光栅化器（rasterizer)
    auto pos_id = r.load_positions(pos);
    auto ind_id = r.load_indices(ind);

    int key = 0;
    int frame_count = 0;

    if (command_line) {
        r.clear(rst::Buffers::Color | rst::Buffers::Depth);//清屏

		r.set_model(get_model_matrix(angle));//将内部的模型矩阵作为参数传递给光栅化器。
		r.set_view(get_view_matrix(eye_pos));//将视图变换矩阵设为内部视图矩阵
		r.set_projection(get_projection_matrix(45, 1, 0.1, 50));//将内部的投影矩阵设为给定矩阵 p，并传递给光栅化器

        r.draw(pos_id, ind_id, rst::Primitive::Triangle);
        cv::Mat image(700, 700, CV_32FC3, r.frame_buffer().data());
        image.convertTo(image, CV_8UC3, 1.0f);

        cv::imwrite(filename, image);

        return 0;
    }

    while (key != 27) {
        r.clear(rst::Buffers::Color | rst::Buffers::Depth);
		//MVP变换
        r.set_model(get_model_matrix(angle));
        r.set_view(get_view_matrix(eye_pos));
        r.set_projection(get_projection_matrix(45, 1, 0.1, 50));

        r.draw(pos_id, ind_id, rst::Primitive::Triangle);//绘制三角形

        cv::Mat image(700, 700, CV_32FC3, r.frame_buffer().data());
        image.convertTo(image, CV_8UC3, 1.0f);
        cv::imshow("image", image);
        key = cv::waitKey(10);

        std::cout << "frame count: " << frame_count++ << '\n';
//控制旋转
        if (key == 'a') {
            angle += 10;
        }
        else if (key == 'd') {
            angle -= 10;
        }
    }

    return 0;
}

光栅化

屏幕由像素点构成，是离散的，二维的
最基本的二维元素是三角形，内部一定是平面

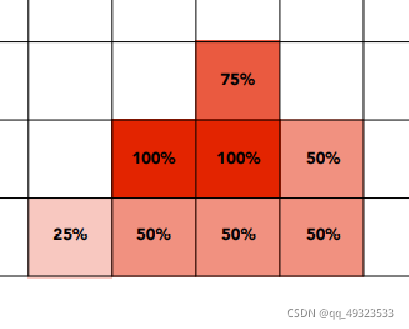
Sampling采样

寻找像素点

一个像素点对应一个坐标点，对这个坐标点采样，判断它在不在三角形里面，边界不做处理or特殊处理。

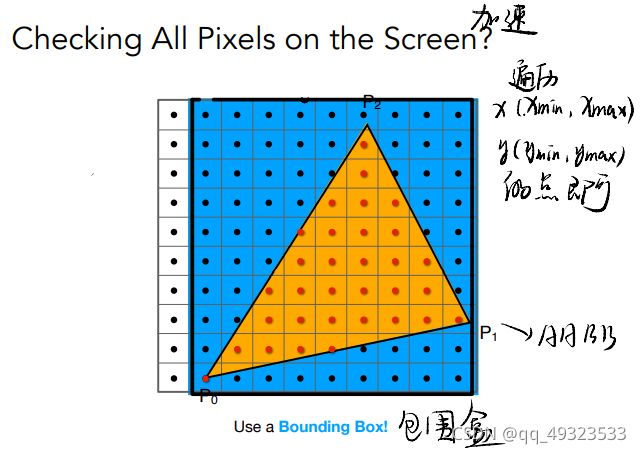
加速

方法1：直接遍历所有点浪费时间，用包围盒加速。

方法2：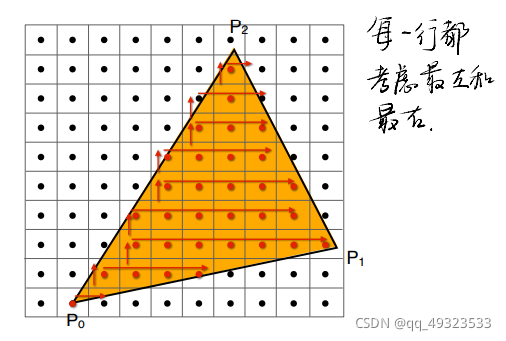

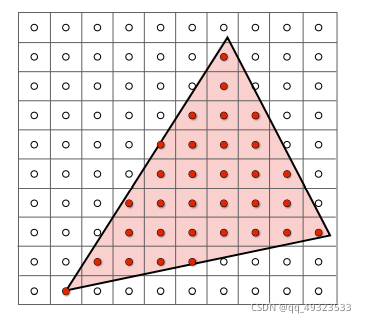
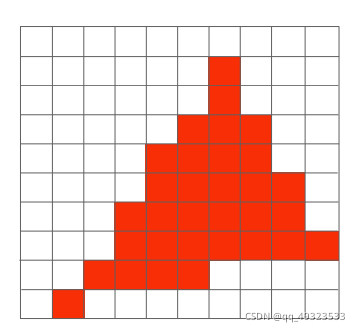
采样的缺点：以点代面，有失偏颇 → Aliasing 走样，表现为锯齿

抗锯齿

先模糊再采样

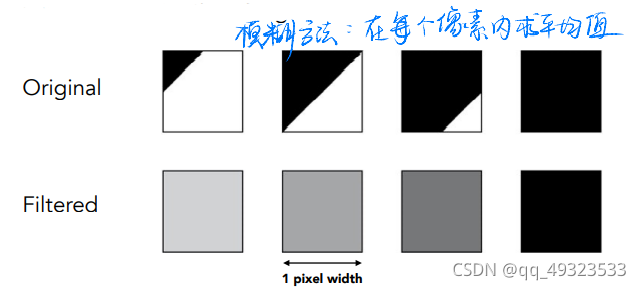
最理想的状态：像素的颜色值为负责的区域内的平均值。
但是连续域的平均值是很难求的，计算量巨大

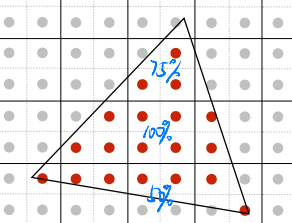
解决方法：Supersampling（MSAA）
每个像素多次采样，求平均。太浪费性能
优化：不使用均匀分布，采样复用

目前得到广泛应用的其他方法：
FXAA (Fast Approximate AA)：先获得有锯齿的图，再后处理去除锯齿（很快）

• 找到边界，换成没有锯齿的边界，（图像匹配）非常快
• 方法和采样无关，采样虽然有误，但是这种方法可以弥补

TAA (Tem‘poral AA) ：时序信息，借助前面帧的信息

• 静态场景，相邻两帧同一像素用不同的位置来sample
• 把MSAA的Sampling分布在时间上

Super resolution / super sampling 超分辨率

深度处理

绘制是有远近的，如何确定图形的绘制顺序？

1. 画家算法：由远及近画画，覆盖。无法处理互相遮挡的情况
   
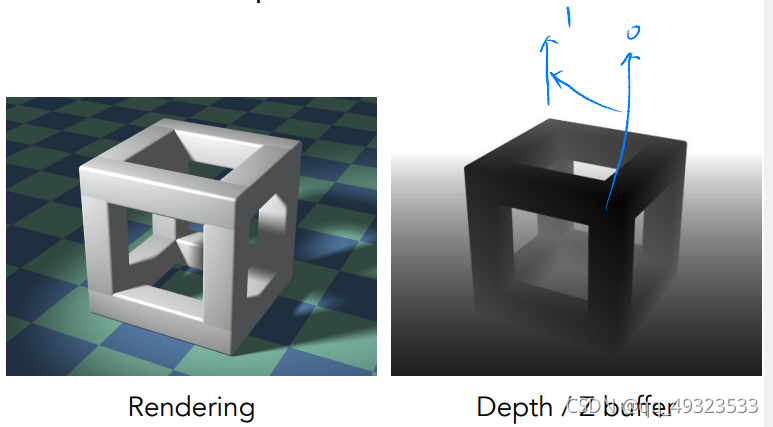
2. Z-buffer
   对每个像素多存一个深度缓冲区
   实际中，相机在原点往-z方向看，z越小说明越远
   
   
   
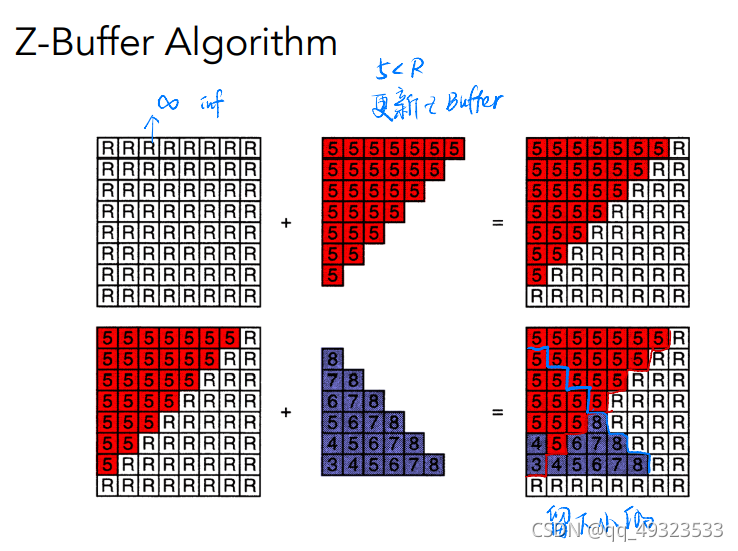
   复杂度：O(n) 并不是排序，而是只要最值
   需要保证三角形进入顺序和结果无关
   无法处理透明物体

例题

在屏幕上画出一个实心三角形，换言之，栅格化一个三角形。你需要自己填写并调用函数 rasterize_triangle(const Triangle& t)和static bool insideTriangle()

rasterize_triangle(const Triangle& t)内部工作流程如下：

1. 创建三角形的 2 维 bounding box。
2. 遍历此 bounding box 内的所有像素（使用其整数索引）。然后，使用像素中心的屏幕空间坐标来检查中心点是否在三角形内。
3. 如果在内部，则将其位置处的插值深度值 (interpolated depth value) 与深度缓冲区 (depth buffer) 中的相应值进行比较。
4. 如果当前点更靠近相机，请设置像素颜色并更新深度缓冲区 (depth buffer)。

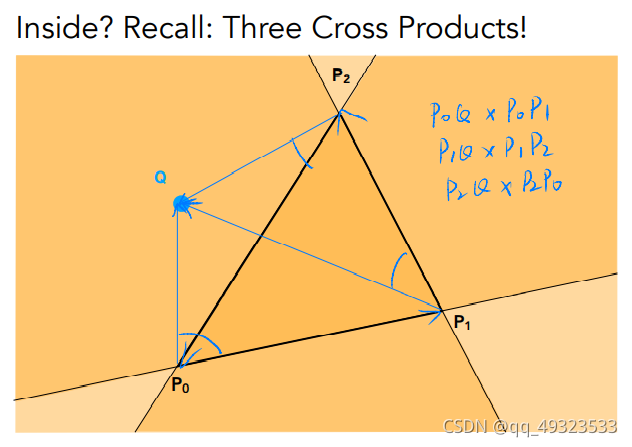
static bool insideTriangle()内部工作流程如下：

1. 三角形三边的向量
2. 测试点和三角形顶点的向量
3. 叉乘判断点在三角形内外

static bool insideTriangle(int x, int y, const Vector3f* _v)
{   
    //测试点(x,y) ， 三角形三点坐标 _v[0],_v[1],_v[2]

	//三角形各边的向量
	Eigen::Vector2f side1;
	side1<< _v[1].x() - _v[0].x(), _v[1].y() - _v[0].y();
	Eigen::Vector2f side2;
	side2 << _v[2].x() - _v[1].x(), _v[2].y() - _v[1].y();
	Eigen::Vector2f side3;
	side3 << _v[0].x() - _v[2].x(), _v[0].y() - _v[2].y();

	//测试点和三角形边界点的向量
	Eigen::Vector2f v1;
	v1 << x - _v[0].x(), y - _v[0].y();
	Eigen::Vector2f v2;
	v2 << x - _v[1].x(), y - _v[1].y();
	Eigen::Vector2f v3;
	v3 << x - _v[2].x(), y - _v[2].y();

	//三角形各边的的向量 X 测量点和三角形各点连线的向量
	//叉乘公式为(x1, y1)X(x2, y2) = x1*y2 - y1*x2
	float z1 = side1.x() * v1.y() - side1.y() * v1.x();
	float z2 = side2.x() * v2.y() - side2.y() * v2.x();
	float z3 = side3.x() * v3.y() - side3.y() * v3.x();

	//判断点在三角形 内（同号）or 外（异号）
	if ((z1 > 0 && z2 > 0 && z3 > 0) || (z1 < 0 && z2 < 0 && z3 < 0))
	{
		return true;
	}
	else
	{
		return false;
	}
}

//三角形栅格化
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
    auto v = t.toVector4();
    //v是一个包含三个顶点信息的数组，每个顶点坐标用Vector4f（齐次坐标）表示

	//构建AABB包围盒
		//找到AABB边界
	float min_x = std::min(v[0].x(), std::min(v[1].x(), v[2].x()));
	float max_x = std::max(v[0].x(), std::max(v[1].x(), v[2].x()));
	float min_y = std::min(v[0].y(), std::min(v[1].y(), v[2].y()));
	float max_y = std::max(v[0].y(), std::max(v[1].y(), v[2].y()));
    
	//遍历AABB包围盒的点
	for (int x = min_x; x <= max_x; x++) {
		for (int y = min_y; y <= max_y; y++) {
			if (insideTriangle(x, y, t.v)) {
			//判断是否在三角形内, 如果在内部，则将其位置处的插值深度值(interpolated depth value) 
			//与深度缓冲区(depth buffer) 中的相应值进行比较。
				float min_depth = FLT_MAX;//初始化无限远
				//对于三角形内部的像素，我们需要用插值的方法得到其深度值。
				auto tup = computeBarycentric2D(x,y,t.v);
				float alpha,beta,gamma;
				std::tie(alpha,beta,gamma) = tup;
				float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
				float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
				z_interpolated *= w_reciprocal;
				min_depth = std::min(min_depth, z_interpolated);

				if (depth_buf[get_index(x, y)] > min_depth) {
					//获得最上层应该渲染的颜色
					Vector3f color = t.getColor();
					Vector3f point;
					point <<x,y,min_depth;
					//更新深度
					depth_buf[get_index(x, y)] = min_depth;
					//更新所在点的颜色
					set_pixel(point, color);
				}
			}
		}
	}
}

着色

Bling-Phong Reflectance Model光照模型 着色模型

漫反射：

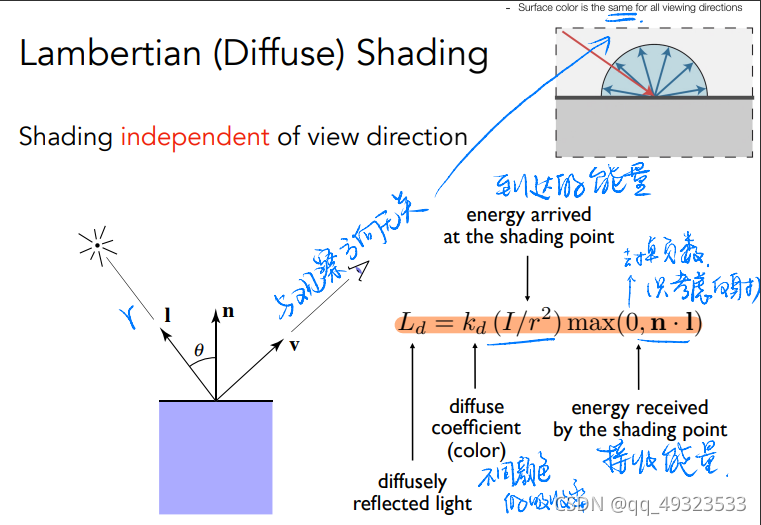
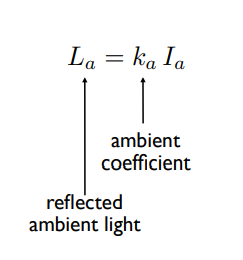
环境光：是假的，因为全局光照（GI）十分复杂，所以用环境贴图模拟

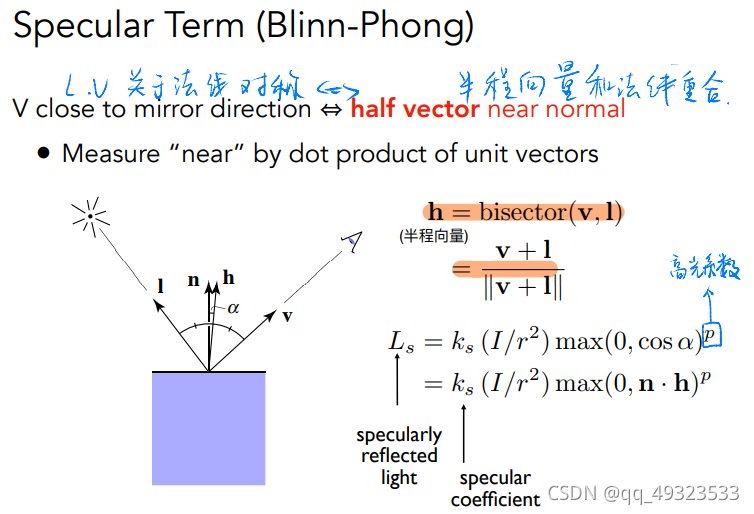
高光：

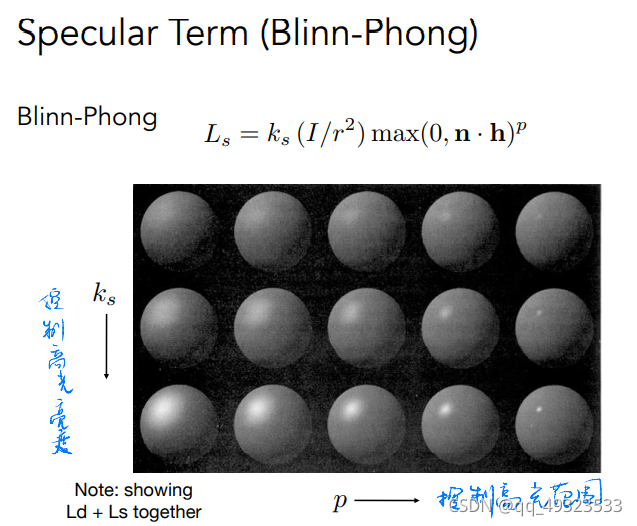
高光+漫反射+环境光 = 光照模型

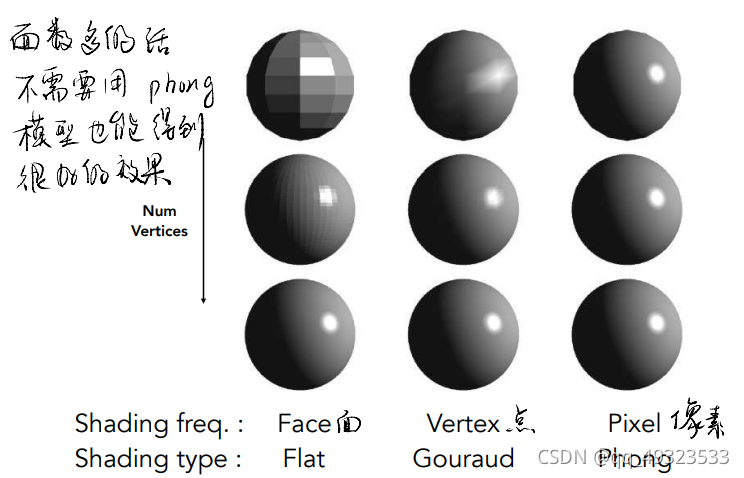
着色频率

flat shading：对每个三角形面着色

Gouraud shading：先对每个三角形的顶点着色，后对颜色插值

Phong shading：先对法线值做插值，后对每个点着色（开销大）
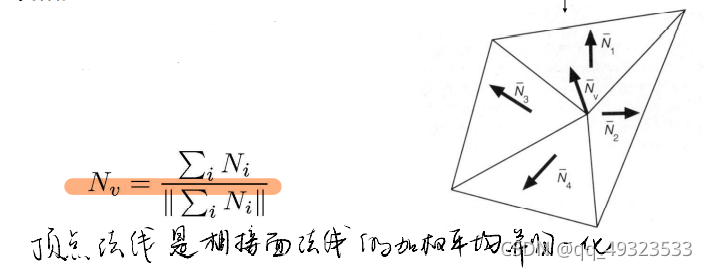
顶点法线方向的计算：相邻面的法线的平均

对比：

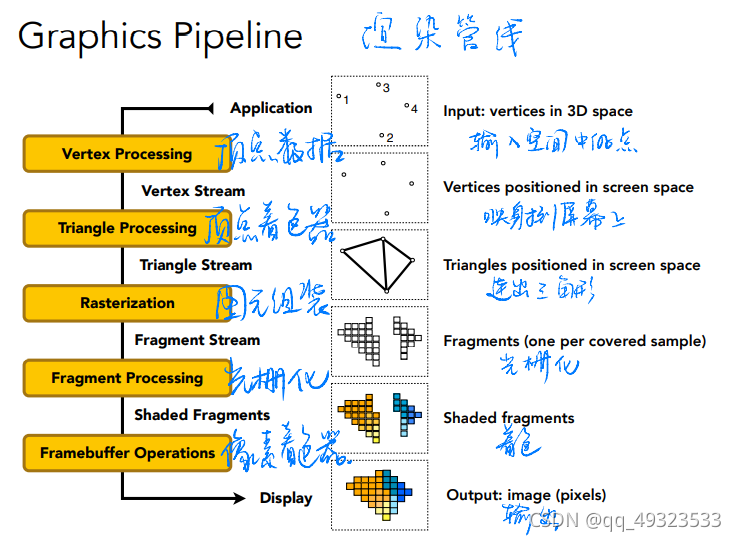
渲染管线

纹理映射

三维表面都是二维的
纹理图可映射到三维
三角形每个顶点对应一个uv坐标
一张纹理可以使用多次：纹理本身设计可以无缝衔接

三角形重心坐标

投影前后的重心坐标可能会变化，计算时需要结合深度。
所以需要在对应时间计算对应的重心坐标来做插值，不能随意复用！
计算出三角形内三个点对中心点的权重和他们对中心点的加权

应用材质：
像素在三角形内→计算对应uv→取纹理对应颜色值→设置

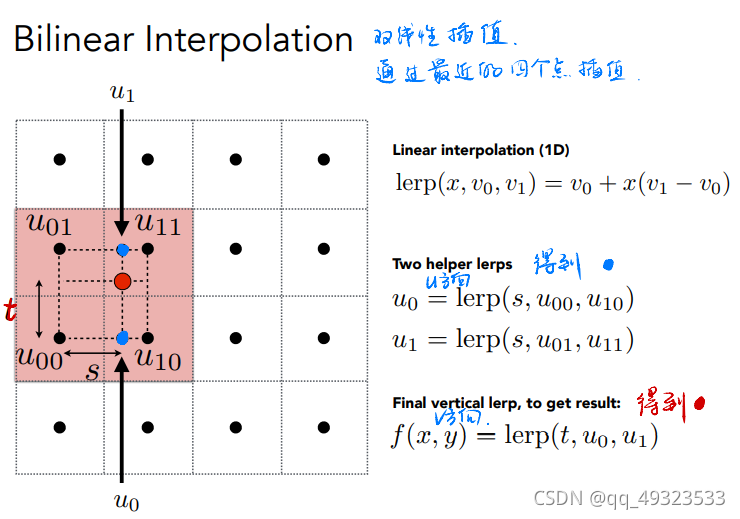
问题1：纹理过小，在大物体上被拉伸（多个像素点用一个纹素）
解决方法：双线性插值， 双向三次插值

双线性插值：

双向三次插值：周围16个点做三次插值

问题2：纹理太大，一个pixel对应了多个texel → 采样频率不足导致 摩尔纹+锯齿（走样）
解决方法：Mipmap

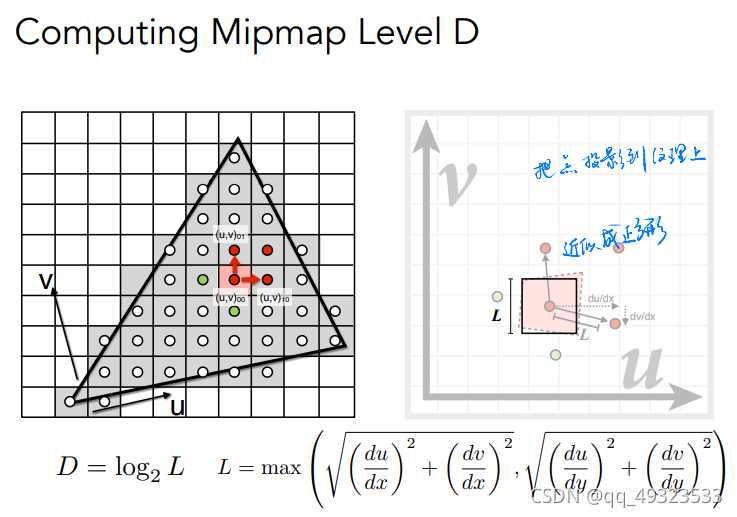
层数D约为相邻pixel的映射uv之间的距离取2的对数
若D不是整数->三线性插值

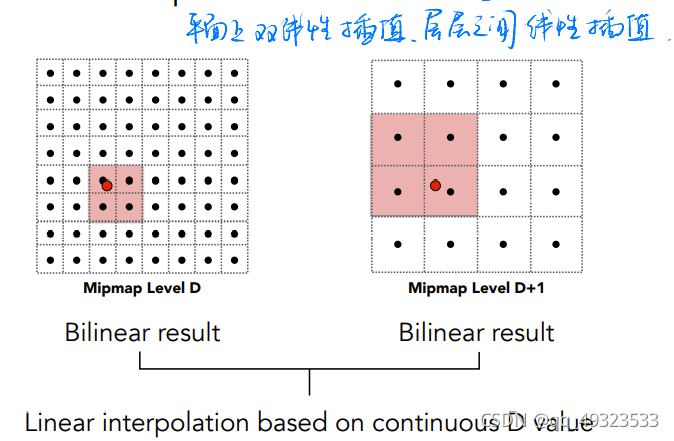
Mipmap局限性：只能正方形近似，对于某些角度、大小特别的点，处理效果不佳，产生模糊
处理方法：各向异性过滤，EWA过滤

（不太懂）

贴图

Environment Map

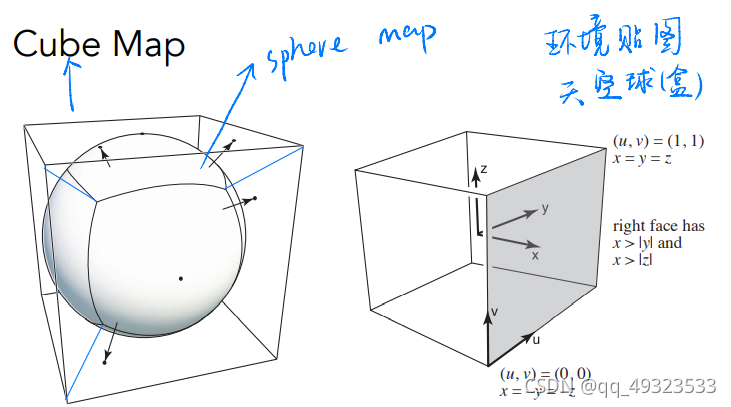
Cube Map：立方体表面，从球心到球面的投影向外

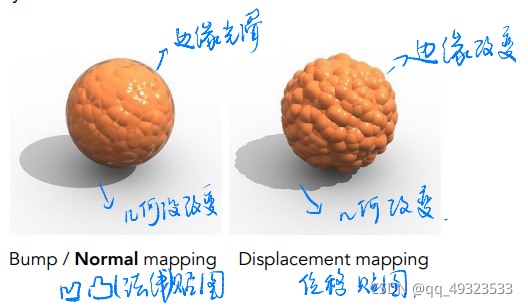
法线贴图，凹凸贴图

记录了高度移动，不改变几何信息，逐像素扰动法线方向，高度 offset 相对变化，从而改变法线方向

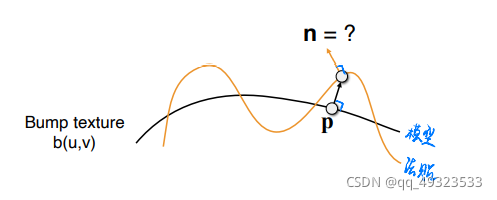
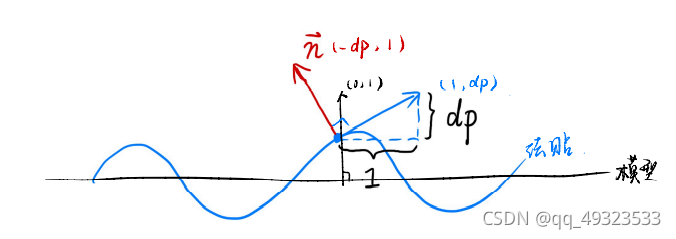
法贴扰动模型表面原理（2维）：
原来的法线：n§ = (0, 1)
扰动： dp = c * [h(p+1) - h§]
扰动后的法线： n§ = (-dp, 1)，归一化

位移贴图

改变几何信息，对顶点做位移
相比上更逼真，要求模型足够细致，运算量更高

环境光遮蔽贴图

• 计算好的环境光遮蔽贴图
• 空间换时间

过程纹理

• 定义空间中任意点的颜色
• 噪声+映射→

阴影映射

使用光栅化绘制阴影：
思想：不在阴影里的点必须同时被光线和相机看到

步骤：

1.从光源出发得到深度图→阴影贴图
2.从眼睛发出光得到标准图像(有深度)
3.将肉眼可见的点投射回光源
if 光源可见→颜色
if 阻塞→阴影

产生的问题：
走样，分辨率
只能点光源
产生的是硬阴影

例题

在代码中添加了Object Loader(用于加载三维模型), Vertex Shader 与 Fragment Shader，并且支持了纹理映射。
需要完成的任务是:

1. 修改函数 rasterize_triangle(const Triangle& t) in rasterizer.cpp: 在此处实现与作业 2 类似的插值算法，实现法向量、颜色、纹理颜色的插值。

void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos) 
{
	//构建三角形包围盒
	auto v = t.toVector4();
	int min_x = std::min({ v[0].x(), v[1].x(), v[2].x() });
	int max_x = std::max({ v[0].x(), v[1].x(), v[2].x() });
	int min_y = std::min({ v[0].y(), v[1].y(), v[2].y() });
	int max_y = std::max({ v[0].y(), v[1].y(), v[2].y() });

	for (int x = min_x; x <= max_x; x++)
	{
		for (int y = min_y; y <= max_y; y++)
		{
			if (insideTriangle((float)x + 0.5, (float)y + 0.5, t.v))
			{
				//插值
				auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
				
				//深度插值
					//如果直接进行深度插值
				//float zp = alpha * v[0].z() + beta*v[1].z()+gamma*v[2].z();
					//直接投影时三角形重心会变，所以要使用
					//透视校正插值
				float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
				float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
				zp *= Z;
				
				if (zp < depth_buf[get_index(x, y)])
				{
					//实现法向量、颜色、纹理颜色的插值
					auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);
					auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1).normalized();
					auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);
					//view_pos[]是三角形顶点在view space中的坐标,插值是为了还原在camera space中的坐标
					auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);
//payload 存储了颜色，法线，点，相机位置等等的信息
					fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
					payload.view_pos = interpolated_shadingcoords;
					auto pixel_color = fragment_shader(payload);
					//更新深度缓存，并修改像素
					depth_buf[get_index(x, y)] = zp;
					set_pixel(Eigen::Vector2i(x, y), pixel_color);

				}
			}
		}
	}
}

2. 修改函数 phong_fragment_shader() in main.cpp: 实现 Blinn-Phong 模型计算 Fragment Color.

Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);//环境光系数
    Eigen::Vector3f kd = payload.color;//漫反射系数
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);//高光系数
	//2个光源
    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};//光强
    Eigen::Vector3f eye_pos{0, 0, 10};//相机位置

    float p = 150;

    Eigen::Vector3f color = payload.color;
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    Eigen::Vector3f result_color = {0, 0, 0};
    for (auto& light : lights)
    {
	//转换成相机的相对坐标系
		Eigen::Vector3f light_dir = (light.position - point).normalized();
		Eigen::Vector3f view_dir = (eye_pos - point).normalized();
		Eigen::Vector3f half_vector = (light_dir + view_dir).normalized();

		// 距离衰减
		float r2 = (light.position - point).dot(light.position - point);

		//环境光
			//cwiseProduct()：矩阵点对点相乘
		Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);

		//漫反射
		Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r2);
		Ld *= std::max(0.0f, normal.normalized().dot(light_dir));

		//高光
		Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r2);
		Ls *= std::pow(std::max(0.0f, normal.normalized().dot(half_vector)), p);

		result_color += (La + Ld + Ls);
        
    }

    return result_color * 255.f;
}

3. 修改函数 texture_fragment_shader() in main.cpp: 在实现 Blinn-Phong的基础上，将纹理颜色视为公式中的 kd，实现 Texture Shading FragmentShader.

//纹理映射
Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload)
{
    Eigen::Vector3f return_color = {0, 0, 0};
    if (payload.texture)
    {
		return_color = payload.texture->getColor(payload.tex_coords.x(),payload.tex_coords.y());
		//phong shading的kd是从RGB中取，而texture shading的kd则是根据UV坐标从纹理中取。
    }
    Eigen::Vector3f texture_color;
    texture_color << return_color.x(), return_color.y(), return_color.z();

    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = texture_color / 255.f;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = texture_color;
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    Eigen::Vector3f result_color = {0, 0, 0};

    for (auto& light : lights)
    {
		Eigen::Vector3f light_dir = (light.position - point).normalized();
		Eigen::Vector3f view_dir = (eye_pos - point).normalized();
		Eigen::Vector3f half_vector = (light_dir + view_dir).normalized();

		// 距离衰减
		float r2 = (light.position - point).dot(light.position - point);

		//环境光
		//cwiseProduct()：矩阵点对点相乘
		Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);

		//漫反射
		Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r2);
		Ld *= std::max(0.0f, normal.normalized().dot(light_dir));

		//高光
		Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r2);
		Ls *= std::pow(std::max(0.0f, normal.normalized().dot(half_vector)), p);

		result_color += (La + Ld + Ls);
    }
    return result_color * 255.f;
}

4. 修改函数 bump_fragment_shader() in main.cpp: 在实现 Blinn-Phong 的基础上，实现 Bump mapping.

//法线贴图
Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
    
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color; 
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;


    float kh = 0.2, kn = 0.1;

	//求法线贴图的新法线
	float x = normal.x();
	float y = normal.y();
	float z = normal.z();

	Eigen::Vector3f t = Eigen::Vector3f(x * y / std::sqrt(x * x + z * z), std::sqrt(x * x + z * z), z * y / std::sqrt(x * x + z * z));
	Eigen::Vector3f b = normal.cross(t);

	Eigen::Matrix3f TBN;
	TBN <<
		t.x(), b.x(), normal.x(),
		t.y(), b.y(), normal.y(),
		t.z(), b.z(), normal.z();

	float u = payload.tex_coords.x();
	float v = payload.tex_coords.y();
	float w = payload.texture->width;
	float h = payload.texture->height;

	float dU = kh * kn * (payload.texture->getColor(u + 1.0f / w, v).norm() - payload.texture->getColor(u, v).norm());
	float dV = kh * kn * (payload.texture->getColor(u, v + 1.0f / h).norm() - payload.texture->getColor(u, v).norm());

	Eigen::Vector3f ln = Eigen::Vector3f(-dU, -dV, 1.0f);

	point += (kn * normal * payload.texture->getColor(u, v).norm());

	normal = (TBN * ln).normalized();

    Eigen::Vector3f result_color = {0, 0, 0};
    result_color = normal;

	//Bling_Phong光照
	for (auto& light : lights)
	{
		//Bling_Phong光照模型 过程
		result_color += (La + Ld + Ls);
	}
    return result_color * 255.f;
}

5. 修改函数 displacement_fragment_shader() in main.cpp: 在实现 Bump mapping 的基础上，实现 displacement mapping.

//位移贴图
Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
    
    Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
    Eigen::Vector3f kd = payload.color;
    Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);

    auto l1 = light{{20, 20, 20}, {500, 500, 500}};
    auto l2 = light{{-20, 20, 0}, {500, 500, 500}};

    std::vector<light> lights = {l1, l2};
    Eigen::Vector3f amb_light_intensity{10, 10, 10};
    Eigen::Vector3f eye_pos{0, 0, 10};

    float p = 150;

    Eigen::Vector3f color = payload.color; 
    Eigen::Vector3f point = payload.view_pos;
    Eigen::Vector3f normal = payload.normal;

    float kh = 0.2, kn = 0.1;
    
	float x = normal.x();
	float y = normal.y();
	float z = normal.z();

	Eigen::Vector3f t = Eigen::Vector3f(x * y / std::sqrt(x * x + z * z), std::sqrt(x * x + z * z), z * y / std::sqrt(x * x + z * z));
	Eigen::Vector3f b = normal.cross(t);

	Eigen::Matrix3f TBN;
	TBN <<
		t.x(), b.x(), normal.x(),
		t.y(), b.y(), normal.y(),
		t.z(), b.z(), normal.z();

	float u = payload.tex_coords.x();
	float v = payload.tex_coords.y();
	float w = payload.texture->width;
	float h = payload.texture->height;

	float dU = kh * kn * (payload.texture->getColor(u + 1.0f / w, v).norm() - payload.texture->getColor(u, v).norm());
	float dV = kh * kn * (payload.texture->getColor(u, v + 1.0f / h).norm() - payload.texture->getColor(u, v).norm());

	Eigen::Vector3f ln = Eigen::Vector3f(-dU, -dV, 1.0f);
	normal = TBN * ln;


    Eigen::Vector3f result_color = {0, 0, 0};

    for (auto& light : lights)
    {
        //Bling_Phong光照模型 过程
        result_color += (La + Ld + Ls);
    }
	result_color = normal.normalized();

    return result_color * 255.f;
}

原模型

Bling_Phong光照

材质贴图

左边是正常的材质贴图，右边是将小材质贴图拉伸后的表现，中间是小材质贴图二次插值后的模糊效果

法线贴图

位移贴图

几何&曲线/曲面

几何的表示

隐式：
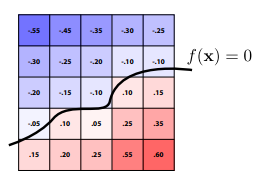
f(x)=0 , 满足该函数的所有点的集合就是几何体的边界
若带入的点 f(xi)<0,则点在面的内部，反之点在面的外部
不直观

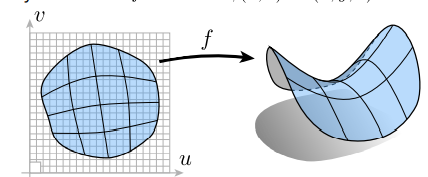
显式：
1.直接给点：所有点的集合就是面

参数映射 ：(u,v)->(x,y,z)

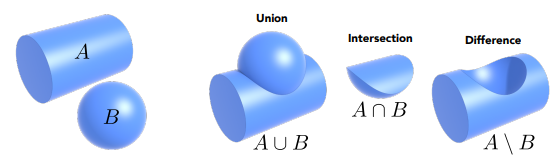
2.CSG（Constructive Solid Geometry）：基本几何体的运算

3.距离函数Distance Function

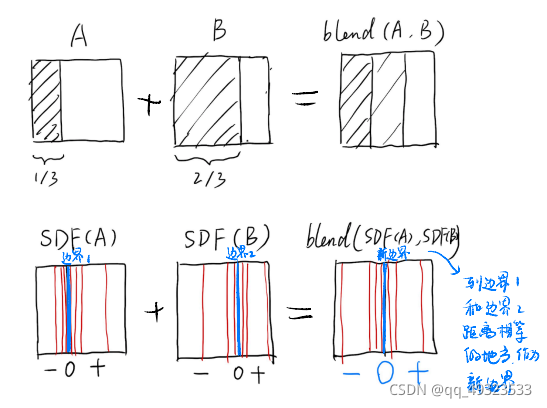
4.水平集Level Set：扫描寻找边界

5.分形：递归方法处理自相似问题

描述几何的方法

B样条延伸

基函数样条B-spline，可局部调整

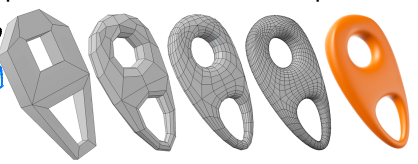
三角面

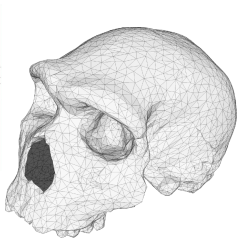
点云

贝塞尔曲面

一条由≥3个点定义的曲线：

• b0和b2定义起点和终点
• b1定义起点与终点的切线方向
• 随着时间t ，b01,b11,b02分别在b0 ~ b1，b1 ~ b2，b01 ~ b11上运动，b02走过的路径就是贝塞尔曲线。
  

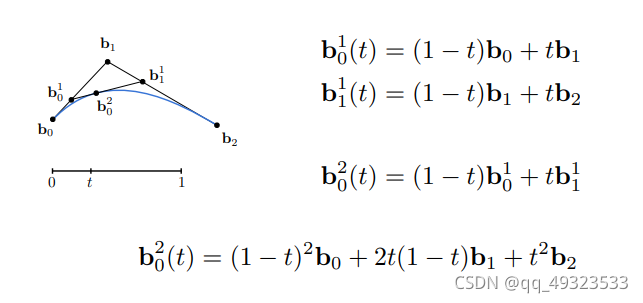
输入4个点的情况：

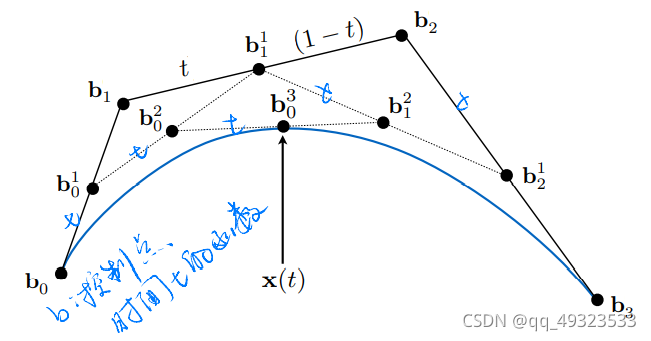
贝塞尔曲线算法：

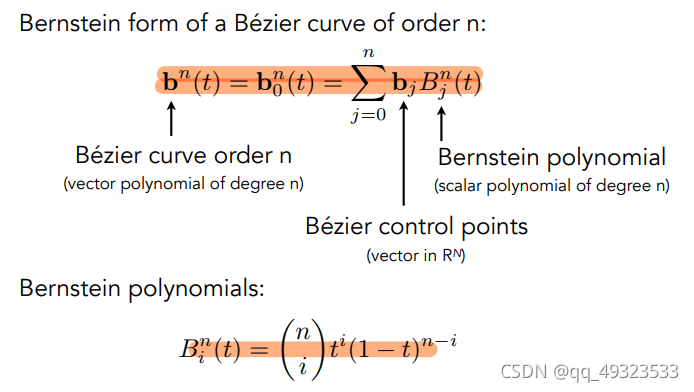
性质：
先贝塞尔后仿射 == 先仿射后贝塞尔
凸包性：曲线一定在控制点的凸包内

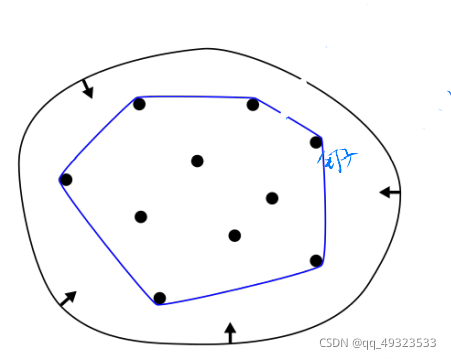
遇到的问题：高阶贝塞尔曲线（n很大），很难控制

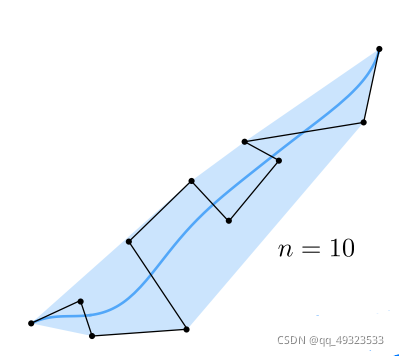
解决方法：逐段贝塞尔曲线，每四个点控制一段曲线

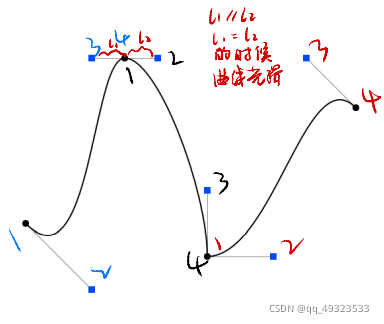
连续性保证：
前一个贝塞尔曲线的末尾控制点和后一个贝塞尔曲线的首个控制点重合

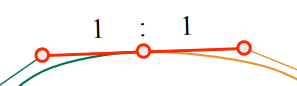
光滑性保证：
在重合的控制点的前后切线共线等长

曲面

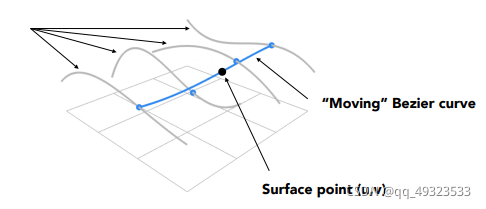
贝塞尔曲面：

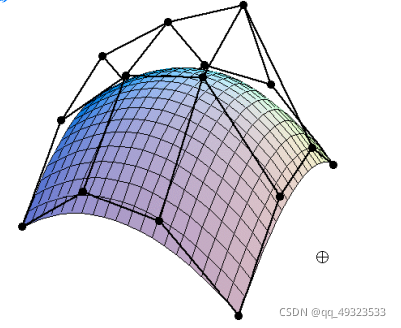
两个不同时间t（u,v）
4x4个点，四条4个控制点的贝塞尔曲线，取同一时间（比如说u）获得四个控制点，取时间v，即获得最后的曲面上的点

Mesh

曲面细分

曲面简化

曲面标准化：不会出现奇怪的三角形

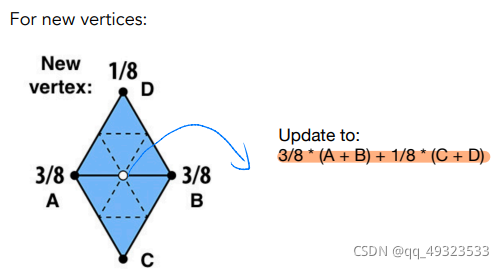
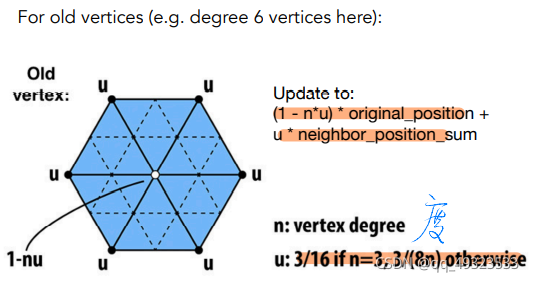
Loop细分

loop是人名，和循环无关

细分步骤：
创建更多的三角形：将每个三角形分成4个
根据 度 分别改变新点和旧点的位置

Catmull-Clark 细分

处理非四边形面，或者说奇异点（连线数!=4）