假定有这么一个需求 A是我方B是敌方,现在A需要曲线追B ,万剑归宗大家应该都见识过,这些飞剑飞向目标并不是直线它有一段曲线的过程,那这个过程是如何做到的。
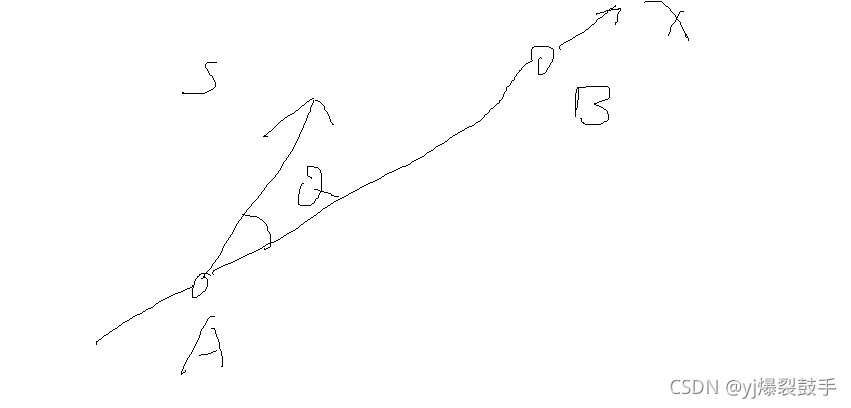
?这里s为速度方向,我们想办法推出他的公式。这个θ是相对角。因为一开始我们去配置这样一个轨迹的时候 我们粗暴的认为AB这条线就是正x轴。 不过实际游戏中AB这条轴是任意的向量,但是θ和他们的初始夹角却是一样的,如图θ是正的,这一点可以通过向量乘法去得到(向量的坐标表达式)??
我们需要得到s离不开AB 这里AB可以轻易算出来就是TargetDir,然后将TargetDir变换θ角就可以
这个变换如是 Quaternion.AngleAxis(initAngular, Vector3.forward)?
var speedDir = Quaternion.AngleAxis(initAngular, Vector3.forward) * TargetDir;
得到speedDir之后 我们自然就想到速度*时间就是位移了。当然速度大小我们是走的曲线插值(unity可以轻易做到),一般可能就是恒定的值。
但是这个速度他只是初始速度,所以我会有一个帧角度的变化我称之为angularSpeed 。
实际工程中可能会有这样的代码 相对角initAngular 的变化如下
initAngular = initAngular - tickTime * angularSpeed * mulValue;
也就是说上图θ是逐渐变小的,但其实θ是可能越界的,就是θ会变为负角度,这个时候θ就要增加了,还有θ可能会反复增加或者减小导致子弹看上去一直抖动,这就是游戏开发的乐趣所在,看到了这个问题就要解决之。我的方案如下 相对角的计算 (核心也还是2分的思想,无限去逼近0度)
if(initAngular > 0 ) //相对角大于0
? ? ? ? ? ? {
? ? ? ? ? ? ? ? int nLoopCount = 0;
? ? ? ? ? ? ? ? float mulValue = 1;
? ? ? ? ? ? ? ? var lastInitAngular = initAngular;
? ? ? ? ? ? ? ? while (nLoopCount <= 6 ) // 假如游戏帧率是30fps 0.032ms一次刷新 ?角速度是250 那么帧角速度就是
? ? ? ? ? ? ? ? //8 ,假如当前角度是0.9 那么基数8 在衰减6次之后是0.25 , 6次衰减足够精确了 精确在0.25度
? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? initAngular = initAngular - tickTime * angularSpeed * mulValue;
? ? ? ? ? ? ? ? ? ? if (lastInitAngular * initAngular < 0)
? ? ? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? ? ? initAngular = lastInitAngular;
? ? ? ? ? ? ? ? ? ? ? ? mulValue = mulValue / 2;
? ? ? ? ? ? ? ? ? ? ? ? nLoopCount = nLoopCount + 1;
? ? ? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? ? ? ? else
? ? ? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? ? ? break;
? ? ? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? ? if(nLoopCount > 6)
? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? initAngular = lastInitAngular;
? ? ? ? ? ? ? ? }
? ? ? ? ? ? }
? ? ? ? ? ? else //相对角小于0
? ? ? ? ? ? {
? ? ? ? ? ? ? ? int nLoopCount = 0;
? ? ? ? ? ? ? ? float mulValue = 1;
? ? ? ? ? ? ? ? var lastInitAngular = initAngular;
? ? ? ? ? ? ? ? while (nLoopCount <= 6)
? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? initAngular = initAngular + tickTime * angularSpeed * mulValue;
? ? ? ? ? ? ? ? ? ? if (lastInitAngular * initAngular < 0)
? ? ? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? ? ? initAngular = lastInitAngular;
? ? ? ? ? ? ? ? ? ? ? ? mulValue = mulValue / 2;
? ? ? ? ? ? ? ? ? ? ? ? nLoopCount = nLoopCount + 1;
? ? ? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? ? ? ? else
? ? ? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? ? ? break;
? ? ? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? ? if (nLoopCount > 6)
? ? ? ? ? ? ? ? {
? ? ? ? ? ? ? ? ? ? initAngular = lastInitAngular;
? ? ? ? ? ? ? ? }
? ? ? ? ? ? }