1 定义

已知向量 $\vec{a}$ 、向量 $\vec{b}$ ，则它们的叉积为 $\vec{a}$ × $\vec{b}$ 。
$\vec{a}$ 与 $\vec{b}$ 叉积得到的是一个新的向量，假设为向量 $\vec{c}$ 。
那么向量 $\vec{c}$ 同时垂直与向量 $\vec{a}$ 和向量 $\vec{b}$ ，换句话说也就是向量 $\vec{c}$ 垂直于向量 $\vec{a}$ 和向量 $\vec{b}$ 构成的平面。
叉积定义
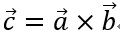
那么问题来了，向量 $\vec{c}$ 的方向和长度是多少？

1.1 叉乘的方向

一般教科书上说是根据右手定则来判定：右手平展，使大拇指与其余四指垂直，并且都跟手掌在一个平面内。将大拇指之外的其余四指与 $\vec{a}$ 的方向保持一致，然后四指转向 $\vec{b}$ 时，大拇指的方向即是 $\vec{c}$ 的方向。
但我想说的是，用右手定则来判定方向其实是不严谨的。
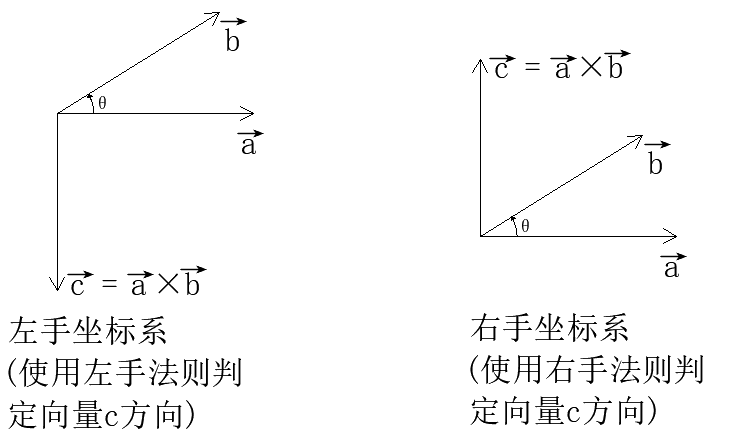
如果向量 $\vec{a}$ 和向量 $\vec{b}$ 是在左手坐标系（如Untiy中的局部坐标系、世界坐标系、屏幕坐标系）下，则应该用左手定则来判定 $\vec{c}$ 的方向。如果向量 $\vec{a}$ 和向量 $\vec{b}$ 是在右手坐标系（如Untiy中摄像机坐标系）下，则应该用右手定则来判定 $\vec{c}$ 的方向。
所以在Unity中在对世界坐标系或局部坐标系下的向量来计算叉积时，应该用左手法则来判断。
同时需要注意的是，使用Vector3.Cross求得的向量其方向也是满足左手坐标系的。
叉积的方向

1.2 叉乘的模

同时，设 $\vec{a}$ 与 $\vec{b}$ 的夹角为Θ，则有
叉积的模

2 几何意义

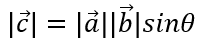
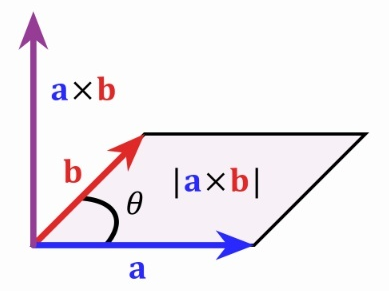
叉积的几何意义

其实就是上面定义的2点：
①向量 $\vec{c}$ 垂直于向量 $\vec{a}$ 和向量 $\vec{b}$ 构成的平面。
（这个性质用得特别多，常用来求表面的法线或者用来构建标准正交基）
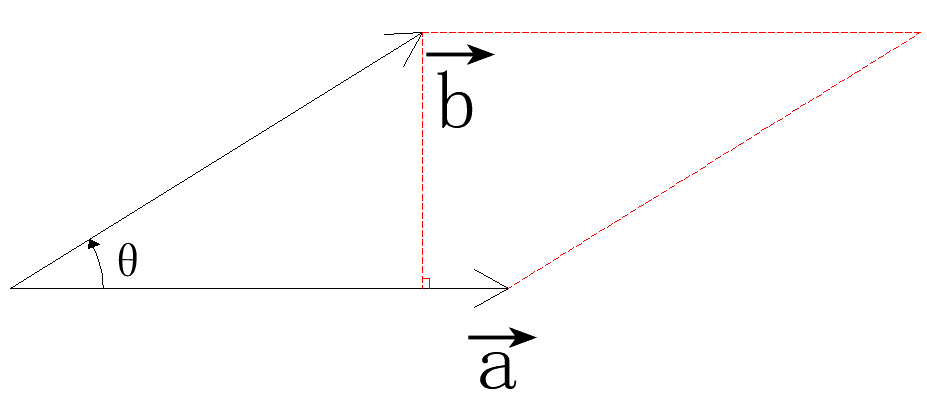
②叉乘的模其实就是向量 $\vec{a}$ 与向量 $\vec{b}$ 构成的平行四边形的面积。
叉积的模其实平行四边形的面积

3 常用公式

常用公式
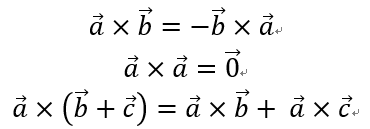
上面的分配律证明挺复杂的，这里就不多说了。
另外，设 $\vec{a}$ =(x_a，y_a， z_a)， $\vec{b}$ =(x_b，y_b， z_b)
则有 $\vec{c}$ = (y_az_b - z_ay_b，z_ax_b - x_az_b，x_ay_b - y_ax_b)
这个公式怎么来的？
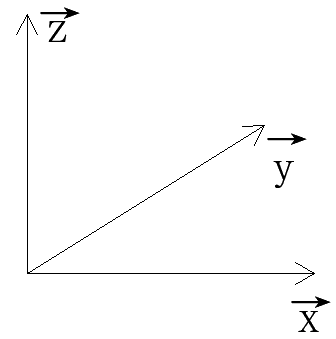
我们这里假设 $\vec{a}$ 、 $\vec{b}$ 所在坐标系的x轴、y轴、z轴的单位向量分别为 $\vec{x}$ 、 $\vec{y}$ 、 $\vec{z}$ 。同时我们假设该坐标系为左手坐标系（如Unity中的世界坐标系）。
叉乘坐标系
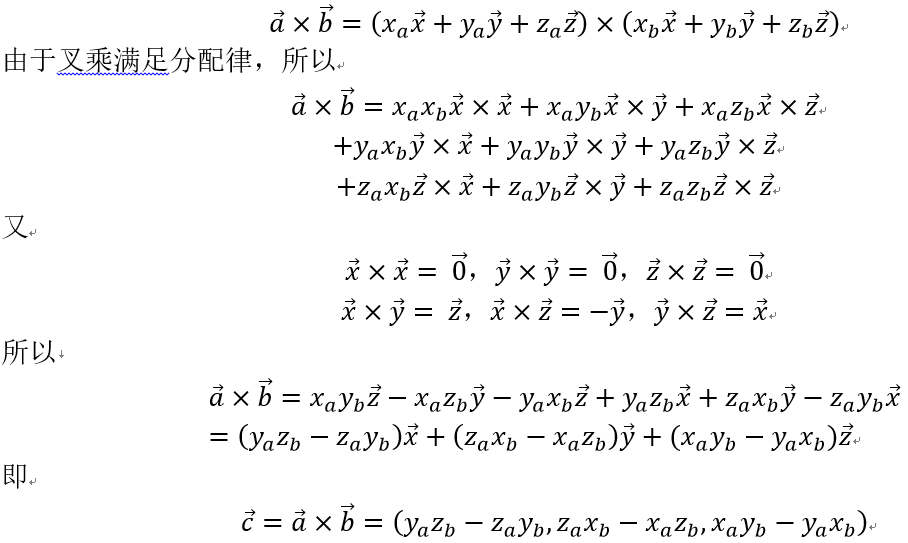
叉乘推导过程

4 应用案例

①构建坐标系
比如我们的法线贴图里面保存的法线方向其实是在切线空间下的方向。我们已知模型上局部坐标系下某一顶点的法线、切线，但我们不想用局部坐标系下的坐标来表示法线，而想一个与顶点位置无关的坐标系来表示法线，这样有什么好处呢?就是一张法线贴图可以用在不同的模型上。那么切线空间是怎么构建出来的呢？很简单，法线方向和切线方向分别为两个坐标轴，法线和切线进行叉乘得到另外一个坐标轴（这个坐标轴被称为副切线Bi-tangent，或者副法线Bi-normal）。
期限空间
②判断一个三角形是正面还是反面
比如我们已知模型上的一个三角形的三个顶点（局部坐标系），三顶点的排列顺序为顺时针ABC，如图。那么相机从上方看三角形ABC时，看到的是正面还是反面？从下方看呢？

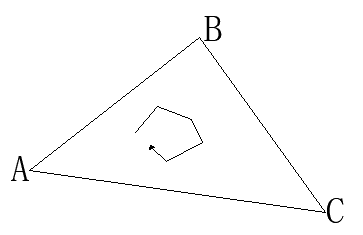
要解决这个问题，我们得先知道三角形的正面是怎么定义的。我们说，一个三角形的法线方向与相机的视线方向是相反的，那么相机看到的就是这个三角形的正面。如果一个三角形的法线方向与相机的视线方向是同向的，那么相机看到的就是这个三角形的反面。
所以核心就在于求该三角形的法线方向，法线方向该怎么求？还记得叉乘的性质吗？

向量 $\vec{c}$ (= $\vec{a}$ × $\vec{b}$ )垂直于向量 $\vec{a}$ 和向量 $\vec{b}$ 构成的平面

$\vec{AB}$ × $\vec{AC}$ 可不就是三角形ABC的法线么(注意，不能是 $\vec{AC}$ × $\vec{AB}$ 哟，因为我们上面规定ABC是顺时针排列的，如果是逆时针排列才该用 $\vec{AC}$ × $\vec{AB}$ )。
法线求到后，再求法线与视线方向的点积，若大于0，说明该三角形法线与视线方向相同，相机看到的是三角形的背面；若小于0，说明该三角形法线与视线方向相反，相机看到的是三角形的正面。