首先感谢这位大佬的系列文章
https://zzlzz.blog.csdn.net/article/details/53215105
https://blog.csdn.net/zzlyw/article/details/53217291
对投射式AR系统的基础标定做了很好的总结,并且给出了在Unity中实现对单眼位的标定方法SPAAM的实现。根据博主大佬的方法,可以成功得到针孔模型下从追踪相机坐标系到AR屏幕坐标系的变换矩阵,但这个基于针孔相机模型的矩阵并不能直接用于Unity这样的引擎中,因此在这篇文章里我会记录如何将由SPAAM算法得到的变换矩阵应用到Unity/OpenGL中,及标定后如何根据标定结果正确设置渲染相机(相对于追踪相机 AR camera)的位姿以及投影矩阵,也是自己学习的记录。
首先先回顾SPAAM的原理
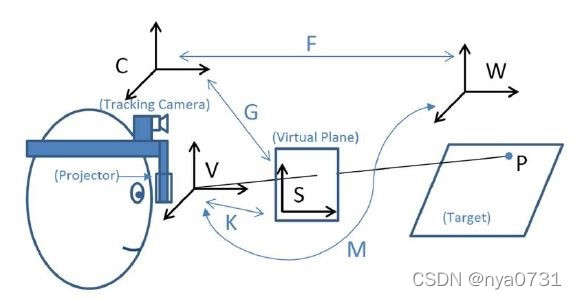

- 像手机AR之类的视频AR,由于我们是把AR内容直接渲染到摄像头拍摄的画面上,相当于摄像头就是人眼,因此上图中的人眼观测视角和追踪相机的坐标系是重合的(及坐标系C和和坐标系V重合),因此我们想要求的从坐标系C到屏幕坐标系S的变换就是从坐标系V到屏幕坐标系S的变换,而坐标系V到屏幕坐标系S的变换其实就是摄像头本身的投影变换,只要知道摄像头的内参和畸变参数就可以知道这个对应关系了。这就是为啥手机AR不需要额外的标定。
- 而对于投射式AR,坐标系C和和坐标系V重合并不重合,因此我们需要确定坐标系C和和坐标系V的相对位姿,并且需要知道“人眼这个相机”的内参。
再前面引用的博文里,我们通过借助vuforia之类的marker追踪sdk获得了一组(x,y,z)和(u,v),然后通过SPAAM对矩阵G求解和分解,就可以得到 坐标系C和和坐标系V的相对位姿R|T 以及 人眼到屏幕的内参 K,链接里博主采用了matlab实现,我是采用的github上的python版本。那么,话不多说,直接,上链接!
https://github.com/fatihksubasi/spaam
博主可以看懂,相信看博文的小伙伴也看懂咋用~~
然而这里有个小坑坑
通过RQ分解出来的内参矩阵,可能参数值本身不是正的,这可盖不住物理老师的棺材板了。虽然项目里面的有对内参的fx和fy做了强行取正,然而博主在标定的时候出现了,cx cy也不是正的情况。这样会导致算出来的相机姿态跟实际不符合,所以小伙伴记得对项目里面的spaam.py作出修改,对整个内参矩阵都强行取正
将spaam.py中139行的
K, R = self._correct_diagonal(K, R)
替换为
K = np.absolute(K)
R = np.dot(np.linalg.inv(K), self.G[:, 0:3])
然后你就能得到反应真实位姿的R|T矩阵和K啦
举个例子
spaam = SPAAM(pImage, pWorld)
G = spaam.get_camera_matrix()
K, RT = spaam.get_transformation_matrix()
R = RT[:,:-1]
T = RT[:,-1]
就可以得到旋转矩阵R,平移矩阵T,以及内参矩阵K!
那么这三个值如何转换为unity需要的呢,直接先上结论和代码!
Unity中世界到本地的旋转顺序是RzRxRy,因此由旋转矩阵到欧拉角的转换如下
def rotationMatrixToEulerAngles(R) :
### zxy
sy = math.sqrt(R[2,2] * R[2,2] + R[2,0] * R[2,0])
singular = sy < 1e-6
if not singular :
x = math.atan2(R[2,1], sy)
y = math.atan2(-R[2,0] , R[2,2])
z = math.atan2(-R[0,1], R[1,1])
else :
y = math.atan2(-R[2,0] , R[2,2])
z = math.atan2(-R[0,1], R[1,1])
z = 0
return (np.array([x, y, z])/np.pi)*180
又由于unity中
Prander = RzRxRy*(Par - T1),
(这里Rrender表示某点P在渲染相机下的坐标,Par表示点P再AR camera下的坐标)
而我们由SPAAM标定出的变换关系是
Prander = R*Par + T
因此我们最终需要赋予给渲染相机的相对旋转角为-rotationMatrixToEulerAngles?以及相对位姿为-R‘T
# 渲染相机的localRotation为
-rotationMatrixToEulerAngles(R)
# 渲染相机的localPosition为
-np.dot(R.T,T)
得到这两个值之后,在ARCamera下挂用于模拟人眼的渲染相机,将渲染相机的


或者Unity脚本中将EyeCamera的transform.localRotation和transform.localPosition分别赋值成刚才计算出的两个值就可以了。赋值方法见官方文档(https://docs.unity3d.com/2019.4/Documentation/ScriptReference/Transform-localPosition.html 和 https://docs.unity3d.com/2019.4/Documentation/ScriptReference/Transform-localRotation.html)
到这里我们完成了从R|T矩阵到Unity中相机位姿的转换,接下来是将内参矩阵K转换为Unity中需要的投影矩阵P
还是大家最喜欢的,先上结论和代码
若内参矩阵

那么相应的Unity中的投影矩阵为
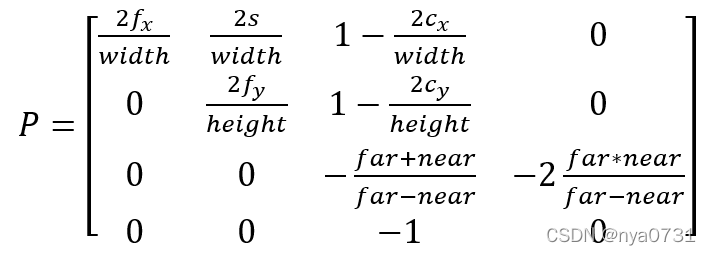
这个投影矩阵是博主自己推导的,和我之前看到的一些博文可能都不同,因为现有博文给出的大都是在不考虑内参系数s以及cx=width/2 cy=height/2情况下的,而实际标定中是不符合这两个情况的。
原理可以参考这篇博文https://zhuanlan.zhihu.com/p/440717663
但是,该博文得到的最终结果和博主推导的不一致,博主最终还是使用的自己推导出来的公式。
感兴趣的小伙伴也可以自己再推导一下,如果觉得博主的推导有问题,也欢迎交流。
def intrinsicMatrix2ProjectionMatrix(K, width, height, near_plane, far_plane):
projection_matrix = np.zeros([4,4])
fx = K[0,0]
fy = K[1,1]
sxy = K[0,1]
cx = K[0,2]
cy = K[1,2]
projection_matrix[0,0] = 2*fx/width
projection_matrix[1,0] = 0.0
projection_matrix[2,0] = 0.0
projection_matrix[3,0] = 0.0
projection_matrix[0,1] = 2*sxy/width
projection_matrix[1,1] = 2*fy/height
projection_matrix[2,1] = 0.0
projection_matrix[3,1] = 0.0
projection_matrix[0,2] = 1.0 - 2*cx/width
projection_matrix[1,2] = - 2*cy/height + 1.0
projection_matrix[2,2] = -(far_plane + near_plane)/(far_plane - near_plane)
projection_matrix[3,2] = -1.0
projection_matrix[0,3] = 0.0
projection_matrix[1,3] = 0.0
projection_matrix[2,3] = -2.0*far_plane*near_plane/(far_plane - near_plane)
projection_matrix[3,3] = 0.0
return projection_matrix
其中输入参数K就是刚才标定得到的内参K,width和height是标定时的屏幕分辨率,near_plane,和far_plane就是Unity中的near和far
将该函数计算出的projection_matrix也赋值给EyeCamera,赋值方法见Unity官方文档 https://docs.unity3d.com/ScriptReference/Camera-projectionMatrix.html
在正确赋值了 position、rotation以及 projection_matrix以后,应该就可以通过眼镜看到正确的渲染啦