前言
这一篇章我们一起来学一下three.js的几何形状。
本篇的内容比较多,因此将分为两个部分:part1和part2!
几何形状
立方体
看下文档中的案例:

我们代码实现下这个案例:
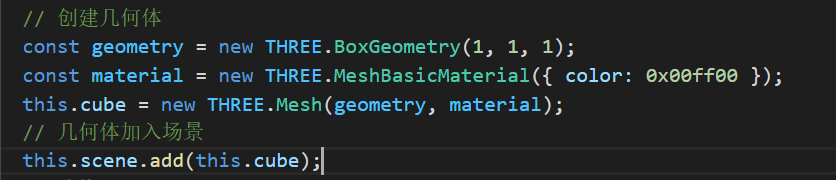
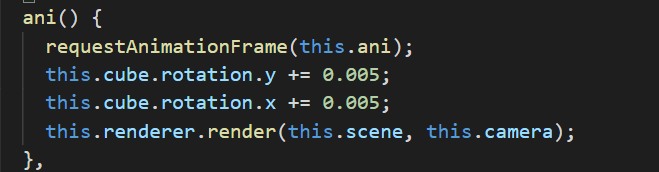
运行结果如下:

分析下这个案例:

这段代码新建一个立方体的实例,三个1表示立方体的长宽高是1!

创建一个基础材质实例,关于材质的概念我们下面的篇章再研究,这里我们根据运行的结果知道:这里材质的作用是将立方体的六个面绘制成图中的绿色。
根据字面意义再来理解记忆下:材质是组成物体的一部分,而组成物体的这一部分也会有各种各样复杂的描述(例子中就是简单的颜色描述),我们将组成物体的这一部分抽象的描述为材质!

结合代码我们知道THREE.Mesh返回的对象会被加入到场景中。
这里会有个疑惑:为什么前面创建的立方体和材质以这种方式结合起来加入场景而不是材质加入到立方体中然后直接将立方体加入到场景中?
我们来回一下第一个篇章中做的总结:加入场景的只有物体和照相机,而材质和立方体都不属于物体!

看下文档中对Mesh的介绍,Mesh表示基于xxx的物体的类。这说明它的实例对象属于物体,可以加入到场景中!暂时我们只需要了解这么多。
平面
看下文档中的案例:

代码实现的运行结果如下:

分析下这个案例:

创建一个平面实例,5表示沿着x轴的宽度,20表示沿着y轴的高度,32表示平面的宽度分段数为32。
这里我们会有个疑惑:为啥这个分段数32没有体现出来呢?
其实我们在第二个篇章提到过这个分段数,只需要给材质加一个wireframe属性就能看出效果来,如下图:
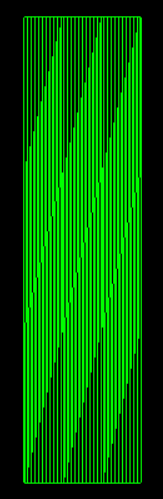

这里的材质有个side属性,我们去掉这个side看下效果:

可以看出:当长方形即将旋转到背面的时候会消失,加了这个属性后就不会。
可以得出结论:这个材质的作用可以描述为:将长方形正反两个面绘制成绿色!
球体
看下文档案例

运行结果:

看下球体的构造函数文档:

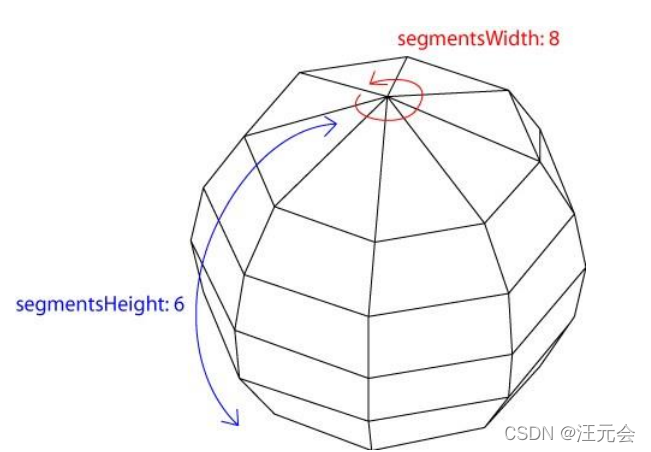
再结合这张图理解下segmentsWidth、segmentsHeight:segmentsWidth相当于经度被切成了几瓣,segmentsHeight相当于纬度被切成了几瓣,在图形底层中并没有曲线的概念,曲线是由多个折线近似构成的。所以当两个值较大的时候(曲线较多的时候)折线近似于曲线,形成的多面体也就近似于球体!
我们来用代码验证下这个结论:
这是segmentsWidth、segmentsHeight取值为6的效果:
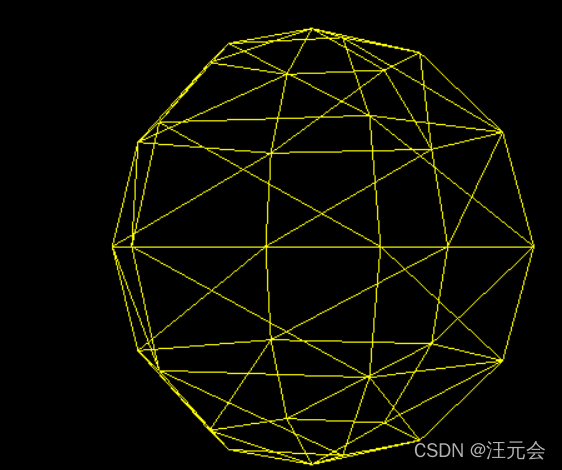
这是segmentsWidth、segmentsHeight取值为32的效果:

可以看出值越大越像一个球。
至于phiStart、phiLength,我们来演示下官方文档就知道它的作用了:
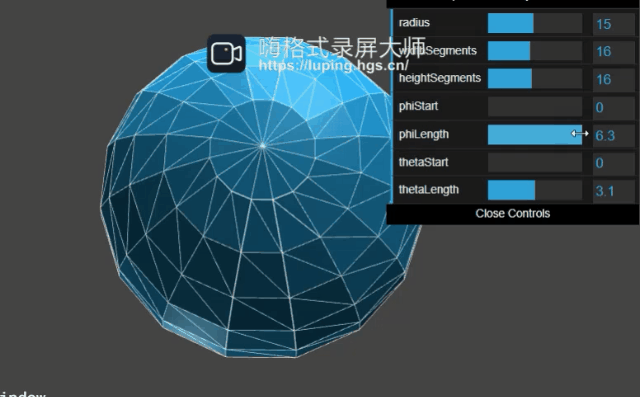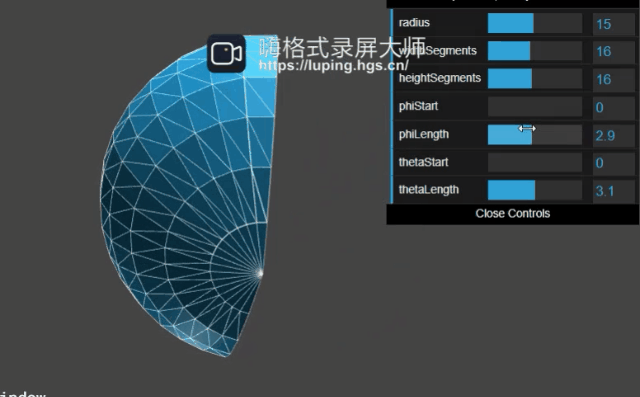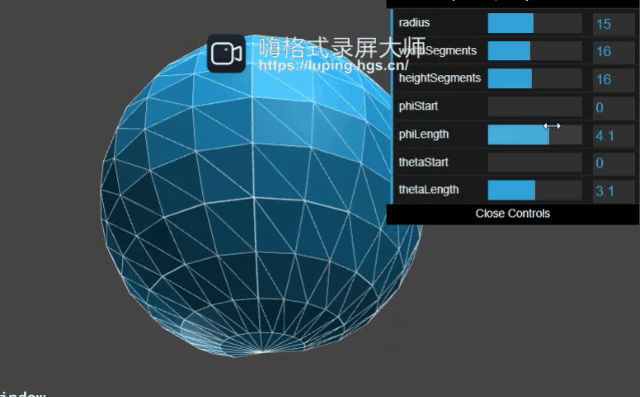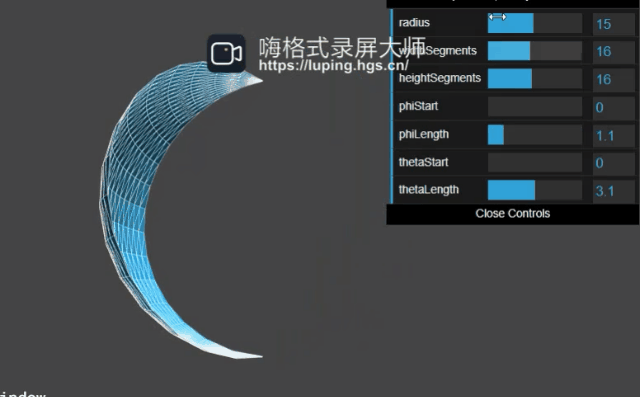
可以得出结论:phiStart,phiLength绘制了经度方向的弧形,当值为360度的时候就是球面。
同理可以得出 thetaStart,thetaLength的作用,此不作赘述。
圆形
看下案例:

运行结果如下:

看下它的构造函数:

可以发现和球体的参数类似,此不作赘述!
圆柱体
看下案例:

运行效果如下:

看下文档构造函数:

radiusTop、radiusBottom、height很好理解不作赘述,radialSegments,heightSegments我们来看下作用:
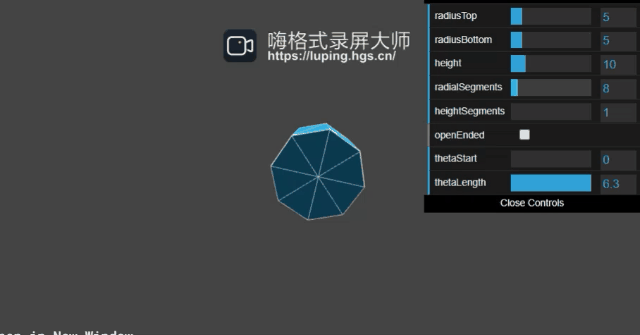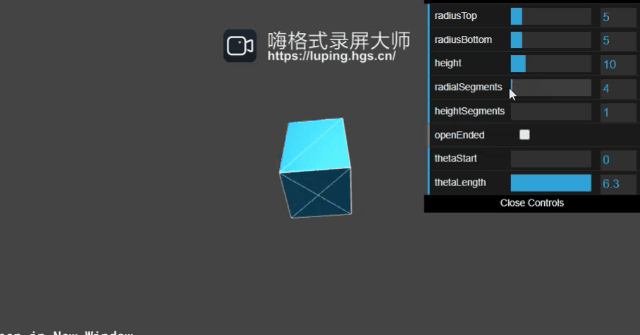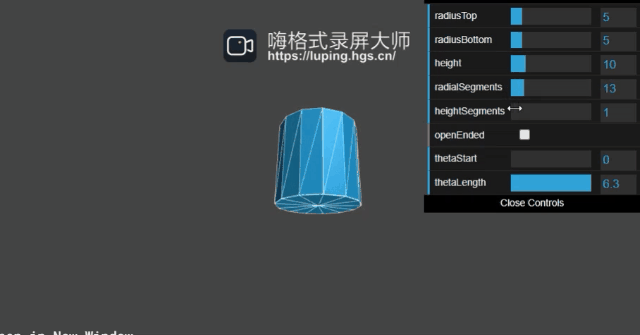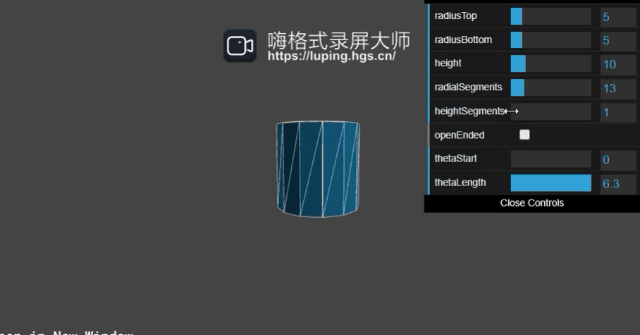
原理的话同球体的是一样的,这里也不多赘述。
thetaStart,thetaLength也是和球体一样。
openEnded作用如下:
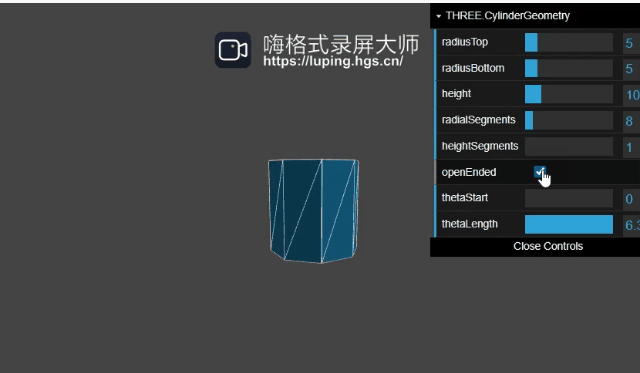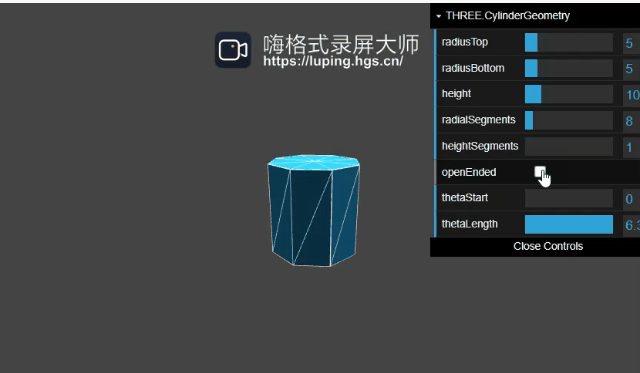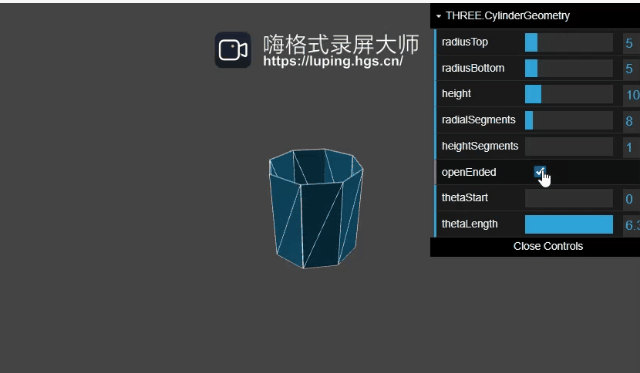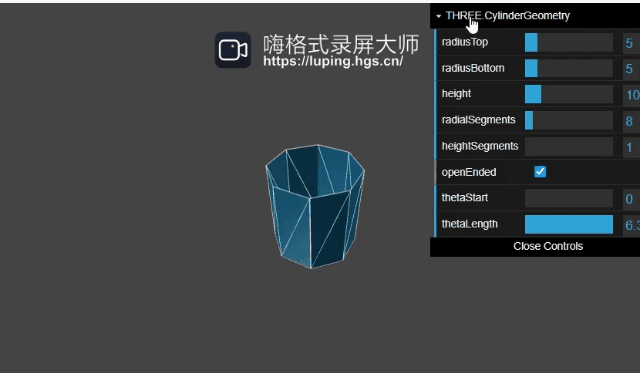
圆台
上面介绍圆柱的构造函数的时候说过:圆柱有顶部半径和底部半径,当这两者相等就是正常的圆柱,不等的话就是个圆台。
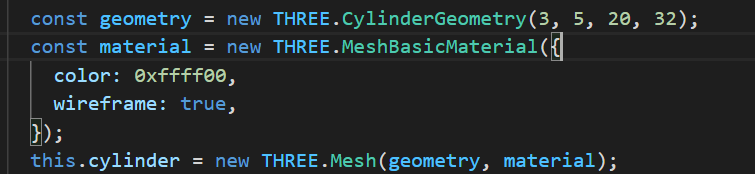
上半径设置为3,下半径设置为5的效果如下:
