一、思维导图
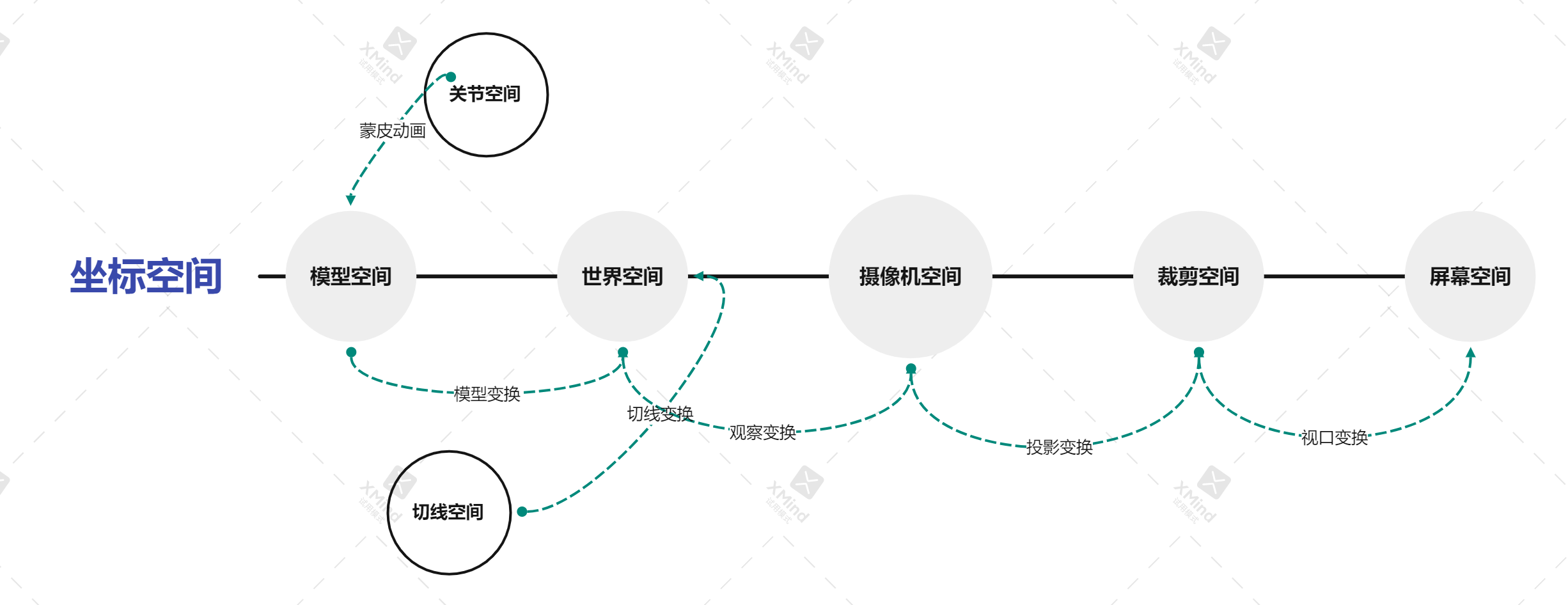
二、模型空间
这里的模型空间指的是建模出来的空间,也就是用建模软件输出的数据所在的坐标空间。比如,3D Max用的是右手系,输出的模型数据所在的空间就叫模型空间;由于Unity的模型空间是左手系,所以通常需要旋转90度才能对应上。
三、切线空间
切线空间又可以叫做纹理空间。假如纹理坐标uv构成一个二维空间,加上垂直于这个二维空间的法线,那么就是一个三维的切线空间。
3.1 法线贴图的切线空间
切线空间有什么应用了?我们在计算光照模型的时候,通常会有更精细表示法线的数据,比如法线贴图,法线贴图通常是建模软件用高模计算出来的。不过,法线贴图是原始切线空间下的数据。因此,法线贴图中的法线数据通常是(0,0,1),所以法线贴图表现出大部分是蓝色。我们在读取这个法线数据后,需要将其变换到计算光照模型所在的空间,比如世界空间。
3.2 模型空间下的切线空间
顶点上除了位置数据外,还可以有法线、切线数据。注意,这些数据都是在模型空间的。因此,法线、切线、副切线(法线和切线叉积计算出来)自然可以构成一个模型空间下的切线空间。
3.3 切线变换
假如我们想将切线空间下的法线变换到世界空间,该如何做了?我们需要得到一个世界空间下的切线空间。首先将模型空间下的切线空间变换到世界空间,这样我们就得到了一个世界空间下的切线子空间,然后用这个切线子空间构成一个切线变换,再对切线空间下的法线数据应用这个切线变换就能变换到世界空间。
用公式来表示这个变换是,
N
o
r
m
a
l
W
S
=
T
a
n
g
e
n
t
M
a
t
r
i
x
?
N
o
r
m
a
l
T
S
NormalWS=TangentMatrix*NormalTS
NormalWS=TangentMatrix?NormalTS。当然也可以将切线变换到其它的空间,比如摄像机空间,区别是构造不同的TangentMatrix。
四、关节空间
4.1 关节空间
这里的关节空间,指的是带骨骼的模型中,骨骼或者关节所定义的局部空间。
以人体手指为假设,手指会受到腕关节、肘关节、肩关节影响,对应三个骨骼。那么,手指会依次受到这三个关节的牵扯影响。我们知道,虚拟的根骨骼Root所在的是模型空间,同时每个关节也定义了自己的局部空间,比如腕关节是最终的局部空间,我们把这个关节定义的局部空间叫做关节空间。
4.2 关节姿势
所谓关节姿势,存储的是子关节到父关节的变换,包括旋转、缩放、平移,这个也可以叫做局部关节姿势。全局关节姿势是,将所有的局部关节姿势结合起来。
比如公式,
P
2
→
M
=
P
2
→
1
P
1
→
0
P
0
→
M
P_{2\to M} = P_{2\to 1} P_{1\to 0} P_{0\to M}
P2→M?=P2→1?P1→0?P0→M?表示的是将顶点从子关节2的局部空间变换到模型空间。全局关节姿势可以表示为
P
j
→
M
=
∏
i
=
j
0
P
i
→
p
(
i
)
P_{j\to M} = \prod _{i=j}^{0} P_{i\to p(i)}
Pj→M?=∏i=j0?Pi→p(i)?,其中p(i)是关节i的父关节。
4.3 绑定关节姿势
我们知道,默认情况下,蒙皮骨骼都有一个T-Pose,即绑定姿势,也可以理解为初始姿势。模型空间的顶点乘以绑定姿势的逆变换就能得到关节空间的顶点。
4.4 蒙皮矩阵
模型空间的顶点乘以绑定姿势的逆变换就能得到关节空间的顶点。关键点来了,这个时候再乘以骨骼的当前全局姿势矩阵,就又变换回了模型空间。所谓的蒙皮矩阵,就是这两个变换的结合。可以用公式表示骨骼i的蒙皮矩阵, K j = ( B j → M ) ? 1 C j → M K_{j} = (B_{j\to M})^{-1} C_{j \to M} Kj?=(Bj→M?)?1Cj→M?,B代表绑定姿势,C代表当前姿势。多个蒙皮矩阵的加权,就能得到蒙皮动画。
4.5 蒙皮动画
顶点会受到多个骨骼影响,这些骨骼的影响加权和为1,这个就是蒙皮动画。可以用公式来表示, p ′ = ∑ i = 1 n W i ( p ) K i p p' = \sum_{i=1}^{n}W_i(p)K_ip p′=∑i=1n?Wi?(p)Ki?p。其中,p是模型空间的顶点,Wi是骨骼i影响的权重,Ki是骨骼i的蒙皮矩阵。蒙皮矩阵的计算如上所示。
4.6 总结
根据以上五步的推导,蒙皮动画需要存储的数据是,
- 绑定姿势下的的模型空间顶点
- 绑定关节姿势的逆矩阵
- 当前姿势数据(实时计算当前姿势矩阵)
- 蒙皮矩阵的权重
五、世界空间
所谓世界空间,不需要解释了吧。放在游戏场景里面,指的是规定了场景坐标系的空间。模型空间,则指的是场景内的单个模型自身数据所在的空间。
5.1 模型变换
模型变换就是将模型空间的顶点数据变换到世界空间,通常包括对模型的平移、旋转和缩放。但是,一般要求的变换顺序是先缩放、再旋转、最后平移,如果反过来会造成平移受到前面的变换影响,与直观印象不符合。
所以,KaTeX parse error: Undefined control sequence: \* at position 28: …TranslateMatrix\?*?RotateMatrix\*S…。特别说明平移矩阵指的是,将模型从原点移动到其在世界空间的位置。
六、摄像机空间
摄像机空间也叫做观察空间。摄像机可以理解为世界空间的一个位置和朝向,比如在坐标(1,1,1)看向原点,那么射线的位置就是坐标(1,1,1),前向就是看向的方向(-1,-1,-1)。这个时候再定义一个垂直于forward的Up方向,就可以根据叉积找到垂直forward和up方向的right方向。这三个方向就可以构成一个摄像机空间。
6.1 观察变换
观察变换是将顶点从世界空间变换到新的摄像机空间。首先,需要将顶点平移,比如上述情况下的原点在观察空间下是(-1,-1,-1);然后,需要旋转顶点以匹配观察空间的坐标轴。由于观察空间的坐标轴是世界空间下的单位正交基,因此将三个轴放入矩阵即可得到旋转矩阵的逆矩阵(等于旋转矩阵的转置矩阵)。
七、裁剪空间
裁剪空间指的是观察空间下的顶点经过投影变换后所处的空间。我们知道,可视区域是摄像机前面的一个平截头体(透视投影)或者一个长方体(正交投影)。裁剪空间的用途是将可视区域外的物体裁剪,同时计算物体的二维坐标。
7.1 投影变换
投影分为透视投影和正交投影两种,透视投影会造成近大远小的效果,符合视觉效应,三维游戏一般使用透视投影,正交投影则远近一样大,通常只用于建模软件。
透视投影
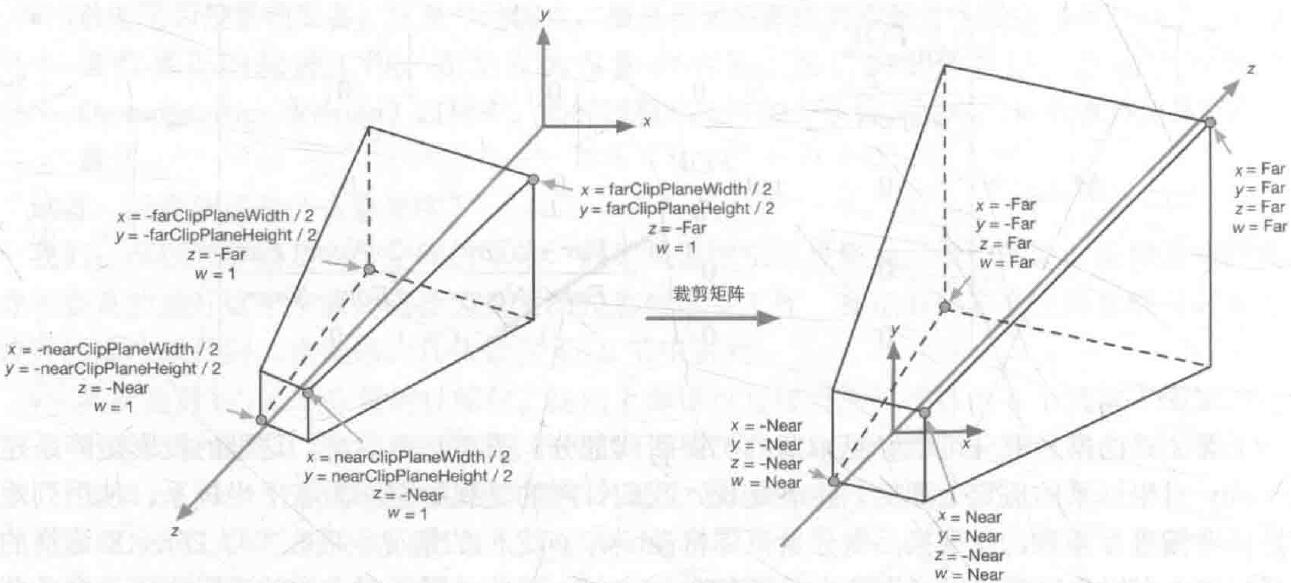
从图可以看出,透视投影后w是有值的,并不是1,结果还是一个平截头体。具体的矩阵推动,请参考相关资料。
正交投影
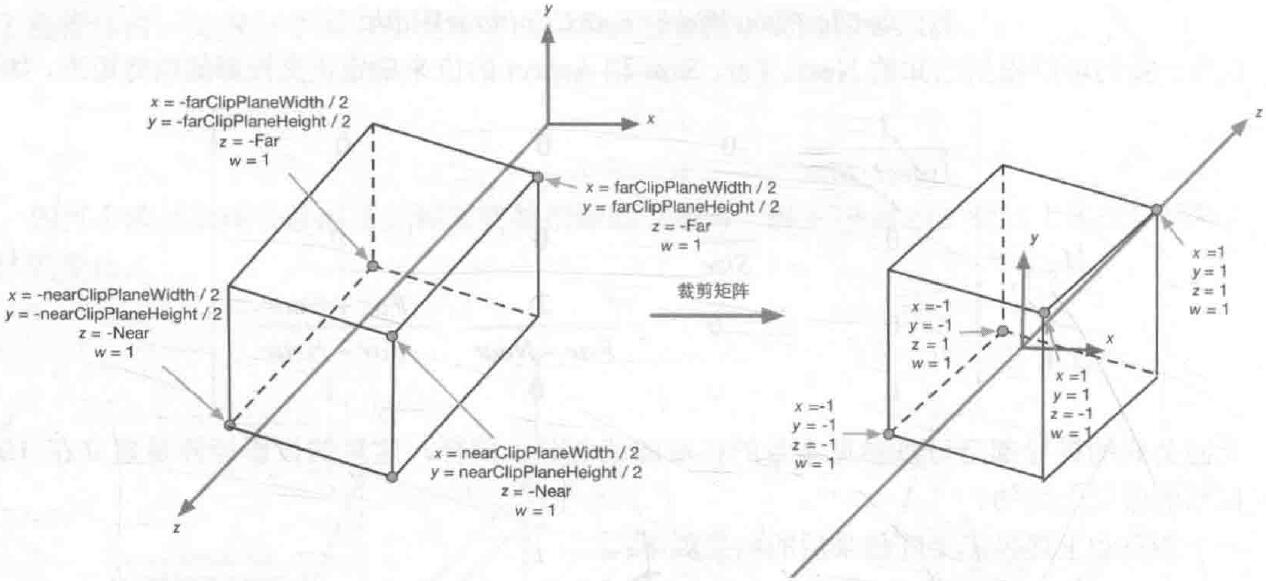
从图可以看出,正交投影实际上就是缩放和平移的结合,得到的结果是一个-1到1范围的立方体。
7.2 透视除法和图元裁剪
由于透视投影后齐次坐标的w非1,需要进行透视除法,这个是图形硬件自动进行的。如图所示:
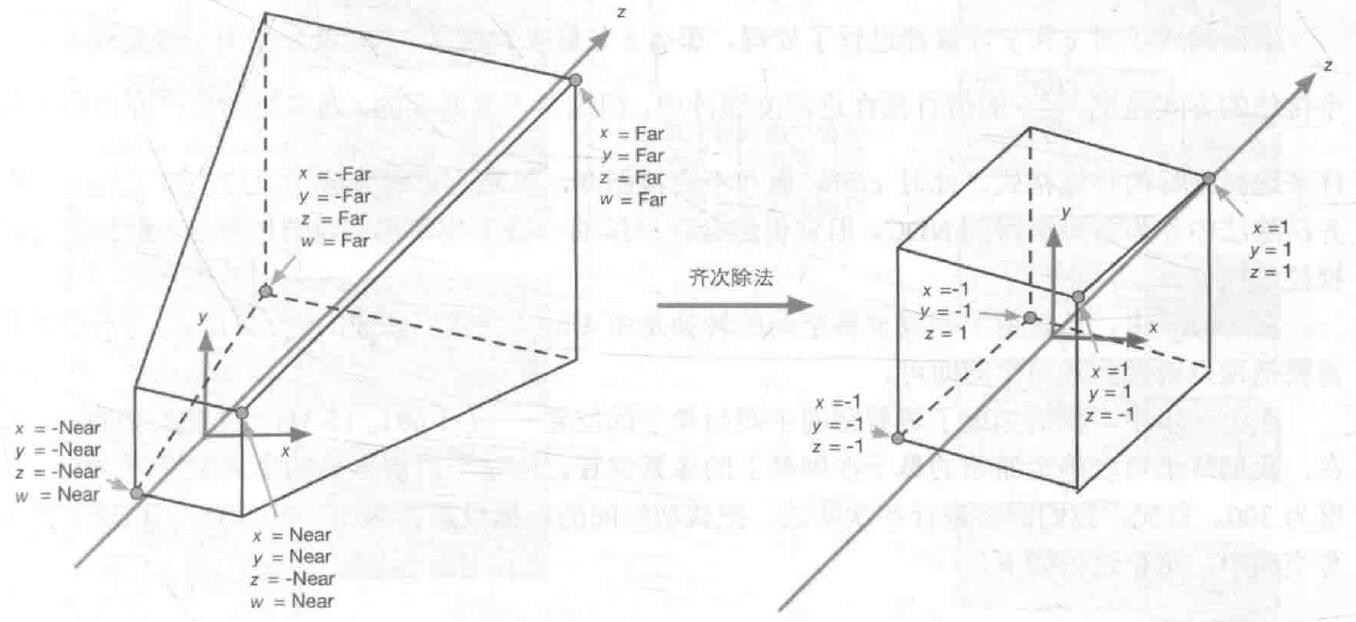
透视除法后,可以得到和正交投影结果一样的规范化立方体,也叫做NDC(规范化设备坐标系)。
到了NDC后,就可以方便的进行图元裁剪,毕竟坐标都是-1到1了(DirectX下Z坐标是0到1)。
7.3 顶点着色器的输出
顶点着色器必须输出裁剪空间下的坐标。由于DirectX的NDC的Z范围是0到1,与OpenGL的-1到1有一定区别。因此,这2者的投影矩阵在Z坐标上有一定的平移和缩放区别。
八、屏幕空间
投影变换后得到的顶点范围是-1到1。现在还需要将NDC下的顶点映射到屏幕空间。屏幕空间也可以叫做窗口空间,即窗口定义的坐标空间。
8.1 视口变换
假设,窗口坐标原点在左下角(OpenGL的原点在左下角,但是DirectX的在左上角),窗口大小为Width和Height。视口变换就是把-1到1的x和y坐标范围映射到(0,width)和(0,height),对应DirectX的话,y还需要取反。这就是一个平移和缩放的过程。
实际上,透视除法和视口变换(屏幕空间映射)都是硬件自动进行的。