[游戏开发] Unity 柏林噪声

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 游戏开发 -> Unity 柏林噪声 -> 正文阅读

[游戏开发]Unity 柏林噪声

关于柏林噪声：

先粘贴关于百度百科的一段话：

柏林噪声 (Perlin noise )指由Ken Perlin发明的自然噪声生成算法。一个噪声函数基本上是一个种子随机发生器。它需要一个整数作为参数，然后根据这个参数返回一个随机数。如果两次都传同一个参数进来，它就会产生两次相同的数。这条规律非常重要，否则柏林函数只是生成一堆垃圾

但是百度百科中没有更多关于柏林噪声具体实现的步骤过程，而在维基百科有介绍到柏林噪声生成的大概的步骤：
在这里插入图片描述

整个过程简要的分为三部分：

选取随机点，给定随机值
给定点位的梯度（用插值函数标识）
根据随机点的值与梯度计算出为赋值位置的数值

在这一过程中Perlin Noise使用一些特殊的处理策略保证生成的数据伪随机并且连续

简单演绎一维柏林噪声：

根据维基百科的步骤叙述，来演绎一下一维柏林噪声的创建过程：

首先创建一个坐标系，以X轴作为一维坐标参考点位，Y轴作为以为坐标的参考值，这样就创建了一个基本的坐标系

先在一个一维数组上选择一些位置，为他们随机的赋值，而在这些点位中间的位置，就需要通过一些插值算法来获取到值，最终获取到一条连续的曲线

在上面的过程中，有几个关键的点：

如何选择赋值的位置
如何对其进行赋值
采用哪种插值方式获取非整数点的数值

在一维的噪声生成案例中，我们可以根据X坐标轴来间隔取整获取这些点位，然后通过随机方法来为这些整数点赋值。接下来就可以在非整数点通过相邻的两个整数的数值插值计算出其对应的值，这样就可以得到一条连续的曲线，也就是一维的柏林噪声图，简单的写一个代码画出一个坐标轴，并基于Line Renderer绘制一维柏林噪声：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class PerlinNoise : MonoBehaviour
{
    public int lineWight;

    //public List<Vector3> points;
    public GameObject posPre;
    public Dictionary<int, Vector3> points = new Dictionary<int, Vector3>();
    public LineRenderer line;

    public int interIndexMax = 100;

    private void Awake()
    {
        CreatePos();
        CreateLine();
    }
    //画出整数点对应数值点位
    void CreatePos()
    {
        for (int i = 0; i < lineWight; i++)
        {
            float num = Random.Range(0f, 4f);

            Vector3 pointPos = new Vector3(i, num, 0);
            GameObject go = Instantiate(posPre, this.transform);
            go.transform.position = pointPos;
            points.Add(i, pointPos);
        }
    }
    //相邻两个整数点位之间插值获取其他位置数值
    void CreateLine()
    {
        int posIndex = 0;
        int interIndex;
        line.positionCount= interIndexMax * (points.Count - 1);
       	for (int i = 1; i < points.Count; i++)
        {
            interIndex = 0;
            while (interIndex< interIndexMax)
            {
                interIndex++;
                float posY = points[i - 1].y + (points[i].y - points[i - 1].y) * (interIndex / (float)interIndexMax);
                Vector3 pos = new Vector3(i - 1 + interIndex / (float)interIndexMax, posY, 0);
                line.SetPosition(posIndex, pos);
                posIndex++;
            }
        }
    }

在上面的代码中，可以看出，相邻的两个整数点之间会进行一次线性插值，来求出两点之间的具体曲线，运行代码后可以看到下面的效果：

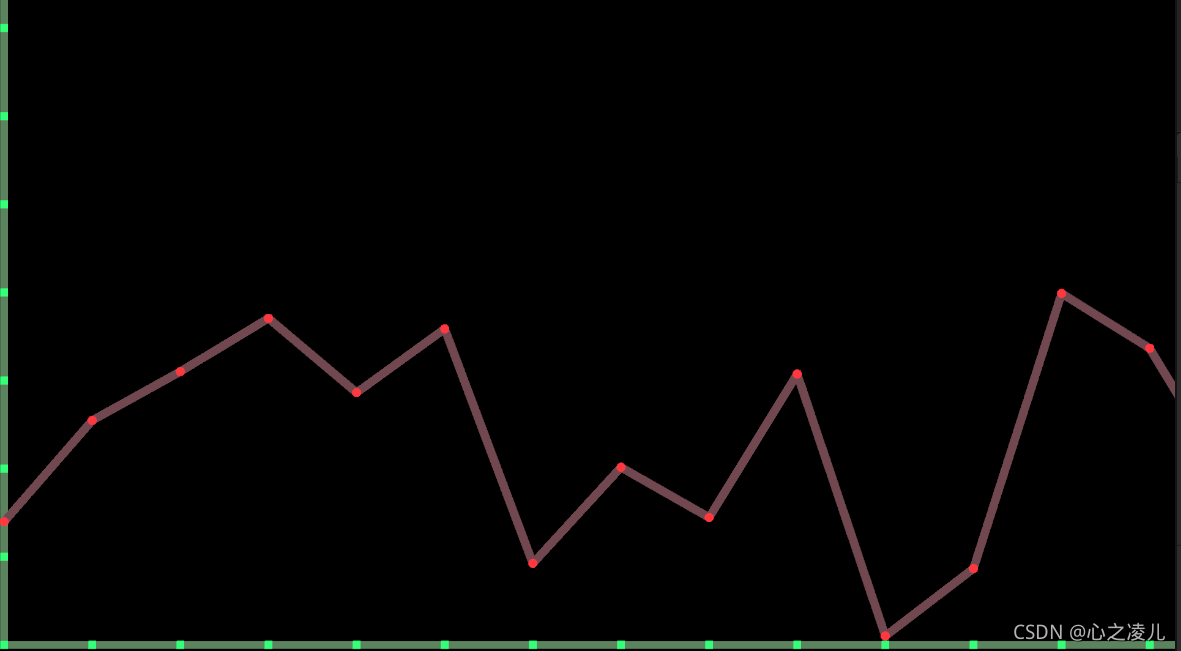
在这里插入图片描述

在上面的一维柏林噪声生成中，我们基于线性插值获取到了一条连续的折线，由于程序会在相邻两个整数点之间进行一次线性插值获取到中间点的坐标。结果得到一条直线，同时在一个整数点的左右两边使用了不同的插值区间，结果使得两边的曲线在整数点的斜率不同，最终造成了Perlin Noise生成的一维曲线在整数点的不连续

为了避免上面的情况，使得得到的Perlin Noise更加平滑自然，Ken Perlin建议使用： $3t^{2}-2t^{3}$ 作为Perline Noise的插值函数，而在最新版本算法该插值函数又被更换为 $6t^{5}-15t^{4}+10t^{3}$

为了更好理解这两个插值函数，先通过可视化代码看一下生成的曲线效果，首先是 $3t^{2}-2t^{3}$ 插值函数的显示效果，我们简单的修改一下求插值方法，更新画线插值处的代码：

 	//相邻两个整数点位之间插值获取其他位置数值
    void CreateLine()
    {
        int posIndex = 0;
        int interIndex;
        line.positionCount = interIndexMax * (points.Count - 1);
        for (int i = 1; i < points.Count; i++)
        {
            interIndex = 0;
            while (interIndex< interIndexMax)
            {
            	interIndex++;
                float posY = Mathf.Lerp(points[i - 1].y, points[i].y, InterpolationCalculation(interIndex / (float)interIndexMax));
                Vector3 pos = new Vector3(i - 1 + interIndex / (float)interIndexMax, posY, 0);
                line.SetPosition(posIndex, pos);
                posIndex++;
            }
        }
    }

    //插值函数的计算
    float InterpolationCalculation(float num)
    {
        return 3*Mathf.Pow(num, 2)-2*Mathf.Pow(num,3);
    }

在上面的代码中，简单的封装了一个函数计算公式，然后通过线性插值做了一个从两个整数点的区间范围到（0，1）之间的映射，最终得到的曲线为：
在这里插入图片描述

与线性插值，整条曲线明显平滑了许多，并且由于插值函数 $3t^{2}-2t^{3}$ 在x取值0和1时对应的坐标点斜率为0，所以最终求得的插值曲线在整数点呈连续状态, 但是在整数点看起来依旧尖锐，所以在最新Perlin Noise生成算法中插值函数被更换为 $6t^{5}-15t^{4}+10t^{3}$ ，下图是两个曲线插值函数得到的噪声曲线对比：

蓝色曲线：代表 $6t^{5}-15t^{4}+10t^{3}$ 获取的噪声曲线
红色曲线：代表 $3t^{2}-2t^{3}$ 获取的噪声曲线

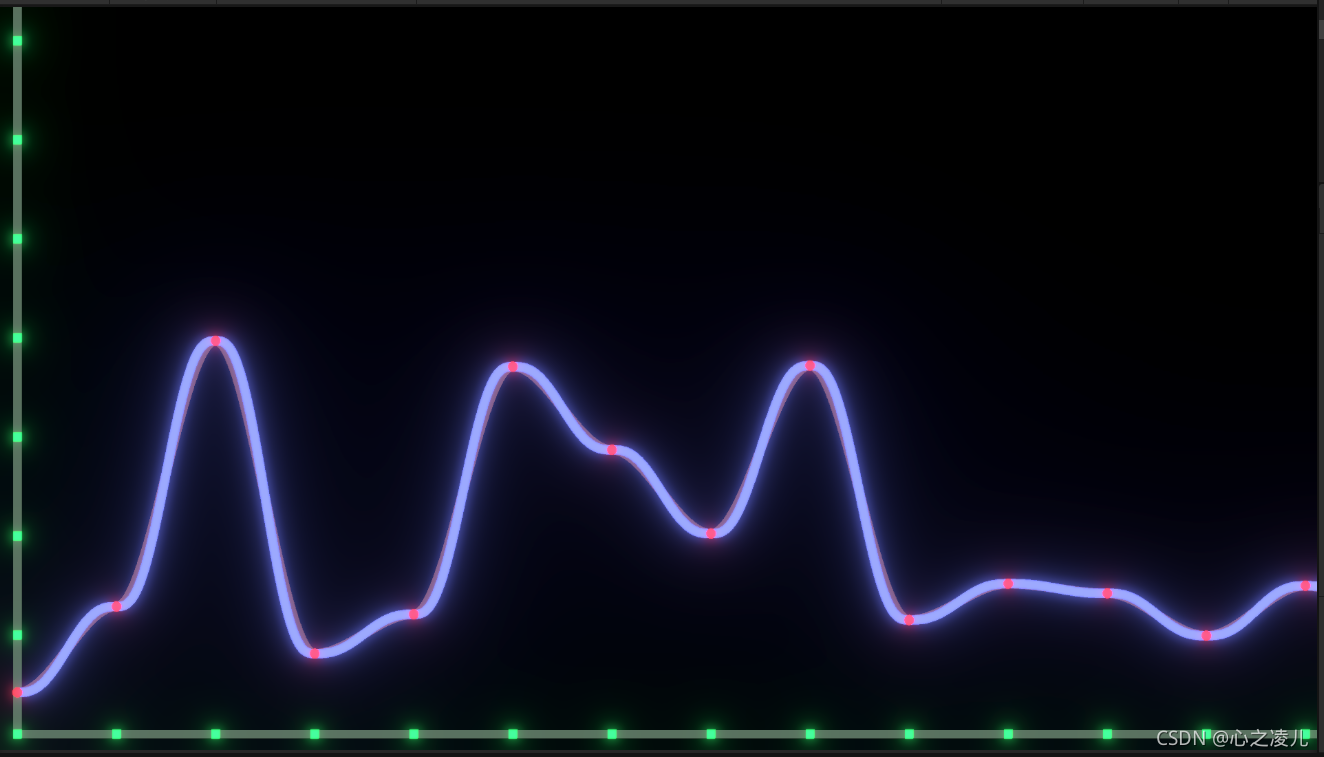
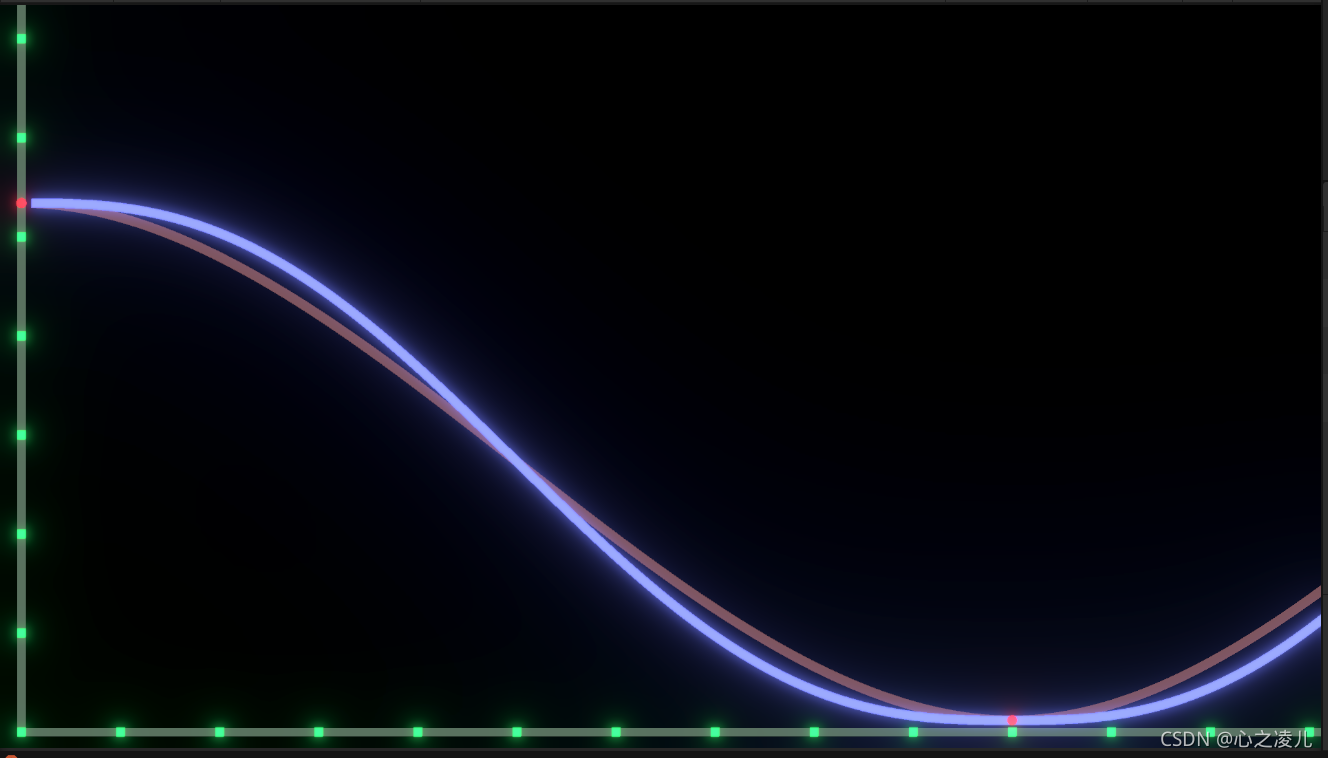
在这里插入图片描述

由于取值太小，对比不是很明显，所以我们放大X轴，就可以明显的看出，通过 $6t^{5}-15t^{4}+10t^{3}$ 插值求得的曲线在整数点附近的点位的斜率明显小于 $3t^{2}-2t^{3}$ 插值函数，如下图所示：

在这里插入图片描述

二维柏林噪声的演绎

基于一维柏林噪声，来思考二维Perlin Noise的生成，同样我们需要选取坐标的整数点来给以随机值，然后根据这些整数点的取值采取相应的插值策略来获取那些非整数值的数值，整个过程分为三部分：

类似于一维Perlin Noise，二维Perlin Noise会通过分别对于X轴与Y轴取整数点

在场景中创建一个三维坐标系，以X轴与Z轴组成的平面作为二维柏林噪声坐标点，而Y轴则代表每一个坐标的取值：

 public int posNumber;

    public GameObject posPre;

    public LineRenderer line1;
    public LineRenderer line2;
    public LineRenderer line3;
    private void Awake()
    {
        Coordinate();
    }

    void Coordinate()
    {

        line1.positionCount=posNumber;
        line2.positionCount=posNumber;
        line3.positionCount = posNumber;
        for (int i = 0; i < posNumber; i++)
        {
            GameObject goX = Instantiate(posPre, this.transform);
            goX.transform.position = new Vector3(i, 0, 0);
            line1.SetPosition(i, new Vector3(i, 0, 0));

            GameObject goY = Instantiate(posPre, this.transform);
            goY.transform.position = new Vector3(0, i, 0);
            line2.SetPosition(i, new Vector3(0, i, 0));

            GameObject goZ = Instantiate(posPre, this.transform);
            goZ.transform.position = new Vector3(0, 0, i);
            line3.SetPosition(i, new Vector3(0, 0, i));
        }
    }

执行代码，显示的效果如图：
在这里插入图片描述

实现一个坐标系的创建后，通过对于坐标系X轴与Y轴整数点来的选取Perlin Noise的基本点，为了避免与坐标系重叠，避开x=0与z=0的坐标点

在完成整数点的选取后，可以通过随机函数获取Y值，这样就可以在三维坐标系中确定唯一的位置：

 //获取整数点的数值，并实例化一个物体在该位置
    void CreatePoints()
    {
        for (int i = 0; i < v2.x; i++)
        {
            for (int j = 0; j < v2.y; j++)
            {
                float nub = UnityEngine.Random.Range(0, MaxNoise);
                GameObject go = Instantiate(itemPre, parent);
                go.transform.position = new Vector3(i+1, nub, j+1);
                items[i, j] = nub;

            }
        }
    }

执行上面的代码，就可以在场景中生成整数点对应的点位，这些点位可以作为基准点位来作为后面插值操作的基数点：

自由角度：
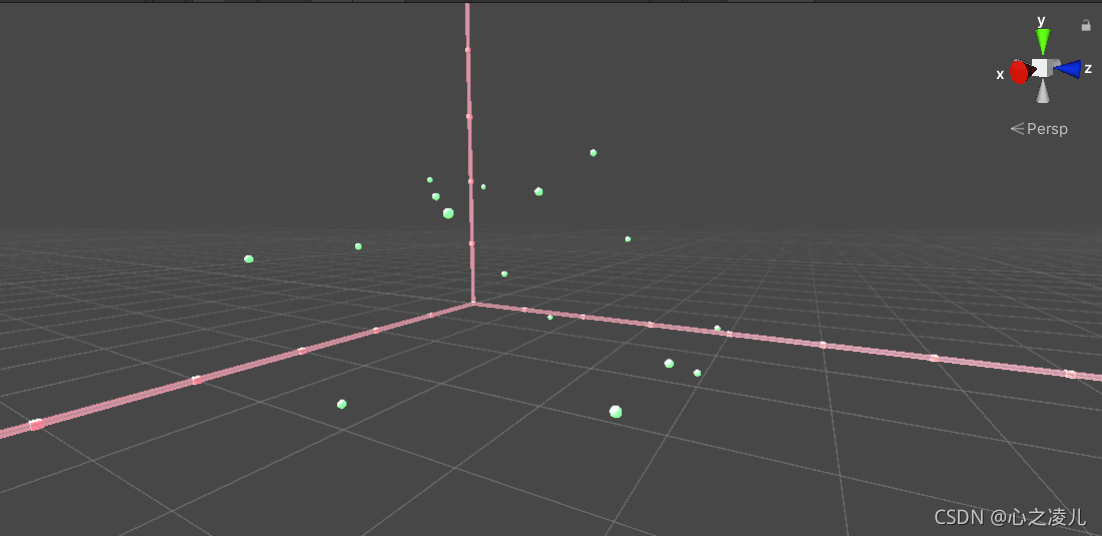
在这里插入图片描述

俯视角度：
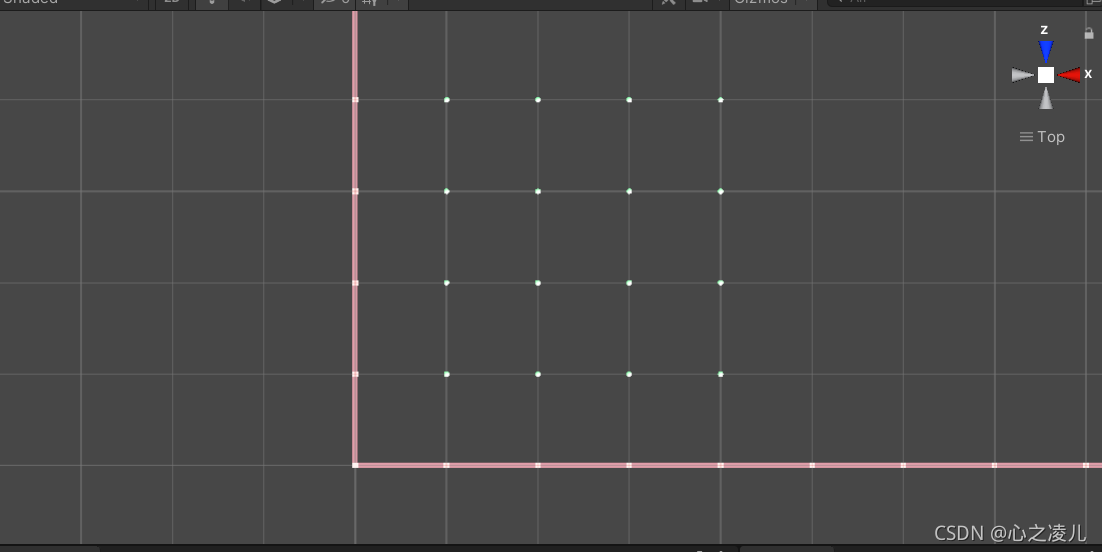
在这里插入图片描述

完成上面的准备工作，就来到了二维Perlin Noise的重点，如何通过插值获取非整数点的y值

不同于一维柏林噪声只需要执行一次插值操作即可求得对应的数字，二维柏林噪声需要根据距离其周围最近的四个整数点的数字来得到最后的结果，所以需要我们采取某种插值策略将四个数字联系起来

类似于双线性插值，Perlin Noise是通过三次插值来得到最终的结果的，在之前提到的维基百科中有介绍到：

在这里插入图片描述

简单的说就是，对于一个点在其最近四个坐标点组成的矩形内，如下图，对于E点，需要根据A 、B、C、D四个点的数值来插值获取，插值的逻辑是首先通过A点与D点的数值通过插值函数计算出F点的值，然后通过B点与C点的值计算出G点的数值，最后通过G与F两点的值插值获取到最终的数值。

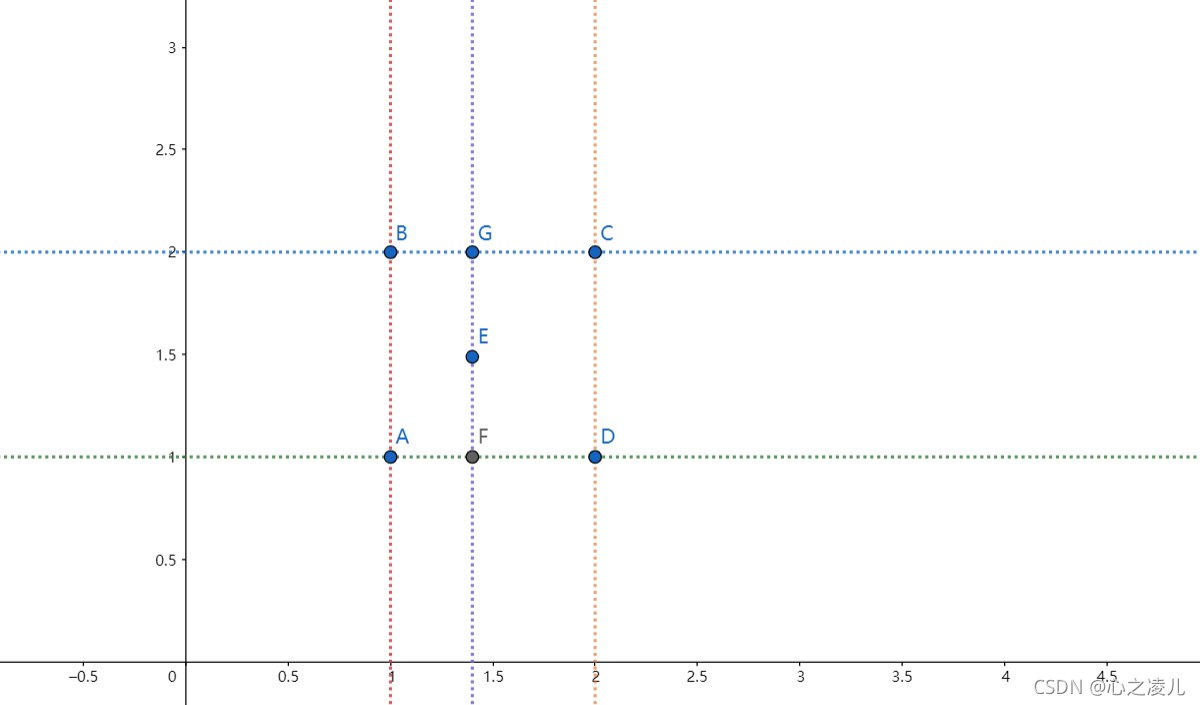
在这里插入图片描述

相比于一维Perlin Noise对于中间值的计算，，二维Perlin Noise只是多进行了两次插值操作，核心代码进行简单的改变：

    //计算四个相邻整数点组成的矩阵的点位的插值
 	public void CreateGrid(int x,int y)
    {
        for (int i = 0; i < 11; i++)
        {
            for (int j = 0; j < 11; j++)
            {
                float interX = Mathf.Lerp(items[x, y], items[x + 1, y], InterpolationCalculation1(i/10f));
                float interY = Mathf.Lerp(items[x, y+1], items[x + 1,y+1], InterpolationCalculation1(i / 10f));
                float inter = Mathf.Lerp(interX, interY, InterpolationCalculation1(j/ 10f));
                GameObject go = Instantiate(itemPre, parent);
                go.transform.position = new Vector3(x+ i /10f+1, inter, y+ j/10f+1);

            }
        }
    }

    //插值函数的计算
    float InterpolationCalculation1(float num)
    {
        return 6 * Mathf.Pow(num, 5) - 15 * Mathf.Pow(num, 4) + 10 * Mathf.Pow(num, 3);
    }

执行代码，可以看到二维柏林噪声的可视化效果：
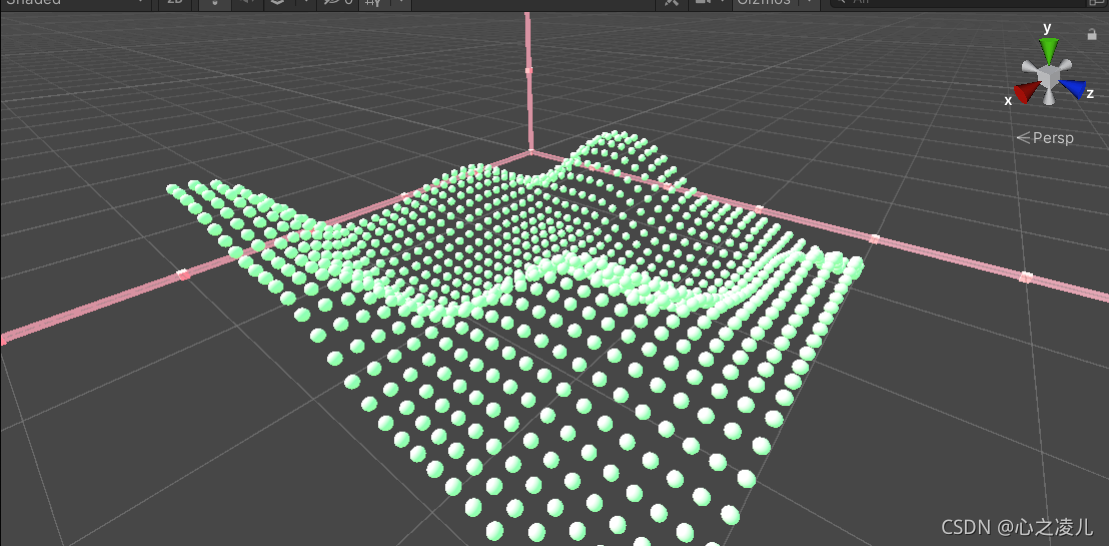
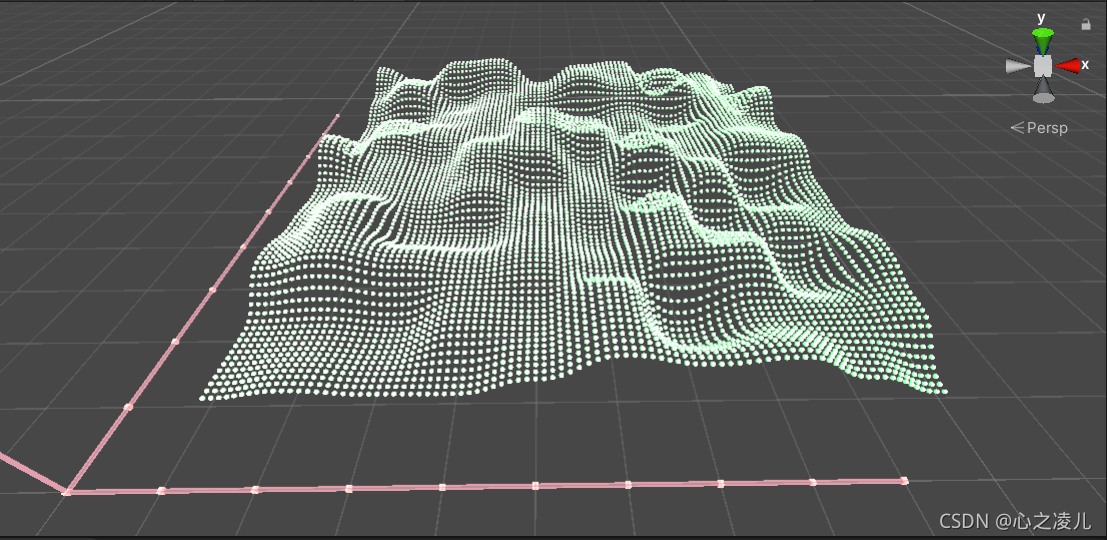
在这里插入图片描述

在这里插入图片描述

通过上面的图片可以看出基于二维Perlin Noise创建的图形与自然地形非常的接近，这也是为什么可以在地形创建上应用的原因

完善柏林噪声

前面也提到过，柏林噪声是一种伪随机的算法，每一次创建的地形应该在同一坐标点表现相同，但是在上面的演示中，每一个整数点的数值都是通过随机函数生成的，即每一次创建的地形都是完全随机的

在前面的演示中，完全随机影响到地形的因素只有整数点对应的数值，如果我们有一种方法，可以在某一状态下给定相同的数值，那么最终计算出来的地形也应该是相同的为了避免这样的问题，Perlin Noise提出了一种解决方法，给定整数点的初始值即可：

在这里插入图片描述

虽然已经给定了数组，但是并不是直接去使用其中的数值，而是经过一定规则的转换最终映射到一组范围比较小的梯度里面，关于梯度这部分比较复杂难懂，所以在上面并没有介绍到，只是简化思想的去演绎，整个具体的算法思想在后面有介绍，整个过程还是挺有意思的，有兴趣可以看看

小知识
在我的世界中，通过一串简单的种子数据就可以得到一个唯一的地形数据，最底层的那部分逻辑类似于柏林噪声的预设值处理

柏林噪声的算法思想

在上面的演示过程，为了避免晦涩难懂的数学知识，只是在应用层面上做出的处理。而若想要从理论知识上来理解，可以通过Ken Perlin给出的Java版本的源码来理解一下整个过程：

public final class ImprovedNoise
{
    static public double noise(double x, double y, double z)
    {
        int X = (int)Math.floor(x) & 255,                  // FIND UNIT CUBE THAT
            Y = (int)Math.floor(y) & 255,                  // CONTAINS POINT.
            Z = (int)Math.floor(z) & 255;
        x -= Math.floor(x);                                // FIND RELATIVE X,Y,Z
        y -= Math.floor(y);                                // OF POINT IN CUBE.
        z -= Math.floor(z);
        double u = fade(x),                                // COMPUTE FADE CURVES
               v = fade(y),                                // FOR EACH OF X,Y,Z.
                w = fade(z);
        int A = p[X] + Y, AA = p[A] + Z, AB = p[A + 1] + Z,      // HASH COORDINATES OF
            B = p[X + 1] + Y, BA = p[B] + Z, BB = p[B + 1] + Z;      // THE 8 CUBE CORNERS,

        return lerp(w, lerp(v, lerp(u, grad(p[AA], x, y, z),  // AND ADD
                                     grad(p[BA], x - 1, y, z)), // BLENDED
                             lerp(u, grad(p[AB], x, y - 1, z),  // RESULTS
                                     grad(p[BB], x - 1, y - 1, z))),// FROM  8
                     lerp(v, lerp(u, grad(p[AA + 1], x, y, z - 1),  // CORNERS
                                     grad(p[BA + 1], x - 1, y, z - 1)), // OF CUBE
                             lerp(u, grad(p[AB + 1], x, y - 1, z - 1),
                                     grad(p[BB + 1], x - 1, y - 1, z - 1))));
    }
    static double fade(double t) { return t * t * t * (t * (t * 6 - 15) + 10); }
    static double lerp(double t, double a, double b) { return a + t * (b - a); }
    static double grad(int hash, double x, double y, double z)
    {
        int h = hash & 15;                      // CONVERT LO 4 BITS OF HASH CODE
        double u = h < 8 ? x : y,                 // INTO 12 GRADIENT DIRECTIONS.
               v = h < 4 ? y : h == 12 || h == 14 ? x : z;
        return ((h & 1) == 0 ? u : -u) + ((h & 2) == 0 ? v : -v);
    }
    static final int p[] = new int[512], permutation[] = { 151,160,137,91,90,15,
   131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
   190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
   88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
   77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
   102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
   135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
   5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
   223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
   129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
   251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
   49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
   138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
   };
    static { for (int i=0; i< 256 ; i++) p[256 + i] = p[i] = permutation[i]; }
}

整个过程与上面的可视化演示差不多，但是在对于原理上的理解省略了一些知识，这里补充上，便于读者来学习理解，从代码出发，主要分为下面这几个步骤：

对于坐标的处理转换
基于给定数组获取整数点的哈希值
根据其周围的整数点的哈希值获取梯度
通过插值获取当前点位对应值

首先对于坐标点的处理，就是要根据当前传入的坐标的整数部分得到其周围整数点的坐标值，而小数位则作为一个基本单位里面插值定位的参数值：

		int X = (int)Math.floor(x) & 255,                  // FIND UNIT CUBE THAT
            Y = (int)Math.floor(y) & 255,                  // CONTAINS POINT.
            Z = (int)Math.floor(z) & 255;
        x -= Math.floor(x);                                // FIND RELATIVE X,Y,Z
        y -= Math.floor(y);                                // OF POINT IN CUBE.
        z -= Math.floor(z);

上面的代码，通过floor方法（向下取整）与位运算获取了两组数据:

（X，Y，Z)：向下取整除256取余，用于后续获取整数点的哈希值
（x，y，z）：减去向下取整的自身，简单来说就是对于最近的方块单位向0到1的映射

这里简单的介绍一下位运算，本质上就是转换成二进制来进行对位的操作，在Perlin Noise使用&的位运算本质上是为了求余，由于是位与位之间的操作，所以运行效率很高，具体的二进制计算为：

&代表与运算，其计算规则为：

1&1=1 1&0 =0  0&1 = 0 0&0 = 0

所以在本运算中，一个整数x与255 进行&运算,假设整数为257，则计算过程为：
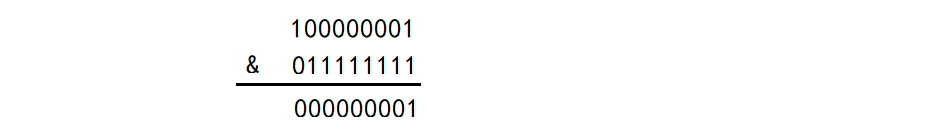
在这里插入图片描述

在上面的过程中，超出255的位经过与运算归零，而小于等于 255的与运算后等于其自身，达到求余的效果

之后就需要得到整数点计算出的哈希值，采用这一步的目的是为了对于二维或者更高维的坐标点做一个单项的排列，使得坐标点矩形单位可以对应单项数组：

        int A = p[X] + Y, AA = p[A] + Z, AB = p[A + 1] + Z,      // HASH COORDINATES OF
            B = p[X + 1] + Y, BA = p[B] + Z, BB = p[B + 1] + Z;      // THE 8 CUBE CORNERS,


    static final int p[] = new int[512], permutation[] = { 151,160,137,91,90,15,
   131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
   190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
   88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
   77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
   102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
   135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
   5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
   223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
   129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
   251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
   49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
   138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
   };
    static { for (int i=0; i< 256 ; i++) p[256 + i] = p[i] = permutation[i]; }

在代码中列出了三维案例中的四个点，同时在后面的计算中换算得到后面的四个点，通过代码可以看到一个整数点对应的数组值是通过坐标的三个轴进行的哈希换算

假设有一个坐标点A的坐标为（x,y,z),则通过哈希转换，从数组中拿到数据的代码结构为：

int posA=p[p[p[x]+y]+z];

同时由于数组中的数值为0到255不重复的数字，如果只这样进行下标的加法，明显会造成数组的越界。所以Ken Perlin选择将数组扩容至两倍来避免该问题

在从数组中拿到对应的数值后，就需要得到出整数点对应的梯度值与距离向量的点积，在这一过程中，需要了解整数点对应的梯度向量并不是计算而来，而是基于之前在数组中拿到的数字从给定的一些梯度中选择对应的梯度

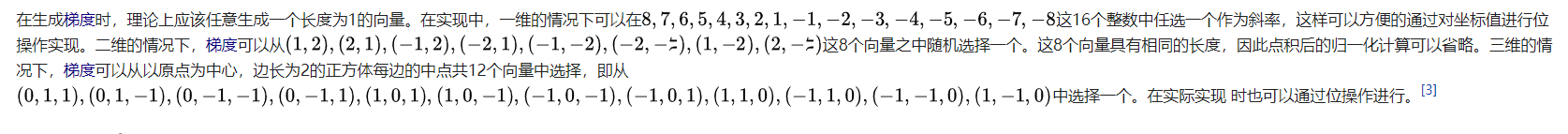
在这里插入图片描述

那么如何通过给定的数字来求得其对应的唯一梯度呢，Ken Perline在算法中使用了位翻转的操作来获取到最终的梯度，在代码案例中：

static double grad(int hash, double x, double y, double z)
    {
        int h = hash & 15;                      // CONVERT LO 4 BITS OF HASH CODE
        double u = h < 8 ? x : y,                 // INTO 12 GRADIENT DIRECTIONS.
               v = h < 4 ? y : h == 12 || h == 14 ? x : z;
        return ((h & 1) == 0 ? u : -u) + ((h & 2) == 0 ? v : -v);
    }

通过对于之前哈希转换获取的值与所求点位的小数坐标换算来得出所求整数点在当前梯度点的权重

在这一部分有一个数学概念：梯度

梯度表示某一函数在该点处的方向导数沿着该方向取得最大值，简单的来说，在三维空间内可以通过一个二维函数来表示一个曲面，如果指定y不变，可以得到一个伴随x变化而变化的曲线。这条曲线的函数就是二维函数的偏导数，而这条曲线上任何的一点的斜率，都可以通过一个向量表示，方向代表正负，长度代表大小。基于这样的想法，同样可以在该点相对于y的偏导数的斜率的向量，而这两个向量相加就是该点的梯度向量：