[游戏开发]在UE4引擎中做卡通描边的坑——角度加权平均修复顶点法线计算的错误误差

摘要

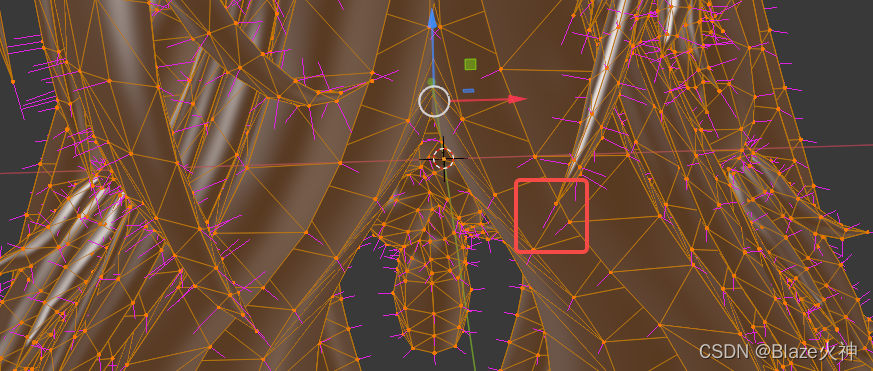
先直接上效果图，上图修复前，下图修复后：

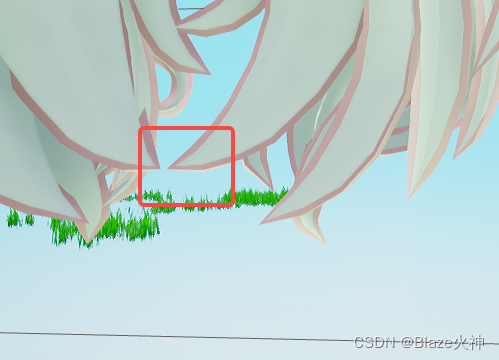
具体遇到的问题为：
模型包含平滑组，因此一个顶点存在多条法线。其中每一条法线可能从不同数量的三角面中加权平均得出，一旦各法线对应的三角面的数量不同，他们的权值也不同。因此直接用顶点法线求平均，无论怎么平均都不能保证结果正确，因为顶点法线已经丢失了权值信息。

所以，正确的方法应该是从面法线开始，重新计算法线，并加权平均，角度加权效果最好。

前情提要

工作中为了解决硬表面外描边断裂问题。参考了这个帖子，在模型导入ue4的时候，我计算了法线平均值并存到了切线。（还改进了一下算法时间复杂度）完成后用犹他茶壶检测了一下效果，还不错，就以为完结了。

然而几天后，TA报过来，边角的法线方向不对，是不是有些法线没算进去。
不应该啊，fbx是通过顶点序号判断是不是同一个点的，不需要计算距离，按说不会出现这种问题。

解决思路

调试了半天，打csv表排除了各种问题，最后用blender还原了一下流程。
首先看这个点的法线，因为有平滑组不同，有两根法线。

然后用blender合并法线，欧吼，blender算的法线方向也不正确

然后再用角度加权平均一下

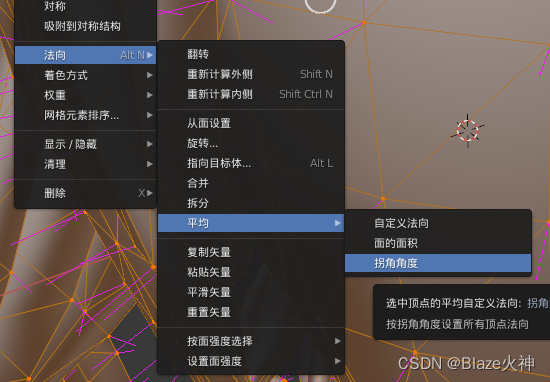
这样就对了！

结论：拿顶点法线直接计算是错误的。估计原因是平滑组计算出来的法线已经丢失了权重信息，直接平权平均加起来不能保证结果正确。（如果能分析出正确原因，欢迎指正）

实际代码

所以正确的做法是，计算面法线，再用面法线计算角度加权平均的顶点法线。
具体来说：如果一个控制点只有一条法线，那我就直接使用这条顶点法线；但如果有多条，那全不使用，从面法线开始从头计算。

void UnFbx::FFbxImporter::StoreAVGNormalsToTangent(FbxMesh* mesh)
{
	// 如果不存在 自动生成切线 副切线
	if (mesh->GetElementTangentCount() == 0 || mesh->GetElementBinormalCount() == 0)
	{
		mesh->GenerateTangentsData(0, true);
	}
	//获取layer
	FbxLayer* layer0 = mesh->GetLayer(0);
	//依次获取layer中的顶点色、2uv、法线、切线、副法线
	FbxLayerElementNormal* VertNormal = layer0->GetNormals();
	FbxLayerElementTangent* VertTangent = layer0->GetTangents();
	FbxLayerElementVertexColor* VertColor = layer0->GetVertexColors();
	TMap<int, FbxArray<FbxVector4>> VertexNormalsGroup;
	TMap<int, TArray<float>> VertexAngleWeightsGroup;
	TMap<int, FbxVector4> VertexAVGNormals;
	FbxVector4* AllControlPoints = mesh->GetControlPoints();

	//逐面片计算面法线
	//遍历面
	for (int i = 0; i < mesh->GetPolygonCount(); ++i)
	{
		//叉乘计算面法线
		FbxVector4 vtx0 = AllControlPoints[mesh->GetPolygonVertex(i, 0)];
		FbxVector4 vtx1 = AllControlPoints[mesh->GetPolygonVertex(i, 1)];
		FbxVector4 vtx2 = AllControlPoints[mesh->GetPolygonVertex(i, 2)];
		FbxVector4 edge1 = vtx1 - vtx0;
		edge1.Normalize();
		FbxVector4 edge2 = vtx2 - vtx1;
		edge2.Normalize();
		FbxVector4 TmpFaceNormal = edge1.CrossProduct(edge2);
		TmpFaceNormal.Normalize();
		
		//缓存面法线
		for (int j = 0; j < mesh->GetPolygonSize(i); ++j)
		{
			//获得控制点序号
			int vtxIdx = mesh->GetPolygonVertex(i, j);
			//获得控制点
			
			//计算角度权重
			int maxIdx = mesh->GetPolygonSize(i) - 1;
			//这个控制点
			FbxVector4 VtxAngel1 = AllControlPoints[mesh->GetPolygonVertex(i, j)];
			//上个控制点
			int index = (j - 1) >= 0 ? j - 1 : maxIdx;
			FbxVector4 VtxAngel0 = AllControlPoints[mesh->GetPolygonVertex(i, index)];
			//下个控制点
			int index2 = (j + 1) <= maxIdx ? j + 1 : 0;
			FbxVector4 VtxAngel2 = AllControlPoints[mesh->GetPolygonVertex(i, index2)];
			//计算角度
			FbxVector4 edgeAngle1 = VtxAngel0 - VtxAngel1;
			edgeAngle1.Normalize();
			FbxVector4 edgeAngle2 = VtxAngel2 - VtxAngel1;
			edgeAngle2.Normalize();
			double cosAngle = edgeAngle1.DotProduct(edgeAngle2);
			float angleWeight = (180.f) / PI * FMath::Acos(cosAngle);
			//将角度权重们、面法线们 以顶点序号为key 填入字典
			if (!VertexNormalsGroup.Contains(vtxIdx))
			{
				TArray<float> AngleWeights;
				AngleWeights.Add(angleWeight);
				VertexAngleWeightsGroup.Add(vtxIdx, AngleWeights);

				FbxArray<FbxVector4> Normals;
				Normals.Add(TmpFaceNormal);
				VertexNormalsGroup.Add(vtxIdx, Normals);
			}
			else
			{
				int nCount = VertexNormalsGroup[vtxIdx].Size();
				VertexNormalsGroup[vtxIdx].AddUnique(TmpFaceNormal);
				if(nCount != VertexNormalsGroup[vtxIdx].Size())
					VertexAngleWeightsGroup[vtxIdx].Add(angleWeight);
			}
		}
	}


	for (auto& kvp : VertexNormalsGroup)
	{
		FbxVector4 EqualWeightedSmoothNormal;
		if (kvp.Value.Size() == 1) 
		{
			VertexAVGNormals.Add(kvp.Key, kvp.Value[0]);
		}
		else
		{
			for (int n = 0; n < kvp.Value.Size(); ++n)
			{
				float angle=VertexAngleWeightsGroup[kvp.Key][n];
				FbxVector4 tmp = kvp.Value[n];
				tmp.Normalize();
				//万一法线模不为1，之前max脚本里看到过不是单位向量的法线
				EqualWeightedSmoothNormal = EqualWeightedSmoothNormal + tmp * angle;
			}
			EqualWeightedSmoothNormal.Normalize();
			VertexAVGNormals.Add(kvp.Key, EqualWeightedSmoothNormal);
		}
	}
	VertexNormalsGroup.Empty();

	//逐顶点遍历缓存法线信息
	for (int i = 0; i < mesh->GetPolygonVertexCount(); ++i)
	{
		int vtxIdx = mesh->GetPolygonVertices()[i];
		FbxVector4 Normal = VertNormal->GetDirectArray()[i];
		//将顶点法线们 以顶点序号为key 填入字典
		if (!VertexNormalsGroup.Contains(vtxIdx))
		{
			FbxArray<FbxVector4> Normals;
			Normals.Add(Normal);
			VertexNormalsGroup.Add(vtxIdx, Normals);
		}
		else
		{
			VertexNormalsGroup[vtxIdx].AddUnique(Normal);
		}
	}

	//只有一条法线使用原始数据（顶点法线）
	for (auto& kvp : VertexNormalsGroup)
	{
		if (kvp.Value.Size() == 1)
		{
			VertexAVGNormals[kvp.Key] = kvp.Value[0];
		}
	}
	VertexNormalsGroup.Empty();
	//改写顶点切线为法平均
	for (int j = 0; j < mesh->GetPolygonVertexCount(); ++j)
	{
		int vtxIdx = mesh->GetPolygonVertices()[j];
		VertTangent->GetDirectArray().SetAt(j, VertexAVGNormals[vtxIdx]);
	}
	VertexAVGNormals.Empty();
	
}

然后再导出导入回blender看一下。很好，法线正确了！