- 线性代数相关
- 向量点乘 → 获得方向
- 向量叉乘 → 获得左右&内外
- 线性变换:保持网格平行并等距分布的变换
线性变换具有的性质:
- 所有的线仍是直线(包括对角线)
- 原点还在原点,不发生移动
- 我们如何理解Transformation(变换)?
????????简单的,我们可以将其理解为一系列的步骤,通过这些步骤,得以实现从三维空间到二维影像的转变。

一、二维/三维变换?
-
缩放(Scale)

-
?对称(Reflection)

-
切变(Shear)

-
?旋转(Rotation)

-
?仿射变换 = 线性变换 + 平移变换

?齐次坐标:
????????由于2D变换没有偏置量,所以无法表示2D平移的操作,而齐次坐标主要作用是引入偏置量,将平移变换(Translate)统一归入2D变换,不希望平移变换区别于其他的2D变换。
????????同时齐次坐标可以区分点与向量,根据向量的平移不变性,向量的w轴为0,点的w轴为1。
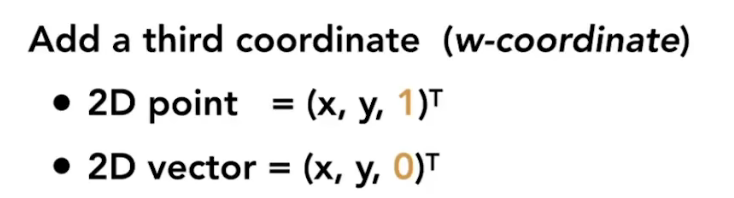
????????有了齐次坐标后,平移变换表示如下:?

-
?组合变换
? ? ? ? (1)基于旋转计算的特性(绕原点旋转),多个变换矩阵计算时一般先旋转后平移。


?????????(2)对于一个不在原点的图像,如何进行旋转变换?
????????先将图像平移到原点,变换操作结束后再平移会原位置。

-
基础变换矩阵总结

?二、MVP变换
????????MVP变换由三个变换组成,即Model Transformation、View / Camera Transformation、Projection Transformation。

-
Model transformation (placing objects)
????????将世界坐标系下的物体,用一个变化矩阵把它们的顶点坐标从局部Local坐标系(相对)转换到世界Global坐标系(绝对),即将DCC中的模型坐标转换为引擎中的模型坐标。
-
View transformation (placing camera)
????????将世界坐标系(世界中心为原点)转换到摄像机坐标系(摄像机所在位置为原点),实现第三视角向第一视角的转换。
????????(1)我们如何定义一个摄像机?
????????我们将摄像机的位置定义为,朝向定义为
,向上方向(类似于天线)定义为
。

????????(2) 如何实现M→V的转换?
????????将摄像机平移到原点,、
、
旋转到
、
、
。
????????其中,/
是摄像机向上方向(天线),
/
是摄像机观察方向,叉乘得到
/
。
????????由此、
、
模型空间坐标系转换成
、
、
观察空间坐标系。

? ? ? ?(3)如何计算目标旋转矩阵??????????
????????旋转矩阵求法:先求原点到相机的旋转矩阵,然后求逆得到相机到原点的旋转矩阵。
????????

????????注:旋转矩阵的逆矩阵 = 旋转矩阵的转置矩阵
-
Projection transformation
????????摄像机观察到的空间通常为一个视锥体,投影变换会将该视椎体变换成一个1×1×1的标准立方体,以方便后续操作的进行。
????????投影变换有两种形式,即透视投影(Perspective Projection)与正交投影(Orthographic Projection)。
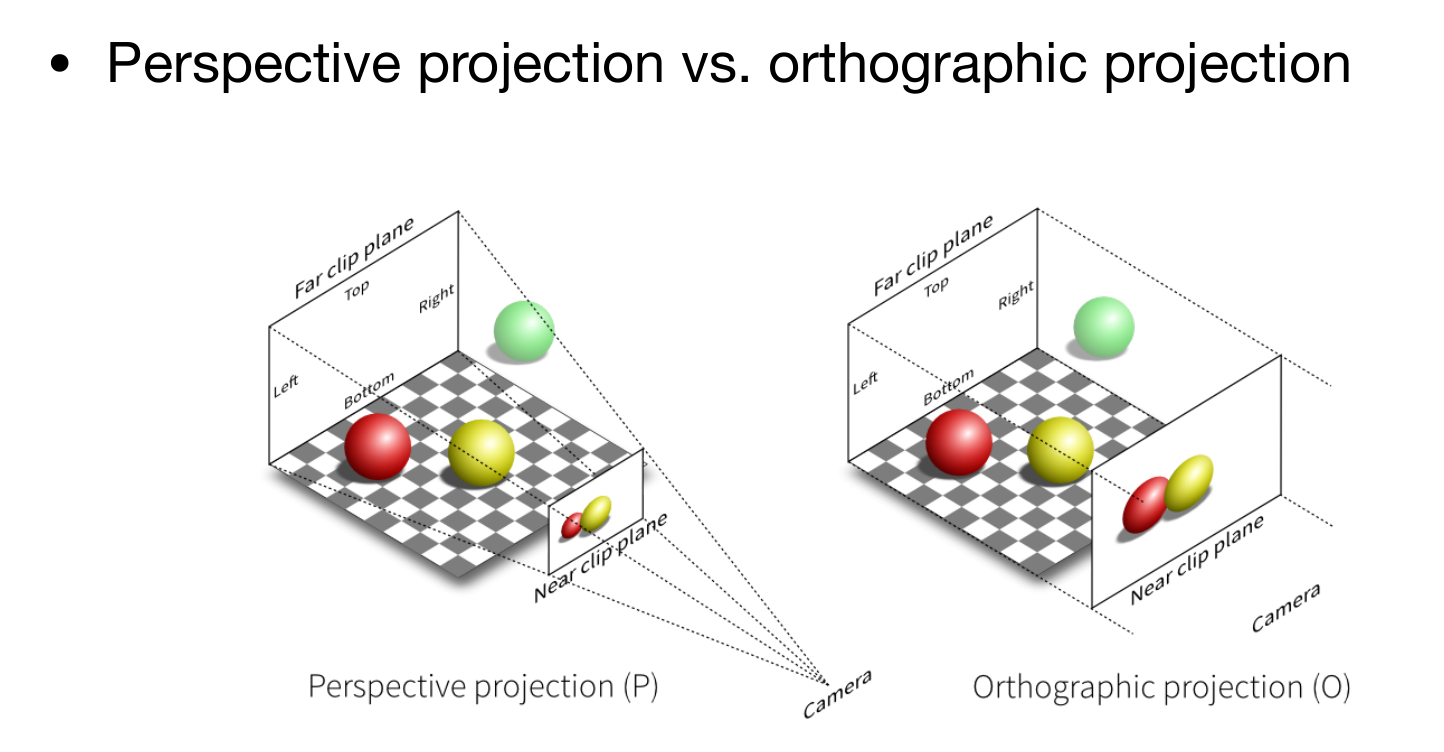
????????(1)正交投影(Orthographic Projection)
????????如何理解正交投影?

?? ? ? ? 我们将所有物体构成的空间设定为一个立方体,将该立方体通过平移与缩放,变为一个以原点为中心的1×1×1的标准立方体。

?????????变换矩阵如下:

????????(2)透视投影(Perspective Projection)
????????我们认为透视投影呈现出近大远小的现象,即与大部分相机、人眼的成像原理相同。
????????如何实现透视投影?
- 先把透视投影转换为到正交投影,即实现远平面到近平面的挤压
- 再做一次正交投影

?????????如何实现远平面到近平面的挤压?
????????首先得到屏幕宽高比,然后通过相似三角形进行计算。


?????????最终得到矩阵如下:
参考: