Lecture20
1 光场(Light Field)
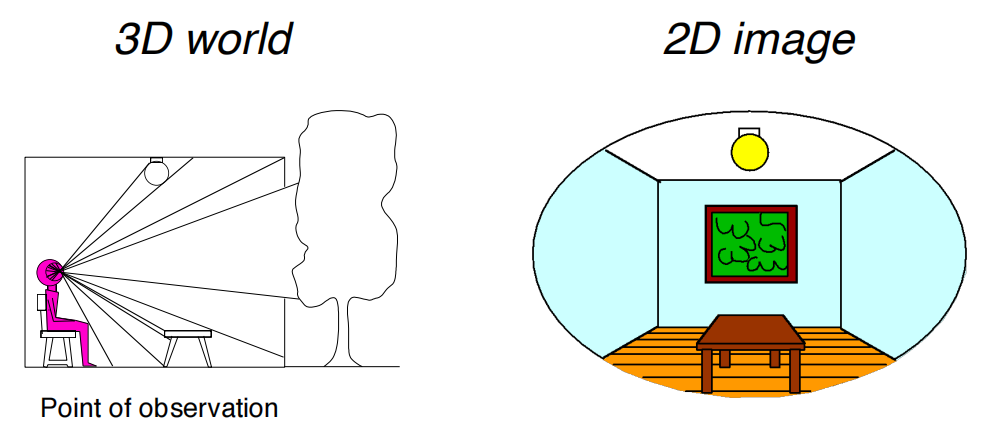
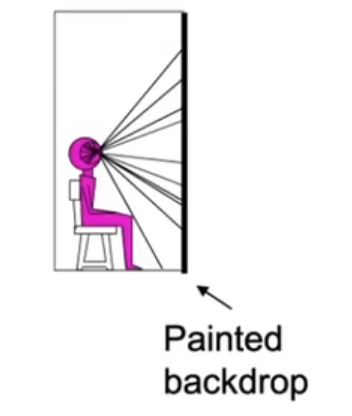
个案例:人坐在屋子里,用一张画布将人眼看到的东西全部画下来。
然后在人的前面摆上这个画布,以此2D图像替代3D场景以假乱真,这就是VR的原理。
1.1 全光函数(The Plenoptic Function)
光场描述空间中任意一点向任意方向的光线的强度。
而完整描述光场的全光函数是个7维函数,包含任意一点的位置(x, y, z)、方向(极坐标θ, φ)、波长(λ)(描述颜色)、时间(t)
全光函数描述了摄像机在任何位置,往任何方向看,在任何时间上看到的不同的颜色。


定义光线Ray
- 一般空间中的光线5D的:3D位置(x, y, z)+2D方向(θ, φ)。

- 光场中的光线为4D :2D位置+2D方向(θ, φ)。
如何理解?—— 位置并不是取物体表面的位置,而是取其包围盒平面的2维坐标。
用一个盒子包裹住物体,并且记录这个物体表面任何一个位置往各个方向发射的光的radiance。
相当于我们可以知道从外界任何一个位置任何一个方向看向该物体,有光场,我就应该知道能看到什么。
注意包围盒表面的2D坐标跟物体表面3D坐标是一一对应的。
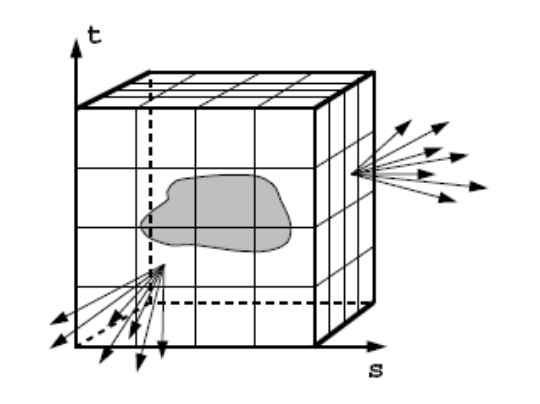
至此,我们其实并不关心物体是什么,当做黑盒,我只需要知道,从现在位置看过去,能看到什么。
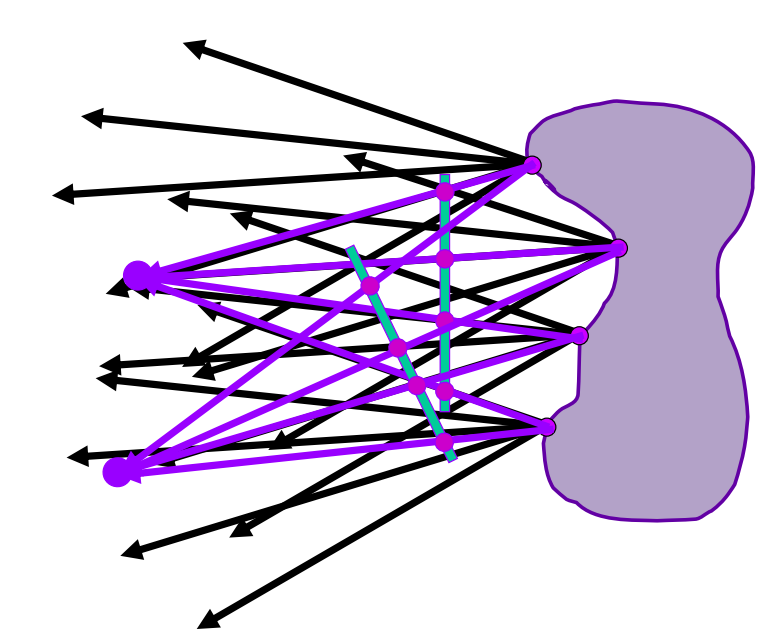
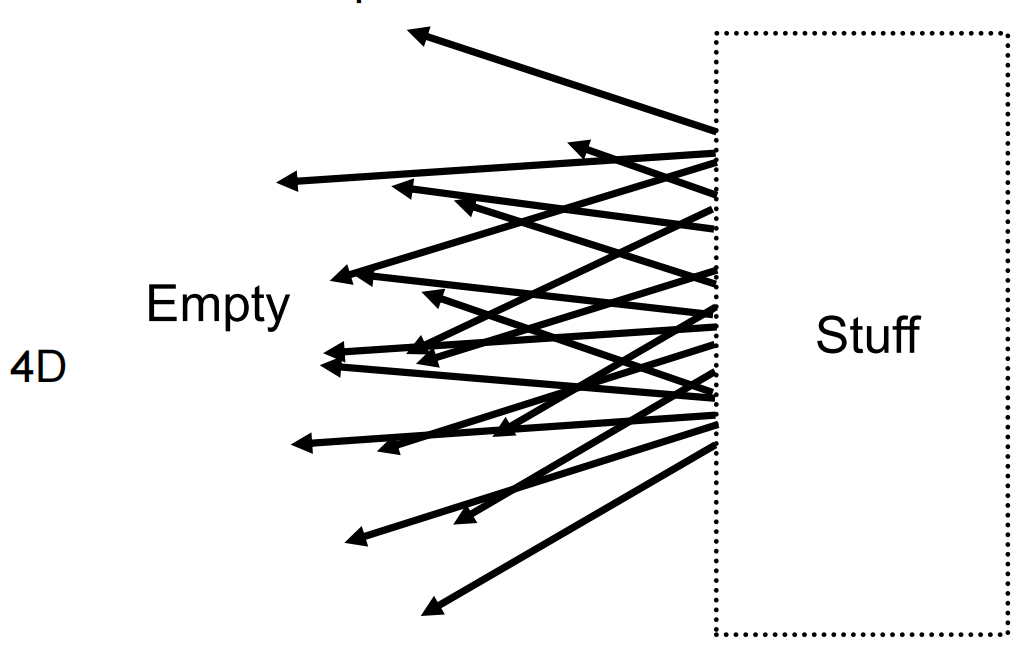
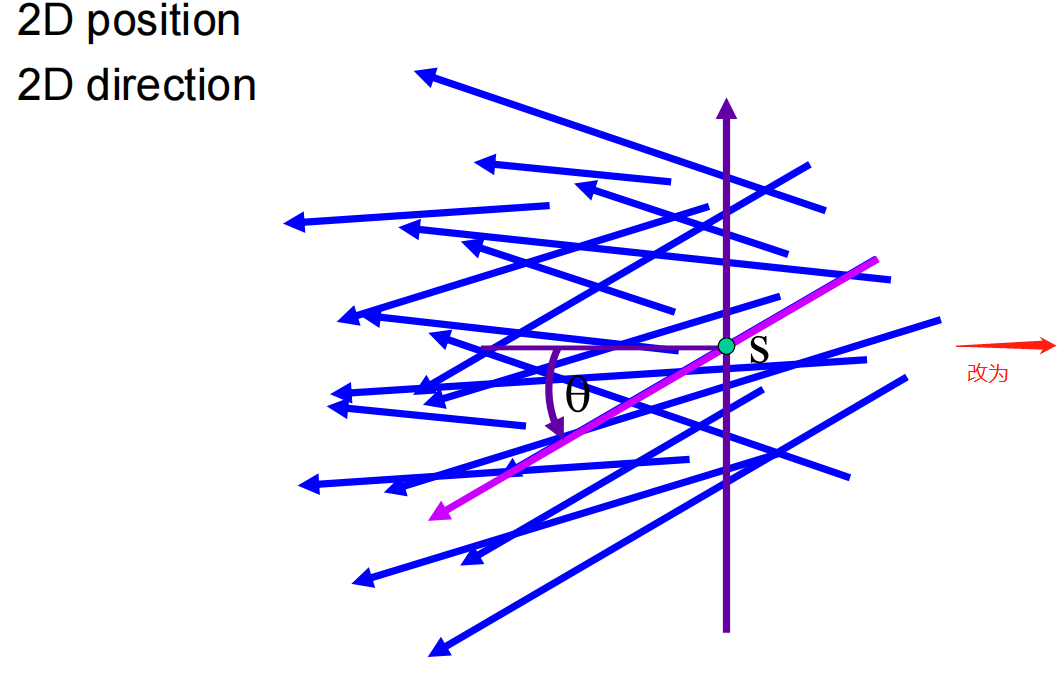
再升级一步,把光线的表示改为:2D位置+2D方向——>2D位置 + 2D位置
也就是用两个平面(分别是uv面和st面)上的两个点来表示一根光线(连接任意两个点就是一条线)
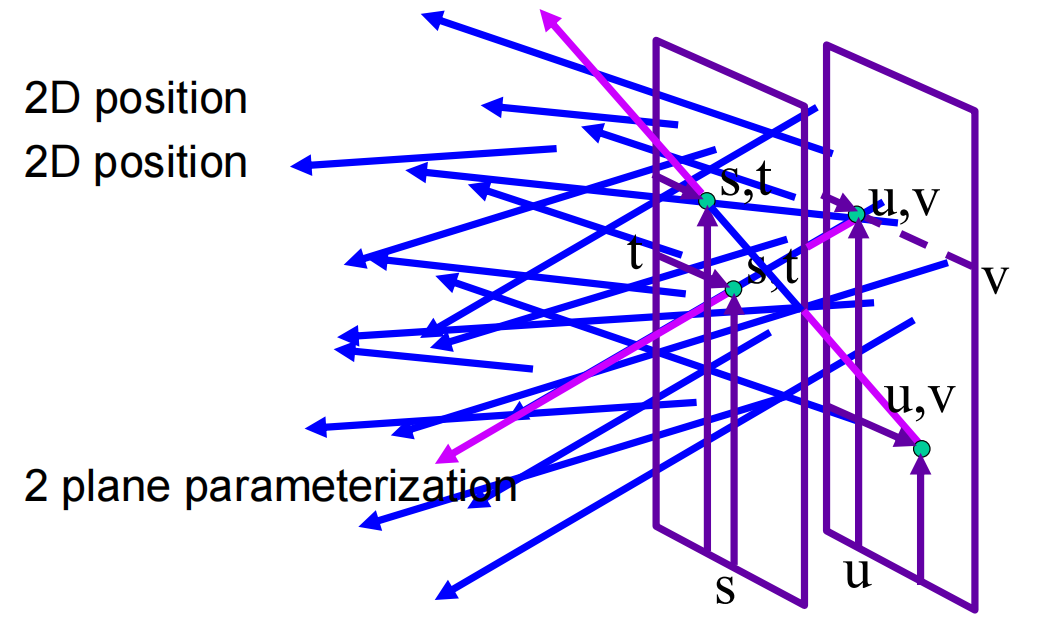
记录光场
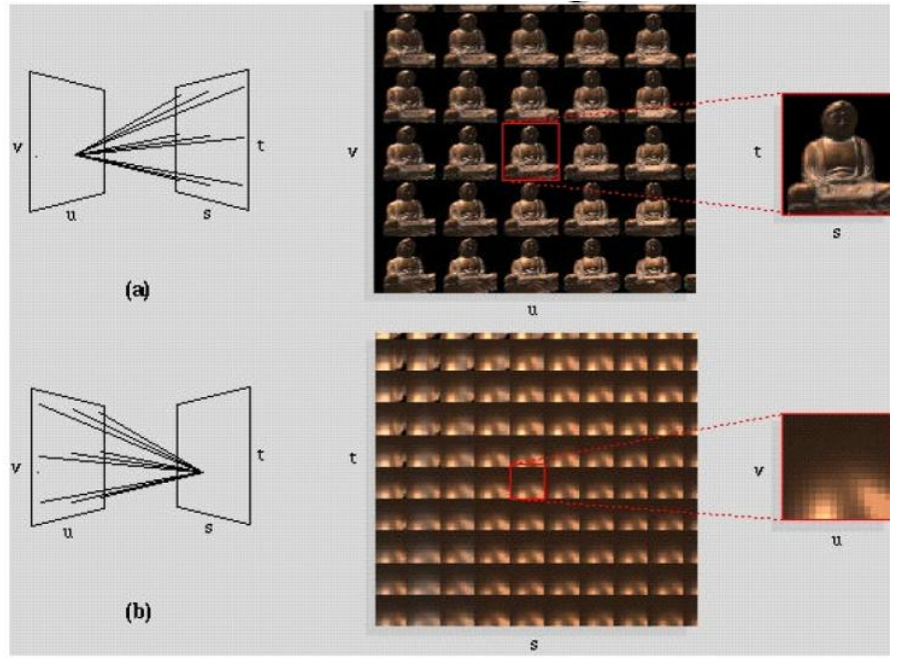
- 图(a):uv面上取一个点,看向st面,相当于一个针孔摄像机,能得到一张完整的图像。在所有uv的点对st平面(场景)进行拍摄,就会得到一堆拍摄角度不同的图像
- 图(b):如果固定st面上一点,看向uv平面,相当于我从所有不同的角度看向世界中的同一个点(比如佛像的眼珠)该是什么样,最终得到一堆角度不同的眼珠图。(另一种理解方式:每个像素存的是irradiance,遍历uv面所有点就是把irradiance展开成radiance)
1.2 光场照相机
Lytro相机,原理就是光场,由Prof.Ren Ng(UC Berkeley)发明。
其中最重要的功能:先拍照,后期动态调节聚焦
- 一般的摄像机传感器的位置在一排透镜所在的平面上,每个透镜就是一个像素,记录场景的irradiance。现在,光场摄像机将传感器后移一段距离,原本一个像素变成一个透镜,然后光穿过透镜后落在新的传感器上,击中一堆像素,这一堆像素记录不同方向的radiance。
- 光场摄像机拍出来的原始图片如下图所示,由一个个圆组成,如果把每个圆内所有像素求平均,可以得到原始照相机的成像结果。
- 怎么体现光场的原理?—— 从透镜所在平面往左看,不同的透镜对应不同的拍摄位置,每个透镜又记录了来自不同方向的radiance。总而言之,原本一个像素记录的irradiance,通过替换为透镜的方法,拆开成不同方向的radiance用多个像素存储。
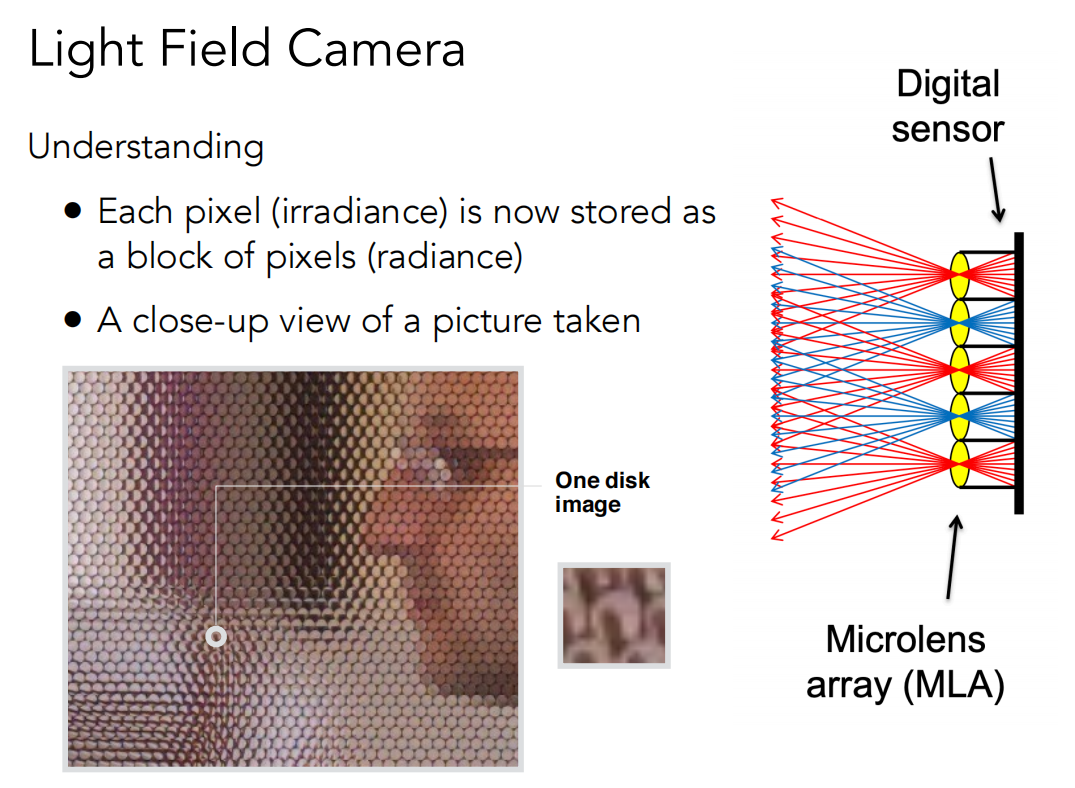
如何由光场摄像机图像得到普通的图像呢?
- 选择每个像素块的最下面一个像素,然后用这些像素拼成普通图像(实际上它们本来就是规则的矩阵)。
- 然后也能选择中间、上面等各个位置的像素
- 最终实现拍照后,再移动摄像机位置的效果。
对于如何实现后期变焦比较复杂,但思想很简单,首先我已经得到了光场,只需算出前后移动传感器,然后应该查询哪条光线,也可能对不同透镜查询不同位置的光线,这需要计算。
最后光场摄像机存在的不足之处
- 分辨率不足,原本1个像素记录的信息,需要可能100个像素来存储
- 高成本,为了达到普通相机的分辨率,需要更大的胶片,并且仪器造价高,设计复杂
2 颜色(Color)
2.1 颜色的物理学基础
光谱(Spectrum)
- 是复色光经过色散系统(如棱镜、光栅)分光后,被色散开的单色光按波长(或频率)大小而依次排列的图案,全称为光学频谱。
- 在图形学中,我们关注的是可见光光谱。
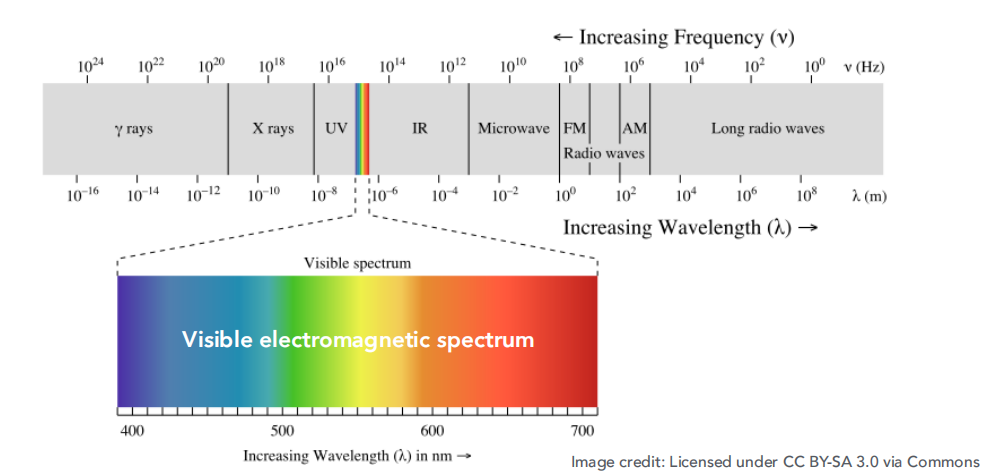
光谱功率分布(Spectral Power Distribution)(SPD)
- 描述光在各个波长上的分布情况
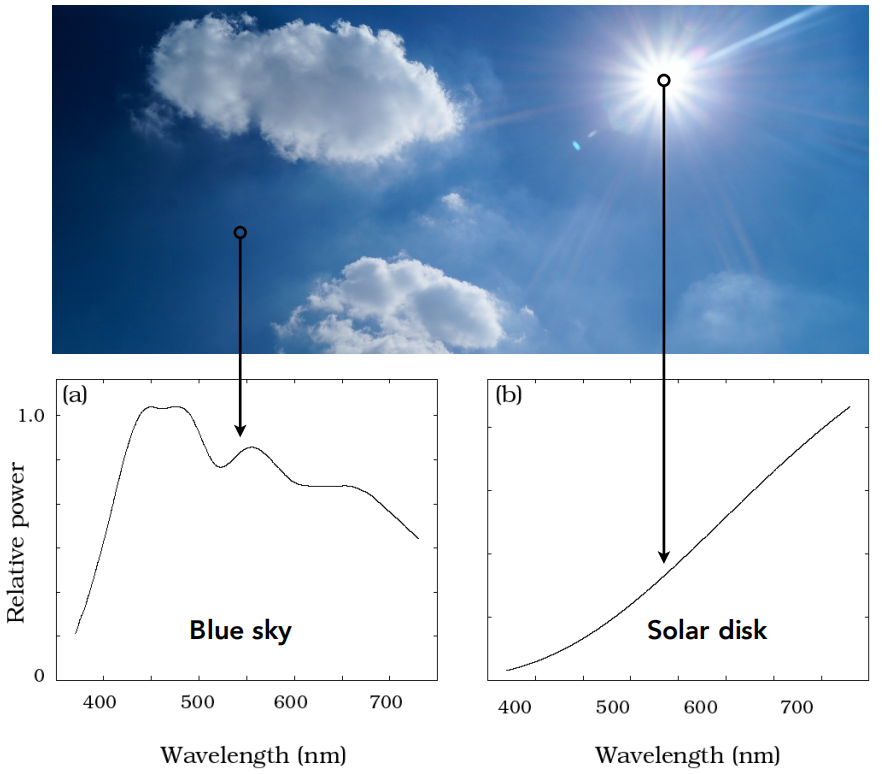
- 自然界中不同的光对应不同的SPD
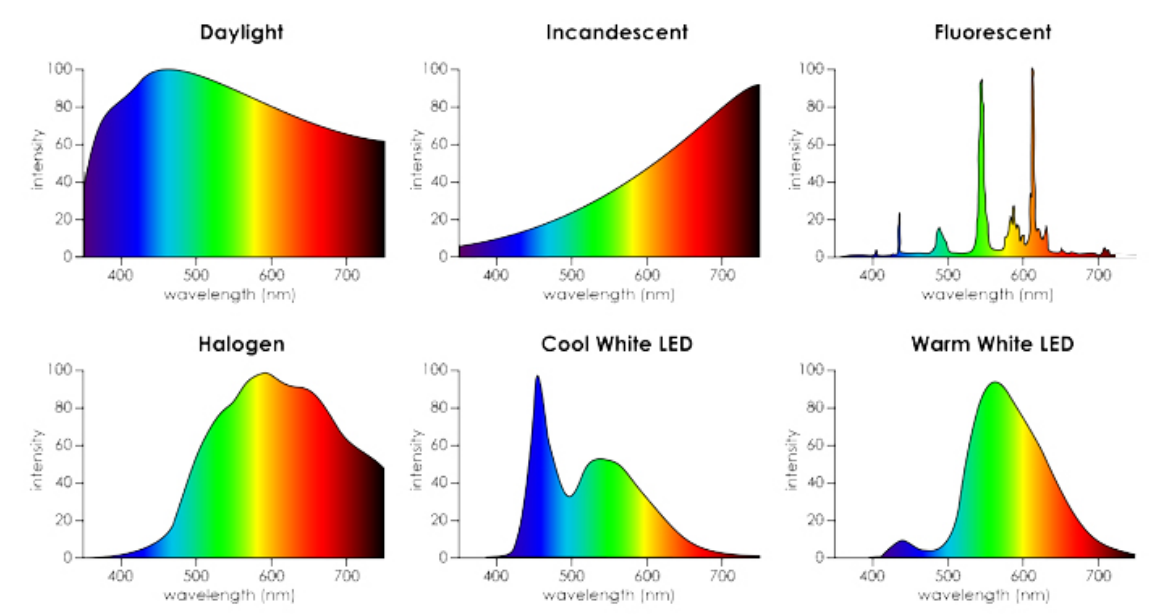
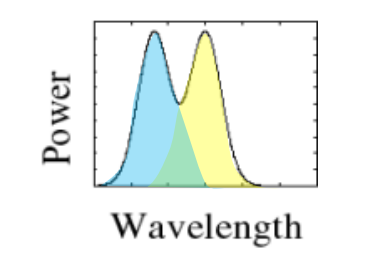
- SPD的线性性质
多种不同光叠加在一起,对应的SPD图也是简单的线性叠加
2.2 颜色的生物学基础
- 颜色是并不是光的普遍属性,而是人对光的感知。
- 不同波长的光 ≠ 颜色
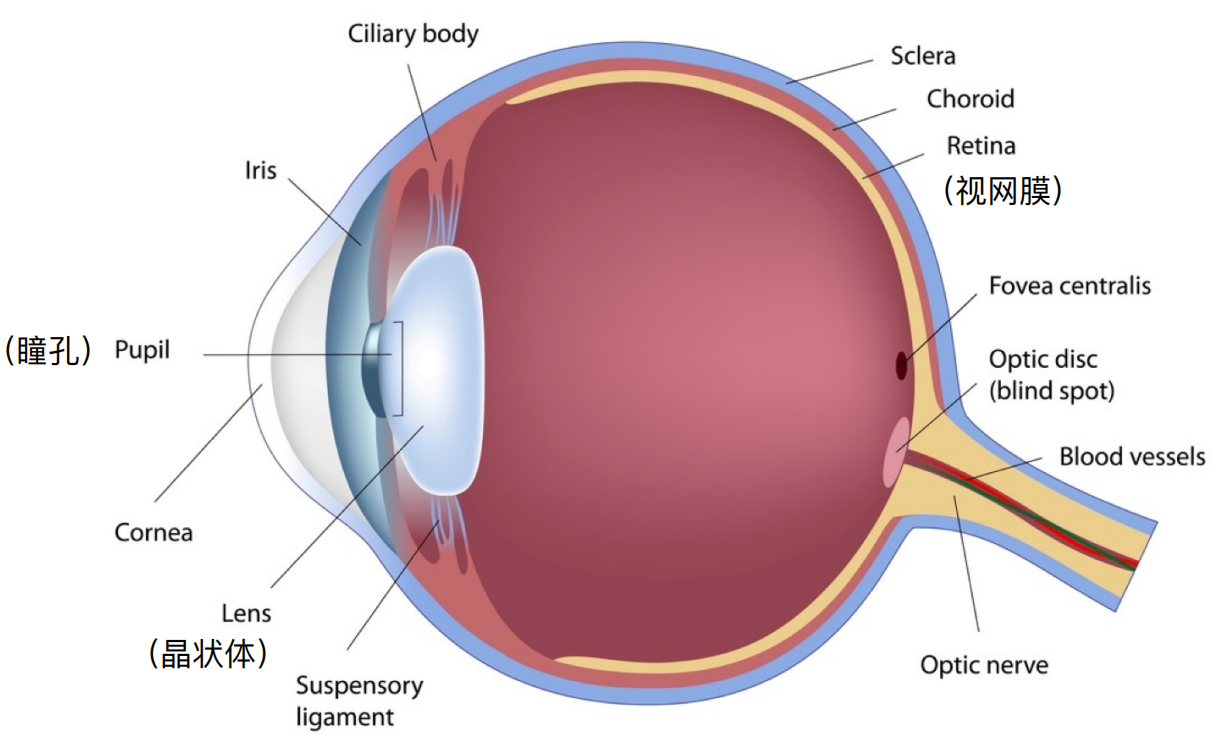
人眼球剖面图
- 人眼跟相机类似,瞳孔对应光圈,晶状体对应透镜,视网膜则是传感器(感光元件)
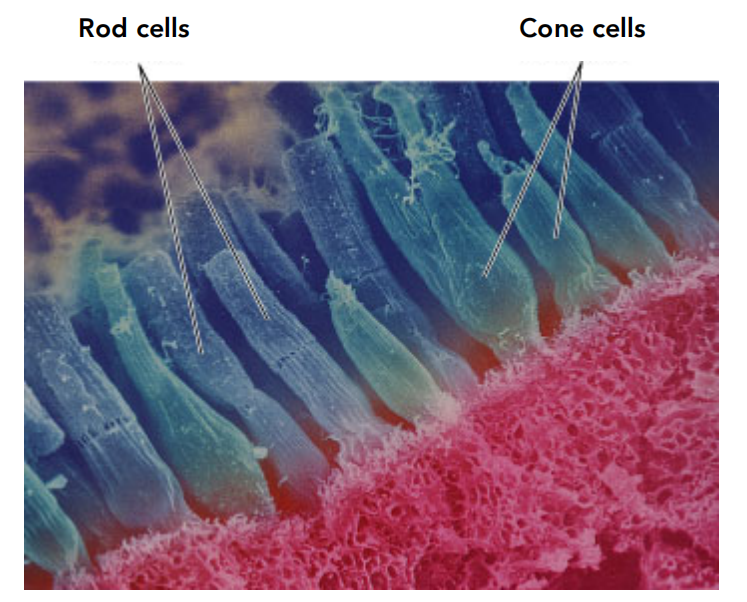
- 视网膜感光细胞:视杆细胞(Rods)、视锥细胞(Cones)
- Rods用来感知光的强度,可以得到灰度图
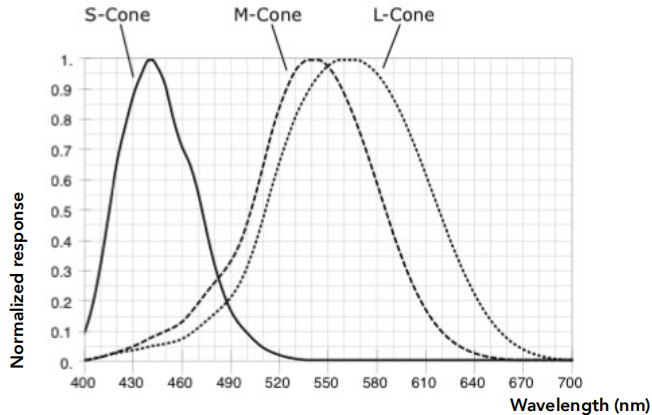
- Cones相对少很多,用来感知颜色,它又被分为3类(S-Cone、M-Cone、L-Cone)
- S M L三类细胞对光的波长敏感度(回应度) 不同,如右图所示
不同的人这三种细胞的比例和数量呈现很大的差异
下图是12个人这三种细胞的含量对比图

颜色的三刺激理论(Tristimulus Theory of Color)
三种不同细胞对于不同光是如何感知的?
- 将三种细胞的敏感度曲线(响应曲线)跟光的SPD相乘后做积分
- 最终返回人类感知到的三种颜色,SML对应三个数值
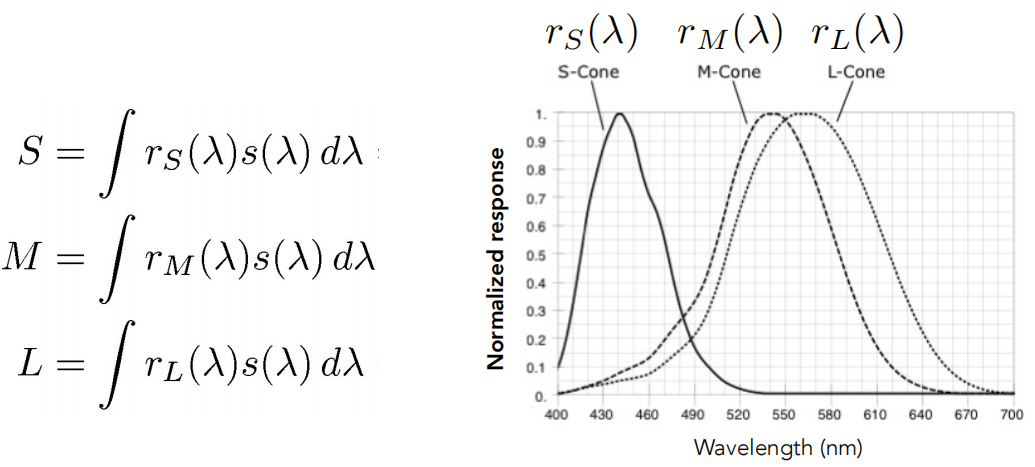
人看到的不是光谱,而是两种曲线积分后得到SML再叠加的结果。
那么一定存在一种现象:两种光,对应的光谱不同,但是积分出来的结果是一样的
同色异谱(Metamerism)
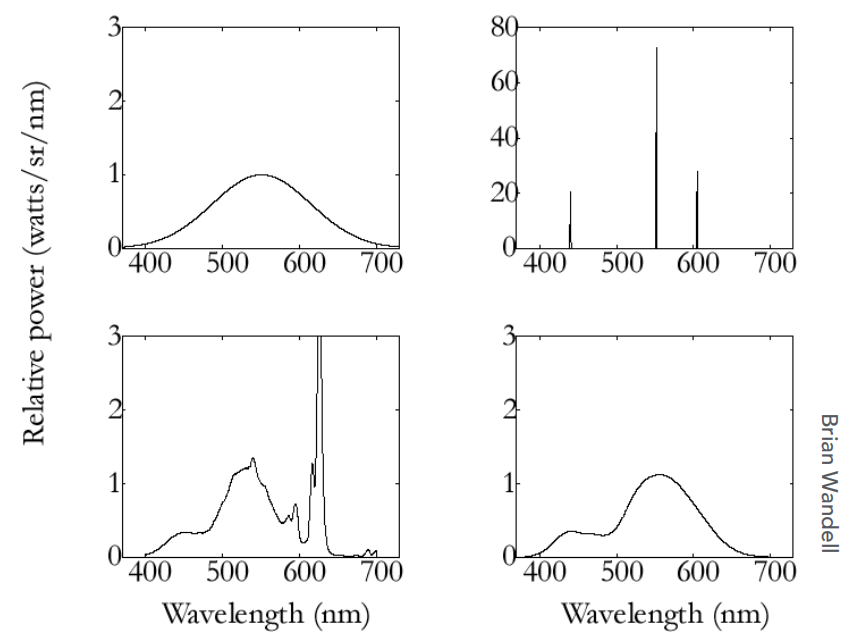
- 如下4种不同的SPD,经过响应曲线积分后,得到完全相同的结果。
- 比如现实中的太阳光谱如下,在显示器上可以用另一种光谱合成出一样的效果显示出来

2.3 色彩复制 / 匹配
- 计算机中的成色系统成为Additive Color(加色系统)
- 所谓加色法,是指颜色光的RGB三原色。它们按不同比例相加而混合出其他色彩的一种方法
CIE RGB颜色匹配实验
- 利用RGB三原色匹配单波长光(SPD表现为集中在一个波长上)
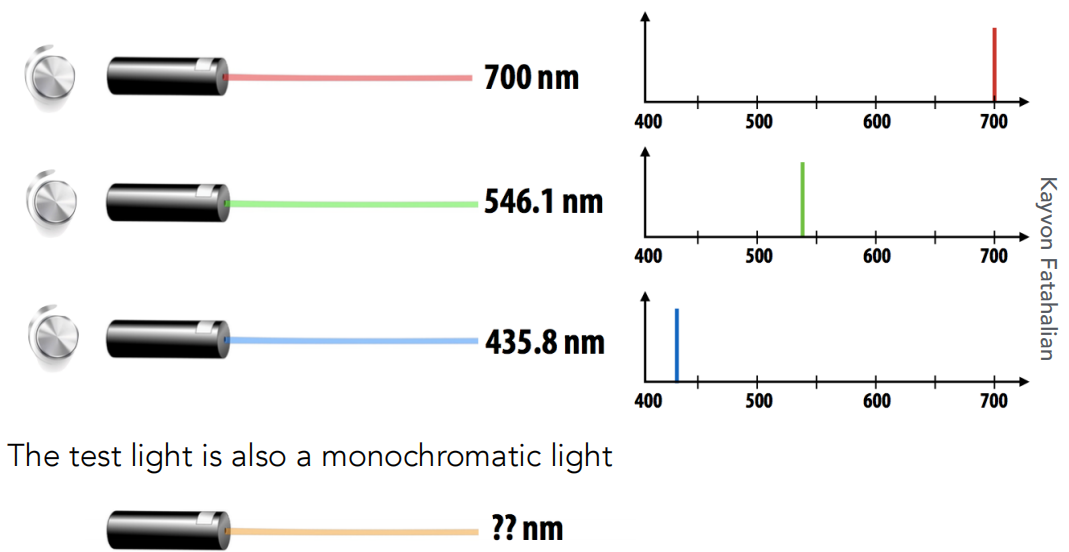
匹配曲线: 描述了每个CIE RGB原色光必须各自组合多少,以匹配在x轴上给出的波长的单波长光(目标测试光)
比如波长为600的光,大概需要的比例为1.15R、0.2G、0B。
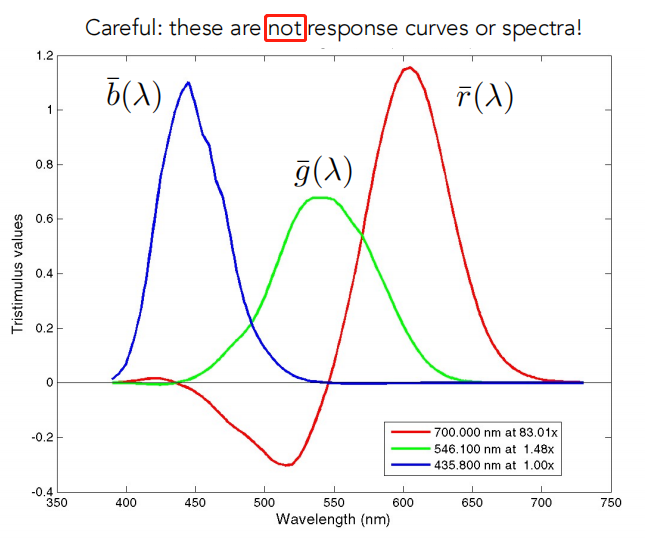
- 色匹配函数(非单波长光)
还是用RGB三原色,还是上面的匹配曲线,目标光变成了频谱分布不单一的光(比如下方这种SPD)
那就不能只考虑一个波长需要多少RGB,而是考虑全部波长范围,利用公式计算分别需要多少RGB(公式比较简单,就是带入RGB各自的匹配曲线的函数式,和目标光的频谱曲线函数,相乘并对横轴波长积分即可)
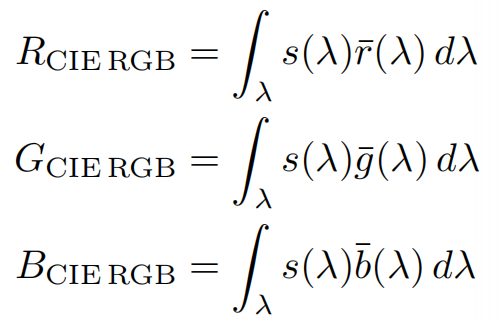

2.4 颜色空间(Color Spaces)
(1)Standardized RGB (sRGB)
多用于各种成像设备,上面介绍过,这里略。色域有限(大概为CIE XYZ的一半)。
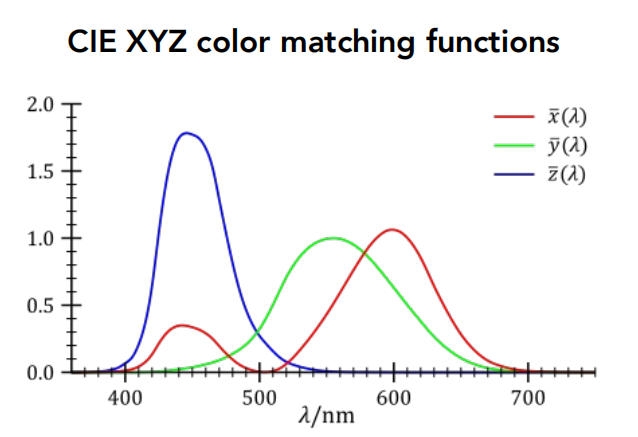
(2)CIE XYZ
广泛用于科学领域
- 这种颜色空间的匹配函数,对比之前的sRBG,没有负数段
- 匹配函数不是实验测出,而是人为定义的
- 绿色y的分布较为对称,用这三条匹配函数组合出来的 Y(类比之前的G) 可以一定程度上表示亮度
色域Gamut(所有可以显示的颜色)
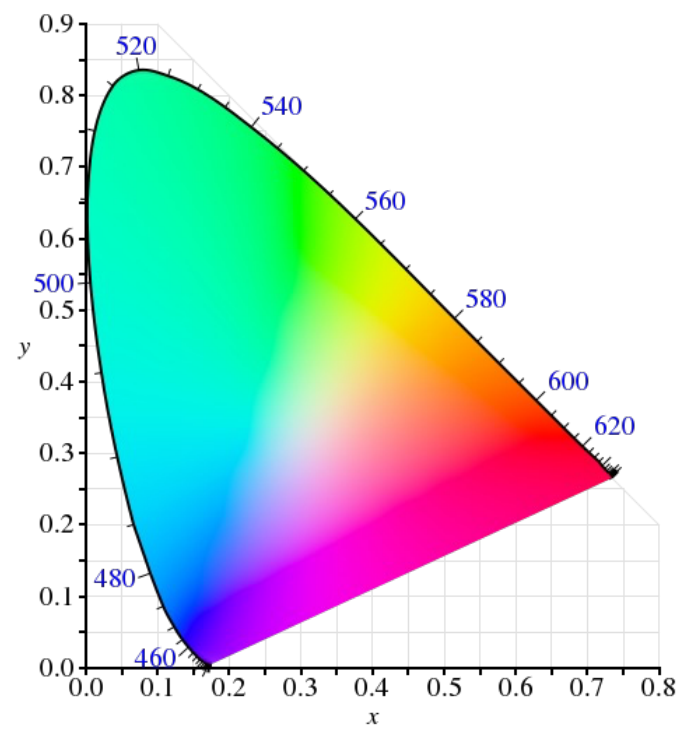
只是简单介绍,想更深入的学习,建议百度
(3)HSV
在颜色拾取器中广泛使用
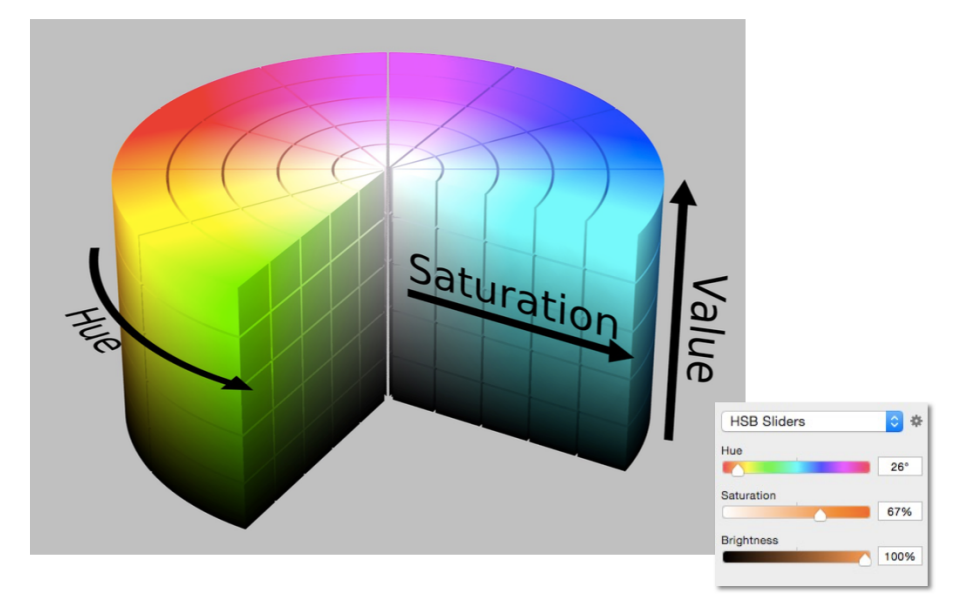
其他颜色空间略