?
VR技术:在VTK中构建一个与真实世界一样的虚拟相机,具有对应的运动映射。
?
?
一、解析
当我们使用SLAM技术获得相机的位姿Tcw时(即从世界坐标到相机坐标的映射矩阵),我们需要在VTK中建立一个一模一样的相机,并建立相同的运动映射。相机的位姿总共有六个自由度,在VTK中也应该有六个自由度。我们可以利用vtk的三个函数来进行设定:
aCamera->setFocalPoint(); //f=2
aCamera->setPosition(); //f=3
aCamera->setViewUp(); //f=1
前两个函数决定了5个自由度,最后一个决定了1个自由度
常用相机的坐标系如图所示:
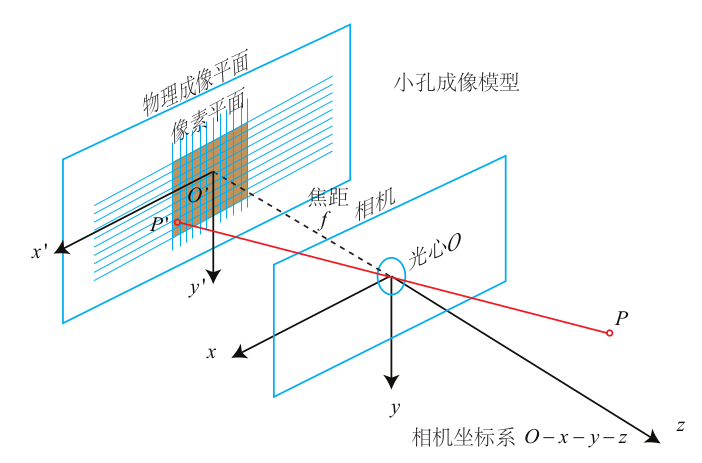
在VTK中相机位姿的表达:
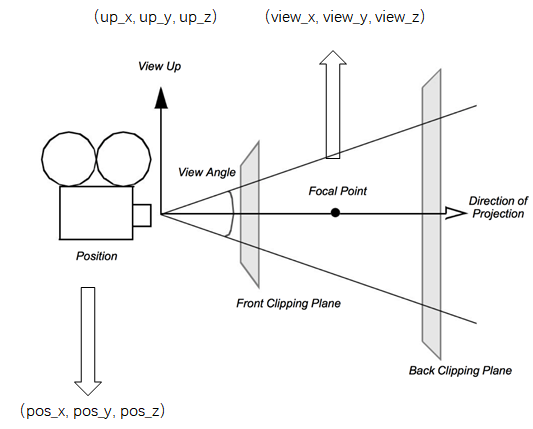
从图中我们可以确定的是,相机的位置(Position)表达是一样的,focalPoint是在相机的Z方向的,viewup是在常用坐标系y轴的负方向,这样我们就可以确定映射关系。
对于外参矩阵Tcw,可以拆成旋转矩阵Rcw 和平移矩阵 tcw,相机的位置可以表示为:
P
w
=
?
R
c
w
T
?
t
c
w
P_w = -R_{cw}^T\cdot t_{cw}
Pw?=?RcwT??tcw?
对于focalPoint,由相机的位置postion和focalPoint可以确定相机的朝向,这里就是常用坐标系的Z坐标轴方向。旋转矩阵的行、列分别代表了不同的意义:
行
:
O
x
w
c
,
O
y
w
c
,
O
z
w
c
列
:
N
x
c
w
,
N
y
c
w
,
N
z
c
w
行:Ox_{wc},Oy_{wc},Oz_{wc}\\ 列:Nx_{cw},Ny_{cw},Nz_{cw}
行:Oxwc?,Oywc?,Ozwc?列:Nxcw?,Nycw?,Nzcw?
行代表相机坐标的x,y,z轴在世界坐标系下的方向,列代表世界坐标系x,y,z轴在相机坐标系下的方向。这里只取旋转矩阵的第三行:
R
c
w
.
r
o
w
(
2
)
R_{cw}.row(2)
Rcw?.row(2)就能得到position到focalPoint也就是相机坐标Z轴的方向向量,同时第二行的负值:
?
R
c
w
.
r
o
w
(
1
)
-R_{cw}.row(1)
?Rcw?.row(1)就能代表viewUp.
二、方法
R = Tcw.rotation()
t = Tcw.translation()
eye = - R.transpose() * t //位置
focus = eye + R.row(2).transpose() //focalPoint 的位置(相机Z轴)
up = - R.row(1) //up方向(相机y轴负方向)
aCamera->setPosition(eye);
aCamera->setFocalPoint(focus);
aCamera->setViewUp(up);
最后重置视平面法向量:
aCamera->ComputeViewPlaneNormal()
显示:
ren->SetActiveCamera(aCamera)
renwin->Render();