题目

给你一棵根节点为 0 的二叉树，它总共有 n 个节点，节点编号为 0 到 n - 1 。同时给你一个下标从 0 开始的整数数组 parents 表示这棵树，其中 parents[i] 是节点 i 的父节点。由于节点 0 是根，所以 parents[0] == -1 。

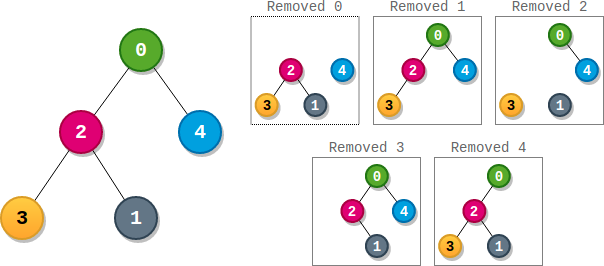
一个子树的大小为这个子树内节点的数目。每个节点都有一个与之关联的分数。求出某个节点分数的方法是，将这个节点和与它相连的边全部删除，剩余部分是若干个非空子树，这个节点的分数为所有这些子树大小的乘积。

请你返回有最高得分节点的数目。

示例 1:

输入：parents = [-1,2,0,2,0]
输出：3
解释：

节点 0 的分数为：3 * 1 = 3
节点 1 的分数为：4 = 4
节点 2 的分数为：1 * 1 * 2 = 2
节点 3 的分数为：4 = 4
节点 4 的分数为：4 = 4 最高得分为 4 ，有三个节点得分为 4 （分别是节点 1，3 和 4 ）。

示例 2：

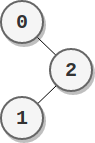
输入：parents = [-1,2,0]
输出：2
解释：

节点 0 的分数为：2 = 2
节点 1 的分数为：2 = 2
节点 2 的分数为：1 * 1 = 1 最高分数为 2 ，有两个节点分数为 2 （分别为节点 0 和 1 ）。

提示：

n == parents.length
2 <= n <= 105
parents[0] == -1
对于 i != 0 ，有 0 <= parents[i] <= n - 1
parents 表示一棵二叉树。

答案

链接

暴力解法

class nodeinform{
public:
    int totalchildnum;
    vector<int> childno;
    nodeinform() {
        //childnum = 0;
        totalchildnum = 0;
        childno.clear();
    }
};

map<int,nodeinform> buf;

void bfs(int parent) {
    for(int i=0;i<buf[parent].childno.size();i++) {
        bfs(buf[parent].childno[i]);
        buf[parent].totalchildnum += buf[buf[parent].childno[i]].totalchildnum;
    }
    buf[parent].totalchildnum +=buf[parent].childno.size();
    
}


class Solution {
public:


    int countHighestScoreNodes(vector<int>& parents) {
            
        // for(int i=0;i<parents.size();i++) {
        //     buf[i].totalchildnum = 0;
        // }

        for(int i=0;i<parents.size();i++) {
            //buf[parents[i]].childnum++;
            buf[parents[i]].childno.push_back(i);
            
        }


        bfs(0);

        //  for(int i=0;i<parents.size();i++) {  //打印会超时的
        //     cout <<  buf[i].totalchildnum << " ";
        //     for(auto s : buf[i].childno) {
        //         cout << s << " ";
        //     }
        //     cout << endl;
        // }

        stack<long> maxnumstack;

        
        long multiresult = 0;
        for(int i=0;i<parents.size();i++) {
            if(i==0) { // 0 - 2 个
                if(buf[i].childno.size()==0) {
                    multiresult = parents.size() - 1;
                }
                else if(buf[i].childno.size()==1) {
                    multiresult = parents.size() - 1;
                }
                else if(buf[i].childno.size()==2) {
                    multiresult = (long)(buf[buf[i].childno[0]].totalchildnum  + 1) * (buf[buf[i].childno[1]].totalchildnum + 1);
                }

            }
            else {  //0 - 3 个
                if(buf[i].childno.size()==0) {
                    multiresult = parents.size() - 1;
                }
                else if(buf[i].childno.size()==1) {
                    multiresult = (long)(buf[buf[i].childno[0]].totalchildnum + 1) * (parents.size() - 2 - buf[buf[i].childno[0]].totalchildnum);
                }
                else if(buf[i].childno.size()==2) {
                    multiresult = (long)(buf[buf[i].childno[0]].totalchildnum + 1) * (buf[buf[i].childno[1]].totalchildnum + 1) * (parents.size() - 3 - buf[buf[i].childno[0]].totalchildnum - buf[buf[i].childno[1]].totalchildnum);
                }
            }

            if(maxnumstack.empty() || multiresult >= maxnumstack.top()) {
                maxnumstack.push(multiresult);
            }
           
        }

        int maxmultiresultcount = 0;
        long maxmultiresult = 0;
        maxmultiresult = maxnumstack.top();

        while(!maxnumstack.empty() && maxmultiresult == maxnumstack.top()) {   
            maxmultiresultcount++;
            maxnumstack.pop();
        }

        buf.clear(); //需要清空否则提交多次测试时会保留全局变量的结果
        while(!maxnumstack.empty())
            maxnumstack.pop();
        return maxmultiresultcount;

    }
};