最近有了一些空闲时间,温故一下高中数学知识~
了解圆的标准方程:(x-a)2+(y-b)2=r2
(x-a)2+(y-b)2=r2 表示圆心坐标为(a,b),半径为r的圆。
个人思路:
知道了圆心坐标和圆的半径,我们也可以知道圆的最左端的坐标和最右端的坐标,这里只需要知道最左端的坐标的x值和最右端坐标的x值,两值之间分割得到多个点,将这些点代入方程求y值,会得到两个或一个y值,均作为二维向量数据存储下来,最后根据二维向量数据做点的连接就Ok。(知识水平表达能力有限)
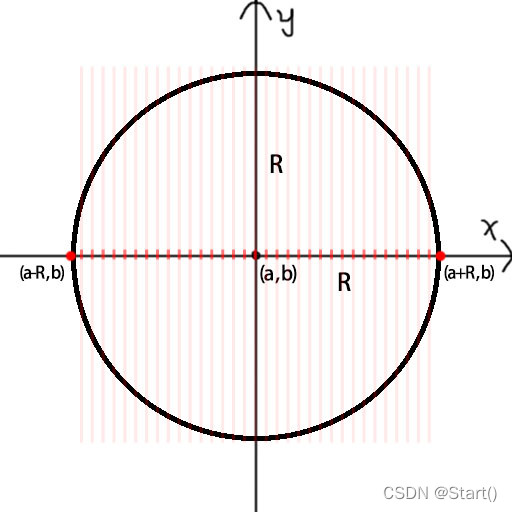
C# 实现 圆的标准方程 函数:
其中需要解一元二次方程式:
标准形式: ax2+bx+c=0(a≠0)
求根公式: x=[-b±√(b2-4ac)]/2a
using UnityEngine;
public class BiaoZhunFangCheng
{
/// <summary>
/// (x-a)2+(y-b)2=R2
/// 已知a、b、R,给出x,求y
/// </summary>
/// <param name="x">x</param>
/// <param name="center">中心点坐标(a,b)</param>
/// <param name="r"></param>
/// <returns>y一般有两值</returns>
private Vector2 GetYValue(float x, Vector2 center, float r = 1f)
{
//求出(x-a)2
float x_a2 = Mathf.Pow(x - center.x, 2);
//求出R2
float R2 = Mathf.Pow(r, 2);
//(x-a)2 减去 R2 得到一个值
float value = x_a2 - R2;
//(y-b)2与这个减值的和等于 0
//于是得到 (y-b)2 + value = 0
//在根据平方根公式:(y-b)2就等于 y2+b2-2yb
//于是得到 y2+b2-2yb + value = 0,其中的b和value是已知的,于是得到
//y2-2by + (value+b2) = 0,就得到了一个一元二次方程 ax2+bx+c=0
//其中 a = 1,b = 2b , c = (value+b2)
//代入写好的函数得到y值
Vector2 yValue = YiYuanErCi(a: 1, b: 2 * center.y, c: value + Mathf.Pow(center.y, 2));
return yValue;
}
/// <summary>
/// ax2+bx+c=0(a≠0)
/// 一元二次方程求根公式:x=[-b±√(b2-4ac)]/2a
/// </summary>
/// <param name="a">a</param>
/// <param name="b">b</param>
/// <param name="c">c</param>
/// <returns>结果一般会有两个值</returns>
private Vector2 YiYuanErCi(float a, float b, float c)
{
//x=[-b±√(b2-4ac)]/2a
float v1 = (-b + Mathf.Sqrt(Mathf.Pow(b, 2) - 4 * a * c)) / (2 * a);
float v2 = (-b - Mathf.Sqrt(Mathf.Pow(b, 2) - 4 * a * c)) / (2 * a);
return new Vector2(v1, v2);
}
}
线段分割
例如:从0 ~ 1,
我想分割为三个点,就是0,0.5,1
我想分割为四个点,就是0,0.3333…,0.6666…,1
我应该怎样实现呢?
/// <summary>
/// 获得从某点到某点分割的点
/// </summary>
/// <param name="formPoint">起始点</param>
/// <param name="toPoint">结束点</param>
/// <param name="whatPoint">分割为几点</param>
/// <returns>点值列表</returns>
public List<float> GetPoints(float formPoint, float toPoint, int whatPoint)
{
if (whatPoint <= 2)//最少两个点
return new List<float>() { formPoint, toPoint };
if (formPoint == toPoint)
{
Debug.LogError("起始点与结束点位置相同!");
return new List<float>() { formPoint };
}
//获取线段的长度
float chaZhi = toPoint - formPoint;
//段数比点数少一个
//像“10米距离能种11棵树”一个到了
int whatDuan = whatPoint - 1;
//通过段数获取每段的长度
float one = chaZhi / whatDuan;
List<float> points = new List<float>();
//首先增加第一个点
points.Add(formPoint);
//去掉首和尾值,只为取中间的值而循环,“这样能避免遇到例如 0.999999...这样的值后再循环执行” 的情况
int loopCount = whatPoint - 2;
for (int i = 1; i < loopCount + 1; i++)
{
points.Add(formPoint + (one * i));
}
//首先增加最后一个点
points.Add(toPoint);
return points;
}
测试:
结合着我的思路,我尝试将圆的直径平均分为100个点,然后将这个100个点的x值代入圆的标准方程,得到两个或一个y值,从而组合得到圆上的点的坐标,绘制的结果却不尽人意。好吧…这样从端点到中心点,圆上的点是越来越紧凑的,就好像是指数函数的增长形式,好吧涉及到我的知识盲区了…
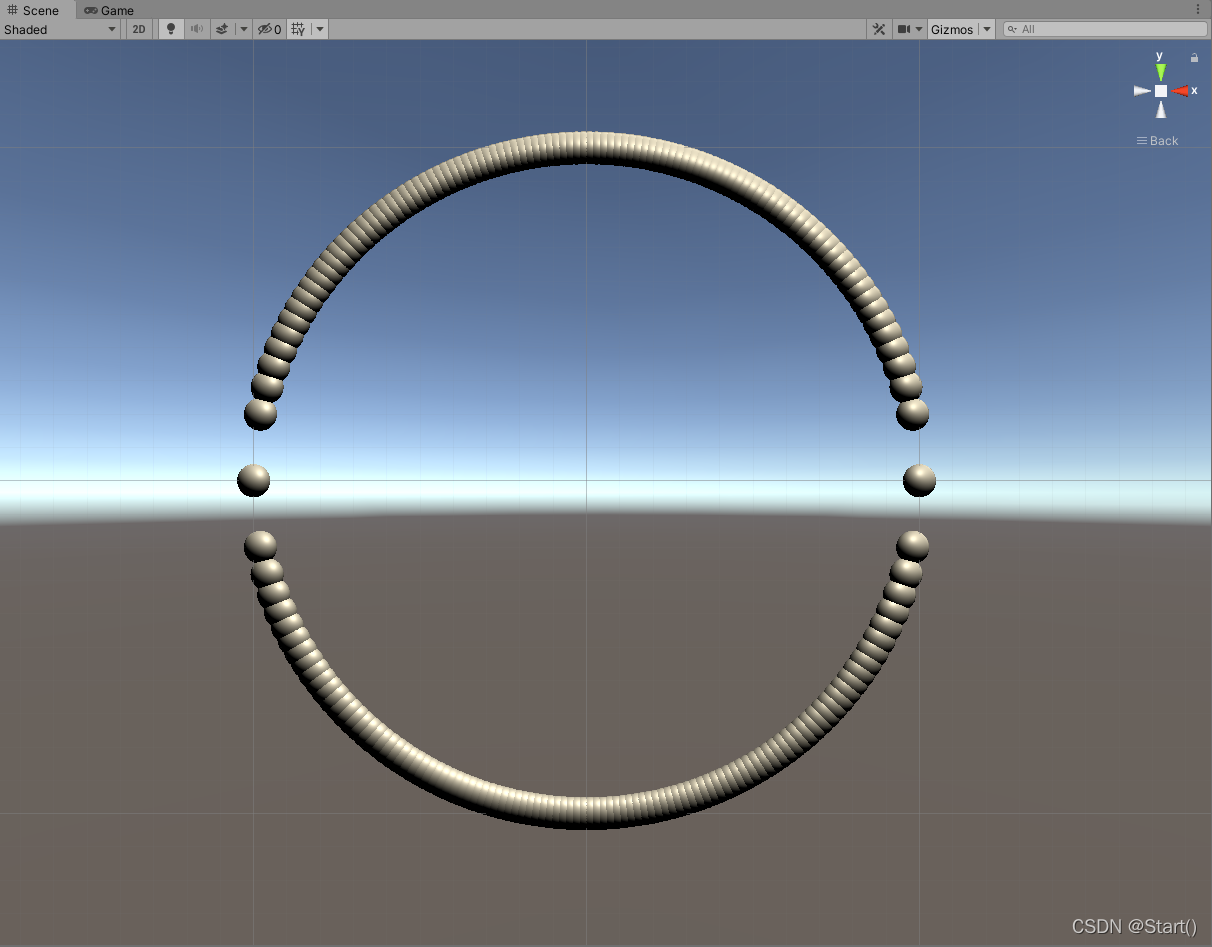
1000个呢?
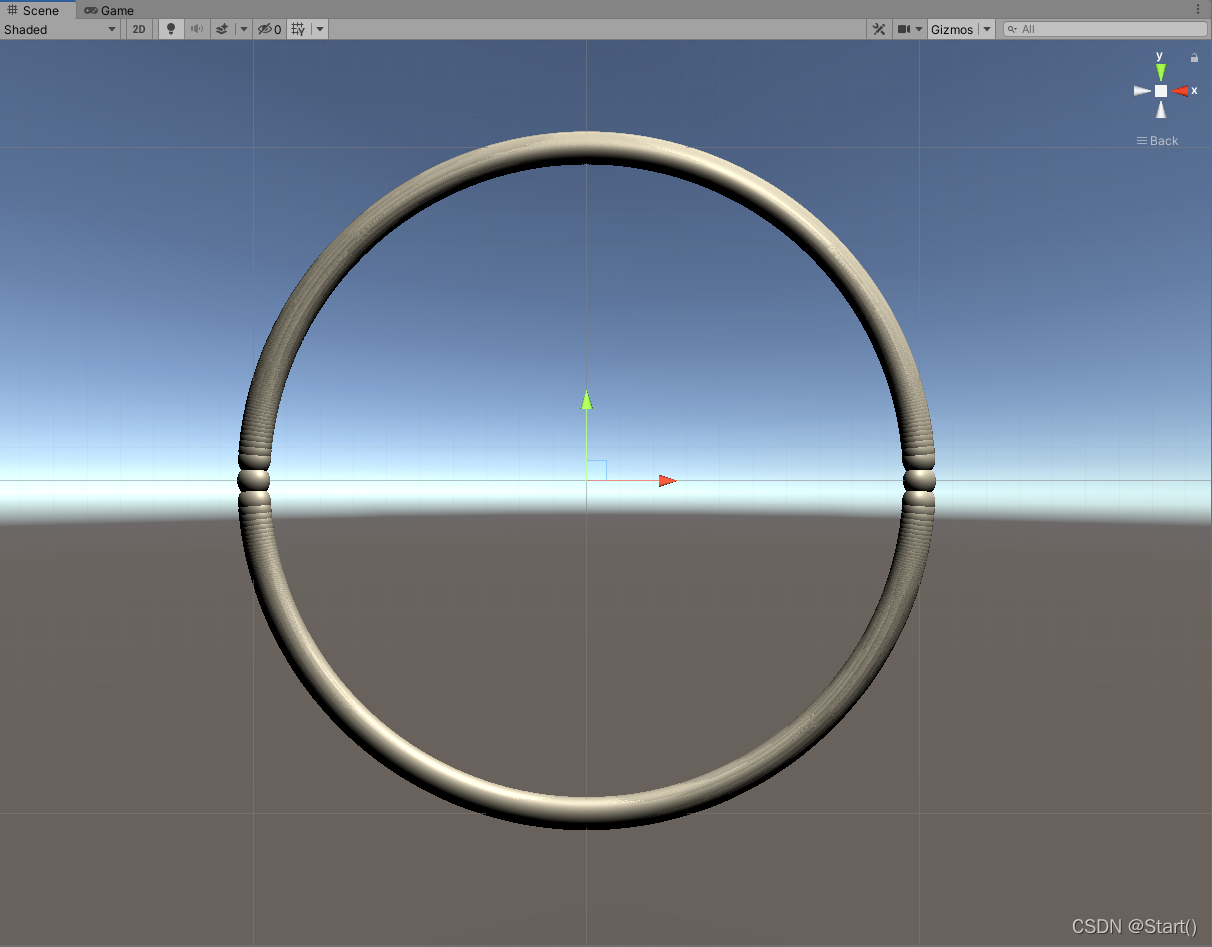
好不容易写到这里了,谁能想到是这个结果(T_T),端点到中心点的规律我也不懂,抱歉浪费了你生命中的几分钟…,作为补偿,我再使用另一种方法实现一下吧
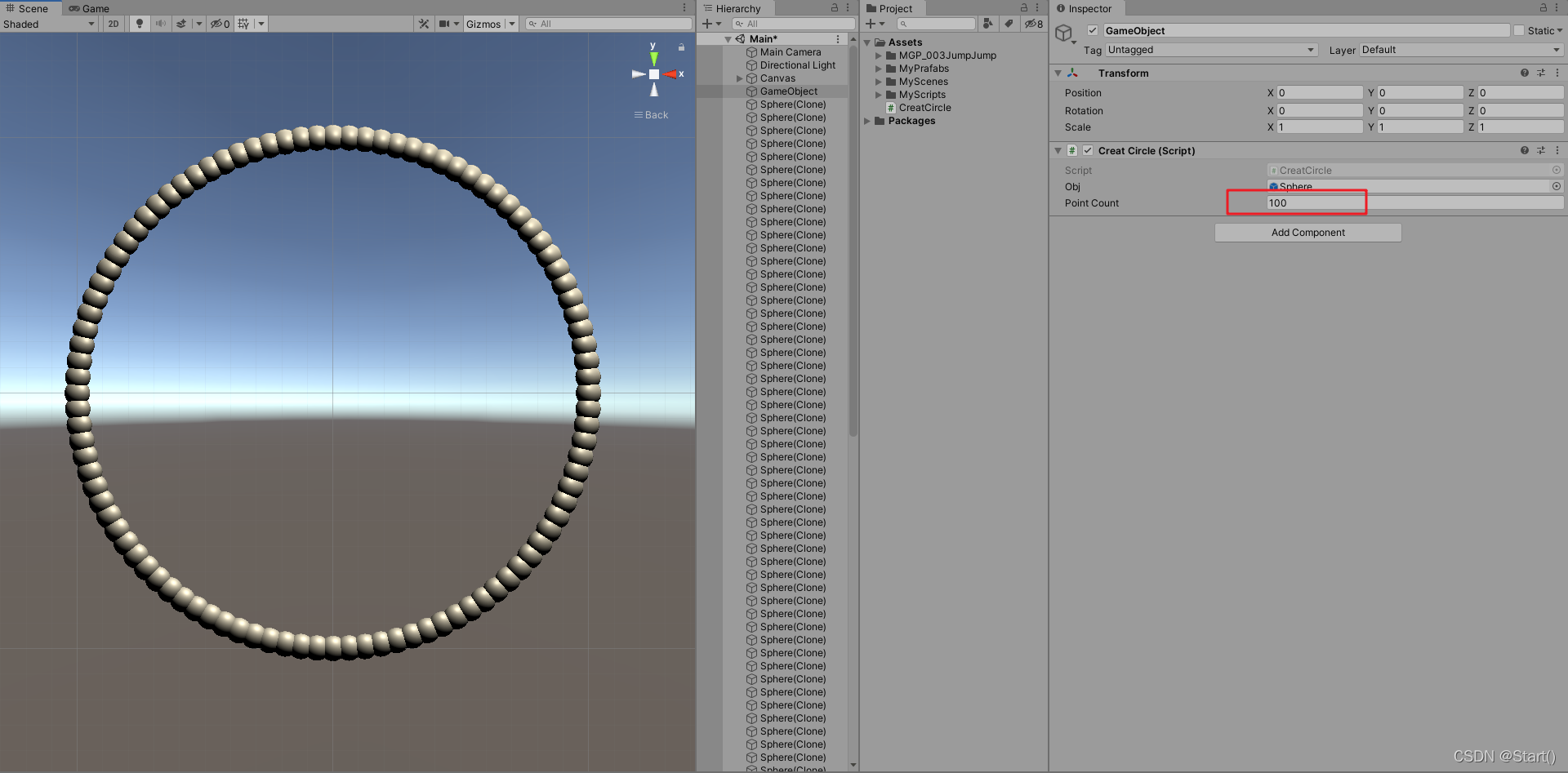
另一种方法的绘制思路是: 以圆心为起点、以半径为长度、在某角度上绘制向量,得到这个角度上向量的终点坐标,这样每隔一定度数绘制一个点,最后将点连起来就OK了,
参考了大佬的文章:已知起点坐标、角度、长度求终点坐标
完整代码:
using UnityEngine;
public class CreatCircle : MonoBehaviour
{
public GameObject obj;
public int pointCount = 12;//圆的点数
private void Start()
{
float perDu = 360f / pointCount;
int loopIndex = pointCount - 1;
if (obj)
{
for (int i = 0; i <= loopIndex; i++)
{
Vector2 v2 = GetEndPointByTrigonometric(i * perDu, Vector2.zero, 1f);
Instantiate(obj, v2, Quaternion.identity);
}
}
}
/// <summary>
/// 通过三角函数求终点坐标
/// </summary>
/// <param name="angle">角度</param>
/// <param name="startPoint">起点</param>
/// <param name="distance">距离</param>
/// <returns>终点坐标</returns>
public static Vector2 GetEndPointByTrigonometric(float angle, Vector2 startPoint, float distance)
{
Vector2 endPoint;
//角度转弧度
float radian = (angle * Mathf.PI) / 180;
//计算新坐标 r 就是两者的距离
endPoint.x = startPoint.x + distance * Mathf.Cos(radian);
endPoint.y = startPoint.y + distance * Mathf.Sin(radian);
return endPoint;
}
}
12个点:
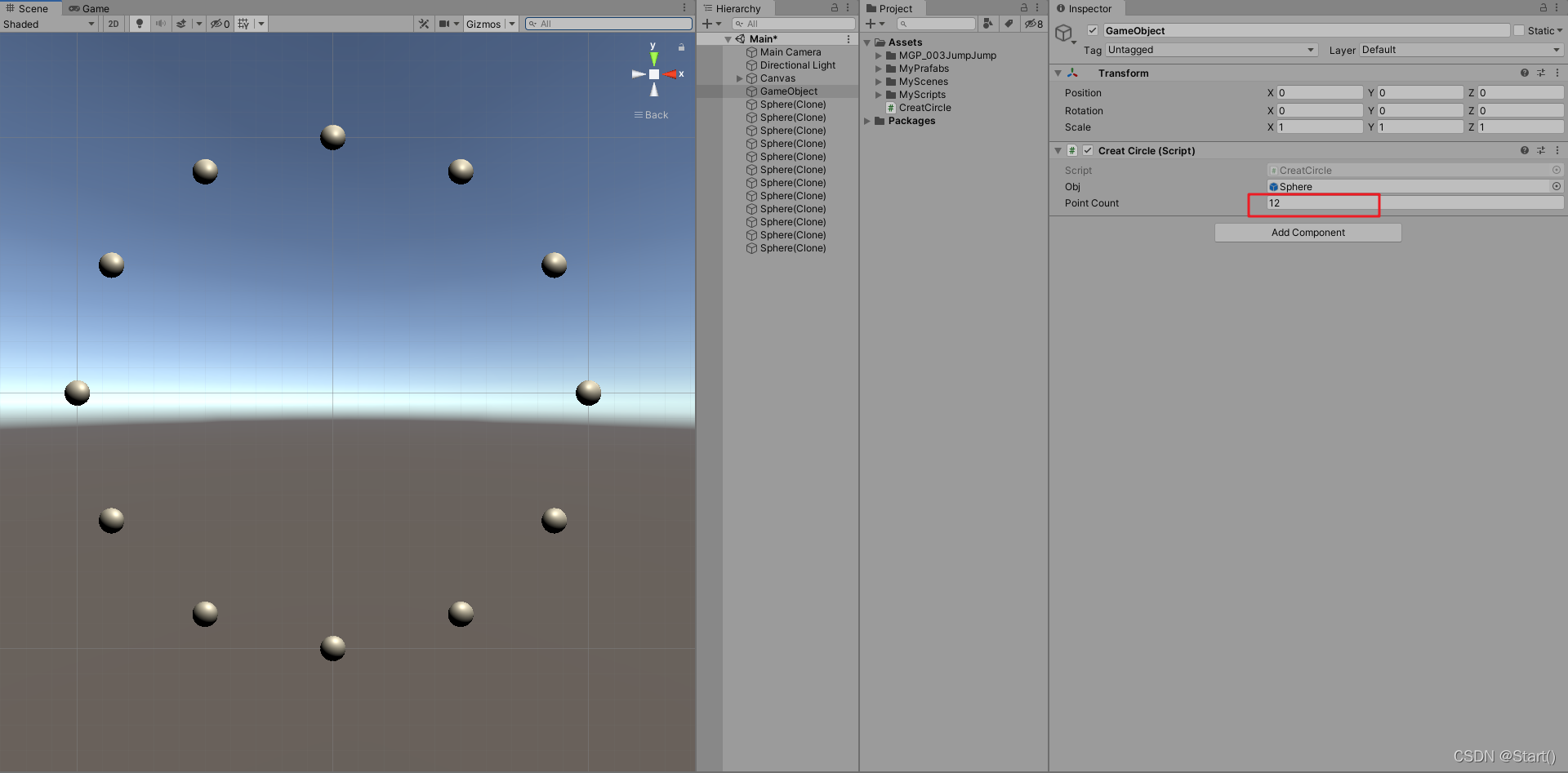
100个点: