1.引言
- 对于VRP类问题所给出的定义:
-背景条件:一组交通需求和一个车队
-任务:使用给定的车队,以最小的花销满足所有的(或部分的)交通需求。特别的是,决定车辆处理任务的顺序并保证所执行的车辆路径是可行的。
 - 车辆路径问题(Vehicle Routing problem, VRP):需要进行服务的点集中于某些特殊的点,因此区别于ARP。
2.The Capacitated Vehicle Routing Problem(CVRP)有能力约束的车辆路径问题
问题描述 Problem Statement
- 运输请求包括从单一的depot(节点0)运输至其他n个客户节点(N = {1,2,…,n})。
- 客户需求:qi ≥ 0, i ∈ N。
- 车队:一组在depot可使用的同质车辆K = {1,2,…,|K|},同质即具有相同的运输能力(Q > 0),并且相同的成本运行。
- 运输成本cij:车辆从i行驶至j的旅行费用。
- 将信息结构化为无向图或有向图G=(V,E)
-V={0}∪N={0,1,…,n}:即顶点,vertices (or nodes)
-无向图G=(V,E):即从i到j的cost不与方向相关,E={e={i,j}={j,i}:i,j∈V,i~=j},cost即cij for{i,j}∈E
-有向图G = (V,A):cij不等于cji(i,j∈ V)。A={(i,j)∈V×V:i~=j},cost即cij for(i,j)∈A
-|E| = n(n + 1)/2 and |A| = n(n + 1) ,都包含O(n^2)的连接 - route(or tour):顺序(i0,i1,i2,…,is,is+1),同时i0 =is+1 =0。-
-一辆车的行程包括客户点子集S ={i1,…,is}?N,cost and capacity constraint如下所示
 - 路径r1 , r2 , . . . , r|K|,与之相关的簇S1 , S2 , . . . , S|K|给CVRP提供了一个可行的解决方案(|K|个可行行程,one for each vehicle k ∈ K)
- 因此,CVRP包括两个不独立的任务:
(1)将客户集合N划分为可行的簇S1,…,S|K|;
(2)每辆车 k ∈ K的路径应该经由{0} ∪ Sk(等价于包含{0} ∪ Sk的TSP问题)
模型 Models
Basic Notation基本符号
- V: the set of nodes/vertices。S ? V
-无向图δ(S) = {{i, j} ∈ E : i ∈ S, j ∈/ S} (set E(S) = {{i, j} ∈ E : i, j ∈ S}边集)
-有向图:in-arcsδ?(S) = {(i, j) ∈ A: i ∈/ S, j ∈ S},out-arcsδ+(S) = {(i, j) ∈ A: i ∈ S, j ∈/ S}
-同时,A(S) = {(i, j) ∈ A: i, j ∈ S},包含S中所有可连接的顶点
-r(S):服务S的最小车辆数,通常使用[q(S)/q]代替。
Compact Formulations
- (VRP1)two vehicle-flow formulations
-决策变量:xij for{i,j}∈E(or (i,j)∈A)
1.1目标函数:最小化运输成本;
1.2保证每个节点只被访问一次
1.3车辆从depot出发数量
1.4子循环约束()
1.5决策变量约束
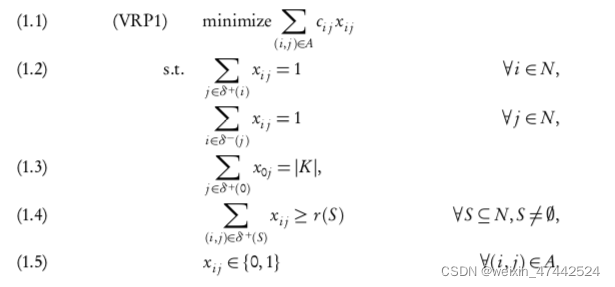

|