问题背景:brusselator模型
The Brusselator is a theoretical model for a type of autocatalytic reaction
brusselator模型是一种可以用来评估催化反应的理论模型
下面的资料来自wiki:
https://en.wikipedia.org/wiki/Brusselator
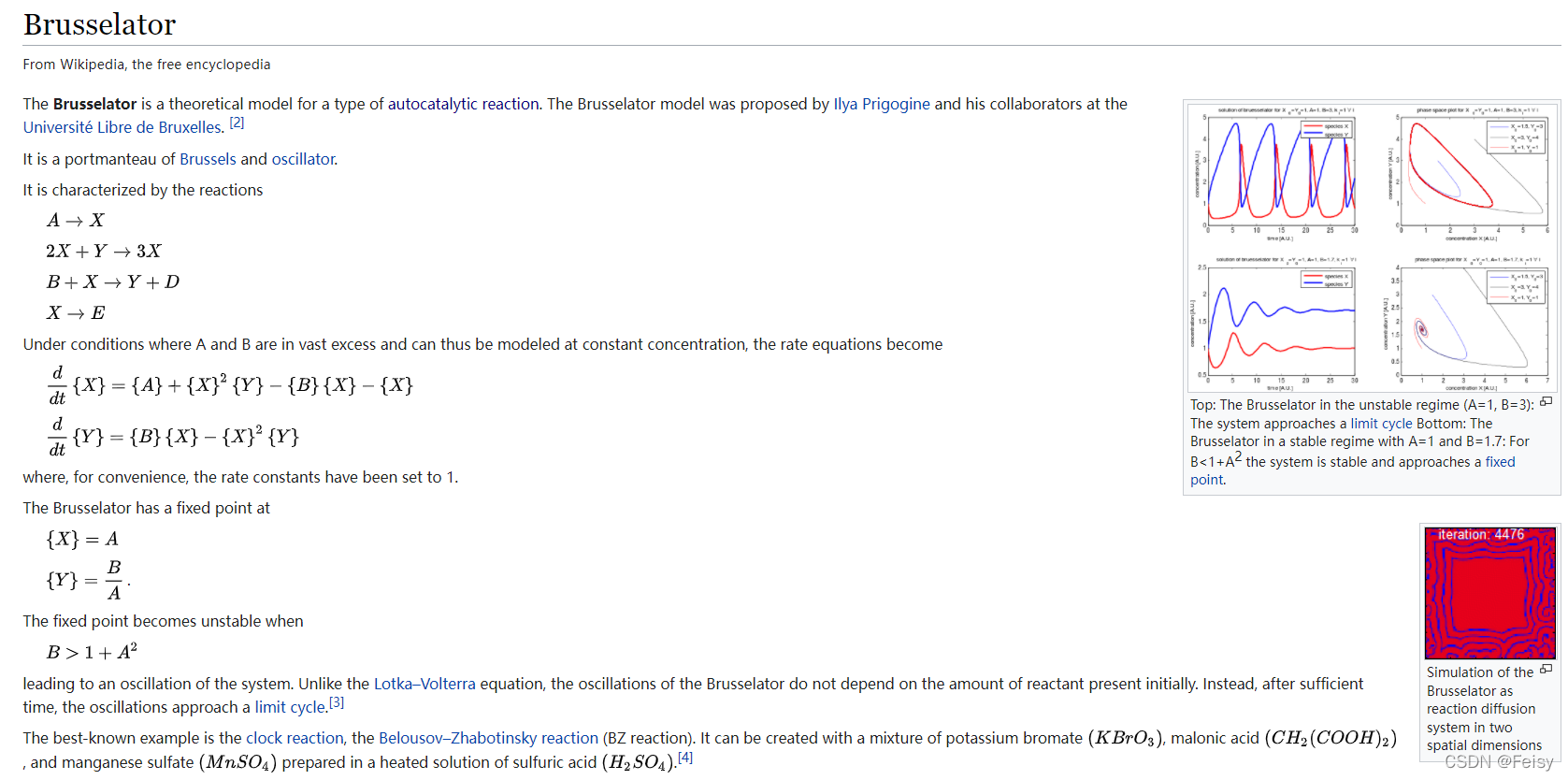
3D brusselator模型
假设有们有3D的brusselator模型,𝑌 = [𝑢, 𝑣, 𝑤],它的ODE方程如下:
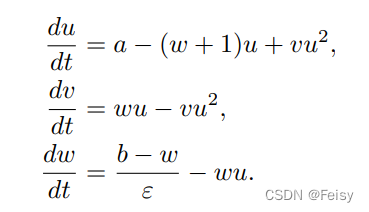
在不同的u0,v0,w0下,我们想对系统进行模拟,看 系统在[0,10]的时候,系统的轨迹
测试的3种初值条件:
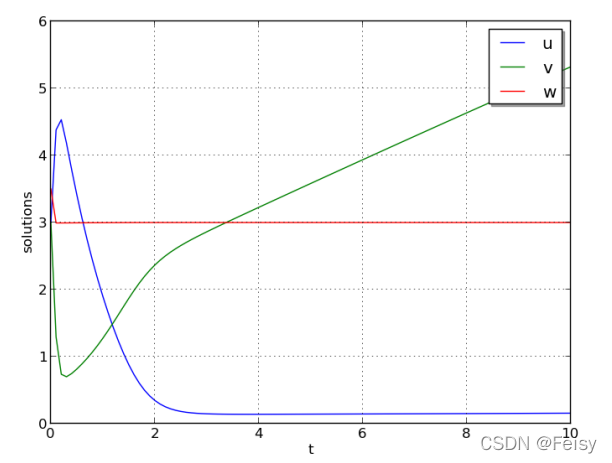
1 𝑢0 = 3.9, 𝑣0 = 1.1, 𝑤0 = 2.8, 𝑎 = 1.2, 𝑏 = 2.5, and 𝜀 = 10?5
all three components exhibit a rapid transient change during the first 0.2 time units, followed by a slow and smooth evolution
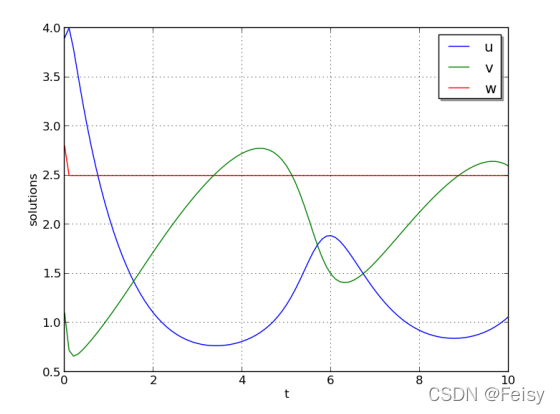
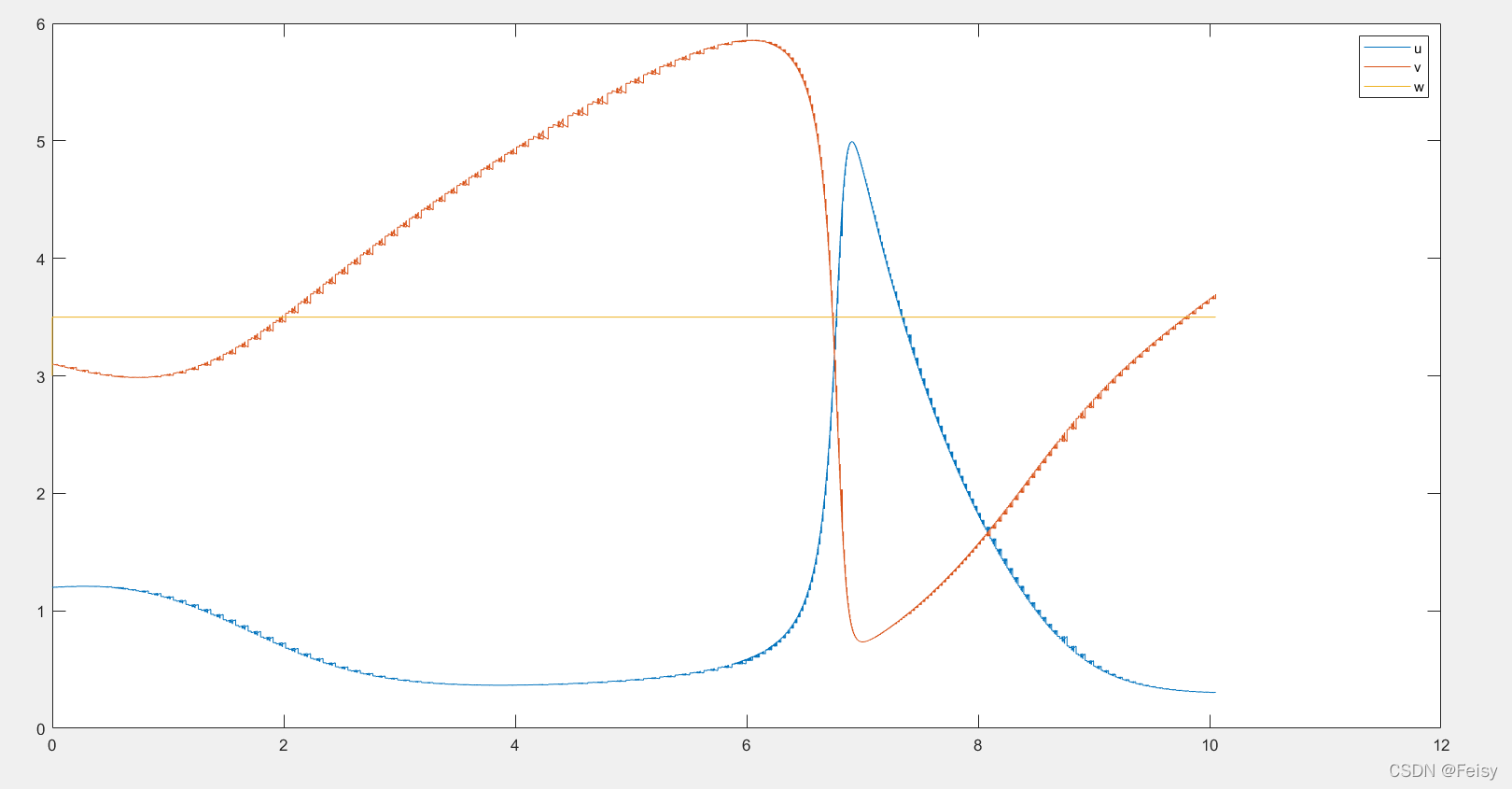
2 𝑢0 = 1.2, 𝑣0 = 3.1, 𝑤0 = 3, 𝑎 = 1, 𝑏 = 3.5, and 𝜀 = 5 · 10?6
, 𝑤 experiences a fast initial transient, jumping 0.5 within a few steps. All values proceed smoothly
until around 𝑡 = 6.5, when both 𝑢 and 𝑣 undergo a sharp transition, with 𝑢 increaseing from around 0.5 to 5 and 𝑣 decreasing from around 6 to 1 in less than 0.5 time units. After this transition, both 𝑢 and 𝑣 continue to evolve somewhat rapidly for another 1.4 time units, and finish off smoothly.
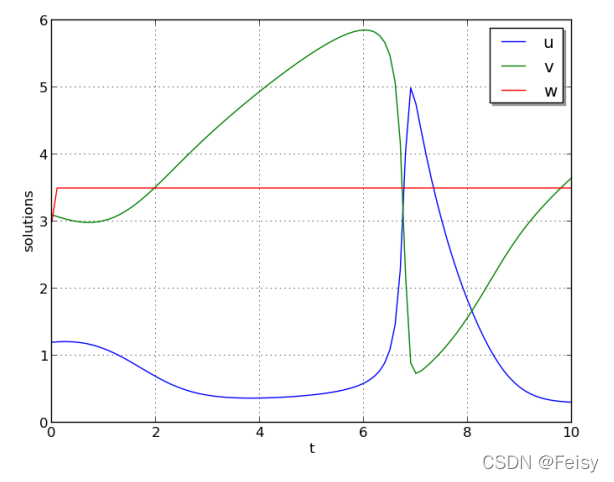
3 𝑢0 = 3, 𝑣0 = 3, 𝑤0 = 3.5, 𝑎 = 0.5, 𝑏 = 3, and 𝜀 = 5 · 10?4
Here, all components undergo very rapid initial transients during the first 0.3 time units, and all then proceed very smoothly for the remainder of the simulation.
diagonally-implicit Runge-Kutta methods:DIRK 方法的数值计算模拟
This program solves the problem with the DIRK method, using a Newton iteration with the SUNLINSOL_DENSE
linear solver module via the ARKDLS interface. Additionally, this example provides a routine to ARKDLS to compute
the dense Jacobian.
The problem is run using scalar relative and absolute tolerances of 𝑟𝑡𝑜𝑙 = 10?6
and 𝑎𝑡𝑜𝑙 = 10?10, respectively.
10 outputs are printed at equal intervals, and run statistics are printed at the end
1 实现代码
/*-----------------------------------------------------------------
* Programmer(s): Daniel R. Reynolds @ SMU
*---------------------------------------------------------------
* SUNDIALS Copyright Start
* Copyright (c) 2002-2021, Lawrence Livermore National Security
* and Southern Methodist University.
* All rights reserved.
*
* See the top-level LICENSE and NOTICE files for details.
*
* SPDX-License-Identifier: BSD-3-Clause
* SUNDIALS Copyright End
*---------------------------------------------------------------
* Example problem:
*
* The following test simulates a brusselator problem from chemical
* kinetics. This is an ODE system with 3 components, Y = [u,v,w],
* satisfying the equations,
* du/dt = a - (w+1)*u + v*u^2
* dv/dt = w*u - v*u^2
* dw/dt = (b-w)/ep - w*u
* for t in the interval [0.0, 10.0], with initial conditions
* Y0 = [u0,v0,w0].
*
* We have 3 different testing scenarios:
*
* Test 1: u0=3.9, v0=1.1, w0=2.8, a=1.2, b=2.5, ep=1.0e-5
* Here, all three components exhibit a rapid transient change
* during the first 0.2 time units, followed by a slow and
* smooth evolution.
*
* Test 2: u0=1.2, v0=3.1, w0=3, a=1, b=3.5, ep=5.0e-6
* Here, w experiences a fast initial transient, jumping 0.5
* within a few steps. All values proceed smoothly until
* around t=6.5, when both u and v undergo a sharp transition,
* with u increaseing from around 0.5 to 5 and v decreasing
* from around 6 to 1 in less than 0.5 time units. After this
* transition, both u and v continue to evolve somewhat
* rapidly for another 1.4 time units, and finish off smoothly.
*
* Test 3: u0=3, v0=3, w0=3.5, a=0.5, b=3, ep=5.0e-4
* Here, all components undergo very rapid initial transients
* during the first 0.3 time units, and all then proceed very
* smoothly for the remainder of the simulation.
*
* This file is hard-coded to use test 2.
*
* This program solves the problem with the DIRK method, using a
* Newton iteration with the SUNDENSE dense linear solver, and a
* user-supplied Jacobian routine.
*
* 100 outputs are printed at equal intervals, and run statistics
* are printed at the end.
*-----------------------------------------------------------------*/
/* Header files */
#include <stdio.h>
#include <math.h>
#include <arkode/arkode_arkstep.h> /* prototypes for ARKStep fcts., consts */
#include <nvector/nvector_serial.h> /* serial N_Vector types, fcts., macros */
#include <sunmatrix/sunmatrix_dense.h> /* access to dense SUNMatrix */
#include <sunlinsol/sunlinsol_dense.h> /* access to dense SUNLinearSolver */
#include <sundials/sundials_types.h> /* def. of type 'realtype' */
#include <unistd.h>
#include <time.h>
#include<string.h>
#include<sys/time.h>
#include <sys/timeb.h>
#include <stdio.h>
/*
* 获取系统时间
* added by xie shaoqin,2011-08-26
*/
long long GetMillsTime()
{
long long cur_time = 0;
struct timeval tp;
gettimeofday(&tp, NULL);
//必须将tp.tv_sec转成long long 再运算,这样子防止在32位机器上溢出
long long data = (long long) tp.tv_sec * 1000;
cur_time = data + tp.tv_usec / 1000;
return cur_time;
}
#if defined(SUNDIALS_EXTENDED_PRECISION)
#define GSYM "Lg"
#define ESYM "Le"
#define FSYM "Lf"
#else
#define GSYM "g"
#define ESYM "e"
#define FSYM "f"
#endif
/* User-supplied Functions Called by the Solver */
static int f(realtype t, N_Vector y, N_Vector ydot, void *user_data);
static int Jac(realtype t, N_Vector y, N_Vector fy, SUNMatrix J, void *user_data,
N_Vector tmp1, N_Vector tmp2, N_Vector tmp3);
/* Private function to check function return values */
static int check_flag(void *flagvalue, const char *funcname, int opt);
/* Main Program */
int main()
{
long long start_time = GetMillsTime();
/* general problem parameters */
realtype T0 = RCONST(0.0); /* initial time */
realtype Tf = RCONST(10.0); /* final time */
realtype dTout = RCONST(1.0); /* time between outputs */
sunindextype NEQ = 3; /* number of dependent vars. */
int Nt = (int) ceil(Tf/dTout); /* number of output times */
int test = 2; /* test problem to run */
realtype reltol = 1.0e-6; /* tolerances */
realtype abstol = 1.0e-10;
realtype a, b, ep, u0, v0, w0;
/* general problem variables */
int flag; /* reusable error-checking flag */
N_Vector y = NULL; /* empty vector for storing solution */
SUNMatrix A = NULL; /* empty matrix for solver */
SUNLinearSolver LS = NULL; /* empty linear solver object */
void *arkode_mem = NULL; /* empty ARKode memory structure */
realtype rdata[3];
FILE *UFID;
realtype t, tout;
int iout;
long int nst, nst_a, nfe, nfi, nsetups, nje, nfeLS, nni, ncfn, netf;
/* set up the test problem according to the desired test */
if (test == 1) {
u0 = RCONST(3.9);
v0 = RCONST(1.1);
w0 = RCONST(2.8);
a = RCONST(1.2);
b = RCONST(2.5);
ep = RCONST(1.0e-5);
} else if (test == 3) {
u0 = RCONST(3.0);
v0 = RCONST(3.0);
w0 = RCONST(3.5);
a = RCONST(0.5);
b = RCONST(3.0);
ep = RCONST(5.0e-4);
} else {
u0 = RCONST(1.2);
v0 = RCONST(3.1);
w0 = RCONST(3.0);
a = RCONST(1.0);
b = RCONST(3.5);
ep = RCONST(5.0e-6);
}
/* Initial problem output */
printf("\nBrusselator ODE test problem:\n");
printf(" initial conditions: u0 = %"GSYM", v0 = %"GSYM", w0 = %"GSYM"\n",u0,v0,w0);
printf(" problem parameters: a = %"GSYM", b = %"GSYM", ep = %"GSYM"\n",a,b,ep);
printf(" reltol = %.1"ESYM", abstol = %.1"ESYM"\n\n",reltol,abstol);
/* Initialize data structures */
rdata[0] = a; /* set user data */
rdata[1] = b;
rdata[2] = ep;
y = N_VNew_Serial(NEQ); /* Create serial vector for solution */
if (check_flag((void *)y, "N_VNew_Serial", 0)) return 1;
NV_Ith_S(y,0) = u0; /* Set initial conditions */
NV_Ith_S(y,1) = v0;
NV_Ith_S(y,2) = w0;
/* Call ARKStepCreate to initialize the ARK timestepper module and
specify the right-hand side function in y'=f(t,y), the inital time
T0, and the initial dependent variable vector y. Note: since this
problem is fully implicit, we set f_E to NULL and f_I to f. */
arkode_mem = ARKStepCreate(NULL, f, T0, y);
if (check_flag((void *)arkode_mem, "ARKStepCreate", 0)) return 1;
/* Set routines */
flag = ARKStepSetUserData(arkode_mem, (void *) rdata); /* Pass rdata to user functions */
if (check_flag(&flag, "ARKStepSetUserData", 1)) return 1;
flag = ARKStepSStolerances(arkode_mem, reltol, abstol); /* Specify tolerances */
if (check_flag(&flag, "ARKStepSStolerances", 1)) return 1;
flag = ARKStepSetInterpolantType(arkode_mem, ARK_INTERP_LAGRANGE); /* Specify stiff interpolant */
if (check_flag(&flag, "ARKStepSetInterpolantType", 1)) return 1;
/* Initialize dense matrix data structure and solver */
A = SUNDenseMatrix(NEQ, NEQ);
if (check_flag((void *)A, "SUNDenseMatrix", 0)) return 1;
LS = SUNLinSol_Dense(y, A);
if (check_flag((void *)LS, "SUNLinSol_Dense", 0)) return 1;
/* Linear solver interface */
flag = ARKStepSetLinearSolver(arkode_mem, LS, A); /* Attach matrix and linear solver */
if (check_flag(&flag, "ARKStepSetLinearSolver", 1)) return 1;
flag = ARKStepSetJacFn(arkode_mem, Jac); /* Set Jacobian routine */
if (check_flag(&flag, "ARKStepSetJacFn", 1)) return 1;
/* Open output stream for results, output comment line */
UFID = fopen("solution.txt","w");
fprintf(UFID,"# t u v w\n");
/* output initial condition to disk */
fprintf(UFID," %.16"ESYM" %.16"ESYM" %.16"ESYM" %.16"ESYM"\n",
T0, NV_Ith_S(y,0), NV_Ith_S(y,1), NV_Ith_S(y,2));
/* Main time-stepping loop: calls ARKStepEvolve to perform the integration, then
prints results. Stops when the final time has been reached */
t = T0;
tout = T0+dTout;
printf(" t u v w\n");
printf(" -------------------------------------------\n");
printf(" %10.6"FSYM" %10.6"FSYM" %10.6"FSYM" %10.6"FSYM"\n",
t, NV_Ith_S(y,0), NV_Ith_S(y,1), NV_Ith_S(y,2));
for (iout=0; iout<Nt; iout++) {
flag = ARKStepEvolve(arkode_mem, tout, y, &t, ARK_NORMAL); /* call integrator */
if (check_flag(&flag, "ARKStepEvolve", 1)) break;
printf(" %10.6"FSYM" %10.6"FSYM" %10.6"FSYM" %10.6"FSYM"\n", /* access/print solution */
t, NV_Ith_S(y,0), NV_Ith_S(y,1), NV_Ith_S(y,2));
fprintf(UFID," %.16"ESYM" %.16"ESYM" %.16"ESYM" %.16"ESYM"\n",
t, NV_Ith_S(y,0), NV_Ith_S(y,1), NV_Ith_S(y,2));
if (flag >= 0) { /* successful solve: update time */
tout += dTout;
tout = (tout > Tf) ? Tf : tout;
} else { /* unsuccessful solve: break */
fprintf(stderr,"Solver failure, stopping integration\n");
break;
}
}
printf(" -------------------------------------------\n");
fclose(UFID);
/* Print some final statistics */
flag = ARKStepGetNumSteps(arkode_mem, &nst);
check_flag(&flag, "ARKStepGetNumSteps", 1);
flag = ARKStepGetNumStepAttempts(arkode_mem, &nst_a);
check_flag(&flag, "ARKStepGetNumStepAttempts", 1);
flag = ARKStepGetNumRhsEvals(arkode_mem, &nfe, &nfi);
check_flag(&flag, "ARKStepGetNumRhsEvals", 1);
flag = ARKStepGetNumLinSolvSetups(arkode_mem, &nsetups);
check_flag(&flag, "ARKStepGetNumLinSolvSetups", 1);
flag = ARKStepGetNumErrTestFails(arkode_mem, &netf);
check_flag(&flag, "ARKStepGetNumErrTestFails", 1);
flag = ARKStepGetNumNonlinSolvIters(arkode_mem, &nni);
check_flag(&flag, "ARKStepGetNumNonlinSolvIters", 1);
flag = ARKStepGetNumNonlinSolvConvFails(arkode_mem, &ncfn);
check_flag(&flag, "ARKStepGetNumNonlinSolvConvFails", 1);
flag = ARKStepGetNumJacEvals(arkode_mem, &nje);
check_flag(&flag, "ARKStepGetNumJacEvals", 1);
flag = ARKStepGetNumLinRhsEvals(arkode_mem, &nfeLS);
check_flag(&flag, "ARKStepGetNumLinRhsEvals", 1);
printf("\nFinal Solver Statistics:\n");
printf(" Internal solver steps = %li (attempted = %li)\n", nst, nst_a);
printf(" Total RHS evals: Fe = %li, Fi = %li\n", nfe, nfi);
printf(" Total linear solver setups = %li\n", nsetups);
printf(" Total RHS evals for setting up the linear system = %li\n", nfeLS);
printf(" Total number of Jacobian evaluations = %li\n", nje);
printf(" Total number of Newton iterations = %li\n", nni);
printf(" Total number of linear solver convergence failures = %li\n", ncfn);
printf(" Total number of error test failures = %li\n\n", netf);
/* Clean up and return with successful completion */
N_VDestroy(y); /* Free y vector */
ARKStepFree(&arkode_mem); /* Free integrator memory */
SUNLinSolFree(LS); /* Free linear solver */
SUNMatDestroy(A); /* Free A matrix */
long long end_time = GetMillsTime();
long long use_time = end_time - start_time;
printf("use time = %lld\n",use_time);
return 0;
}
/*-------------------------------
* Functions called by the solver
*-------------------------------*/
/* f routine to compute the ODE RHS function f(t,y). */
static int f(realtype t, N_Vector y, N_Vector ydot, void *user_data)
{
realtype *rdata = (realtype *) user_data; /* cast user_data to realtype */
realtype a = rdata[0]; /* access data entries */
realtype b = rdata[1];
realtype ep = rdata[2];
realtype u = NV_Ith_S(y,0); /* access solution values */
realtype v = NV_Ith_S(y,1);
realtype w = NV_Ith_S(y,2);
/* fill in the RHS function */
NV_Ith_S(ydot,0) = a - (w+1.0)*u + v*u*u;
NV_Ith_S(ydot,1) = w*u - v*u*u;
NV_Ith_S(ydot,2) = (b-w)/ep - w*u;
return 0; /* Return with success */
}
/* Jacobian routine to compute J(t,y) = df/dy. */
static int Jac(realtype t, N_Vector y, N_Vector fy, SUNMatrix J, void *user_data,
N_Vector tmp1, N_Vector tmp2, N_Vector tmp3)
{
realtype *rdata = (realtype *) user_data; /* cast user_data to realtype */
realtype ep = rdata[2]; /* access data entries */
realtype u = NV_Ith_S(y,0); /* access solution values */
realtype v = NV_Ith_S(y,1);
realtype w = NV_Ith_S(y,2);
/* fill in the Jacobian via SUNDenseMatrix macro, SM_ELEMENT_D (see sunmatrix_dense.h) */
SM_ELEMENT_D(J,0,0) = -(w+1.0) + 2.0*u*v;
SM_ELEMENT_D(J,0,1) = u*u;
SM_ELEMENT_D(J,0,2) = -u;
SM_ELEMENT_D(J,1,0) = w - 2.0*u*v;
SM_ELEMENT_D(J,1,1) = -u*u;
SM_ELEMENT_D(J,1,2) = u;
SM_ELEMENT_D(J,2,0) = -w;
SM_ELEMENT_D(J,2,1) = 0.0;
SM_ELEMENT_D(J,2,2) = -1.0/ep - u;
return 0; /* Return with success */
}
/*-------------------------------
* Private helper functions
*-------------------------------*/
/* Check function return value...
opt == 0 means SUNDIALS function allocates memory so check if
returned NULL pointer
opt == 1 means SUNDIALS function returns a flag so check if
flag >= 0
opt == 2 means function allocates memory so check if returned
NULL pointer
*/
static int check_flag(void *flagvalue, const char *funcname, int opt)
{
int *errflag;
/* Check if SUNDIALS function returned NULL pointer - no memory allocated */
if (opt == 0 && flagvalue == NULL) {
fprintf(stderr, "\nSUNDIALS_ERROR: %s() failed - returned NULL pointer\n\n",
funcname);
return 1; }
/* Check if flag < 0 */
else if (opt == 1) {
errflag = (int *) flagvalue;
if (*errflag < 0) {
fprintf(stderr, "\nSUNDIALS_ERROR: %s() failed with flag = %d\n\n",
funcname, *errflag);
return 1; }}
/* Check if function returned NULL pointer - no memory allocated */
else if (opt == 2 && flagvalue == NULL) {
fprintf(stderr, "\nMEMORY_ERROR: %s() failed - returned NULL pointer\n\n",
funcname);
return 1; }
return 0;
}
/*---- end of file ----*/
需要注意的是,计算的时间在10ms内,初始化用掉的时间几乎是20ms
2 测试结果1
采用初值的方案2 ,𝑟𝑡𝑜𝑙 = 10?6 and 𝑎𝑡𝑜𝑙 = 10?10,提供JAC的条件下
计算了4618次,用了15ms
Brusselator ODE test problem:
initial conditions: u0 = 1.2, v0 = 3.1, w0 = 3
problem parameters: a = 1, b = 3.5, ep = 5e-06
reltol = 1.0e-06, abstol = 1.0e-10
t u v w
-------------------------------------------
0.000000 1.200000 3.100000 3.000000
1.000000 1.103855 3.013156 3.499981
2.000000 0.687994 3.521381 3.499988
3.000000 0.409466 4.277885 3.499993
4.000000 0.367887 4.942004 3.499994
5.000000 0.413859 5.510617 3.499993
6.000000 0.589236 5.855675 3.499990
7.000000 4.756553 0.735408 3.499917
8.000000 1.813439 1.575779 3.499968
9.000000 0.527896 2.807370 3.499991
10.000000 0.305599 3.657381 3.499995
-------------------------------------------
Final Solver Statistics:
Internal solver steps = 251 (attempted = 253)
Total RHS evals: Fe = 0, Fi = 4618
Total linear solver setups = 97
Total RHS evals for setting up the linear system = 0
Total number of Jacobian evaluations = 67
Total number of Newton iterations = 3354
Total number of linear solver convergence failures = 1
Total number of error test failures = 1
use time = 32,calc [4618] times
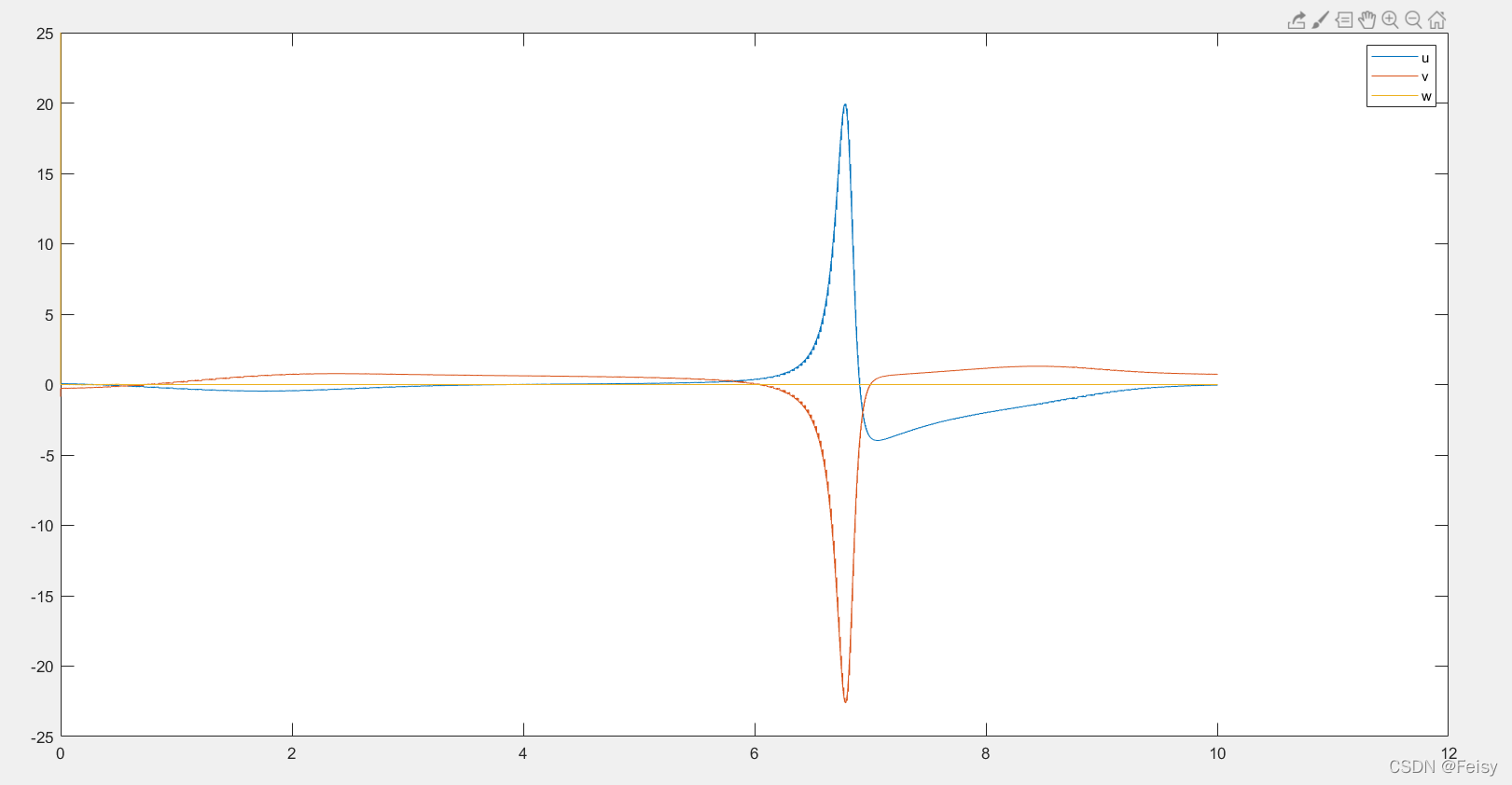
数据中需要注意的是dw的值:一开始dw的值十分巨大,随后迅速下降至靠近0,之后一直在0附近波动
数据格式是:t,du,dv,dw
0.000000,0.664000,-0.864000,99996.400000;
0.000000,0.663969,-0.863969,99991.238122;
0.000000,0.661265,-0.861265,99540.497829;
0.000000,0.664000,-0.864000,99996.400000;
0.000000,0.663658,-0.863658,99939.444687;
0.000000,0.663658,-0.863658,99939.444687;
…
0.000060,0.064022,-0.264029,0.638044;
0.000064,0.064024,-0.264031,0.888462;
0.000064,0.064019,-0.264026,0.278371;
0.000063,0.064024,-0.264031,0.888462;
0.000063,0.064020,-0.264027,0.406020;
u,v,w曲线图
du,dv,dw曲线图
3 测试结果2 改大atol,rtol
Brusselator ODE test problem:
initial conditions: u0 = 1.2, v0 = 3.1, w0 = 3
problem parameters: a = 1, b = 3.5, ep = 5e-06
reltol = 1.0e-02, abstol = 1.0e-02
t u v w
-------------------------------------------
0.000000 1.200000 3.100000 3.000000
1.000000 1.105760 3.008656 3.499351
2.000000 0.687951 3.517377 3.499988
3.000000 0.408339 4.274325 3.499993
4.000000 0.369702 4.939621 3.499994
5.000000 0.414450 5.507015 3.499993
6.000000 0.587880 5.856210 3.499990
7.000000 4.803068 0.732940 3.499916
8.000000 1.817444 1.578584 3.499967
9.000000 0.538093 2.796798 3.499991
10.000000 0.305386 3.652488 3.499995
use time = 3,calc [662] times
-------------------------------------------
Final Solver Statistics:
Internal solver steps = 43 (attempted = 48)
Total RHS evals: Fe = 0, Fi = 662
Total linear solver setups = 41
Total RHS evals for setting up the linear system = 0
Total number of Jacobian evaluations = 20
Total number of Newton iterations = 439
Total number of linear solver convergence failures = 5
Total number of error test failures = 0
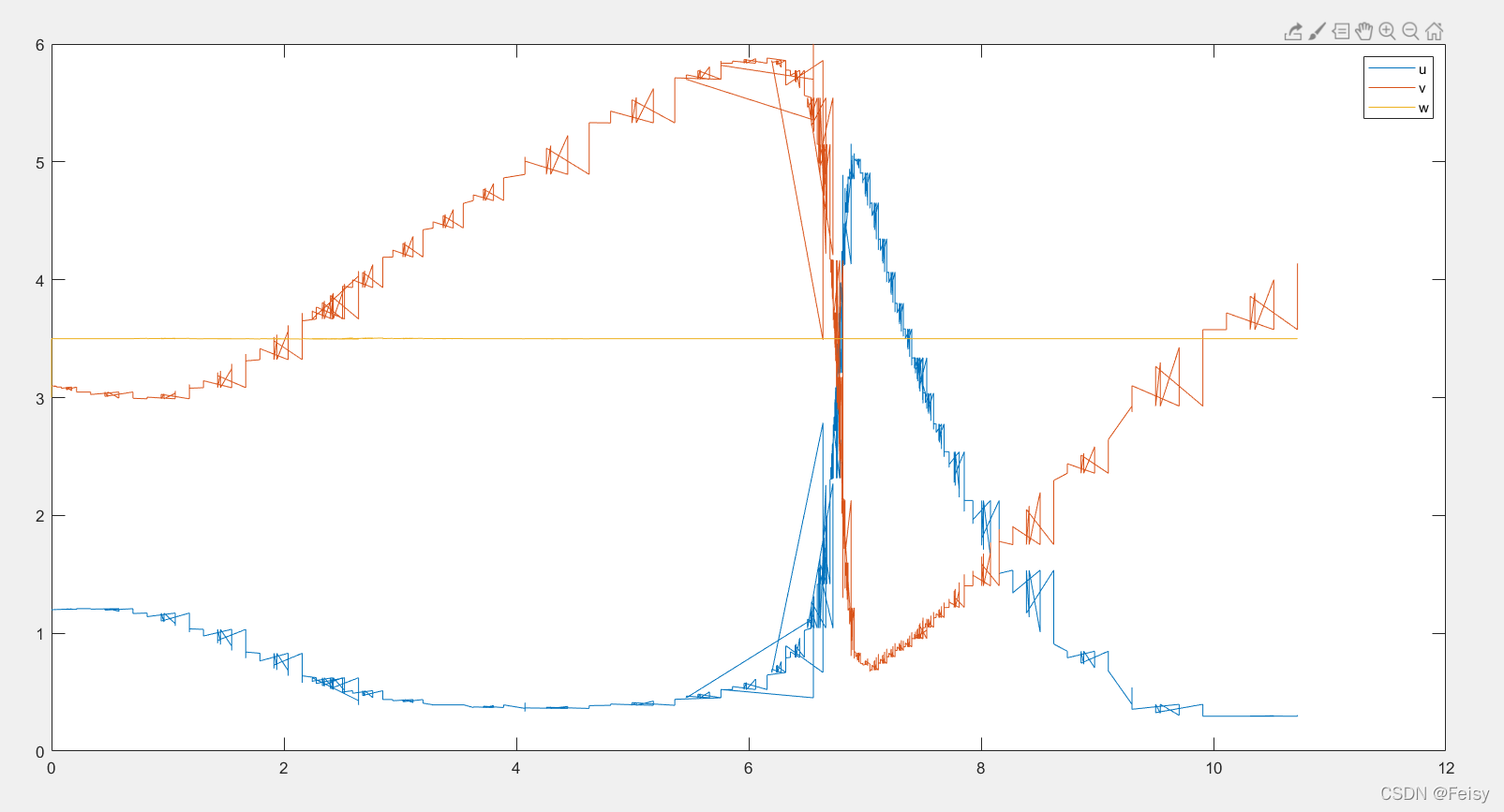
采用初值的方案2 ,𝑟𝑡𝑜𝑙 = 10?2 and 𝑎𝑡𝑜𝑙 = 10?2,提供JAC的条件下
计算了662次,用了3 ms,波形跟测试1相比,u,v,w明显在局部范围的的波动更大,但是整体走向还可以
u,v,w曲线图
du,dv,dw曲线图
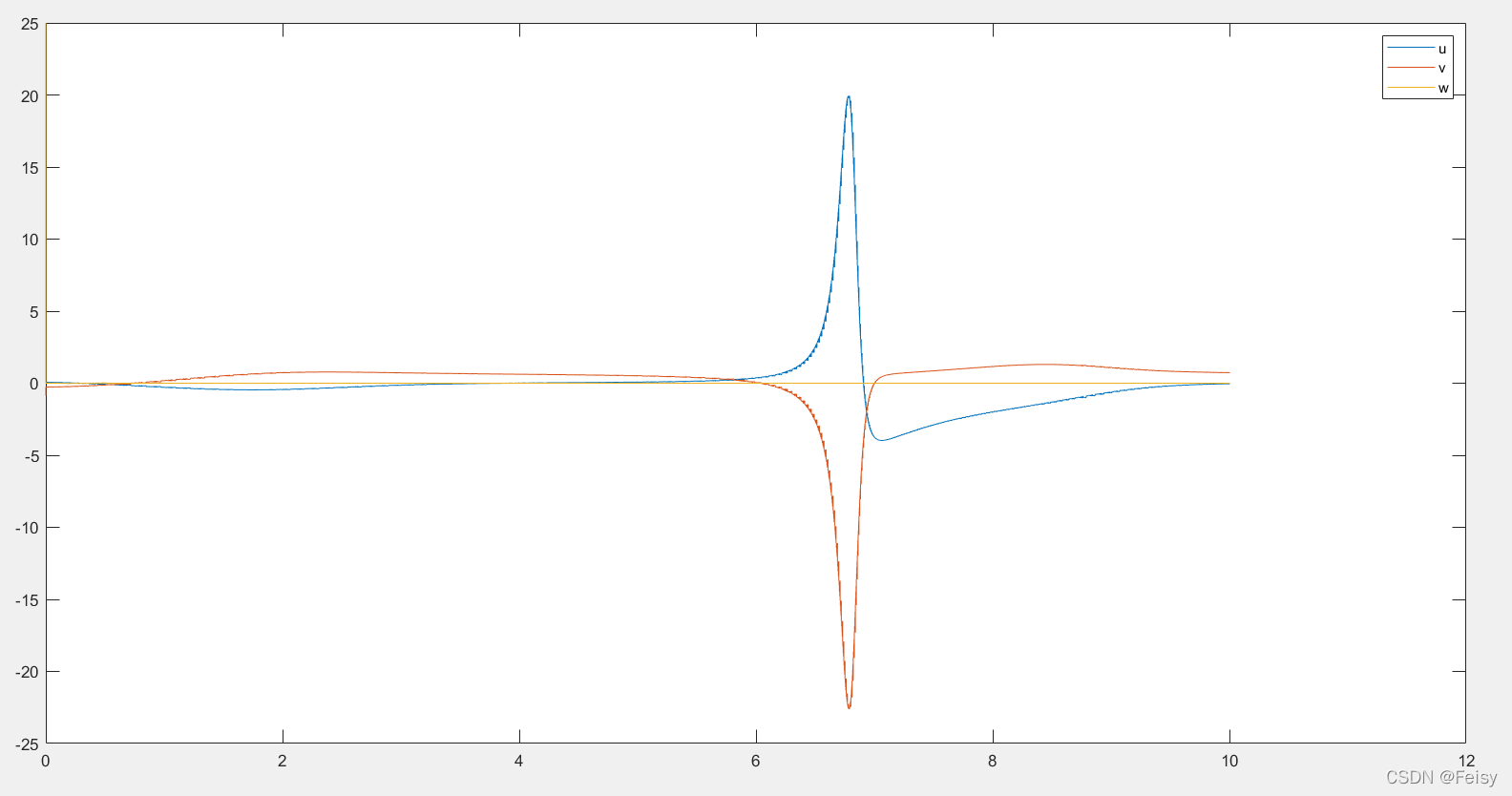
4 测试结果3 移除Jac
采用初值的方案2 ,𝑟𝑡𝑜𝑙 = 10?2 and 𝑎𝑡𝑜𝑙 = 10?2,不提供JAC的条件下
计算了732次,用了3 ms,波形跟测试2相比, 没有太明显的差异
Brusselator ODE test problem:
initial conditions: u0 = 1.2, v0 = 3.1, w0 = 3
problem parameters: a = 1, b = 3.5, ep = 5e-06
reltol = 1.0e-02, abstol = 1.0e-02
t u v w
-------------------------------------------
0.000000 1.200000 3.100000 3.000000
1.000000 1.105756 3.008666 3.499365
2.000000 0.687951 3.517384 3.499988
3.000000 0.408333 4.274329 3.499993
4.000000 0.369701 4.939627 3.499994
5.000000 0.414455 5.507020 3.499993
6.000000 0.587895 5.856193 3.499990
7.000000 4.802629 0.732841 3.499916
8.000000 1.816917 1.578595 3.499967
9.000000 0.539045 2.796289 3.499991
10.000000 0.306481 3.652372 3.499995
use time = 3,calc [732] times
-------------------------------------------
Final Solver Statistics:
Internal solver steps = 43 (attempted = 48)
Total RHS evals: Fe = 0, Fi = 669
Total linear solver setups = 42
Total RHS evals for setting up the linear system = 63
Total number of Jacobian evaluations = 21
Total number of Newton iterations = 446
Total number of linear solver convergence failures = 5
Total number of error test failures = 0
由此可见,没有Jac,计算效率会下降一部分
u,v,w曲线图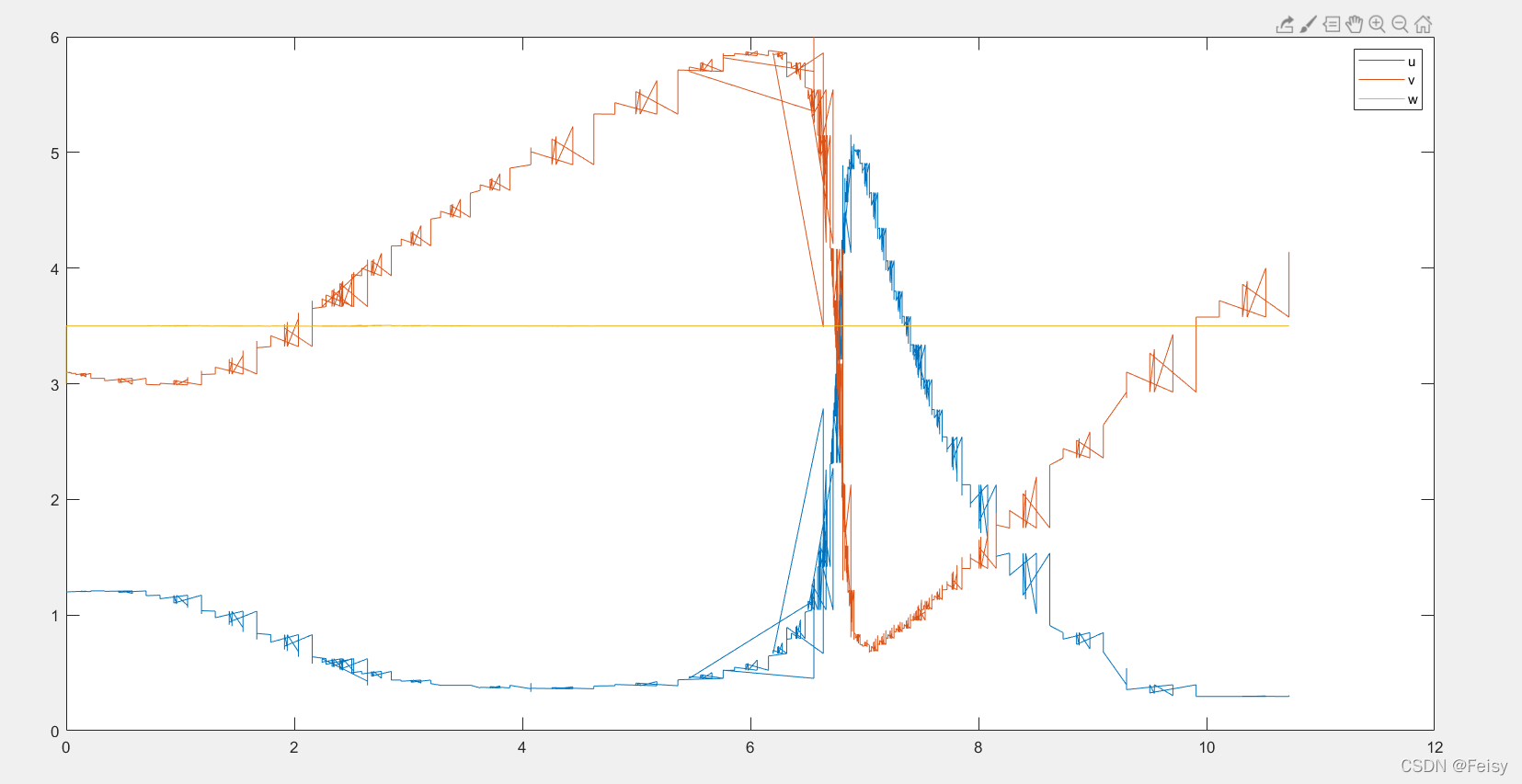
du,dv,dw曲线图
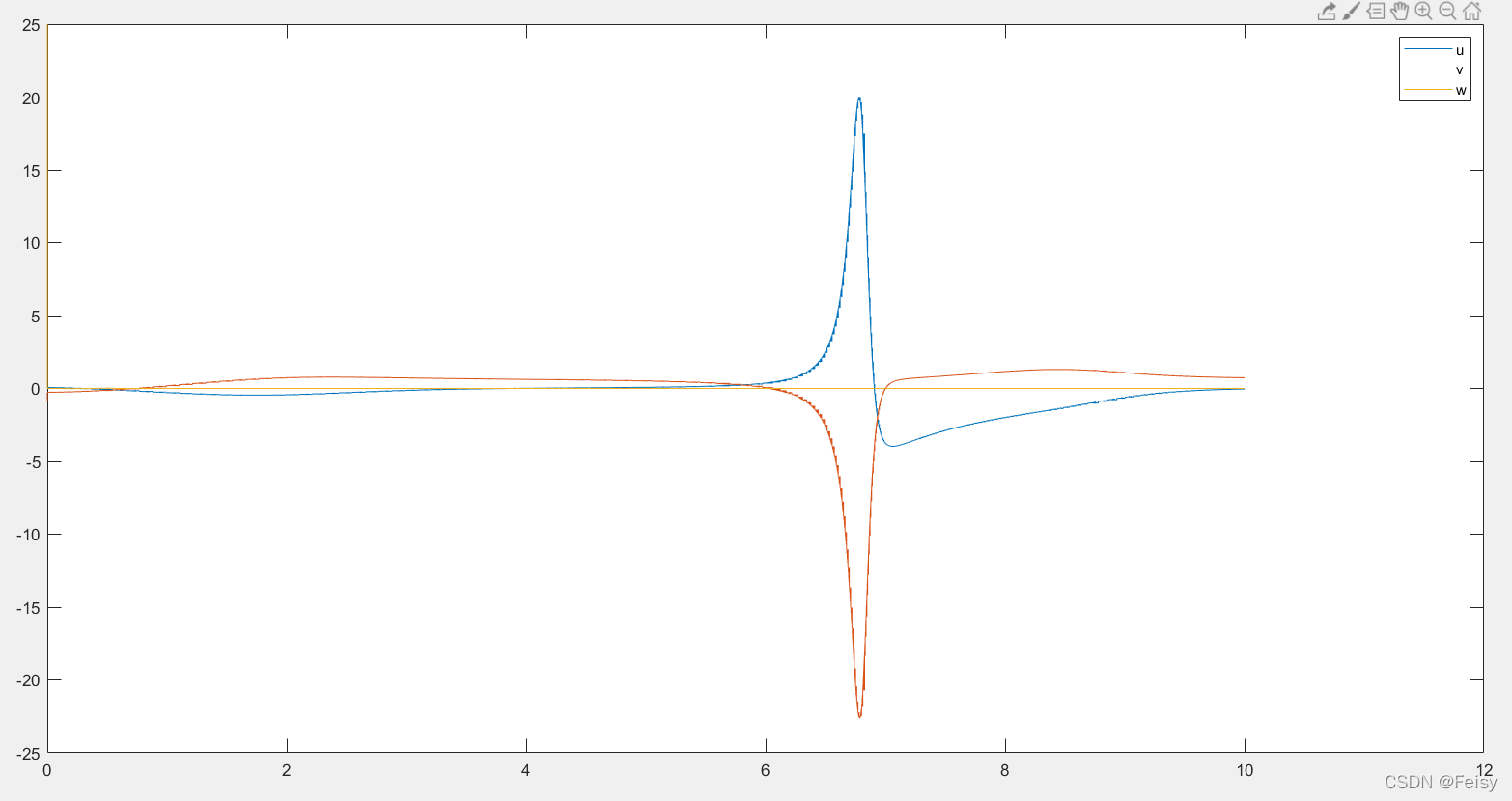
5 测试结果4:Lagrange VS Hermite 积分
按照
Hermite积分法
Lagrange 积分法
所说,Hermite适合nostiff问题,Lagrange 适合stiff问题
但是这里测试,没有测试出区别,可能是模型的原因。
Brusselator ODE test problem:
initial conditions: u0 = 1.2, v0 = 3.1, w0 = 3
problem parameters: a = 1, b = 3.5, ep = 5e-06
reltol = 1.0e-02, abstol = 1.0e-02
t u v w
-------------------------------------------
0.000000 1.200000 3.100000 3.000000
1.000000 1.105955 3.008757 3.500472
2.000000 0.687940 3.517329 3.499989
3.000000 0.394811 4.290552 3.499994
4.000000 0.369418 4.945967 3.499994
5.000000 0.415174 5.506758 3.499993
6.000000 0.590300 5.853072 3.499990
7.000000 4.801918 0.733504 3.499916
8.000000 1.813978 1.580666 3.499968
9.000000 0.530698 2.803104 3.499991
10.000000 0.310003 3.650727 3.499995
use time = 2,calc [732] times
-------------------------------------------
Final Solver Statistics:
Internal solver steps = 43 (attempted = 48)
Total RHS evals: Fe = 0, Fi = 669
Total linear solver setups = 42
Total RHS evals for setting up the linear system = 63
Total number of Jacobian evaluations = 21
Total number of Newton iterations = 446
Total number of linear solver convergence failures = 5
Total number of error test failures = 0
6 测试结果5:使用非线性fixed-point求解器
将原始问题拆分成stiff,nonstiff两部分
- stiff:因为 ? \epsilon ?是量级很小, ? \epsilon ?作为分母,分子的变化很小都很容易引起疏忽的变化,所以我们认为[0;0;b-2/ ? \epsilon ?] 是stiff的
- nonstiff:剩下的部分作为non-stiff的部分
Brusselator ODE test problem, fixed-point solver:
initial conditions: u0 = 1.2, v0 = 3.1, w0 = 3
problem parameters: a = 1, b = 3.5, ep = 5e-06
reltol = 1.0e-06, abstol = 1.0e-10
t u v w
----------------------------------------------
1.000000 1.103850 3.013162 3.499982
2.000000 0.688000 3.521381 3.499986
3.000000 0.409466 4.277885 3.499993
4.000000 0.367886 4.942005 3.499994
5.000000 0.413854 5.510624 3.499991
6.000000 0.589234 5.855677 3.499992
7.000000 4.756544 0.735408 3.499917
8.000000 1.813434 1.575781 3.499968
9.000000 0.527896 2.807370 3.499990
10.000000 0.305599 3.657382 3.499994
use time = 70,calc1 =[42159],calc2 = [9759]
----------------------------------------------
Final Solver Statistics:
Internal solver steps = 1621 (attempted = 1626)
Total RHS evals: Fe = 9759, Fi = 42159
Total number of fixed-point iterations = 32400
Total number of nonlinear solver convergence failures = 0
Total number of error test failures = 5
MRI方法求解
MRI方法是将系统方程拆分成快速变化的部分和缓慢变化的部分。
快速变换的部分使用小步长,缓慢变化的部分使用大步长。
MRI方法有两点需要很小心:
- 系统的拆分要拆分得好,快速变化的部分和缓慢变化的部分要符合特点,不然会引起计算失败
- 小步长和大步长要设置得好,不然也会引起计算失败
上面的两点没有很好的建议,只能通过实验测试得到。
我设置步长时,就因为没设置好,导致计算失败了。
另外,该方法效率不如DIRK方法,针对brusselator这个模型来说。