[游戏开发]第三单元 用python学习微积分（二十一）功、平均值、概率

本文内容来自于学习麻省理工学院公开课：单变量微积分-功、平均值、概率-网易公开课

一、平均值

?

由之前学过课知道，对上图中曲线函数 f(x )积分 即是求取求取在 区间中 x 轴到曲线 f(x) 之间包围的面积。

所以当曲线被分为n ( ) 个长方形时,它的面积为 约等于， 而显然 为所有分出的小矩形平均的高， 而平均的高*底边长为图形面积。所以有 ， 另一个看法是

把曲线下 a 到 b 间的图形分成n份，每份取一个f(x)值， 而每份的底边长为 , ( )所以有

(连续平均值) = AVE( f ) (f(x)在 (a,b)区间的平均值)

例1： 求f(x) = c 的定积分在a，b的平均值

当然AVE(c) = c

例2：单位半圆上（半径为1）的平均高度

from sympy import *
import numpy as np 

import matplotlib.pyplot as plt 

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.spines['left'].set_position('zero')
ax.spines['bottom'].set_position('zero')
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.set_aspect(1) 

def DrawXY(xFrom,xTo,steps,expr,color,label,plt):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    for xval in xarr:
        yval = expr.subs(x,xval)
        yarr.append(yval)
    y_nparr = np.array(yarr) 
    plt.plot(xarr, y_nparr, c=color, label=label)    

def DrawInt(xFrom,xTo,steps,expr,color,plt, label=''):
    if(xFrom < 0 and xTo < 0):
        DrawIntNegative(xFrom,xTo,steps,expr,color,plt, label)
    else:
        if(xFrom > 0 and xTo > 0):
            DrawIntPostive(xFrom,xTo,steps,expr,color,plt, label)
        else:
            DrawIntNegative(xFrom,0,steps,expr,color,plt, label)
            DrawIntPostive(0,xTo,steps,expr,color,plt, label)
    
def DrawIntNegative(xFrom1,xTo1,steps,expr,color,plt, label=''):
    xFrom = 0 - xTo1
    xTo = 0 - xFrom1
    width = (xTo - xFrom)/steps
    xarr = []
    yarr = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    xarr.append(0)
    yarr.append(0)
    for step in range(steps):
        yval = expr.subs(x,xprev)
        area += width * yval
        xarr.append(0-xprev)
        yarr.append(0-area)
        xprev= xprev + width
    plt.plot(xarr, yarr, c=color, label =label)
    
def DrawIntPostive(xFrom,xTo,steps,expr,color,plt, label=''):
    width = (xTo - xFrom)/steps
    xarr = []
    yarr = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    xarr.append(0)
    yarr.append(0)
    for step in range(steps):
        yval = expr.subs(x,xprev)
        area += width * yval
        xarr.append(xprev)
        yarr.append(area)
        xprev= xprev + width
    plt.plot(xarr, yarr, c=color, label =label)    
        
def DrawRects(xFrom,xTo,steps,expr,color,plt, label=''):
    width = (xTo - xFrom)/steps
    xarrRect = []
    yarrRect = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    for step in range(steps):
        yval = expr.subs(x,xprev + width)
        xarrRect.append(xprev)
        xarrRect.append(xprev)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev)
        yarrRect.append(0)
        yarrRect.append(yval)
        yarrRect.append(yval)
        yarrRect.append(0)
        yarrRect.append(0)
        area += width * yval
        plt.plot(xarrRect, yarrRect, c=color)    
        xprev= xprev + width
        yvalAll += yval
    print('============================')    
    if len(label)!=0:
        print(label)    
    print('============================')
    print('width = ', width)
    print('ave = ', yvalAll / steps)
    print('area = ',area)
    areaFinal = (integrate(expr, (x,xFrom,xTo)))
    print ('area final = ',areaFinal)
    print ('ave final = ', areaFinal / (xTo - xFrom))

def TangentLine(exprY,x0Val,xVal):
    diffExpr = diff(exprY)
    x1,y1,xo,yo = symbols('x1 y1 xo yo')
    expr = (y1-yo)/(x1-xo) - diffExpr.subs(x,x0Val)
    eq = expr.subs(xo,x0Val).subs(x1,xVal).subs(yo,exprY.subs(x,x0Val))
    eq1 = Eq(eq,0)
    solveY = solve(eq1)
    return xVal,solveY

def DrawTangentLine(exprY, x0Val,xVal1, xVal2, clr, txt):
    x1,y1 = TangentLine(exprY, x0Val, xVal1)
    x2,y2 = TangentLine(exprY, x0Val, xVal2)
    plt.plot([x1,x2],[y1,y2], color = clr, label=txt)
    
def Newton(expr, x0):
    ret = x0 - expr.subs(x, x0)/ expr.diff().subs(x,x0)
    return ret

   
x = symbols('x')
expr = (1 - x**2)**0.5

DrawXY(-1,1,100,expr,'blue','y = (1-x^2)^0.5',plt)

expr = -((1 - x**2)**0.5)
DrawXY(-1,1,100,expr,'green','y = -(x^2-1)^0.5',plt)

plt.legend(loc='lower right')
plt.show()

?

图1

问题是求上图中蓝色的上半圆的平均 y 是多少？

带入公式：

这里注意 是上图蓝色半圆的面积，

半径为1， S半圆

例3：求上图中蓝色半圆中弧上的点对应弧长 的平均高度

?

图2

因为这个是个单位圆， 所以我们知道半径为1， 所以半圆的长度为 , 而弧长的变化等于弧度的变化

所以 ,这时如果把角度换到x轴，则面积等于 而 的平均值为

x = symbols('x')
expr = sin(x)

DrawXY(0,np.pi,100,expr,'blue','y = sin(x)',plt)

plt.legend(loc='lower right')
plt.show()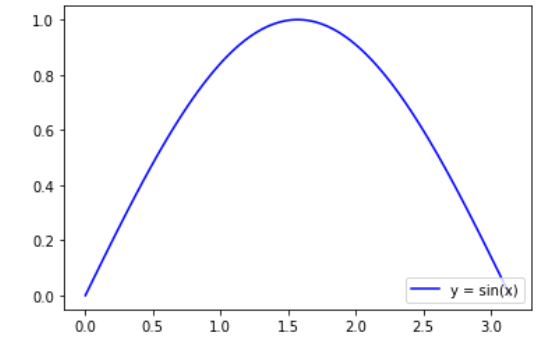

?

图3

由 图3 可知这个图形平均的y值应该是小于半圆的，也就是说在 图1 中， 从半圆的弧上随机取一个点所对应的y值(y1)，比在x轴上随机取一个点所对应的y值（y2) ， y1<y2 的概率大于

检查

print(2/np.pi>= np.pi/4)

False

二、带权重的平均值

公式：

解释一、

首先是常数的带权重平均值

这个结果符合预期，毕竟常数的权重应该是一样的，所以带权重的常数的平均值还是常数

另， 老师举了个例子， 假如一个人先后以每股10刀 / 20刀/ 30刀买入某支股票，计算买入这支股票的平均购买价格的公式为（这里的这个权重就是数量）：

三、上一讲中女巫的坩埚问题：

?

这个锅是由一个抛物线 旋转构成，顶部直径是2m, 高1m, 锅里装满水，共1600L，锅里面的水的初始温度为0摄氏度，当锅底100摄氏度时，锅的顶部温度为70摄氏度，并遵循公式 T = 100 - 30y ，问题时需要多少能量（能量=体积*温度<摄氏度>）来把锅底部加热到100摄氏度？

老师给的提示是，在锅里每一个平面（y=c）它的温度是个常数。

由于当锅的底部是100摄氏度，顶部是70摄氏度时，可以看出对于不同的高度，温度都不一样，所以只有用积分(圆盘法)来计算这个体积x温度

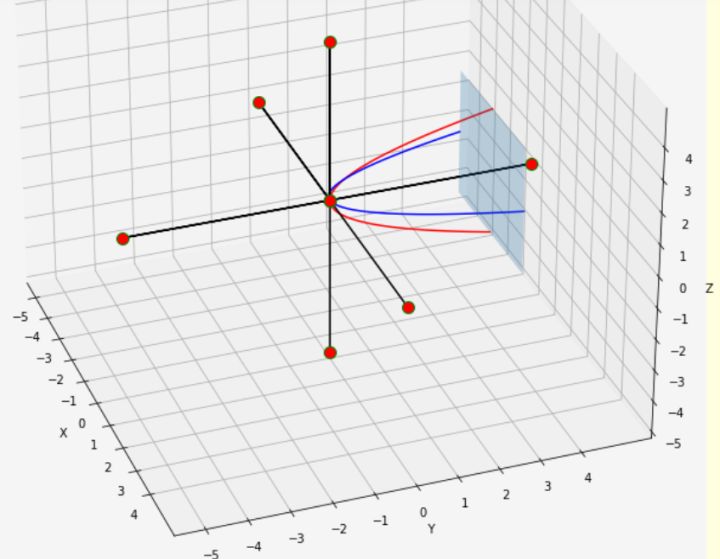
（上图代码请参考：https://zhuanlan.zhihu.com/p/479575377）

圆盘法体积：

老师的解法：

换元到x：

?

1块士力架大约250kcal ， 所以大概需要500块士力架来加热这个坩埚

注意：温度是以y=？平面为常数，所以要对y做积分

计算坩埚底部加热到100摄氏度时的平均温度，这里需要考虑到水的体积的权重,

注意锅越靠近顶部面积越大（也就是权重越大）

四、概率

x = symbols('x')
expr = 1-x**2

DrawXY(-1,1,100,expr,'blue','y = 1 - x^2',plt)
DrawRects(0.5,1,100,expr,'b',plt, label='')
plt.legend(loc='lower right')
plt.show()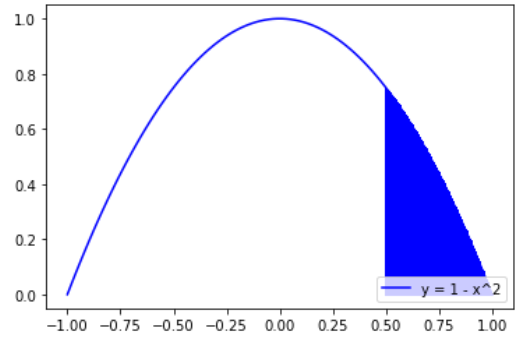

?

在区域 (上图蓝色曲线和 y=0 包围的部分) 随机取一个点 x,y), 求 P(x>0.5) ？（ｘ>0.5的概率是多少）？这个其实就是算上面蓝色实心面积和总包围面积的比 ......

概率 = 部分/总体 ( )

这里

老师的计算结果为 ,和我的不一样，python算下：

x = symbols('x')
expr = 1-x**2
print(integrate(expr, (x,0.5,1))/integrate(expr, (x,-1,1)))
print(5/32)

0.156250000000000

0.15625

我算的结果应该是对的....

求概率的一般公式：

?

下节课将介绍更多概率的问题，比如一个人打靶，靶子旁边有另一个人，那他有多大的概率会打到那个人....？