1.论文阅读

在这里插入图片描述

图2 概率扫描匹配的图形模型

??根据图2，已知x_𝑖-1 和z_𝑖-1 ，也测量到了u 和 z_𝑖 ，如何尽可能准确的求出x_𝑖 ？
??数学模型：

p(x _i|x _i-1,u,z _i-1,z _i)
??应用高斯分布，p(x _i|x _i-1,u,z _i-1,z _i) =p(z|x _i,m) p(x _i|x _i-1,u) 。其中p(x _i|x _i-1,u) 是我们熟悉的运动模型，p(z|x _i，m) 是观测模型。前者是一个常规的多元变量高斯分布问题，容易求解；在一些情况下，比如没有运动观测时，我们甚至可以略去运动模型，仅考虑观测模型即可；在另一些情况下，比如imu或轮式里程计精度不高时，我们可以调低运动模型的权重，降低其对整体概率分布的影响。但后者的计算是一个难题，因为它容易陷入局部最优解。
??这篇论文的核心贡献即在于提出了一种高效计算观测模型的方法，既能获得鲁棒的最优解，又能对解的不确定性进行量化评价，方法如下。
??我们假设Z _i中的各个激光点（以表示）位置的概率分布是彼此独立的，则：
在这里插入图片描述

对上述公式两侧同样按中的方式取对数，让乘法变加法，我们有：
------ 公式(3)

现在，公式(3) 就是我们的观测模型。那么如何来计算公式(3) ？求解过程如下（概率栅格地图）。步骤如下：
1）根据上一帧观测 z_i-1（或若干帧）建立出来的概率栅格地图！
2）按照位姿x_i把当前观测 z_i投影到 m 中，把所有被击中的栅格的概率值相加，就是！在栅格地图的基础上，公式(3) 的求解。所得的即是位姿的得分，代表着在这个位姿下，当前观测与已知环境相一致的程度（i.e., 相关性）。得分越高，表明这个位姿越靠谱。
步骤二的实现如下：
（1）获得的粗略预估；
（2）多分辨率概率查询表加速搜索全局最优位姿；
低分辨率与高分辨率栅格的定义，如图3所示：

高分辨率m，按照某个分辨率(如：0.01)把世界栅格化；
低分辨率栅格m^’,将分辨率高低（比如一倍，0.005）,构建新的栅格地图。

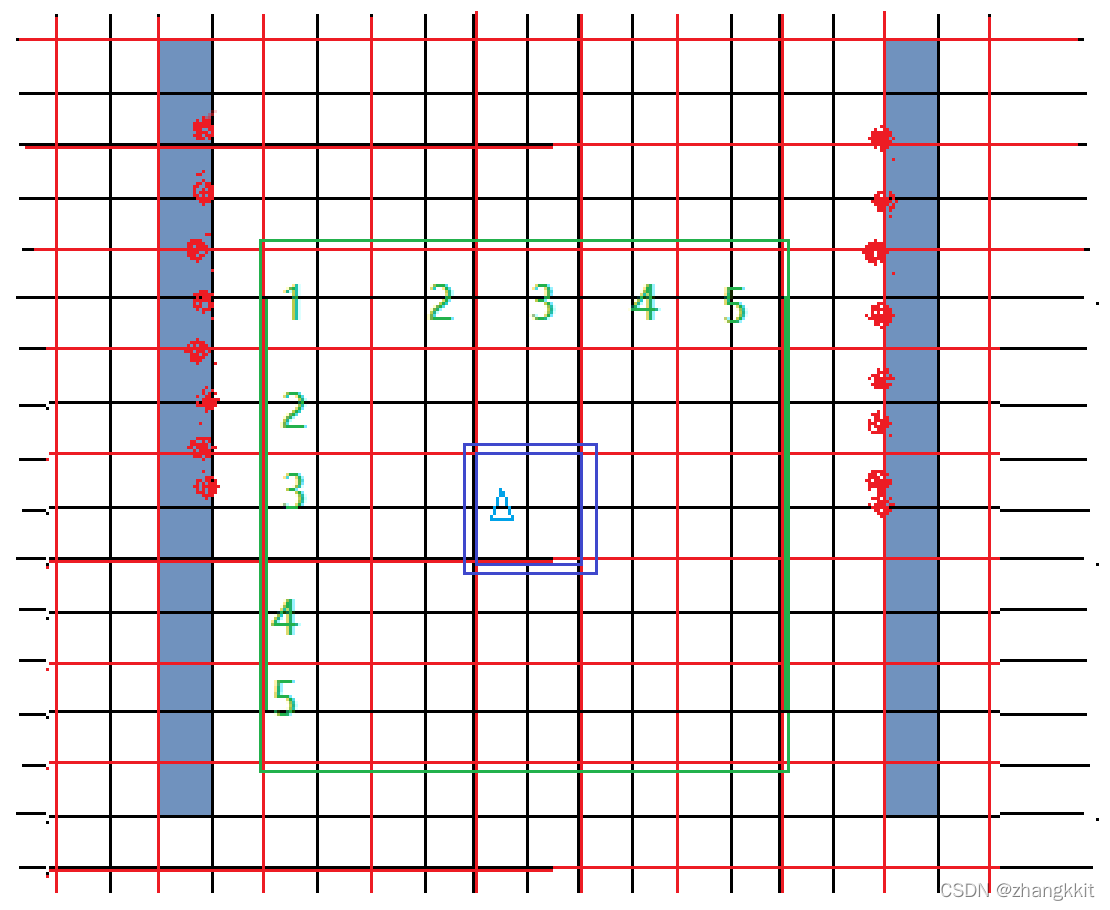
图3 高/低分辨率查询表（黑色/红色）；图中蓝色填充区域代表上一帧观测z_i，蓝色三角形代表上一个观测位置

??可以看到， m^’（红色）中的1个栅格覆盖了 m（黑色）中的4个栅格，我们把4个黑色栅格概率值的最大值赋给对应的红色栅格！——这一点非常重要。
??暴力搜索时，我们需要遍历三个变量：角度，横向平移，纵向平移。现在我们把角度放在最外层，内层就只有两个平移，这两个平移正是我们加速的对象。

??搜索空间定义：我们记 x_i 在 m中的搜索空间为 W，在m^’中同等物理尺度的搜索空间为 W^’ 。 W 与 W^’的物理空间大小是一样的，但元素的数量却不一样！举个栗子，我们设定搜索空间的物理大小为预估位姿附近〔旋转 ±10 度、横向 ±1米、纵向 ±1 米〕的空间，这里只考虑平移。假定m的分辨率是10cm，则 W中元素的个数是 100个； W^’ 的分辨率是20cm，则 W^’ 中元素的个数是25个。
在这里插入图片描述

图4 高/低分辨率查询表（黑色/红色）及关系

??加速搜索实现，设置低分辨率栅格的得分是对应所有高分辨率栅格得分的上界；
在这里插入图片描述 ??加速搜索做法：

在这里插入图片描述加速的思想很简单：低分辨率栅格的得分是对应所有高分辨率栅格得分的上界，如果某个低分辨率栅格的得分低于 H_best，则其对应的所有高分辨率栅格的得分必然也不会高于 H_best，我们索性不再考虑这部分高分辨率栅格，这个过程，也叫做「剪枝」！我们正是通过剪掉不必考虑的分支，来实现加速的。
??CSM帧匹配算法「分支定界」加速的完整示意图如下所示~
在这里插入图片描述