@创建于:2022.03.28
@修改于:2022.03.28
1、Auto-Arima介绍
ARIMA是一种非常流行的时间序列预测方法,它是自回归综合移动平均(Auto-Regressive Integrated Moving Averages)的首字母缩写。ARIMA模型建立在以下假设的基础上:
- 数据序列是平稳的,这意味着均值和方差不应随时间而变化。通过对数变换或差分可以使序列平稳。
- 输入的数据必须是单变量序列,因为ARIMA利用过去的数值预测未来的数值。
ARIMA有三个分量:AR(自回归项)、I(差分项)和MA(移动平均项):
- AR项是指用于预测下一个值的过去值。AR项由ARIMA中的参数‘p’定义。“p”的值是由PACF图确定的。
- MA项定义了预测未来值时过去预测误差的数目。ARIMA中的参数‘q’代表MA项。ACF图用于识别正确的‘q’值。
- 差分顺序规定了对序列执行差分操作的次数,对数据进行差分操作的目的是使之保持平稳。像ADF和KPSS这样的测试可以用来确定序列是否是平稳的,并有助于识别d值。
通过预测结果来推断模型阶数的好坏毕竟还是耗时耗力了些,一般可以通过计算AIC或BIC的方式来找出更好的阶数组合。pmdarima模块的auto_arima方法就可以让我们指定一个阶数上限和信息准则计算方法,从而找到信息准则最小的阶数组合。
2、安装
pip
pip install pmdarima
conda
conda config --add channels conda-forge
conda config --set channel_priority strict
conda install pmdarima
3、代码示例
Fitting a simple auto-ARIMA on the wineind dataset:
import pmdarima as pm
from pmdarima.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
# Load/split your data
y = pm.datasets.load_wineind()
train, test = train_test_split(y, train_size=150)
# Fit your model
model = pm.auto_arima(train, seasonal=True, m=12)
# 到底需不需要fit?官方没有fit
# http://www.javashuo.com/article/p-kbvzydbl-ee.html
# model.fit(train)
# 模型导出与载入
import joblib
joblib.dump(model,'auto_arima.pkl')
# model = joblib.load(model,'auto_arima.pkl')
# make your forecasts
# predict N steps into the future
forecasts = model.predict(test.shape[0])
# Visualize the forecasts (blue=train, green=forecasts)
x = np.arange(y.shape[0])
plt.plot(x[:150], train, c='blue')
plt.plot(x[150:], forecasts, c='green')
plt.show()
4、参数介绍
4.1 全参数英文介绍
调出参数方式
from pmdarima.arima import auto_arima
help(auto_arima)
Help on function auto_arima in module pmdarima.arima.auto:
auto_arima(y, X=None, start_p=2, d=None, start_q=2, max_p=5, max_d=2, max_q=5, start_P=1, D=None, start_Q=1, max_P=2, max_D=1, max_Q=2, max_order=5, m=1, seasonal=True, stationary=False, information_criterion='aic', alpha=0.05, test='kpss', seasonal_test='ocsb', stepwise=True, n_jobs=1, start_params=None, trend=None, method='lbfgs', maxiter=50, offset_test_args=None, seasonal_test_args=None, suppress_warnings=True, error_action='trace', trace=False, random=False, random_state=None, n_fits=10, return_valid_fits=False, out_of_sample_size=0, scoring='mse', scoring_args=None, with_intercept='auto', sarimax_kwargs=None, **fit_args)
Automatically discover the optimal order for an ARIMA model.
The auto-ARIMA process seeks to identify the most optimal
parameters for an ``ARIMA`` model, settling on a single fitted ARIMA model.
This process is based on the commonly-used R function,
``forecast::auto.arima`` [3].
Auto-ARIMA works by conducting differencing tests (i.e.,
Kwiatkowski–Phillips–Schmidt–Shin, Augmented Dickey-Fuller or
Phillips–Perron) to determine the order of differencing, ``d``, and then
fitting models within ranges of defined ``start_p``, ``max_p``,
``start_q``, ``max_q`` ranges. If the ``seasonal`` optional is enabled,
auto-ARIMA also seeks to identify the optimal ``P`` and ``Q`` hyper-
parameters after conducting the Canova-Hansen to determine the optimal
order of seasonal differencing, ``D``.
In order to find the best model, auto-ARIMA optimizes for a given
``information_criterion``, one of ('aic', 'aicc', 'bic', 'hqic', 'oob')
(Akaike Information Criterion, Corrected Akaike Information Criterion,
Bayesian Information Criterion, Hannan-Quinn Information Criterion, or
"out of bag"--for validation scoring--respectively) and returns the ARIMA
which minimizes the value.
Note that due to stationarity issues, auto-ARIMA might not find a
suitable model that will converge. If this is the case, a ``ValueError``
will be thrown suggesting stationarity-inducing measures be taken prior
to re-fitting or that a new range of ``order`` values be selected. Non-
stepwise (i.e., essentially a grid search) selection can be slow,
especially for seasonal data. Stepwise algorithm is outlined in Hyndman and
Khandakar (2008).
Parameters
----------
y : array-like or iterable, shape=(n_samples,)
The time-series to which to fit the ``ARIMA`` estimator. This may
either be a Pandas ``Series`` object (statsmodels can internally
use the dates in the index), or a numpy array. This should be a
one-dimensional array of floats, and should not contain any
``np.nan`` or ``np.inf`` values.
X : array-like, shape=[n_obs, n_vars], optional (default=None)
An optional 2-d array of exogenous variables. If provided, these
variables are used as additional features in the regression
operation. This should not include a constant or trend. Note that
if an ``ARIMA`` is fit on exogenous features, it must be provided
exogenous features for making predictions.
start_p : int, optional (default=2)
The starting value of ``p``, the order (or number of time lags)
of the auto-regressive ("AR") model. Must be a positive integer.
d : int, optional (default=None)
The order of first-differencing. If None (by default), the value
will automatically be selected based on the results of the ``test``
(i.e., either the Kwiatkowski–Phillips–Schmidt–Shin, Augmented
Dickey-Fuller or the Phillips–Perron test will be conducted to find
the most probable value). Must be a positive integer or None. Note
that if ``d`` is None, the runtime could be significantly longer.
start_q : int, optional (default=2)
The starting value of ``q``, the order of the moving-average
("MA") model. Must be a positive integer.
max_p : int, optional (default=5)
The maximum value of ``p``, inclusive. Must be a positive integer
greater than or equal to ``start_p``.
max_d : int, optional (default=2)
The maximum value of ``d``, or the maximum number of non-seasonal
differences. Must be a positive integer greater than or equal to ``d``.
max_q : int, optional (default=5)
The maximum value of ``q``, inclusive. Must be a positive integer
greater than ``start_q``.
start_P : int, optional (default=1)
The starting value of ``P``, the order of the auto-regressive portion
of the seasonal model.
D : int, optional (default=None)
The order of the seasonal differencing. If None (by default, the value
will automatically be selected based on the results of the
``seasonal_test``. Must be a positive integer or None.
start_Q : int, optional (default=1)
The starting value of ``Q``, the order of the moving-average portion
of the seasonal model.
max_P : int, optional (default=2)
The maximum value of ``P``, inclusive. Must be a positive integer
greater than ``start_P``.
max_D : int, optional (default=1)
The maximum value of ``D``. Must be a positive integer greater
than ``D``.
max_Q : int, optional (default=2)
The maximum value of ``Q``, inclusive. Must be a positive integer
greater than ``start_Q``.
max_order : int, optional (default=5)
Maximum value of p+q+P+Q if model selection is not stepwise.
If the sum of ``p`` and ``q`` is >= ``max_order``, a model will
*not* be fit with those parameters, but will progress to the next
combination. Default is 5. If ``max_order`` is None, it means there
are no constraints on maximum order.
m : int, optional (default=1)
The period for seasonal differencing, ``m`` refers to the number of
periods in each season. For example, ``m`` is 4 for quarterly data, 12
for monthly data, or 1 for annual (non-seasonal) data. Default is 1.
Note that if ``m`` == 1 (i.e., is non-seasonal), ``seasonal`` will be
set to False. For more information on setting this parameter, see
:ref:`period`.
seasonal : bool, optional (default=True)
Whether to fit a seasonal ARIMA. Default is True. Note that if
``seasonal`` is True and ``m`` == 1, ``seasonal`` will be set to False.
stationary : bool, optional (default=False)
Whether the time-series is stationary and ``d`` should be set to zero.
information_criterion : str, optional (default='aic')
The information criterion used to select the best ARIMA model. One of
``pmdarima.arima.auto_arima.VALID_CRITERIA``, ('aic', 'bic', 'hqic',
'oob').
alpha : float, optional (default=0.05)
Level of the test for testing significance.
test : str, optional (default='kpss')
Type of unit root test to use in order to detect stationarity if
``stationary`` is False and ``d`` is None. Default is 'kpss'
(Kwiatkowski–Phillips–Schmidt–Shin).
seasonal_test : str, optional (default='ocsb')
This determines which seasonal unit root test is used if ``seasonal``
is True and ``D`` is None. Default is 'OCSB'.
stepwise : bool, optional (default=True)
Whether to use the stepwise algorithm outlined in Hyndman and Khandakar
(2008) to identify the optimal model parameters. The stepwise algorithm
can be significantly faster than fitting all (or a ``random`` subset
of) hyper-parameter combinations and is less likely to over-fit
the model.
n_jobs : int, optional (default=1)
The number of models to fit in parallel in the case of a grid search
(``stepwise=False``). Default is 1, but -1 can be used to designate
"as many as possible".
start_params : array-like, optional (default=None)
Starting parameters for ``ARMA(p,q)``. If None, the default is given
by ``ARMA._fit_start_params``.
method : str, optional (default='lbfgs')
The ``method`` determines which solver from ``scipy.optimize``
is used, and it can be chosen from among the following strings:
- 'newton' for Newton-Raphson
- 'nm' for Nelder-Mead
- 'bfgs' for Broyden-Fletcher-Goldfarb-Shanno (BFGS)
- 'lbfgs' for limited-memory BFGS with optional box constraints
- 'powell' for modified Powell's method
- 'cg' for conjugate gradient
- 'ncg' for Newton-conjugate gradient
- 'basinhopping' for global basin-hopping solver
The explicit arguments in ``fit`` are passed to the solver,
with the exception of the basin-hopping solver. Each
solver has several optional arguments that are not the same across
solvers. These can be passed as **fit_kwargs
trend : str or None, optional (default=None)
The trend parameter. If ``with_intercept`` is True, ``trend`` will be
used. If ``with_intercept`` is False, the trend will be set to a no-
intercept value.
maxiter : int, optional (default=50)
The maximum number of function evaluations. Default is 50.
offset_test_args : dict, optional (default=None)
The args to pass to the constructor of the offset (``d``) test. See
``pmdarima.arima.stationarity`` for more details.
seasonal_test_args : dict, optional (default=None)
The args to pass to the constructor of the seasonal offset (``D``)
test. See ``pmdarima.arima.seasonality`` for more details.
suppress_warnings : bool, optional (default=True)
Many warnings might be thrown inside of statsmodels. If
``suppress_warnings`` is True, all of the warnings coming from
``ARIMA`` will be squelched. Note that this will not suppress
UserWarnings created by bad argument combinations.
error_action : str, optional (default='warn')
If unable to fit an ``ARIMA`` for whatever reason, this controls the
error-handling behavior. Model fits can fail for linear algebra errors,
convergence errors, or any number of problems related to stationarity
or input data.
- 'warn': Warns when an error is encountered (default)
- 'raise': Raises when an error is encountered
- 'ignore': Ignores errors (not recommended)
- 'trace': Logs the entire error stacktrace and continues the
search. This is the best option when trying to determine why a
model is failing.
trace : bool or int, optional (default=False)
Whether to print status on the fits. A value of False will print no
debugging information. A value of True will print some. Integer values
exceeding 1 will print increasing amounts of debug information at each
fit.
random : bool, optional (default=False)
Similar to grid searches, ``auto_arima`` provides the capability to
perform a "random search" over a hyper-parameter space. If ``random``
is True, rather than perform an exhaustive search or ``stepwise``
search, only ``n_fits`` ARIMA models will be fit (``stepwise`` must be
False for this option to do anything).
random_state : int, long or numpy ``RandomState``, optional (default=None)
The PRNG for when ``random=True``. Ensures replicable testing and
results.
n_fits : int, optional (default=10)
If ``random`` is True and a "random search" is going to be performed,
``n_iter`` is the number of ARIMA models to be fit.
return_valid_fits : bool, optional (default=False)
If True, will return all valid ARIMA fits in a list. If False (by
default), will only return the best fit.
out_of_sample_size : int, optional (default=0)
The ``ARIMA`` class can fit only a portion of the data if specified,
in order to retain an "out of bag" sample score. This is the
number of examples from the tail of the time series to hold out
and use as validation examples. The model will not be fit on these
samples, but the observations will be added into the model's ``endog``
and ``exog`` arrays so that future forecast values originate from the
end of the endogenous vector.
For instance::
y = [0, 1, 2, 3, 4, 5, 6]
out_of_sample_size = 2
> Fit on: [0, 1, 2, 3, 4]
> Score on: [5, 6]
> Append [5, 6] to end of self.arima_res_.data.endog values
scoring : str, optional (default='mse')
If performing validation (i.e., if ``out_of_sample_size`` > 0), the
metric to use for scoring the out-of-sample data. One of ('mse', 'mae')
scoring_args : dict, optional (default=None)
A dictionary of key-word arguments to be passed to the ``scoring``
metric.
with_intercept : bool or str, optional (default="auto")
Whether to include an intercept term. Default is "auto" which behaves
like True until a point in the search where the sum of differencing
terms will explicitly set it to True or False.
sarimax_kwargs : dict or None, optional (default=None)
Keyword arguments to pass to the ARIMA constructor.
**fit_args : dict, optional (default=None)
A dictionary of keyword arguments to pass to the :func:`ARIMA.fit`
method.
See Also
--------
:func:`pmdarima.arima.ARIMA`
Notes
-----
* Fitting with `stepwise=False` can prove slower, especially when
`seasonal=True`.
References
----------
.. [1] https://wikipedia.org/wiki/Autoregressive_integrated_moving_average
.. [2] R's auto-arima source code: https://github.com/robjhyndman/forecast/blob/master/R/arima.R
.. [3] R's auto-arima documentation: https://www.rdocumentation.org/packages/forecast
4.2 部分参数中文解释
1.start_p:p的起始值,自回归(“AR”)模型的阶数(或滞后时间的数量),必须是正整数
2.start_q:q的初始值,移动平均(MA)模型的阶数。必须是正整数。
3.max_p:p的最大值,必须是大于或等于start_p的正整数。
4.max_q:q的最大值,必须是一个大于start_q的正整数
5.seasonal:是否适合季节性ARIMA。默认是正确的。注意,如果season为真,而m == 1,则season将设置为False。
6.stationary :时间序列是否平稳,d是否为零。
6.information_criterion:信息准则用于选择最佳的ARIMA模型。(‘aic’,‘bic’,‘hqic’,‘oob’)之一
7.alpha:检验水平的检验显著性,默认0.05
8.test:如果stationary为假且d为None,用来检测平稳性的单位根检验的类型。默认为‘kpss’;可设置为adf
9.n_jobs :网格搜索中并行拟合的模型数(逐步=False)。默认值是1,但是-1可以用来表示“尽可能多”。
10.suppress_warnings:statsmodel中可能会抛出许多警告。如果suppress_warnings为真,那么来自ARIMA的所有警告都将被压制
11.error_action:如果由于某种原因无法匹配ARIMA,则可以控制错误处理行为。(warn,raise,ignore,trace)
12.max_d:d的最大值,即非季节差异的最大数量。必须是大于或等于d的正整数。
13.trace:是否打印适合的状态。如果值为False,则不会打印任何调试信息。值为真会打印一些
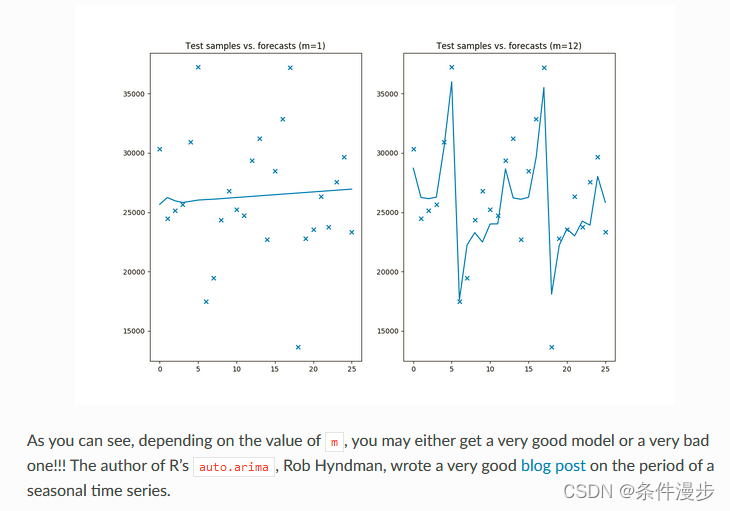
4.3 参数m