[游戏开发]python计算机视觉-局部图像描述子

局部图像描述子

Harris角点

角点（corner points）

• 局部窗口沿各方向移动，均产生明显的变化的点
• 图像局部曲率突变的点

不同类型的角点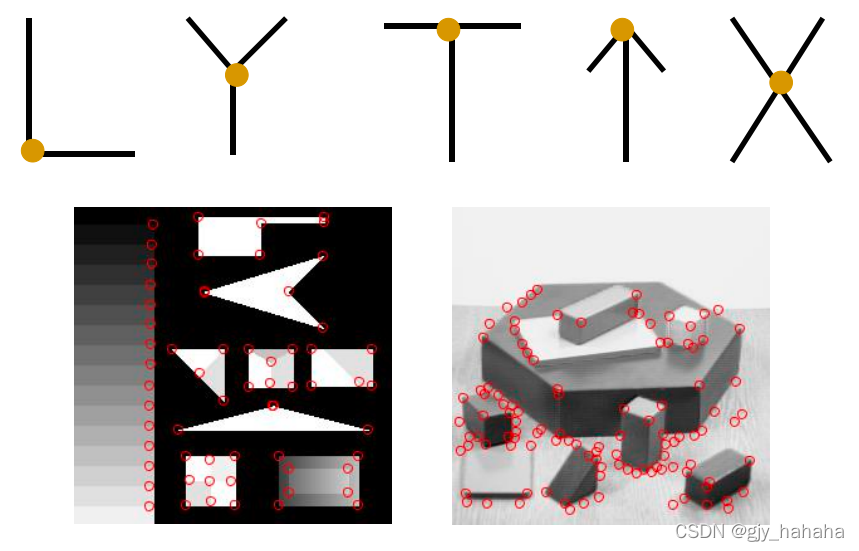

角点检测算法

好的角点检测算法需具备以下特点：

• 能够检测出图像中“真实的”角点
• 拥有准确的定位性能
• 具有很高的稳定性
• 具有对噪声的鲁棒性
• 具有较高的计算效率

典型的角点检测算法有：

• Harris角点检测
• CSS角点检测

HARRIS角点检测算法的基本思想

• 从图像局部的小窗口观察图像特征
• 角点定义：窗口向任意方向移动都导致图像灰度的明显变化
  

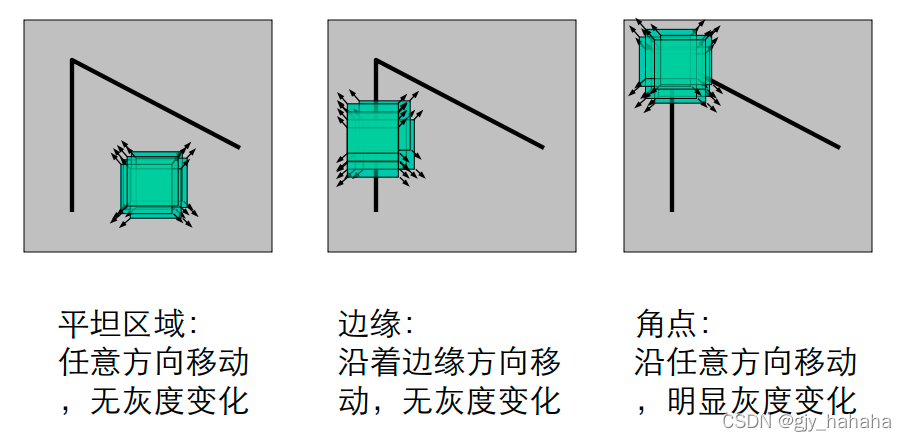
Harris检测当中的数学表达

在上面的角点定义当中，我们知道判断角点需要判断窗口向任意方向移动时是否导致了图像灰度的变化，因此，我们可以将图像窗口平移[u,v]产生灰度变化E(u,v)用如下数学表达式表示：

该表达式当中，$I(x,y)$表示图像灰度，$I(x+u,y+v)$表示平移后的图像灰度，$w(x,y)$表示窗口函数

那么如何对$I(x+u,y+v)$以及$E(u,v)$进行求解？
首先我们将$I(x+u,y+v)$在$(x,y)$处进行泰勒展开，可以得到下式：
$I(x+u,y+v)=I(x,y)+I_{x}u+I_{y}v+O(u^2,v^2)$
然后将上式再代回原式中，便可得到：
$E(u,v)={\sum }_{x,y}w(x,y)[I_{x}u+I_{y}v+O(u^2,v^2){]}^2\approx {\sum }_{x,y}w(x,y)[I_{x}u+I_{y}v{]}^2$

对于局部微小的移动量$[u,v]$,便可得到以下表达式：

在该式中，M为2*2的矩阵，可由图像导数求得：

记M的特征值为${\lambda }_1$,${\lambda }_2$,我们可以通过M的两个特征值的大小对图像点进行分类：


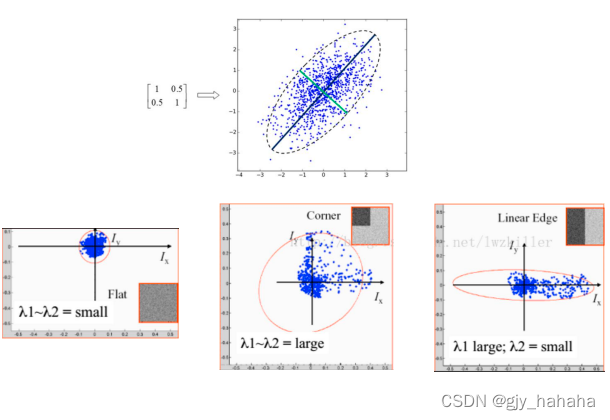
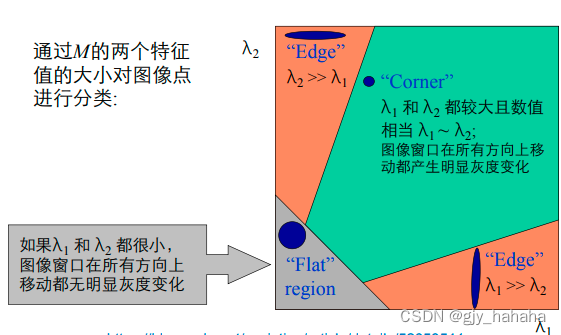
角点响应函数R：
$R=detM?k(traceM{)}^2$
$detM={\lambda }_1{\lambda }_2$
$traceM={\lambda }_1+{\lambda }_2$
(k-empirical constant,k=0.04~0.06)

• R只与M的特征值有关
• 角点：R为大数值正数
• 边缘：R为大数值负数
• 平坦区：R为小数值
  

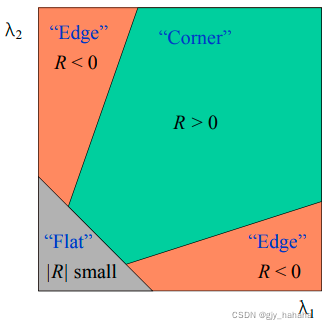
Harris角点检测器响应函数

def compute_harris_response(im,sigma=3):
    # 在一幅灰度图像中，对每个像素计算Harris角点检测器响应函数
    # 计算导数
    imx=zeros(im.shape)
    filters.gaussian_filter(im,(sigma,sigma),(0,1),imx)
    imy=zeros(im.shape)
    filters.gaussian_filter(im,(sigma,sigma),(1,0),imy)
    #计算Harris矩阵的分量
    Wxx=filters.gaussian_filter(imx*imx,sigma)
    Wxy=filters.gaussian_filter(imx*imy,sigma)
    Wyy=filters.gaussian_filter(imy*imy,sigma)
    #计算特征值和迹
    Wdet=Wxx*Wyy-Wxy**2
    Wtr=Wxx+Wyy
    return Wdet/Wtr

该函数会返回像素值为Harris响应函数值的一幅图像。我们需要从图像中挑选出需要的信息，然后选取像素值高于阈值的所有图像点，再加上额外的限制，即角点之间间隔必须大于设定的最小距离，这样会产生很好的角点检测结果。为了实现该算法，我们获取所有候选像素点，以角点响应值递减的顺序排序，然后将距离已标记为角点位置过近的区域从候选像素点中删除。具体函数如下所示：

def get_harris_points(harrisim,min_dist=10,threshold=0.1):
    #从一幅Harris响应图像中返回角点，min_dist为分隔角点和图像边界的最少像素数目
    #寻找高于阈值的候选角点
    corner_threshold=harrisim.max()*threshold
    harrisim_t=(harrisim>corner_threshold)*1
    #得到候选点的坐标
    coords=array(harrisim_t.nonzero()).T
    # 以及它们的Harris响应值
    candidate_values=[harrisim[c[0],c[1]]for c in coords]
    #对候选点按照Harris响应值进行排序
    index=argsort(candidate_values)
    #将可行点的位置保存到数组中
    allowed_locations=zeros(harrisim.shape)
    allowed_locations[min_dist:-min_dist,min_dist:-min_dist]=1
    #按照min_distance原则，选择最佳Harris点
    filtered_coords=[]
    for i in index:
        if allowed_locations[coords[i,0],coords[i,1]]==1:
            filtered_coords.append(coords[i])
            allowed_locations[(coords[i,0]-min_dist):(coords[i,0]+min_dist),(coords[i,1]-min_dist):(coords[i,1]+min_dist)]=0
    return filtered_coords

绘制角点函数：

def plot_harris_points(image,filtered_coords):
    # 绘制图像中检测到的角点
    figure()
    gray()
    imshow(image)
    plot([p[1]for p in filtered_coords],[p[0]for p in filtered_coords],'*')
    axis('off')
    show()

绘制角点后的效果图：

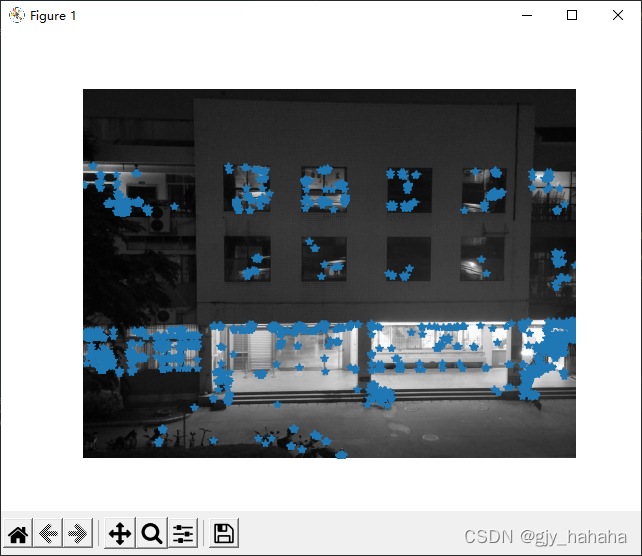
Harris角点检测

# 读入图像
im = array(Image.open('./1.jpg').convert('L'))

# 检测harris角点
harrisim = harris.compute_harris_response(im)

# Harris响应函数
harrisim1 = 255 - harrisim

figure()
gray()

#画出Harris响应图
subplot(141)
imshow(harrisim1)
print (harrisim1.shape)
axis('off')
axis('equal')

threshold = [0.01, 0.05, 0.1]
for i, thres in enumerate(threshold):
    filtered_coords = harris.get_harris_points(harrisim, 6, thres)
    subplot(1, 4, i+2)
    s = str(thres)
    title(r'σ=' + s)
    imshow(im)
    print (im.shape)
    plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
    axis('off')

#原书采用的PCV中PCV harris模块
#harris.plot_harris_points(im, filtered_coords)

# plot only 200 strongest
# harris.plot_harris_points(im, filtered_coords[:200])

show()

运行结果：

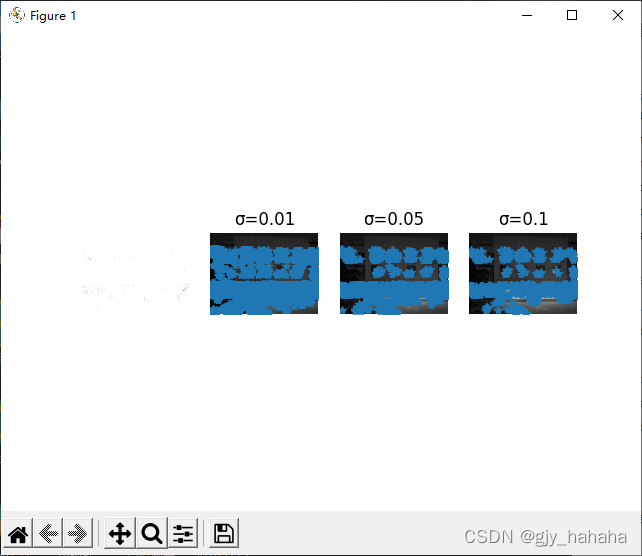
由图所示：当σ值分别为0.01，0.05，0.1时检测出的角点数量并不相同，提高阈值σ，则寻找到的高于阈值的候选角点越少，检测出的角点数量减少。

Harris角点检测的优缺点

• Harris角点检测算子具有旋转不变性
  Harris角点检测算子使用角点附近的区域灰度二阶矩阵，二阶矩阵可以表示为椭圆，椭圆长短轴为二阶矩阵特征值平方根的倒数，当特征椭圆转动时，特征值不发生变化，判断角点响应值也不发生变化，因此Harris角点检测算子具有旋转不变性
• Harris角点检测算子对于灰度平移和灰度尺度变化不敏感
  在进行Harris角点检测时，使用了微分运算，微分运算对于图像亮度变化不敏感，即对亮度和对比度的仿射变换不影响Harris响应极值点出现位置，但阈值的选择会影响角点检测的数量
• Harris角点检测算子不具备尺度不变性
  当将一幅图像进行放大或缩小后，在检测窗口尺度不变的前提下，原图与放缩后的图像在窗口中包含的内容是不一样的，因此对于角点的检测就会发生偏差

在图像间寻找对应点

Harris角点检测器仅能检测出图像中的兴趣点，但没有给出通过比较图像间的兴趣点来寻找匹配角点的方法，我们需要在每个点上加入描述子信息，并给出一个比较这些描述子的方法，兴趣点描述子是分配给兴趣点的一个向量，描述该点附近的图像的表观信息，描述子越好，寻找到的对应点越好，我们用对应点或者点的对应来描述相同物体和场景点在不同图像上形成的像素点。Harris角点的描述子通常是由周围图像像素块的灰度值，以及用于比较的归一化互相关矩阵构成的，图像的像素块由以该像素点为中心的周围矩形部分图像构成。

def get_descriptors(image,filtered_coords,wid=5):
    #对于每个返回的点，返回点周围2*wid+1个像素的值（假设选取点的min_distance>wid）
    desc=[]
    for coords in filtered_coords:
        patch=image[coords[0]-wid:coords[0]+wid+1,coords[1]-wid:coords[1]+wid+1].flatten()
    desc.append(patch)
    return desc
def match(desc1,desc2,threshold=0.5):
    #对于第一幅图像中的每个角点描述子，使用归一化互相关，选取它在第二幅图像中的匹配角点
    n=len[desc1[0]]
    #点对的距离
    d=-ones((len(desc1),len(desc2)))
    for i in range(len(desc1)):
        for j in range(len(desc2)):
            d1=(desc1[i]-mean(desc1[i]))/std(desc1[i])
            d2=(desc2[i]-mean(desc2[i]))/std(desc2[i])
            ncc_value=sum(d1*d2)/(n-1)
            if ncc_value>threshold:
                d[i,j]=ncc_value
    ndx=argsort(-d)
    matchscores=ndx[:,0]
    return matchscores
def match_twosided(desc1,desc2,threshold=0.5):
    #两边对称版本的match（）
    matches_12=match(desc1, desc2, threshold)
    matches_21 = match(desc2, desc1, threshold)
    ndx_12=where(matches_12>=0)[0]
    #去除非对称的匹配
    for n in ndx_12:
        if matches_21[matches_12[n]]!=n:
            matches_12[n]=-1
    return matches_12
def appendimages(im1,im2):
    #返回将两幅图像并排拼接成的一幅新图像
    #选取具有最少行数的图像，然后填充足够的空行
    rows1=im1.shape[0]
    rows2 = im2.shape[0]
    if rows1<rows2:
        im1=concatenate((im1,zeros((rows2-rows1,im1.shape[1]))),axis=0)
    elif rows1>rows2:
        im2 = concatenate((im2, zeros((rows1 - rows2, im2.shape[1]))), axis=0)
    #如果这些情况都没有，那么它们的行数相同，不需要进行填充
    return concatenate((im1,im2),axis=1)
def plot_matches(im1,im2,locs1,locs2,matchscores,show_below=True):
    #显示一幅带有连接匹配之间连线的图片，输入：im1,im2（数组图像），locs1,locs2(特征位置），matchscores(match()的输出),show_below（如果图像应该显示在匹配的下方）
    im3=appendimages(im1,im2)
    if show_below:
        im3=vstack((im3,im3))
    imshow(im3)
    cols1=im1.shape[1]
    for i,m in enumerate(matchscores):
        if m>0:
            plot([locs1[i][1],locs2[m][1]+cols1],[locs1[i][0],locs2[m][0]],'c')
    axis('off')

from pylab import *
from PIL import Image

from PCV.localdescriptors import harris
from PCV.tools.imtools import imresize

# Figure 2-2上面的图
#im1 = array(Image.open("../data/crans_1_small.jpg").convert("L"))
#im2= array(Image.open("../data/crans_2_small.jpg").convert("L"))

# Figure 2-2下面的图
im1 = array(Image.open("./1.jpg").convert("L"))
im2 = array(Image.open("./3.jpg").convert("L"))

# resize加快匹配速度
im1 = imresize(im1, (im1.shape[1]//2, im1.shape[0]//2))
im2 = imresize(im2, (im2.shape[1]//2, im2.shape[0]//2))

if __name__=='__main__':
    wid = 5
    harrisim = harris.compute_harris_response(im1, 5)
    filtered_coords1 = harris.get_harris_points(harrisim, wid+1)
    d1 = harris.get_descriptors(im1, filtered_coords1, wid)

    harrisim = harris.compute_harris_response(im2, 5)
    filtered_coords2 = harris.get_harris_points(harrisim, wid+1)
    d2 = harris.get_descriptors(im2, filtered_coords2, wid)

    print ('starting matching')
    matches = harris.match_twosided(d1, d2)

    figure()
    gray()
    harris.plot_matches(im1, im2, filtered_coords1, filtered_coords2, matches)
    show()

运行结果：

由图所示：在图像当中寻找对应点时，虽能找到一些对应点，但同样存在着不正确的匹配点，因为图像像素块的互相关矩阵具有较弱的描述性，并且这些描述符不具有尺度不变性和旋转不变性，算法中像素块大小也会影响到对应匹配的结果。

SIFT（尺度不变特征变换）

SIFT特征包括兴趣点检测器和描述子，SIFT描述子具有非常强的稳健性，这很大程度上也是SIFT特征能够成功和流行的主要原因，SIFT特征对于尺度、旋转和亮度都具有不变性，因此，它可以用于三维视角和噪声的可靠匹配。

SIFT算法可以解决的问题

• 目标的旋转、缩放、平移（RST）
• 图像仿射/投影变换（视点viewpoint）
• 弱光照影响（illumination）
• 部分目标遮挡（occlusion）
• 杂物场景（clutter）
• 噪声

SIFT算法实现细节

SIFT算法的实现实质上是在不同尺度空间上查找特征点（关键点）。

SIFT算法实现特征匹配流程：

• 提取关键点
• 对关键点附加详细的信息（局部特征），即描述符
• 通过特征点（附带上特征向量的关键点）的两两比较找出相互匹配的若干对特征点，建立景物间的对应关系

关键点检测

什么是关键点（特征点）

SIFT要查找的关键点是一些十分突出的点，不会因光照、尺度、旋转等因素的改变而消失，比如角点、边缘点、暗区域的亮点以及亮区域的暗点。据归纳，我们可以看出SIFT特征点希望选出具有下述不变性的点：

• 尺度
• 方向
• 位移
• 光照

什么是尺度空间

尺度空间的主要思想是通过对原图像进行尺度变换，获得多尺度下的空间表示，从而实现边缘、角点检测和不同分辨率上的特征提取，以满足特征点的尺度不变性。
尺度越大图像越模糊

高斯金字塔

高斯金字塔的构建过程：

1. 对图像做高斯平滑
2. 对图像做降采样
   为了让尺度体现连续性，在简单下采样的基础上加上高斯滤波，一幅图像可以产生几组图像，一组图像包括基层图像

DoG

DoG（Difference of Gaussian）函数

Dog在计算上只要相邻高斯平滑后图像相减，因此简化了计算

DoG高斯差分金字塔

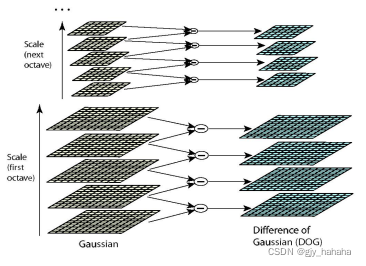
可以通过高斯差分图像看出图像上的像素值变化情况（若没有变化，即没有特征，特征需是变化尽可能多的点）DoG图像描绘的是目标的轮廓。

DoG局部极值检测

• DoG的局部极值点
  特征点是由DoG空间的局部极值点组成的，为了寻找DoG函数的极值点，每个像素点都要和它的所有相邻点比较，看其是否比它的图像域和尺度域的相邻点大或小
• 去除边缘响应
  DoG函数在图像边缘有较强的边缘响应，因此需要排除边缘响应

关键点方向分配

通过尺度不变性求极值点可以使其具有缩放不变的性质，利用关键点领域像素的梯度方向分布特性，可以为每个关键点指定方向参数方向，从而使描述子对图像旋转具有不变性。通过求每个极值点的梯度为极值点赋予方向。
像素点的梯度表示：
$gradI(x,y)=(\frac{\delta I}{\delta x},\frac{\delta I}{\delta y})$
梯度幅值：
$m(x,y)=\sqrt{(L(x+1,y)?L(x?1,y){)}^2+(L(x,y+1)?L(x,y?1){)}^2}$
梯度方向：
$\theta (x,y)=ta{n}^{?1}[\frac{L(x,y+1)?L(x,y?1)}{L(x+1,y)?L(x?1,y)}]$
方向直方图的生成

确定关键点的方向采用梯度直方图统计法，统计以关键点为原点，一定区域内的图像像素点对关键点方向生成所作的贡献
关键点主方向：极值点周围区域梯度直方图的主峰值也是特征点方向
关键点辅方向：在梯度方向直方图中，当存在另一个相当于主峰值80%能量的峰值时，则将这个方向认为是该关键点的辅方向
这可以增强匹配的鲁棒性

如图所示：

描述子由2×2×8维向量表征，即是2×2个8方向的方向直方图组成。左边的种子点由8×8单元组成，每个小格代表特征点邻域所在尺度空间的一个像素，箭头方向代表像素梯度方向，箭头长度代表该像素的幅值，然后在4×4的窗口内计算8个方向的梯度方向直方图，绘制每个梯度方向的累加可形成一个种子点，如右边所示，一个特征点由4个种子点的信息组成
Lowe实验结果表明：描述子采用4×4×8=128维向量表征，综合效果最优（不变性与独特性）

关键点匹配

分别对模板图（参考图）和实时图（观测图）建立关键点描述子集合，目标的识别是通过两点集内关键点描述子的比对来完成，具有128维的关键点描述子的相似性度量采用欧式距离。
关键点的匹配可采用穷举法，但耗费时间太多，一般采用kd树的数据结构来完成搜索，搜索内容是以目标图像的关键点为基准，搜索与目标图像的特征点最邻近的原图像特征点和次邻近的原图像特征点。

检测兴趣点

首先将图像转换成.pgm格式文件，转换结果以易读格式保存在文本文件中。

def process_image(imagename,resultname,params="--edge-thresh 10 --peak-thresh 5"):
    #处理一幅图像，然后将结果保存在文件中
    if imagename[-3:]!='pgm':
        #创建一个pgm文件
        im=Image.open(imagename).convert('L')
        im.save('tmp.pgm')
        imagename='tmp.pgm'
    cmmd=str("sift "+imagename+"--output="+resultname+" "+params)
    os.system(cmmd)
    print('processed',imagename,'to',resultname)

读取图像特征并通过在图像上绘制出它们的位置，可以将其可视化。

def read_features_from_file(filename):
    #读取特征属性值，然后将其以矩阵的形式返回
    f=loadtxt(filename)
    return f[:,:4],f[:,4:]#特征位置，描述子
def write_features_to_file(filename,locs,desc):
    #将特征位置和描述子保存到文件中
    savetxt(filename,hstack((locs,desc)))
def plot_features(im,locs,circle=False):
    #显示带有特征的图像 输入：im（数组图像），locs（每个特征的行、列、尺度和方向角度）
    def draw_circle(c,r):
        t=arange(0,1.01,.01)*2*pi
        x=r*cos(t)+c[0]
        y=r*sin(t)+c[1]
        plot(x,y,'b',linewidth=2)
    imshow(im)
    if circle:
        for p in locs:
            draw_circle(p[:2],p[2])
    else:
        plot(locs[:,0],locs[:,1],'ob')
    axis('off')

from PIL import Image
from pylab import *
from PCV.localdescriptors import sift
from PCV.localdescriptors import harris

imname = './1.jpg'
im = array(Image.open(imname).convert('L'))
sift.process_image(imname, 'empire.sift')
l1, d1 = sift.read_features_from_file('empire.sift')

figure()
gray()
subplot(131)
sift.plot_features(im, l1, circle=False)
title(u'SIFT特征',fontproperties=font)
subplot(132)
sift.plot_features(im, l1, circle=True)
title(u'用圆圈表示SIFT特征尺度',fontproperties=font)

# 检测harris角点
harrisim = harris.compute_harris_response(im)

subplot(133)
filtered_coords = harris.get_harris_points(harrisim, 6, 0.1)
imshow(im)
plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
axis('off')
title(u'Harris角点',fontproperties=font)

show()

运行结果：

由图所示：SIFT特征和Harris角点所选择的特征点的位置不同。

描述子匹配

def match(desc1,desc2):
    #对于第一幅图像中的每个描述子，选取其在第二幅图像中的匹配 输入：desc1（第一幅图像中的描述子），desc2（第二幅图像中的描述子）
    desc1=array([d/linalg.norm(d) for d in desc1])
    desc2 = array([d / linalg.norm(d) for d in desc2])
    dist_ratio=0.6
    desc1_size=desc1.shape
    matchscores=zeros((desc1_size[0],1),'int')
    desc2t=desc2.T#预先计算矩阵转置
    for i in range(desc1_size[0]):
        dotprods=dot(desc1[i,:],desc2t)#向量点乘
        dotprods=0.9999*dotprods
        #反余弦和反排序，返回第二幅图像中特征的索引
        indx=argsort(arccos(dotprods))
        #检查最近邻的角度是否小于dist_ratio乘以第二近邻的角度
        if arccos(dotprods)[indx[0]]<dist_ratio*arccos(dotprods)[indx[1]]:
            matchscores[i]=int(indx[0])
    return matchscores

match函数使用描述子向量间的夹角作为距离度量，在此之前，我们需要将描述子向量归一化到单位长度，因为这种匹配是单向的，即我们将每个特征向另一幅图像中的所有特征进行匹配，所以我们可以先计算第二幅图像兴趣点描述子向量的转置矩阵，这样就不需要对每个特征分别进行转置操作。
为了进一步增加匹配的稳健性，我们可以反过来再执行一次该步骤，用另外方法匹配（从第二幅图像中的特征向第一幅图像中的特征匹配），最后仅保留同时满足这两种匹配准则的对应，match_twosided函数即可实现该操作：

def match_twosided(desc1,desc2):
    #双向对称版本的match（）
    matches_12=match(desc1,desc2)
    matches_21 = match(desc2, desc1)
    ndx_12=matches_12.nonzero()[0]
    #去除不对称的匹配
    for n in ndx_12:
        if matches_21[int(matches_12[n])]!=n:
            matches_12[n]=0
    return matches_12

from PIL import Image
from pylab import *
import sys
from PCV.localdescriptors import sift


if len(sys.argv) >= 3:
  im1f, im2f = sys.argv[1], sys.argv[2]
else:
  im1f = './1.jpg'
  im2f = './3.jpg'
im1 = array(Image.open(im1f))
im2 = array(Image.open(im2f))

sift.process_image(im1f, 'out_sift_1.txt')
l1, d1 = sift.read_features_from_file('out_sift_1.txt')
figure()
gray()
subplot(121)
sift.plot_features(im1, l1, circle=False)

sift.process_image(im2f, 'out_sift_2.txt')
l2, d2 = sift.read_features_from_file('out_sift_2.txt')
subplot(122)
sift.plot_features(im2, l2, circle=False)

#matches = sift.match(d1, d2)
matches = sift.match_twosided(d1, d2)
print ('{} matches'.format(len(matches.nonzero()[0])))

figure()
gray()
sift.plot_matches(im1, im2, l1, l2, matches, show_below=True)
show()

运行结果：
match函数


match_twosided函数


通过对比match函数与match_twosided函数的运行结果可以发现match_twosided函数的匹配精度较高，保留了同时满足两种匹配准则的对应，具有较好的匹配稳健性。


不同尺度下仍具有精准的匹配度


不同角度，在部分遮挡下仍能进行准确匹配

根据以上运行结果可以看出：相比较Harris角点检测，SIFT特征匹配的匹配效率较高，匹配更加精准，具有更强的匹配稳健性。

地理标记图像匹配

from pylab import *
from PIL import Image
from PCV.localdescriptors import sift
from PCV.tools import imtools
import pydot

#download_path = "panoimages"  # set this to the path where you downloaded the panoramio images
#path = "/FULLPATH/panoimages/"  # path to save thumbnails (pydot needs the full system path)

download_path = "D:/computerVision/testpic1"  # set this to the path where you downloaded the panoramio images
path = "D:/computerVision/testpic1/"  # path to save thumbnails (pydot needs the full system path)

# list of downloaded filenames
imlist = imtools.get_imlist(download_path)
nbr_images = len(imlist)

# extract features
featlist = [imname[:-3] + 'sift' for imname in imlist]
for i, imname in enumerate(imlist):
    sift.process_image(imname, featlist[i])

matchscores = zeros((nbr_images, nbr_images))

for i in range(nbr_images):
    for j in range(i, nbr_images):  # only compute upper triangle
        print ('comparing ', imlist[i], imlist[j])
        l1, d1 = sift.read_features_from_file(featlist[i])
        l2, d2 = sift.read_features_from_file(featlist[j])
        matches = sift.match_twosided(d1, d2)
        nbr_matches = sum(matches > 0)
        print ('number of matches = ', nbr_matches)
        matchscores[i, j] = nbr_matches
print ("The match scores is: \n", matchscores)

# copy values
for i in range(nbr_images):
    for j in range(i + 1, nbr_images):  # no need to copy diagonal
        matchscores[j, i] = matchscores[i, j]

#可视化

threshold = 2  # min number of matches needed to create link

g = pydot.Dot(graph_type='graph')  # don't want the default directed graph

for i in range(nbr_images):
    for j in range(i + 1, nbr_images):
        if matchscores[i, j] > threshold:
            # first image in pair
            im = Image.open(imlist[i])
            im.thumbnail((100, 100))
            filename = path + str(i) + '.png'
            im.save(filename)  # need temporary files of the right size
            g.add_node(pydot.Node(str(i), fontcolor='transparent', shape='rectangle', image=filename))

            # second image in pair
            im = Image.open(imlist[j])
            im.thumbnail((100, 100))
            filename = path + str(j) + '.png'
            im.save(filename)  # need temporary files of the right size
            g.add_node(pydot.Node(str(j), fontcolor='transparent', shape='rectangle', image=filename))

            g.add_edge(pydot.Edge(str(i), str(j)))
g.write_png('test.png')

运行结果：

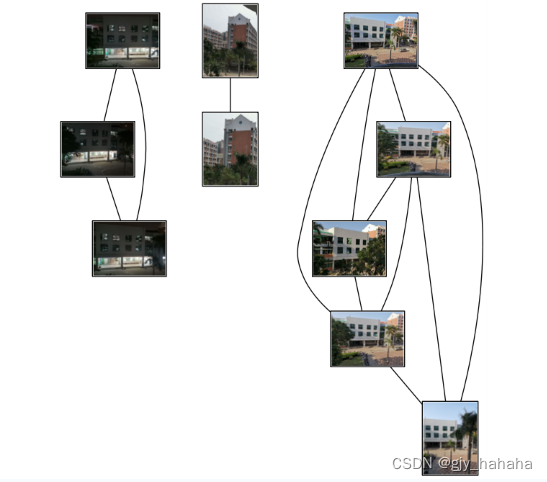
由图所示：无论在光照，尺度变换，部分遮挡等影响下都具有较高的匹配精准度，匹配稳健性高，若用原图像进行匹配，则耗时较长，可考虑将图像进行压缩，提高匹配效率。