第三章 关系数据库设计理论
3.5 BC范式和第三范式
BC范式(BCNF)
-
定义:
关系 R 满足 BCNF
当且仅当:如果 R 中非平凡FD A1,A2,…,An→B 成立,则 {A1,A2,…,An} 是关系 R 的超键。
-
对定义的理解:
-
每个非平凡FD的左边都必须是超键。
(由于超键不一定要最小化,因此可以等价描述为,每个非平凡FD的左边都必须包含键。)
-
-
结论
-
任意一个二元关系属于BCNF。
多个键情况下只要包含任一个键都算满足 BCNF 的条件。
-
-
分解到 BCNF:左右圆法
寻找违反BCNF的非平凡FD A→B ,找到 { A } + \{ A \}^+ {A}+,放到该FD的右端。
然后将关系模式直接分解为两部分:
- 一部分为该FD的左端A和右端属性集
- 一部分为该FD的左端A和该FD未包括的所有属性
如图:

例题:
P51 例3.19 $ {title, year, studioName, president, presAddr} $,
其中,有FD:
? t i t l e , y e a r → s t u d i o n a m e title, year → studioname title,year→studioname
? s t u d i o n a m e → p r e s i d e n t studioname → president studioname→president
? p r e s i d e n t → p r e s A d d r president → presAddr president→presAddr
解:
以 按照违反BCNF的 s t u d i o n a m e → p r e s i d e n t studioname \to president studioname→president 来分解 为例:
计算闭包,得出唯一键是 { t i t l e , y e a r } \{ title, year \} {title,year}。
则 R 1 = { t i t l e , y e a r  ̄ , s t u d i o n a m e } {R_1 = \{\underline{title,year},studioname\}} R1?={title,year?,studioname}
R 2 = { s t u d i o n a m e  ̄ , p r e s i d e n t , p r e s A d d r } {R_2 = \{\underline{studioname}, president,presAddr\}} R2?={studioname?,president,presAddr}
R2 不符合BC范式,故再分解(按照违反BCNF的基本集 p r e s i d e n t → p r e s A d d r president \to presAddr president→presAddr)。
得到 R 3 = { p r e s i d e n t , p r e s A d d r } {R_3 = \{president, presAddr\}} R3?={president,presAddr}
R 4 = { p r e s i d e n t , s t u d i o n a m e } {R_4 = \{president, studioname\}} R4?={president,studioname}
最终结果即为 R1, R3, R4。
第三范式(3NF)
-
定义
如果 R 中非平凡FD A 1 , A 2 , . . , A n → B 1 , B 2 , . . , B m A_1,A_2,..,A_n→ B_1,B_2,..,B_m A1?,A2?,..,An?→B1?,B2?,..,Bm? 成立,
那么或者 {A1,A2,…,An} 是关系R的超键,或者 每个属于 B 但不属于 A 的属性都是某个键的成员。
“主属性” 表示 键包含的属性。
-
对定义的理解
即对于任一非平凡FD,①左侧的属性是 R 的超键 或者 ②右侧的属性是键的属性。
3.6 多值依赖
定义
在关系 R 中,当给定某个属性集合的值时,存在有一组与关系中所有其他属性值相独立的属性值。(以 R ( A , B , C ) R(A,B,C) R(A,B,C) 为例)
-
独立:不能相互决定,相互之间的取值包含所有组合。
-
若给定 R 中属于 A 的各属性的值,
则存在一个属性集 B,B 的值独立于 R 中既不属于A也不属于B的属性集合(也就是C)的值,
则 R 中 MVD A 1 , A 2 , . . , A n → → B 1 , B 2 , . . , B m \text{MVD} A_1,A_2,..,A_n→→ B_1,B_2,..,B_m MVDA1?,A2?,..,An?→→B1?,B2?,..,Bm? 成立,称 A 1 , A 2 , . . , A n A_1,A_2,..,A_n A1?,A2?,..,An? 多值决定 B 1 , B 2 , . . , B m B_1,B_2,..,B_m B1?,B2?,..,Bm? 。
-
对于 R 中每个在 A 上取值相同的元组对 t 和 u,能找到满足下列条件的元组 v:
在 A 属性上的取值与 t 和 u 相同;
在 B 属性上的取值与 t 相同;
在 AB 外的其他所有属性上取值与 u 相同。如图:
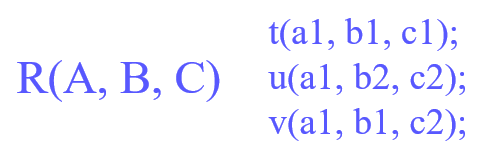
-
对定义的理解
- 设 U 是关系模式R的属性集合,X,Y,Z是 U 的子集,并且 Z = U - X - Y。
R中存在多值依赖 X→→Y ,
当且仅当 对于 R 中的任一关系 r ,给定一对(x,z)值,有一组 Y 值,这组 Y 值仅仅决定于 x 值而与 z 值无关。
-
在 R(U) 的任一关系 r 中,如果存在元组 t,s 使得 t[X] = s[X],那么就必然存在元组 w,v ∈ r,(w,v可以与s,t相同),使得 w[X] = v[X] = t[X],而 w[Y] = t[Y],w[Z] = s[Z],v[Y] = s[Y],v[Z] = t[Z](即交换s,t元组的Y值所得的两个新元组必在 r 中),则 Y 多值依赖于 X,记为 X→→Y。 这里,X,Y是U的子集,Z = U - X - Y。
如图:
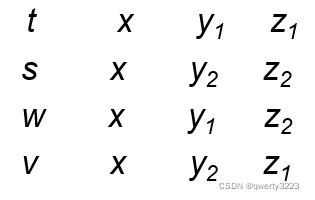
- 设 U 是关系模式R的属性集合,X,Y,Z是 U 的子集,并且 Z = U - X - Y。
平凡多值依赖
- X→→Y,若 Y 包含于 X 或者Z=U - X - Y = ?,则称 X→→Y 为平凡的多值依赖;
- 平凡多值依赖一定成立,之所以称为“平凡的”是因为它并不能定义R上任何重要的或有意义的约束。
多值依赖的推论
-
函数依赖(FD)是多值依赖(MVD)的特殊情况。
这意味着,如果 A 1 A 2 . . . A n → B 1 B 2 . . . B m A_1A_2...A_n \rightarrow B_1B_2...B_m A1?A2?...An?→B1?B2?...Bm?,则 A 1 A 2 . . . A n → → B 1 B 2 . . . B m A_1A_2...A_n \rightarrow \rightarrow B_1B_2...B_m A1?A2?...An?→→B1?B2?...Bm? 也成立。
证明见 PPT
多值依赖的特性
-
MVD 不遵循分解原则。
例如,有 name →→ street city,但是 name →→ street 并不成立。(P63 例3.30)
-
互补规则(对称性)
互换BC符号即可得, 即 Z = U - X - Y,R 中存在多值依赖 X →→Y,则 R 中也存在多值依赖 X →→Z。
第四范式(4NF)
-
定义:
-
在 R 中,若任一 非平凡MVD 成立时,都有 左边是超键 的结论,则 R 属于第四范式。
-
第四范式是 BCNF 的特例,满足 4NF 则满足 BCNF,违反 BCNF 则违反 4NF。
(4NF 包含于 BCNF)
证明见 PPT
-
-
分解到第四范式
若多值依赖左边不是超键,则违反了4NF条件,运用投影分解方法将对应的关系 R 分解为两个关系:
-
含有 A 和 B 的全部属性
-
含有 A 的全部属性和不在 AB 中的全部属性
(与BCNF中的左右圆分解方法非常相似)
-
-
范式之间的联系
- 3NF:任何非平凡函数依赖的左侧是超键或右侧是主属性;
- BCNF:任何非平凡函数依赖的左侧是超键;
- 4NF:任何非平凡多值依赖的左侧是超键;
