[游戏开发]数据结构与算法(十)——查找算法

线性查找（顺序查找）

顺序查找就是最直观的从头开始遍历序列，逐一比对，找到目标元素则返回索引

代码实现

/***
 * 线性查找
 * @author laowa
 *
 */
public class LinearSearch {

	public static void main(String[] args) {
		int arr[] = {0,1,2,3,4,5,6,7,8,9};
		int num=10;
		int index = linearSearch(arr,num);
		if(index==-1) {
			System.out.printf("没有找到%d\n",num);
		}else {
			System.out.printf("%d在数组中的索引为%d\n",num,index);
		}
	}
	
	/**
	 * 线性查找
	 * @param arr 在该数组中查找
	 * @param num 待查数
	 * @return 索引
	 */
	private static int linearSearch(int []arr,int num) {
		//遍历数组，找到目标返回索引
		for(int i=0;i<arr.length;i++) {
			if(arr[i]==num) {
				return i;
			}
		}
		//否则返回-1
		return -1;
	}

}

二分查找（折半查找）

在一个有序序列中，依次将目标数和有序序列中间的数进行对比，

1. 如果目标数更大，表示目标数在右边，向右递归查找
2. 如果目标数更小，表示目标数在左边，向左递归查找
3. 如果两数相等，结束递归，返回索引
4. 一直递归到最后，查找区间没有数据了，表示没有找到，退出递归

代码实现

/***
 * 二分查找
 * @author laowa
 *
 */
public class BinarySearch {

	public static void main(String[] args) {
		int arr[]= {0,1,2,3,4,5,7,8,9,78};
		int num=78;
		int index = binarySearch(arr,num,0,arr.length-1);
		if(index==-1) {
			System.out.printf("没有找到%d\n",num);
		}else {
			System.out.printf("%d在数组中的索引为%d\n",num,index);
		}

	}

	/**
	 * 二分查找
	 * @param arr 目标序列
	 * @param num 目标数
	 * @param left 查找区间的最左边索引
	 * @param right 查找区间的最右边索引
	 * @return 索引
	 */
	private static int binarySearch(int []arr,int num,int left,int right) {
		//如果最左边索引大于最右边索引，则当前查找区间已经没有元素了，没有找到该元素
		if(left>right) {
			return -1;
		}
		//取得中间索引
		int mid = (left+right)/2;
		//如果中间的数大于目标数，则向右递归
		if(arr[mid]>num) {
			return binarySearch(arr,num,left,mid-1);
		}
		//如果中间的数小于目标数，则向左递归
		if(arr[mid]<num) {
			return binarySearch(arr,num,mid+1,right);
		}
		//否则表示中间的数等于目标数，找到了，直接返回中间索引
		return mid;
	}
}

二分查找完善（找出所有的目标数）

/***
 * 二分查找
 * @author laowa
 *
 */
public class BinarySearch {

	public static void main(String[] args) {
		int arr[]= {0,1,2,3,4,5,7,8,9,78,78,78,78,78,78,78,89};
		int num=78;
		List<Integer> indexList = binarySearch(arr,num,0,arr.length-1);
		if(indexList.size()==0) {
			System.out.printf("没有找到%d\n",num);
		}else {
			System.out.println(num+"在数组中的索引为"+indexList);
		}

	}

	/**
	 * 二分查找
	 * @param arr 目标序列
	 * @param num 目标数
	 * @param left 查找区间的最左边索引
	 * @param right 查找区间的最右边索引
	 * @return 索引
	 */
	private static List<Integer> binarySearch(int []arr,int num,int left,int right) {
		//如果最左边索引大于最右边索引，则当前查找区间已经没有元素了，没有找到该元素，返回空集合
		if(left>right) {
			return new ArrayList<>(0);
		}
		//取得中间索引
		int mid = (left+right)/2;
		//如果中间的数大于目标数，则向右递归
		if(arr[mid]>num) {
			return binarySearch(arr,num,left,mid-1);
		}
		//如果中间的数小于目标数，则向左递归
		if(arr[mid]<num) {
			return binarySearch(arr,num,mid+1,right);
		}
		List list = new ArrayList<>();
		//否则表示中间的数等于目标数，找到了，将该数添加到集合中
		list.add(mid);
		//向左查找的索引
		int l=mid-1;
		//向右查找的索引
		int r = mid+1;
		//依次向左找，在当前区间中找到所有和当前值相等的数
		while(l>=left&&arr[l]==num) {
			list.add(l);
			l--;
		}
		//依次向右找，在当前区间中找到所有和当前值相等的数
		while(r<=right&&arr[r]==num) {
			list.add(r);
			r++;
		}
		//返回集合
		return list;
	}
}

插值查找

1. 插值查找算法类似于二分查找，不同的是插值查找每次从自适应mid开始查找，是对二分查找的优化
2. 将二分查找中求mid索引的公式改为：mid=(left+right)/2=left+(right-left)/2改为mid=left+(key-arr[left])*(right-left)/(arr[right]-arr[left]),mid就是插值索引
3. 二分查找是每次都在区间的中间，而插值查找每次回根据序列中值的比例，映射到位置的比例从而自适应的往更靠近目标值的位置划分区间

代码实现

/***
 * 插值查找
 * 
 * @author laowa
 *
 */
public class InsertSearch {

	public static void main(String[] args) {
		int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 11, 11, 13, 14, 15, 16, 17, 18, 19, 20 };
		int num = 20;
		List<Integer> indexList = insertSearch(arr, num, 0, arr.length - 1);
		if (indexList.size() == 0) {
			System.out.printf("%d不在这个数组中", num);
		} else {
			System.out.println(num + "在数组中的位置为" + indexList);
		}

	}

	/**
	 * 插值查找
	 * 
	 * @param arr
	 *            查找的数组
	 * @param num
	 *            查找的数
	 * @param left
	 *            查找区间左边界
	 * @param right
	 *            查找区间右边界
	 * @return 所有满足查找条件的集合
	 */
	private static List<Integer> insertSearch(int arr[], int num, int left, int right) {
		System.out.println("插值查找");
		// 如果左边大于右边，即查找区间没有数，表示没有找到，返回空集合
		if (left > right) {
			return new ArrayList<>(0);
		}
		// 根据当前待查找数值在当前最小值和最大值之间的相对位置，确定插值索引mid
		int mid = left + (num - arr[left]) * (right - left) / (arr[right] - arr[left]);
		// 如果插值索引处的值比当前值大，则向左递归查找
		if (arr[mid] > num) {
			return insertSearch(arr, num, left, mid - 1);
		}
		// 如果插值索引处的值比当前值小，则向右递归查找
		if (arr[mid] < num) {
			return insertSearch(arr, num, mid + 1, right);
		}
		// 左右遍历所有目标数，添加到结果集中
		List<Integer> list = new ArrayList<>();
		list.add(mid);
		int l = mid - 1;
		int r = mid + 1;
		while (l >= left && arr[l] == num) {
			list.add(l);
			l--;
		}
		while (r <= right && arr[r] == num) {
			list.add(r);
			r++;
		}
		return list;
	}

}

对比

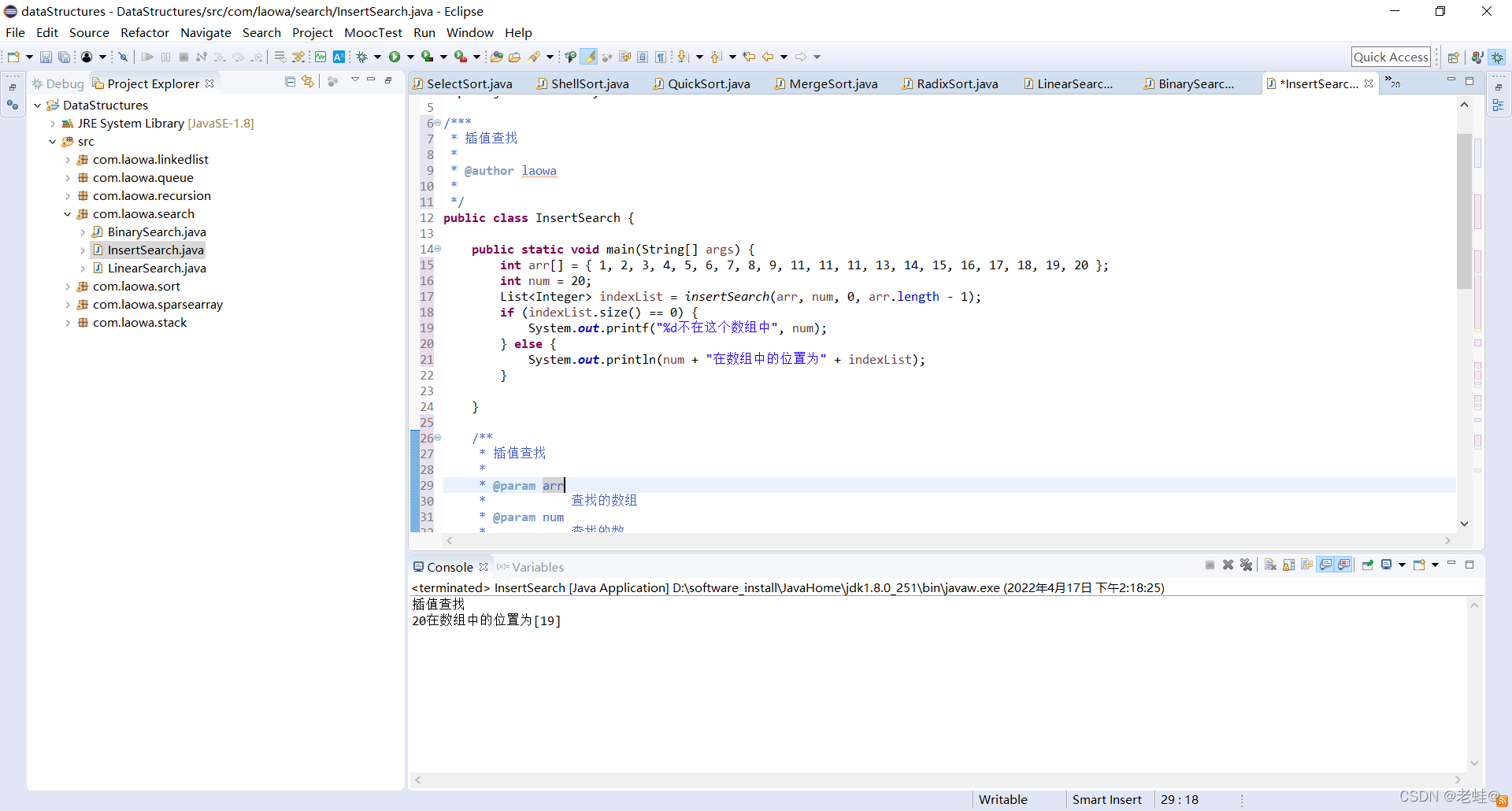
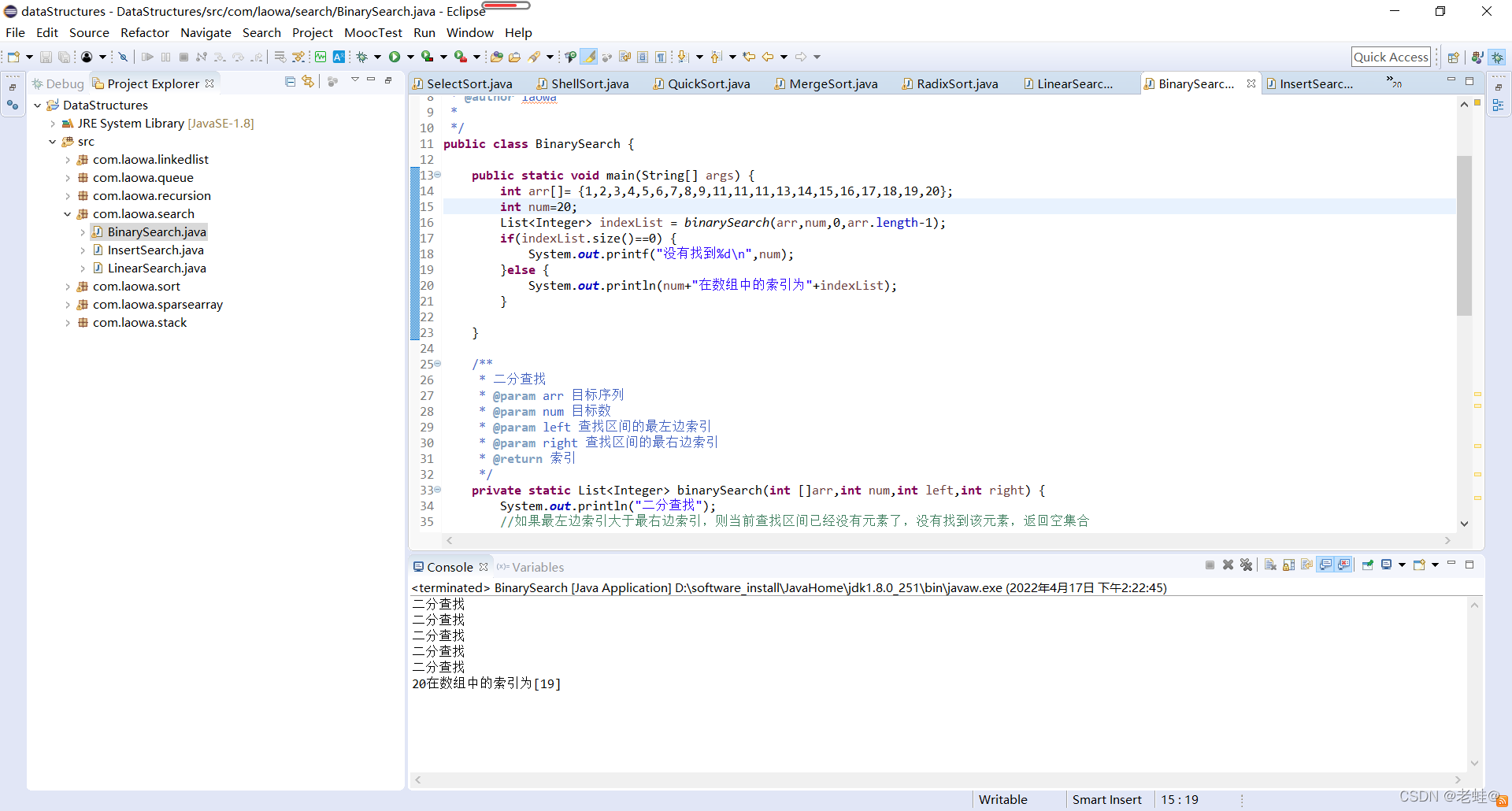
1. 当查找的数靠数组边缘时，二分查找就会查找多次，而插值查找根据自适应找到插值索引，便能更快查找到目标数
2. 对于数据量较大，关键字分布比较均匀的查找表，采用插值查找速度较快
3. 在关键子分布不均匀的情况下，该方法不一定比折半查找好

斐波那契查找（黄金分割查找法）

1. 黄金分割点是指用一点将一条线段分割成两部分，其中短比长等于长比全等于0.618，这个点即黄金分割点，这个比例称为黄金分割比
2. 斐波那契数列{1,1,2,3,5,8,13,21,34,55…}，前两个数字为1，往后每一个数都是前两个数的和，形成的数列即斐波那契数列，数列越往后，相邻两个数的比例无限趋近于黄金分割比

查找原理

斐波那契查找和二分查找、插值查找相似，区别在于改变了中间结点mid的位置，这里mid不在时通过中间或按比例插值得到，而是位于黄金分割点附近 ，即mid=left+F(k-1)-1

1. 由斐波那契数列F(k)=F(k-1)+F(k-2)的性质，可以得到F[k]-1=(F[k-1]-1)+(F[k-2]-1)+1，即只要顺序表长度为F[k]-1则可以将该表分成长度为F[k-1]和F[k-2]的两部分，从而结点位置为mid=left+F[k-1]-1
2. 但顺序表长度n不一定刚好等于F[k]-1，那么需要将原来的顺序表的长度增加到F[k]-1,步骤为先增加k值使得F[k]-1大于n，然后使n+1
   
   

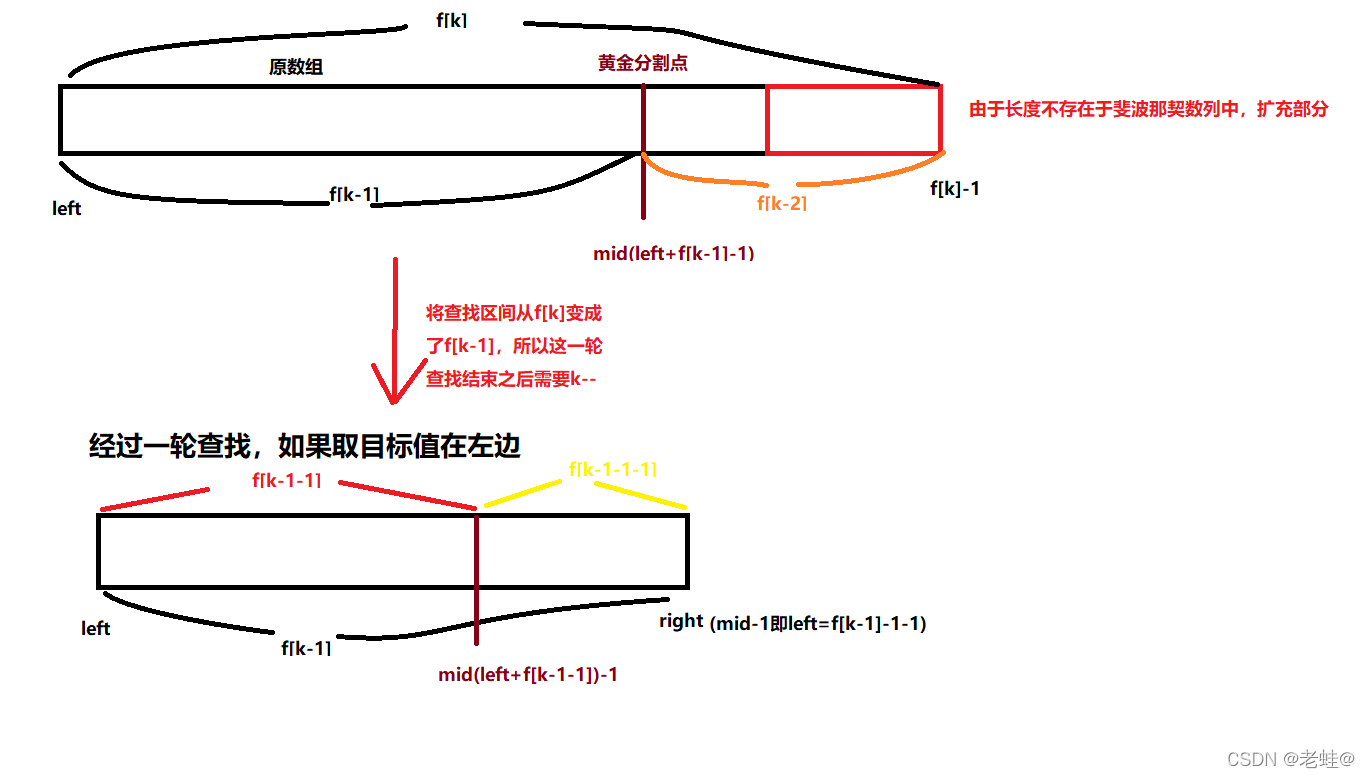
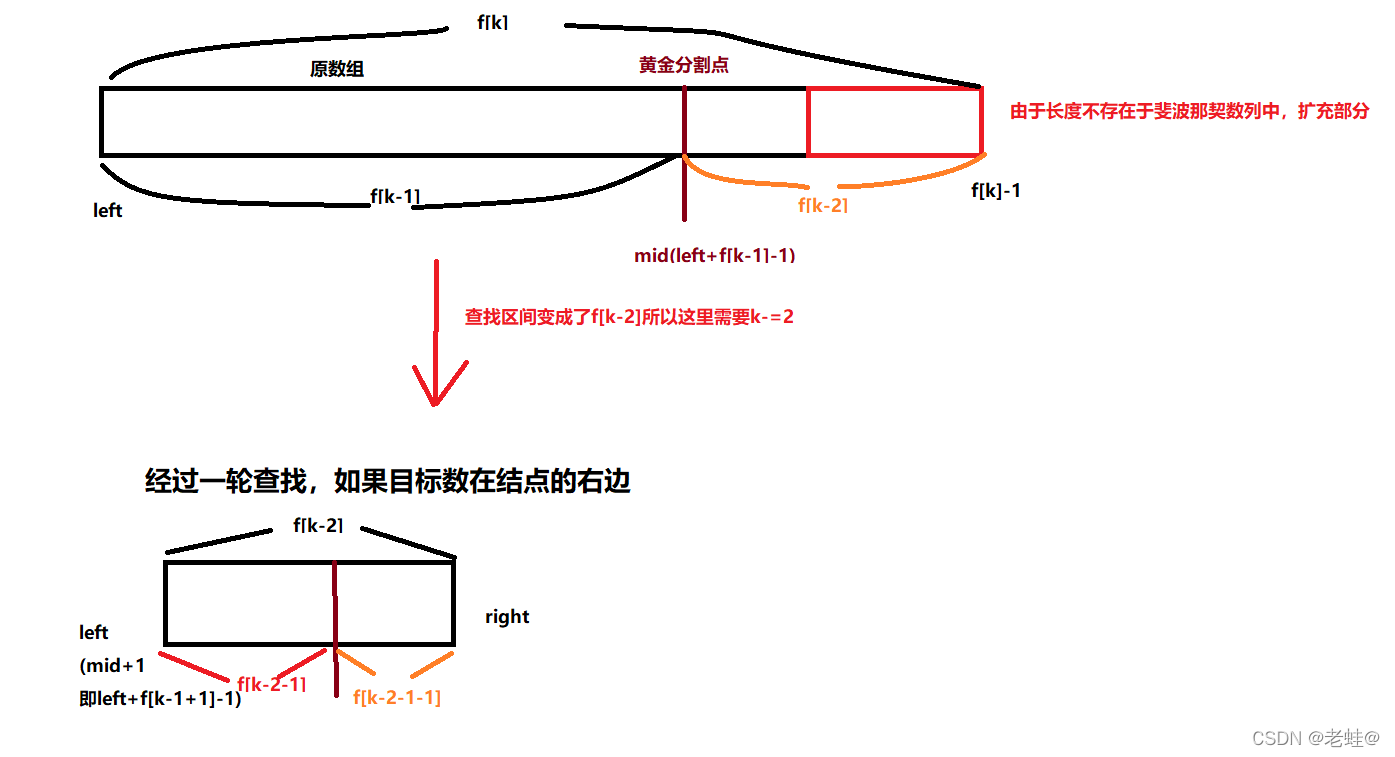
代码实现（递归和非递归两种方式）

/***
 * 斐波那契查找
 * 
 * @author laowa
 *
 */
public class FibonacciSearch {

	public static void main(String[] args) {
		printArray(getFib(10));
		int arr[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 11, 11, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 25, 25,
				25, 255 };
		int num = 25;
		List<Integer> indexList = fibonacciSearch2(arr, num);
		if (indexList.size() == 0) {
			System.out.printf("%d不在这个数组中", num);
		} else {
			System.out.println(num + "在数组中的位置为" + indexList);
		}
	}

	/**
	 * 斐波那契查找，非递归法
	 * 
	 * @param arr
	 *            查找的数组
	 * @param key
	 *            待查找的数
	 * @return 所有目标数的索引
	 */
	private static List<Integer> fibonacciSearch(int arr[], int key) {
		// 查找区间的左边界
		int left = 0;
		// 查找区间的有边界
		int right = arr.length - 1;
		// 斐波那契数列的下表，通过斐波那契数列相邻两个数趋于黄金分割比的性质找到数组中的黄金分割点
		int k = 0;
		// 黄金分割点
		int mid = 0;
		// 获取斐波那契数列
		int f[] = getFib(arr.length);
		// 让当前数组的长度等于斐波那契数列中的某个值，斐波那契数列的前一个值在当前数组中对应的下标就是黄金分割点
		// 在斐波那契数列中找到大于当前数组长度的值
		while (right > f[k] - 1) {
			k++;
		}
		// 创建一个临时数组，因为可能当前数组的长度不是恰好为斐波那契数列中的某个值，那么将数组扩容，放入临时数组中
		int temp[] = Arrays.copyOf(arr, f[k]);
		// 将原数组最后一个数复制到扩容部分，保证数组的有序
		for (int i = arr.length; i < temp.length; i++) {
			temp[i] = arr[right];
		}

		List<Integer> indexList = new ArrayList();
		// 开始分割，直到查找区间没有元素
		while (left <= right) {
			// 找到黄金分割点，此时查找区间的长度为f[k]，即right-left=f[k],黄金分割后，长/全即f[k-1]/f[k]所以黄金分割点长部分的长度为f[k-1]对应数组中的位置即left+f[k-1]-1
			mid = left + f[k - 1] - 1;
			// 如果目标值在结点的左边，则向左分割
			if (key < temp[mid]) {
				right = mid - 1;// 将划分区间定在了结点的左边第一个位置
				k--;// 此时查找区间的长度变成了线段中的长一部分，即f[k-1]所以k自减，下一次找分割点就会找到k-2
			} else if (key > temp[mid]) {
				// 如果目标值在结点的右边，则向右分割
				left = mid + 1;// 将划分区间定在了结点右边第一个位位置
				k -= 2;// 此时查找区间长度变成了线段中短一部分，即f[k]-f[k-1]=f[k-2]，所以k需要减2
			} else {
				// 如果结点在right的右边，表示找到了扩容部分了，扩容部分值都是数组的最后一个值，将结点设置为right
				// 如果结点在right的左边，表示目标值在原数组中间
				mid = mid < right ? mid : right;
				// 根据明确后的mid值左右查找相同值，添加入集合中
				int l = mid - 1;
				int r = mid + 1;
				indexList.add(mid);
				while (l >= left && arr[l] == key) {
					indexList.add(l);
					l--;
				}
				while (r <= right && arr[r] == key) {
					indexList.add(r);
					r++;
				}
				break;
			}
		}
		return indexList;
	}

	/**
	 * 斐波那契查找，递归法
	 * 
	 * @param arr
	 *            查找数组
	 * @param num
	 *            目标数
	 * @return 找到的位置的集合
	 */
	private static List<Integer> fibonacciSearch2(int arr[], int num) {
		// 获取斐波那契数列
		int f[] = getFib(arr.length);
		int k = 0;
		// 让当前数组的长度等于斐波那契数列中的某个值，斐波那契数列的前一个值在当前数组中对应的下标就是黄金分割点
		// 在斐波那契数列中找到大于当前数组长度的值
		while (arr.length > f[k]) {
			k++;
		}
		// 创建一个临时数组，因为可能当前数组的长度不是恰好为斐波那契数列中的某个值，那么将数组扩容，放入临时数组中
		int temp[] = Arrays.copyOf(arr, f[k]);
		// 将原数组最后一个数复制到扩容部分，保证数组的有序
		for (int i = arr.length; i < temp.length; i++) {
			temp[i] = arr[arr.length - 1];
		}
		return fibSearch(0, arr.length - 1, temp, f, k, num);
	}

	/**
	 * 
	 * @param left
	 *            查找区间的左边界
	 * @param right
	 *            查找区间的有边界
	 * @param temp
	 *            扩容后长度满足斐波那契数列的数组
	 * @param f
	 *            斐波那契数列
	 * @param k
	 *            当前查找区间长度对应斐波那契数列中的数的下表
	 * @param num
	 *            目标数
	 * @return 查找到的索引集合
	 */
	private static List<Integer> fibSearch(int left, int right, int temp[], int f[], int k, int num) {
		// 如果左边界大于右边界，表示查找区间没有数据了，返回空集合
		if (left > right) {
			return new ArrayList<>(0);
		}
		// 获得黄金分割点
		int mid = left + f[k - 1] - 1;
		// 如果黄金分割点的数据小于目标数，则向右分割
		if (temp[mid] < num) {
			// left变成mid+1，k向前移动两位
			return fibSearch(mid + 1, right, temp, f, k - 2, num);
		}
		// 如果黄金分割点的数据大于目标数，则向左分割
		if (temp[mid] > num) {
			// right变成mid-1，k向前移动一位
			return fibSearch(left, mid - 1, temp, f, k - 1, num);
		}
		List<Integer> indexList = new ArrayList();
		// 如果结点在right的右边，表示找到了扩容部分了，扩容部分值都是数组的最后一个值，将结点设置为right
		// 如果结点在right的左边，表示目标值在原数组中间
		mid = mid > right ? right : mid;
		int l = mid - 1;
		int r = mid + 1;
		// 将所有相同的值的索引加入数组
		indexList.add(mid);
		while (l >= left && temp[l] == num) {
			indexList.add(l);
			l--;
		}
		while (r <= right && temp[r] == num) {
			indexList.add(r);
			r++;
		}
		return indexList;

	}

	/**
	 * 获取斐波那契数列
	 * 
	 * @param length
	 *            需要获取的个数
	 * @return 数组
	 */
	private static int[] getFib(int length) {
		if (length < 0) {
			System.out.println("长度不能小于0");
		}
		int res[] = new int[length];
		// 如果长度为1，则返回数列{1}
		res[0] = 1;
		if (length == 1) {
			return res;
		}
		// 如果长度为2则返回数列{1,1}
		res[1] = 1;
		if (length == 2) {
			return res;
		}
		// 否则递归获取斐波那契数列
		return fibonacciArray(res, 2);
	}

	/**
	 * 递归获取斐波那契数列
	 * 
	 * @param res
	 *            存储数列的数组
	 * @param t
	 *            当前存储的位置索引
	 * @return 斐波那契数列数组
	 */
	private static int[] fibonacciArray(int res[], int t) {
		// 当前位置已经超过了数组的最大长度，结束递归
		if (t == res.length) {
			return res;
		}
		// 计算当前位置的值
		res[t] = res[t - 2] + res[t - 1];
		// 指针后移
		t++;
		// 递归计算下一位的值
		return fibonacciArray(res, t);
	}

	/**
	 * 打印数组
	 * 
	 * @param arr
	 *            待打印的数组
	 */
	private static void printArray(int[] arr) {
		for (int i : arr) {
			System.out.print(i + " ");
		}
		System.out.println();
	}
}

对比

斐波那契查找和折半查找的时间复杂度相同，而且有时执行次数可能会比折半查找更多，但是斐波那契每轮循环只有减法和赋值操作，而折半查找有除法操作，这可能是斐波那契查找效率略优于折半查找的原因

创作挑战赛

新人创作奖励来咯，坚持创作打卡瓜分现金大奖