[游戏开发] 第四单元用python学习微积分（二十五）三角函数，反向变量替换，配方，三角函数变换表

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 游戏开发 -> 第四单元用python学习微积分（二十五）三角函数，反向变量替换，配方，三角函数变换表 -> 正文阅读

[游戏开发]第四单元用python学习微积分（二十五）三角函数，反向变量替换，配方，三角函数变换表

本文内容来自于学习麻省理工学院公开课：单变量微积分-反向变量替换，配方-网易公开课

一、公式梳理

1、 $sec(\theta) = \frac{1}{cos(\theta)}$ (secant)

2、 $cec(\theta) = \frac{1}{sin(\theta)}$ (cosecant)

3、 $tan(\theta) = \frac{sin(\theta)}{cos(\theta)}$ (tangent)

4、 $cot(\theta) = \frac{cos(\theta)}{sin(\theta)}$ (cotangent)

5、 $sec^2(\theta) = \frac{cos^2(\theta)+sin^2(\theta)}{cos^2(\theta)} =1+tan^2(\theta)$

6、 $tan'(\theta) = (\frac{sin(\theta)}{cos(\theta)})' = \frac{cos^2(\theta)+sin^2(\theta)}{cos^2(\theta)} = \frac{1} {cos^2(\theta)} = sec^2(\theta)$

7、 $sec'(\theta) = (\frac{1}{cos(\theta)})' = \frac{-(-sin(\theta))} {cos^2(\theta)} = tan(\theta)sec(\theta)$

8、 $\int tan(x)dx = \int \frac{sin(x)}{cos(x)}dx$

设 u = cos(x), u' =du = -sin(x)dx

$\int \frac{-du}{u} = -ln(u) +c = -ln(cos(x)) +c$

9、 $\int sec(x) dx$

设 $u = tan(x) + sec(x)$

由公式 6, 7

$du = sec^2(x) + tan(x)sec(x) = sec(x)(sec(x) + tan(x))dx$

$sec(x)dx = \frac{du}{u}$

$\int sec(x) dx = \int \frac{du}{u} = ln(u) +c = ln(tan(x) + sec(x) ) +c$

二、例题

1、 $\int sec^4(x)dx = \int (1+tan^2(x))sec^2(x)dx$

$u = tan(x) ; du = sec^2(x)dx$

$\int (1+u^2)du = u +\frac{u^3}{3} +c= tan(x) + \frac{tan^3(x)}{3}+c$

用定积分做个简单的验算，取值 $\in (0 , \frac{\pi}{3})$ ，结果是符合的

import numpy as np 
from sympy import *
import matplotlib.pyplot as plt 

def DrawXY(xFrom,xTo,steps,expr,color,label,plt):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    for xval in xarr:
        yval = expr.subs(x,xval)
        yarr.append(yval)
    y_nparr = np.array(yarr) 
    plt.plot(xarr, y_nparr, c=color, label=label)    
    
def DrawTrapezoidal(xFrom,xTo,steps,expr,color,plt, label=''):
    width = (xTo - xFrom)/steps
    xarrRect = []
    yarrRect = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    for step in range(steps):
        yval1 =expr.subs(x,xprev) 
        yval2 = expr.subs(x,xprev + width)
        xarrRect.append(xprev)
        xarrRect.append(xprev)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev)
        yarrRect.append(0)
        yarrRect.append(yval1)
        yarrRect.append(yval2)
        yarrRect.append(0)
        yarrRect.append(0)
        area += width * (yval1+yval2)/2
        plt.plot(xarrRect, yarrRect, c=color)    
        xprev= xprev + width
    print('============================')    
    if len(label)!=0:
        print(label)    
    print('============================')
    print('width = ', width)
    print('area = ',area)
    
x = symbols('x')
expr = sec(x)**4
DrawXY (0,np.pi/3,1000, expr, 'c', label='sec(x)',plt=plt)
print(integrate(expr,(x,0,np.pi/3)))
print(tan(np.pi/3)+tan(np.pi/3)**3/3 - tan(0)+tan(0)**3/3)
plt.legend(loc='upper left')
plt.show()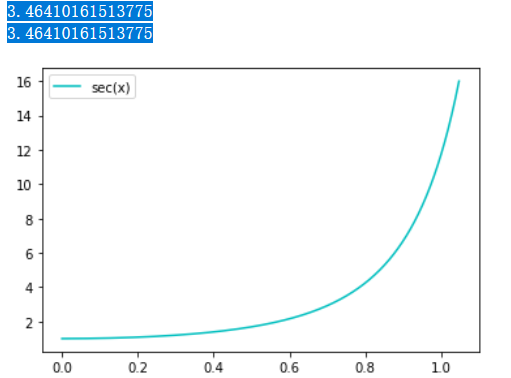

添加图片注释，不超过 140 字（可选）

2、 $\int \frac{dx}{x^2\sqrt{1+x^2}}$

由于tan取值范围从负无穷一直到正无穷，所以可以进行三角替换

设 $tan(\theta) = x 则 dx = tan'(\theta) = sec^2(\theta)d\theta$

另由 $1+tan^2(\theta) =sec^2$

$\int \frac{dx}{x^2\sqrt{1+x^2}} = \int \frac{sec^2(\theta)d\theta}{tan^2(\theta)\sqrt{1+tan^2(\theta)}}$

$= \int \frac{sec^2(\theta)d\theta}{tan^2(\theta)\sqrt{sec^2(\theta)}} = \int \frac{sec(\theta) d\theta}{tan^2(\theta)} = \int \frac{\frac{1}{cos(\theta)}d\theta}{\frac{sin^2(\theta)}{cos^2(\theta)}}$

$= \int \frac{cos(\theta)}{sin^2(\theta)} d\theta$

设 $u = sin(\theta) , du = cos(\theta)d\theta$

$= \int \frac{du}{u^2} = \frac{1}{-u} +c= \frac{1}{-sin(\theta)}+c = -csc(\theta) +c$

还原三角替换

添加图片注释，不超过 140 字（可选）

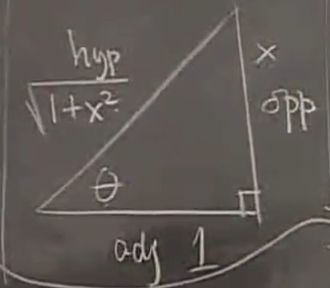
在上图中直角三角形中，设 $\theta$ 的对边长为x，则根据前面假设tan(\theta) = x , 有临边长为1，另斜边长则为 $\sqrt{1+x^2}$

$-csc(\theta) +c = -\frac{1}{sin(\theta)} + c =-\frac{\sqrt{1+x^2}}{x} +c$

或由 $tan(\theta) = x$

$-csc(\theta) +c = -csc( arctan(x)) +c$

用定积分验算下，用梯形法得到的结果和计算出的结果近似。

x = symbols('x')
expr = 1/ (x**2*(1+x**2)**0.5)
DrawXY (2,5,100, expr, 'c', label='',plt=plt)
DrawTrapezoidal(2,5,100,expr,'c',plt, label='1/ (x**2*(1+x**2)**0.5)')
#print(integrate(expr,(x,2,5)))
print('result with arc tangent=', float(-csc(atan(5)) + csc(atan(2))))
print('result = ', -((1+5**2)**0.5)/5 + ((1+2**2)**0.5)/2 )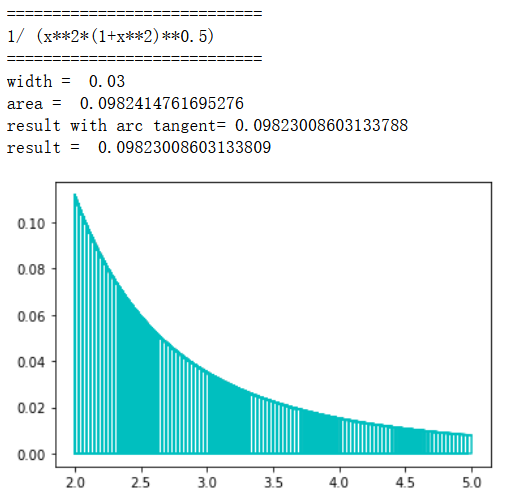

3、如上题去除表达式 " tan(arccsc(x)) " 中三角函数

theta = 45

angle = np.linspace( 0 , 2 * np.pi , 150 ) 
 
radius = 1
 
xarr = radius * np.cos( angle ) 
yarr = radius * np.sin( angle ) 
 
figure, axes = plt.subplots( 1 ) 
 
axes.plot( xarr, yarr, label='radius='+format(radius) ) 


angleInner = np.linspace( theta/180*np.pi , 0 , 150 ) 
xArcInner = radius /10 * np.cos( angleInner ) 
yArcInner = radius /10 * np.sin( angleInner ) 

axes.plot( xArcInner, yArcInner,color='b') 

plt.text(0.18, 0.03, 'θ', fontsize=9)

plt.text(cos(theta)-0.18, -0.08, 'adj', fontsize=9)
plt.text(cos(theta)+0.22, sin(theta)-0.48, 'opp', fontsize=9)
plt.text(cos(theta)-0.3, sin(theta)-0.48, 'hyp', fontsize=9)

axes.set_aspect( 1 ) 
 
x1 = np.cos( theta/180*np.pi )
y1 = np.sin( theta/180*np.pi ) 

xarr1 = [0,1]
yarr1 = [0,0]
plt.plot(xarr1, yarr1,'r',linestyle='-',marker='')

xarr2 = [0,x1]
yarr2 = [0,y1]
plt.plot(xarr2, yarr2,'orange',linestyle='-',marker='')

plt.plot([x1,x1], [0,y1],'green',linestyle='-',marker='')
plt.plot([0,x1], [0,0],'green',linestyle='-',marker='')

plt.text(x1+0.05, y1+0.05, '(cosθ ,sinθ)', fontsize=9)
plt.text(-0.1, -0.1, 'O', fontsize=9)
plt.legend(loc='upper left')
plt.show()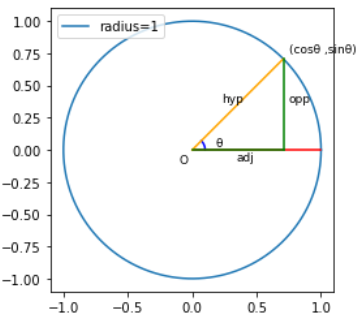

$csc(\theta) = x$

$\frac{1}{sin(\theta)} =x = \frac{hyp}{opp}$

设斜边(hyp)为x，则对边(opp)为1, 临边(adj)为 $\sqrt{x^2 -1}$

$tan(arccsc(x)) = tan(\theta) = \frac{opp}{adj} = \frac{1}{\sqrt{x^2 -1}}$

三、三角替换的小结

1、表

如果积分包含 -- 要做的替换 -- 得到

$\sqrt{a^2 -x^2} -- x = a \times cos(\theta) or x = a \times sin(\theta) -- a \times sin(\theta)$ or $a \times cos(\theta)$

$\sqrt{a^2 +x^2} -- x = a \times tan(\theta) -- a \times sec(\theta)$

$\sqrt{x^2 -a^2} -- x = a \times sec(\theta) -- a \times tan(\theta)$

$\sqrt{a^2 + x^2} = \sqrt{a^2 + a^2tan(x)} = a \times \sqrt{1+tan^2(x)}=a\sqrt{\frac{cos^2(x)}{cos^2(x)}+\frac{sin^2(x)}{cos^2(x)}} =a\sqrt{\frac{1}{cos^2(x)}} =a \times sec(x)$