
Paper: https://openreview.net/pdf?id=C03Ajc-NS5W
Code: https://github.com/divelab/DIG
ICLR 2022 | 从头开始生成三维分子几何结构的自回归流模型
我们考虑了从头开始生成三维分子几何图形的问题。虽然已经开发了多种生成分子图的方法,但从头开始生成三维分子几何图形在很大程度上还有待探索。在这项工作中,我们提出了G-SphereNet,一个新的自回归流模型来生成三维分子几何形状。在这项工作中,我们提出了G-SphereNet,一个新的自回归流模型来生成三维分子几何形状。G-SphereNet采用了一种灵活的顺序生成方案,通过在三维空间逐步放置原子。**我们不直接生成三维坐标,而是通过生成距离、角度和扭转角来确定原子的三维位置,从而保证了不变性和等方差。**此外,我们还提出利用球形消息传递和注意机制进行条件信息抽取。实验结果表明,G-SphereNet方法在随机分子几何生成和目标分子发现方面优于以往的方法。
INTRODUCTION
设计和合成具有理想性质的新分子是药物发现中的一项具有挑战性的任务和化学科学。所有化学分子的搜索空间估计在 1 0 33 10^{33} 1033个左右,因此无法进行彻底搜索。近年来,机器学习方法的进步大大加快了这一领域的进展。许多研究将分子表示为二维分子图,并提出利用深度生成模型自动生成分子图和优化分子性质,如变分自编码器。
然而,从二维分子图中不能获得分子的完整信息,因为三维结构,也称为三维分子几何,是决定许多分子性质的关键。三维分子几何表示原子的三维坐标,对精确预测量子性质具有重要意义。因此,我们认为,生成2D分子图可能不是识别具有某些理想量子特性的新分子的最佳方法。相反,开发一种生成模型,可以从头生成三维分子几何图形,是解决这个问题的一个有希望的解决方案。目前,这一领域仍未得到充分开发。最近,一系列开创性的研究提出了从给定的二维分子图生成三维分子几何图形。这些方法本身不会在给出二维分子图后产生新的分子。
在这项工作中,我们提出了G-SphereNet,一个从零开始生成三维分子几何的生成模型。在G-SphereNet中,三维分子几何图形是通过在三维空间中顺序地放置原子而生成的。原子的三维位置通过生成距离、角度和扭转角度来隐式确定,以确保不变性和等方差特性。我们的工作受到了SphereNet的启发,它使用距离、角度和扭转角度来计算分子的预测表示。此外,G-SphereNet利用SphereNet和注意力机制提取条件信息。实验结果表明,G-SphereNet方法在三维分子几何生成任务上优于现有方法。
BACKGROUND AND RELATED WORK
2D MOLECULAR GRAPH GENERATION
近年来,由于深度生成模型的发展,分子设计与生成问题取得了重大进展。一些方法使用序列模型来生成分子的SMILES字符串表示。其他研究将分子视为图形,其中分子的原子和化学键分别用节点和边表示。这些研究或生成图的节点类型和邻接矩阵,或通过节点和边的顺序添加形成分子图,或由分子基序的连接树组成分子。
然而,这些方法只生成分子的图形结构,而忽略了关键的三维分子几何形状。换句话说,分子中原子的三维坐标是未知的。因此,这些生成模型无法区分空间异构体,即具有相同分子图但具有不同三维分子几何形状的分子。此外,计算分子的一些量子性质,如HOMO-LUMO间隙,需要分子的三维几何形状。因此,当需要空间异构体或量子特性时,这些生成方法不能使用。
3D MOLECULAR GEOMETRY GENERATION FROM SCRATCH
在这项工作中,我们考虑了从头生成三维分子几何图形的问题。设 G = { G j } j = 1 m \text{G} = \{G_j\}^m_{j=1} G={Gj?}j=1m?是一组三维分子几何图形,函数 S ( G ) ∈ R S(G) \in R S(G)∈R计算 G G G的特定量子性质分数。我们考虑定义的两代任务:
- 从 G G G中学习随机生成模型 p θ ( ? ) pθ(·) pθ(?),使模型能够以高概率的 p θ ( G ) pθ(G) pθ(G)对有效的三维分子几何 G G G进行采样。
- 学习一个目标分子发现模型 p θ ( ? ) pθ(·) pθ(?)以最大化(或最小化)期望量子性质分数 E G ~ p θ [ S ( G ) ] E_{G \sim pθ}[S(G)] EG~pθ?[S(G)]。
这个问题在很大程度上还有待探索,只有少数研究试图解决这个问题。G-SchNet利用基于SchNet的自回归模型,依次生成新原子,并将其放置在焦点原子的局域网格点上。另一方面,EDMNet 和3DMolNet 分别利用生成对抗网络(GAN) 和变分自编码器(VAE) 产生原子之间的成对距离。此外,E-NFs提出了一个将flow模型与E(n)等变图神经网络相结合的几何生成模型。它一次性生成所有原子的三维坐标,并定义潜在空间子空间中的先验分布,以确保平移不变性。与这些方法不同的是,我们的方法采用了基于自回归流模型的灵活的顺序生成流水线,可以更有效地捕获三维分子几何密度。
FLOW MODELS
flow 模型定义了参数可逆映射
f
θ
:
z
∈
R
d
→
x
∈
R
d
f_\theta : z \in R^d \rightarrow x \in R^d
fθ?:z∈Rd→x∈Rd, 其中数据点
x
x
x和潜在变量
z
z
z都是随机变量。假设
z
z
z从已知的先验分布
p
Z
pZ
pZ中采样,
f
θ
f_\theta
fθ?是可逆的,我们可以计算
x
x
x的对数似然
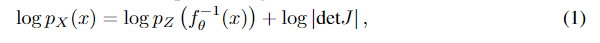
其中 J = ? f θ ? 1 ( x ) ? x J=\frac{\partial f_\theta^{-1}(x)}{\partial x} J=?x?fθ?1?(x)?是Jacobian矩阵。在给定的数据集 x = { x i } i = 1 m x=\{x_i\}_{i=1}^m x={xi?}i=1m?训练flow模型。数据点的对数似然由Eqn.1计算,并通过梯度下降最大化。因此,为了实现有效的训练,需要对 d e t J detJ detJ进行易于处理和廉价的计算。在大多数流动模型中, f θ f_\theta fθ?的常见选择是仿射耦合映射,在这种情况下,由于 J J J是上三角矩阵,计算 d e t J detJ detJ是非常容易的。
flow模型已经在各种生成任务中使用。与VAE和GAN相比,它们允许精确的似然计算,可以更准确地模拟数据密度。由于这些优点,近年来许多研究都将flow动模型用于分子生成任务。一些一次性的方法,如GraphNVP, GRF,MoFlow考虑节点类型和邻接矩阵作为生成目标。另一方面,GraphAF 和GraphDF通过自回归flow模型依次生成节点和边来生成分子图。这些模型比一次性的方法具有更强的图结构建模能力,并在分子图生成任务中取得了最先进的性能。
METHODS
虽然自回归流模型已成功应用于分子图生成任务,但尚不清楚它们是否足够强大,以建模更复杂的三维分子几何。在本节中,我们介绍了G-SphereNet,一种新的三维分子几何生成方法。它采用了一种灵活、有效、高效的基于自回归flow模型的序列生成流水线,既保证了坐标的等方差特性,又保证了似然的不变性。此外,G-SphereNet利用基于表达球面消息传递的图神经网络和多头注意网络提取三维条件信息,进行精确生成。据我们所知,G-SphereNet是第一个基于可能性的自回归生成模型,用于三维分子几何生成。
SEQUENTIAL GENERATION
设 k k k是原子类型的数目。我们使用3D点云 G = ( A , R ) G = (A, R) G=(A,R)来表示含有 n n n个原子的分子的3D几何结构,其中 A ∈ { 0 , 1 } n × k A \in \{0, 1\}^{n \times k} A∈{0,1}n×k是原子类型矩阵, R ∈ R n × 3 R \in R^{n \times 3} R∈Rn×3是原子坐标矩阵。矩阵 A A A中的每一行是one hot向量, A [ j , u ] = 1 A[j,u] = 1 A[j,u]=1表示第 j j j个原子类型为 u u u。
我们认为三维分子几何图形的生成是一个序列决策过程。我们从分子几何图形
G
1
G1
G1开始,起始点有一个碳原子,并通过在每一步添加一个新原子来生成完整的几何图形。具体来说,在第
i
i
i步, 让由前
i
?
1
i -1
i?1步生成的中间三维分子几何图形为
G
i
=
(
A
i
,
R
i
)
G_i = (A_i,R_i)
Gi?=(Ai?,Ri?), 新原子的原子类型
a
i
{
0
,
1
}
k
a_i \{0,1\}^k
ai?{0,1}k由生成模型
g
a
g^a
ga根据潜在变量
z
i
a
z^a_i
zia?生成。然后生成模型
g
r
g^r
gr根据潜在变量
z
i
r
z^r_i
zir?确定新原子的三维笛卡尔坐标
r
i
∈
R
3
r_i \in R^3
ri?∈R3。
g
a
g^a
ga和
g
r
g^r
gr都是中间生成的几何图形的自回归函数。整个顺序生成过程可以用以下方程来描述:
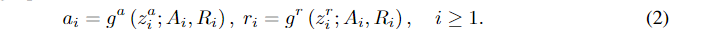
GENERATION WITH AUTOREGRESSIVE FLOW MODELS
我们使用自回归流模型在每一步生成新原子的原子类型
a
i
a_i
ai?。由于原子类型为离散数,我们采用去量化方法,通过加入实值噪声将其转换为连续数

U
(
0
,
1
)
U(0,1)
U(0,1)是(0,1)区间上的均匀分布。为了生成
a
i
a_i
ai?,我们首先从标准高斯分布
N
(
0
,
1
)
N(0,1)
N(0,1)中采样潜变量
z
i
a
∈
R
k
z^a_i \in R^k
zia?∈Rk,然后通过仿射变换将
z
i
a
z^a_i
zia?映射到
a
~
i
\widetilde{a}_i
a
i?。

式中
⊙
\odot
⊙表示元素乘,比例因子
s
i
a
s^a_i
sia?和位移因子
t
i
a
t^a_i
tia?均依赖于从中间几何图形中提取的条件信息
G
i
=
(
A
i
,
R
i
)
G_i = (A_i,R_i)
Gi?=(Ai?,Ri?)。凭直觉,
a
~
i
\widetilde{a}_i
a
i?对于
R
i
R_i
Ri?任何刚性变换应该不变。也就是说,如果我们在3D空间中旋转或平移
R
i
R_i
Ri?,
a
~
i
\widetilde{a}_i
a
i?不应该改变。因此,我们使用对称不变模型来计算
G
i
G_i
Gi?中的
s
i
a
s^a_i
sia?和
t
i
a
t^a_i
tia?,这将在第3.4节中详细描述。得到
a
~
i
\widetilde{a}_i
a
i?后,
a
i
a_i
ai?可以通过取
a
~
i
\widetilde{a}_i
a
i?的argmax来计算,因为
a
i
=
o
n
e
?
h
o
t
(
a
r
g
m
a
x
a
~
i
)
a_i = one-hot(arg max \widetilde{a}_i)
ai?=one?hot(argmaxa
i?)。
然而,我们不能像生成原子类型
a
~
i
\widetilde{a}_i
a
i?那样生成3D坐标
r
i
r_i
ri?。直接用自回归流模型计算
r
i
r_i
ri?,如Eqn 4,既不满足坐标的等方差性,也不满足似然的不变性。首先,很容易发现,如果我们旋转或平移
R
i
R_i
Ri?,那么
r
i
r_i
ri?也需要相应的旋转或平移。形式上,它意味着对于任何正交矩阵
Q
∈
R
3
×
3
Q \in R^{3 \times 3}
Q∈R3×3和平移向量
b
∈
R
3
b \in R^3
b∈R3,如果
r
i
=
g
r
(
z
i
r
;
A
i
,
R
i
)
r_i = g^r(z^r_i;A_i,R_i)
ri?=gr(zir?;Ai?,Ri?),我们有:
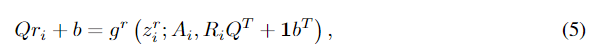
其中1表示所有长度为
i
i
i的向量。如果我们用类似于Eqn (4). 的自回归模型直接计算
r
i
r_i
ri?。i.e.,
r
i
=
s
i
r
⊙
z
i
r
+
t
i
r
r_i = s_i^r \odot z^r_i + t^r_i
ri?=sir?⊙zir?+tir?,然后满足Eqn(5)。
s
i
Q
r
+
b
⊙
z
i
r
+
t
i
Q
r
+
b
=
Q
[
s
i
r
⊙
z
i
r
]
+
Q
t
i
r
+
b
s_i^{Q_r+b}\odot z^r_i +t^{Q_r+b}_i=Q[s^r_i \odot z_i^r]+Qt^r_i+b
siQr?+b?⊙zir?+tiQr?+b?=Q[sir?⊙zir?]+Qtir?+b的正确性对于任何正交矩阵
Q
Q
Q和平移向量
b
b
b都必须保证。然而,很难设计出一种满足这种复杂条件的flow模型。第二,可能性
p
(
r
i
∣
A
i
,
R
i
)
p(r_i|A_i,R_i)
p(ri?∣Ai?,Ri?)对于旋转和平移应该是不变的,因为它们不会改变3D结构。换句话说:
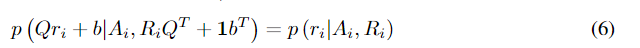
对于任意正交矩阵
Q
Q
Q和平移向量
b
b
b都应该满足。它是由变分定理推导出来的
p
(
r
i
∣
A
i
,
R
i
)
=
p
(
z
i
r
)
∣
d
e
t
?
z
i
r
?
r
i
∣
p(r_i|A_i,R_i)=p(z_i^r)|det \frac{\partial z_i^r}{\partial r_i}|
p(ri?∣Ai?,Ri?)=p(zir?)∣det?ri??zir??∣,设
Q
r
i
+
b
Q_{r_i +b}
Qri?+b?对应的潜变量为
z
i
Q
r
+
b
z_i^{Q_r+ b}
ziQr?+b?。Eqn(4)中的仿射变换不承认
p
(
z
i
r
)
p(z^r_i)
p(zir?)与
p
(
z
i
Q
r
+
b
)
p(z^{Q_r+b}_i)
p(ziQr?+b?)或
?
z
i
r
?
r
i
\frac{\partial z_i^r}{\partial r_i}
?ri??zir??和
?
z
i
Q
r
+
b
?
(
Q
r
i
+
b
)
\frac{\partial z_i^{Q_r+b}}{\partial (Q_{r_i}+b)}
?(Qri??+b)?ziQr?+b??之间有任何关系,因此Eqn(6)不能保证成立。因此,我们不能保证其不变性。
考虑到这些限制,我们建议用对称不变元素来确定新原子的三维相对位置。与G-SchNet类似,我们首先在
G
i
G_i
Gi?中的所有i原子中选择一个焦点原子,作为新原子定位的参考点。然后,模型依次产生距离
d
i
d_i
di?、角度
θ
i
θ_i
θi?和扭转角
φ
i
φ_i
φi?。具体来说,假设焦原子是
G
i
G_i
Gi?的第
f
f
f个原子,首先生成
d
i
=
∣
∣
r
i
?
r
f
∣
∣
2
d_i = ||r_i - r_f||_2
di?=∣∣ri??rf?∣∣2?从焦原子到新原子的距离。然后,如果
i
≥
2
i \geq 2
i≥2,则产生线
(
r
f
,
r
i
)
(r_f,r_i)
(rf?,ri?)和
(
r
f
,
r
c
)
(r_f,r_c)
(rf?,rc?)之间的角
θ
i
∈
[
0
,
π
]
θ_i \in [0,π]
θi?∈[0,π],其中
c
c
c是
G
i
G_i
Gi?中最靠近
f
f
f的原子。最后,如果
i
≥
3
i \geq 3
i≥3,则产生由位置
(
r
f
,
r
c
,
r
i
)
(r_f,r_c,r_i)
(rf?,rc?,ri?)和
(
r
f
,
r
c
,
r
e
)
(r_f,r_c,r_e)
(rf?,rc?,re?)组成的平面之间的扭转角
φ
i
∈
[
π
,
π
]
φ_i \in [π, π]
φi?∈[π,π],其中
e
e
e是离
c
c
c最近但与
G
i
G_i
Gi?中
f
f
f不同的原子。与
a
~
i
\widetilde{a}_i
a
i?类似,
d
i
d_i
di?、
θ
i
θ_i
θi?和
φ
i
φ_i
φi?生成为

其中
z
i
d
,
z
i
θ
,
z
i
φ
∈
R
z^d_i, z^θ_i,z^φ_i \in R
zid?,ziθ?,ziφ?∈R均为从标准高斯分布中采样的潜变量,标度因子
s
i
d
,
s
i
θ
,
s
i
φ
∈
R
s^d_i,s^θ_i,s^φ_i \in R
sid?,siθ?,siφ?∈R和移位因子
t
i
d
,
t
i
θ
,
t
i
φ
∈
R
t^d_i,t^θ_i,t^φ_i \in R
tid?,tiθ?,tiφ?∈R均为
G
i
G_i
Gi?的函数。然后,由相对位置元素
d
i
、
θ
i
、
φ
i
d_i、θ_i、φ_i
di?、θi?、φi?和坐标
r
f
、
r
c
、
r
e
r_f、r_c、r_e
rf?、rc?、re?计算坐标
r
i
r_i
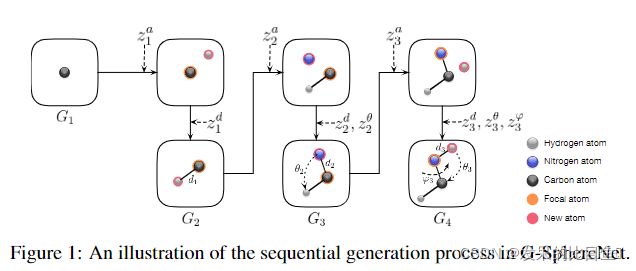
ri?。我们证明了在三维空间中放置新原子的过程可以严格满足Eqn(5)和(6)中的条件。从而同时满足不变性和等方差性质。连续生成过程重复,直到达到原子的最大数目,或者原子级分类器不能选择一个原子作为焦点原子。我们提出的顺序生成方法与SphereNet有关,因为我们的生成目标是SphereNet用来提取特征的3D信息,所以我们将我们的方法命名为GsphereNet。图1给出了G-SphereNet中整个生成过程的说明。
DISCUSSIONS
我们认为我们提出的G-SphereNet方法比以前的三维分子几何生成方法有很多优势。首先,G-SphereNet理论上更容易生成有效的几何图形,因为每个原子的精确三维坐标总是可以得到的。然而,EDMNet和3DMolNet以距离矩阵的形式生成原子的成对距离。没有理论保证所生成的矩阵总是有效的欧氏距离矩阵,或对应于三维空间中的坐标。其次,G-SphereNet中三维位置的生成比G-SchNet中更加灵活。在G-SchNet中,新原子必须被放置在围绕焦点原子的候选网格点之一,但在G-SphereNet中,它可以被放置在焦点原子的任何相对位置。第三,与E-NFs相比,G-SphereNet更加高效有效。E-NFs通过流模型将潜在变量映射到原子的3D坐标。由于坐标不是平移不变的,E-NFs建议通过昂贵的计算操作来获取潜在变量。具体来说,E-NFs首先从潜空间的子空间中定义的先验分布中采样,然后将采样变量通过线性投影映射到潜变量。相比之下,G-SphereNet通过生成距离、角度和扭转角度来获得三维位置,这些自然是平移不变量。因此,G-SphereNet可以避免E-NFs的复杂操作。此外,E-NFs一次生成几何中所有原子的坐标,而G-SphereNet一次获得一个原子的坐标。虽然G-SphereNet可能慢一些,但我们认为,顺序生成方式有助于模型更有效地捕捉原子和几何密度之间的依赖性。实验结果也表明,G-SphereNet可以生成比E-NFs更有效的分子几何形状。
CONDITIONAL INFORMATION EXTRACTION
正如我们在3.2节中提到的,生成原子类型和新原子的3D位置需要在每一步从中间几何结构中捕获条件信息。理想的条件信息应该包含全面的3D几何的结构特点,和任何刚性变换不变量。为了实现这一目标,我们提出使用SphereNet(一种先进的3D图神经网络模型)来捕获条件信息。SphereNet认为输入分子的几何形状是一个方向截断图。用
e
k
e_k
ek?表示第
k
k
k条边的特征,用
v
i
v_i
vi?表示第
i
i
i个节点的特征,SphereNet用球基函数初始化它们,用球消息传递的方式更新它们为
e
’
k
e’_k
e’k?和
v
‘
i
v‘_i
v‘i?:
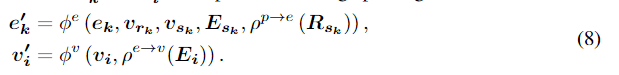
其中
φ
e
φ_e
φe?,
φ
v
φ_v
φv?是更新函数,
ρ
p
→
e
ρ^{p \rightarrow{e}}
ρp→e,
ρ
e
→
v
ρ^{e \rightarrow v}
ρe→v是聚合函数,
r
k
r_k
rk?和
s
k
s_k
sk?是第
k
k
k条边的发送节点和接收节点,
R
s
k
R_{s_k}
Rsk??是
s
k
s_k
sk?的相邻节点的坐标,
E
s
k
E_{s_k}
Esk??和
E
i
E_i
Ei?分别是与节点
s
k
s_k
sk?和
i
i
i相关的边的特征。SphereNet具有强大的三维结构特征提取能力,在多个量子属性预测任务中取得了良好的性能。考虑到这些优势,我们使用SphereNet模型作为主链特征提取器,从中间分子的几何结构中捕获条件信息。
对于输入的分子几何图形 G i G_i Gi?,设从SphereNet计算的节点嵌入为 { h i , j } j = 0 i ? 1 \{h_{i,j}\}^{i-1}_{j=0} {hi,j?}j=0i?1?。在聚焦原子的选择上,我们使用一个以对应的节点嵌入为输入的基于原子的多层感知器(MLP),从分类得分大于0.5的原子中随机选择聚焦原子f。如果从原子型分类器输出的所有分类得分低于0.5,则可以选择没有原子作为焦点,并且顺序生成过程终止。然后,研究了Eqn(4)和(7)的规模和转移因素计算。我们曾经尝试使用参考点 F F F, C C C和 e e e的节点嵌入来计算它们。然而,我们的实验表明,它经常导致新原子在三维空间中的不正确放置。我们认为这是因为节点嵌入只包含局部的3D信息,这对于精确生成新原子的3D位置是不够的。
为了解决上述问题,我们提出通过多头注意网络提取全局特征来增强节点嵌入。正式地,多头注意网络将查询矩阵Q,键矩阵K和值矩阵V作为输入,并通过多头注意机制从输入中提取全局信息:
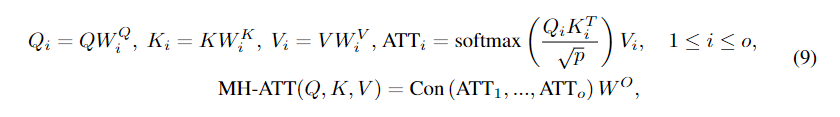
当
C
o
n
(
?
)
Con(·)
Con(?)表示倾斜操作时,
p
p
p是
K
K
K的第二维度的大小,
o
o
o是注意力头的数量,矩阵
W
i
Q
,
W
i
K
,
W
i
V
和
W
O
W^Q_i ,W^K_i,W^V_i和W^O
WiQ?,WiK?,WiV?和WO是所有可训练参数。设
G
i
G_i
Gi? 的节点嵌入矩阵为
H
i
=
[
h
i
,
0
,
.
.
.
,
h
i
,
i
?
1
]
T
Hi = [h_{i,0},...,h_{i,i?1}]^T
Hi=[hi,0?,...,hi,i?1?]T,
s
i
a
s^a_i
sia? 和
t
i
a
t^a_i
tia? 计算为
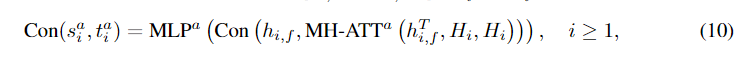
其中
M
H
?
A
T
T
a
MH-ATT^a
MH?ATTa是一个多头注意网络,
M
L
P
a
MLP^a
MLPa是一个多层感知器。对于Eqn(7)的规模和转移因子,我们首先将节点嵌入与原子类型嵌入向量相乘,以包含原子类型信息
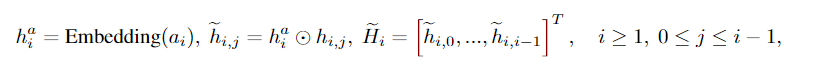
然后将它们计算为

其中
E
m
b
e
d
d
i
n
g
(
?
)
Embedding(·)
Embedding(?)是一个基于查找的嵌入层,
M
H
?
A
T
T
d
MH-ATT^d
MH?ATTd、
M
H
?
A
T
T
θ
MH-ATT^ θ
MH?ATTθ、
M
H
?
A
T
T
φ
MH-ATT^φ
MH?ATTφ都是多点注意网络,
M
L
P
d
MLP^d
MLPd、
M
L
P
θ
MLP^θ
MLPθ、
M
L
P
φ
MLP^φ
MLPφ都是多层感知器。多头注意网络的使用有助于提取更全面的三维条件信息,并在消融研究中被证明大大提高了生成性能。
TRAINING
为了在数据集上训练G-SphereNet模型,我们首先需要将数据集中的每个分子几何拆分为一个原子添加步骤的轨迹。换句话说,需要确定几何中原子的生成顺序和所有相应的焦点原子。由于生成的原子在生成过程中被放置在焦点原子的局部区域,我们提出将Prim算法应用于几何模型来获得训练轨迹。这个过程可以保证采样的焦点原子始终是中间几何中所有原子中新原子的最近邻居。
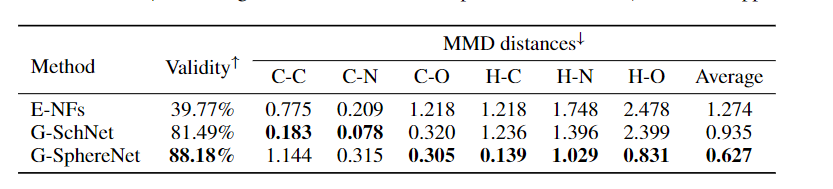
表1:不同方法对随机分子几何生成任务的比较。通过化学键长分布的化学有效性百分比和MMD距离来评价其性能。
↑
\uparrow
↑意味着值越大,性能越好,反之亦然。
对于具有n个原子的三维分子几何G (n > 3),我们最大化其对数似然来训练G- spherenet模型。
具体来说,我们得到生成目标,即每一步要生成原子的原子类型和三维位置,然后计算G的对数似然为
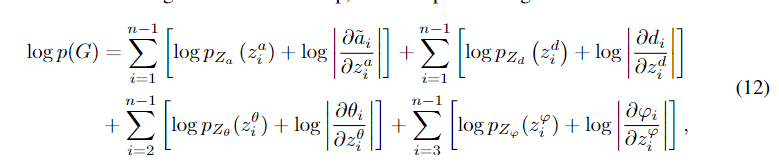
其中潜变量
z
i
a
z^a_i
zia?,
z
i
d
z^d_i
zid?,
z
i
θ
z^θ_i
ziθ?,
z
i
φ
z^φ_i
ziφ?通过在Eqn (4)、(7)中反转映射来计算
p
Z
a
pZ_a
pZa?、
p
Z
d
pZ_d
pZd?、
p
Z
θ
pZ_θ
pZθ?、
p
Z
φ
pZ_φ
pZφ?均为标准高斯分布。此外,G-SphereNet模型中用于焦原子选择的原子分类器是由二元交叉熵损失训练的。如果原子没有价电子被填满,则底真标签为1,否则为0。我们在附录B中详细描述了G-SphereNet的训练和生成算法。


EXPERIMENTS
在本节中,我们将在第2.3节中描述的随机分子几何生成任务和目标分子发现任务上评估提出的G-SphereNet方法。在这些任务中,G-SphereNet可以超过以前的三维分子几何方法,包括G-SchNet和E-NFs。请注意,我们不与最近从2D信息生成3D分子几何图形的方法进行比较,因为它们不能进行目标分子发现(第2.2节)。此外,我们进行了广泛的消融研究,以评估一些设计在G-SphereNet方法中的优势。
RANDOM MOLECULAR GEOMETRY GENERATION
Data. 对于随机分子几何生成任务,我们在QM9数据集上评估G-SphereNet。QM9数据集提供了超过130k的分子,以及通过密度泛函理论(DFT)计算得到的相应的三维分子几何形状。我们随机选取100k个三维分子几何作为训练数据,10k个三维分子几何作为验证数据。为了公平比较,我们的G-SphereNet方法和所有其他方法的模型都使用相同的数据分割进行训练。
Setup. 我们使用化学效度百分比(validity简而言之)来评估G-SphereNet的生成准确性。具体来说,通过Kim & Kim(2015)提出的方法将所有生成的三维分子几何图形转换为分子图,有效性定义为分子图中不违反化学价规则的百分比。除了化学多样性,我们也评估生成的分子几何结构的三维结构精度。我们曾经尝试按照G-SchNet方法计算生成的几何图形和松弛的几何图形之间的坐标差,但我们发现松弛过程涉及到基于DFT的昂贵计算,单个分子几何图形需要数小时的计算。因此,我们建议用最大平均偏差(MMD)来评估键长分布的距离。形式上,我们分别得到了某一类键在生成的几何图形和数据集几何图形中的长度分布,并计算了这两种长度分布与MMD距离之间的统计差异。计算了碳碳单键(C-C)、碳氮单键(C-N)、碳氧单键(C-O)、氢碳单键(H-C)、氢氮单键(H-N)和氢氧单键(H-O)六种最常见化学键的MMD距离。所有的度量都是从10000个生成的分子几何图形中计算出来的。
用于条件信息提取的SphereNet模型的实现基于DIG包的代码。我们使用Adam优化器来训练100个时期的G-Spherenet型号,批次大小为64,学习率为0.0001。有关模型配置和其他训练详细信息,请参阅附录C. 将G-SphereNet与G-SchNet和E-NFs在有效性和MMD距离方面进行了比较,并运行了作者提供的代码,获得了两种基线方法的结果。我们不与EDMNet或3DMolNet进行比较,因为3DMolNet的作者没有提供它们的实现,而且EDMNet模型不能在具有可变原子数的分子几何上进行训练,这阻碍了与G-SphereNet的公平比较。
Model configuration:
Training and generation details
Focal node selection
Results 表1给出了不同方法的性能。我们的G-SphereNet方法达到了88.18%的最高有效性,而E-NFs方法达到了39.77%的低得多的有效性。良好的性能表明,G-SphereNet的序列方式有助于模型捕捉原子间的依赖关系,并更有效地学习分子几何结构的基本化学规律。此外,与G-SchNet相比,我们的G-SphereNet对4种类型的化学键实现了更低的MMD距离,这表明我们的方法可以更准确地模拟分子几何结构的三维结构分布。我们在附录D的图2中可视化了由G-SphereNet生成的一些分子几何图形。
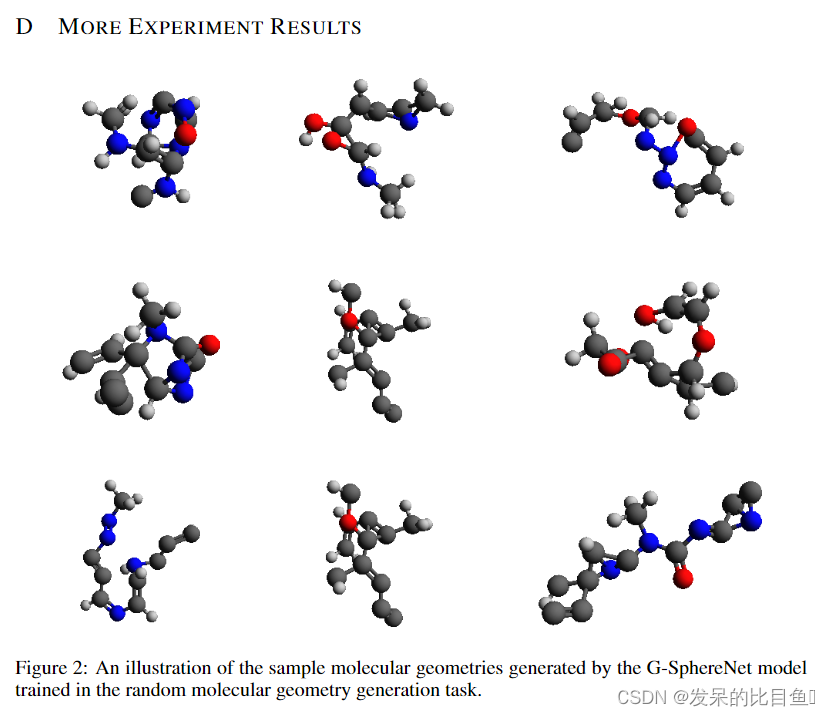
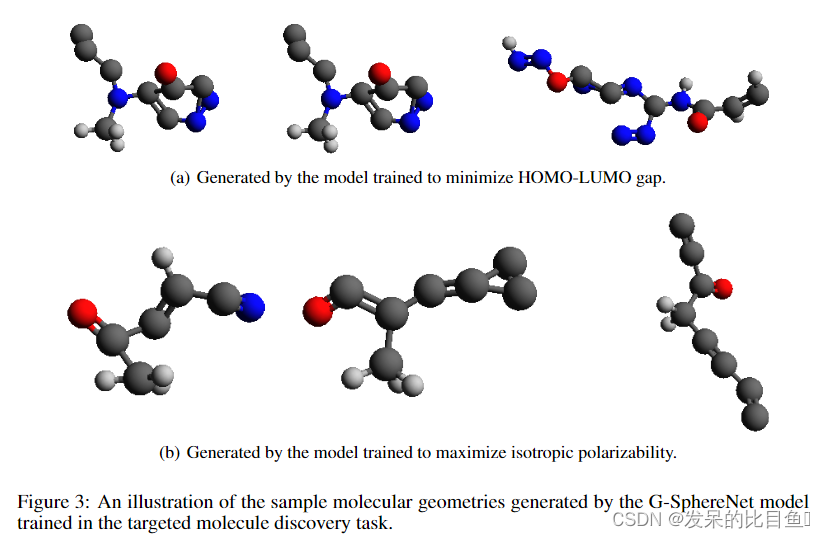
TARGETED MOLECULE DISCOVERY
Setup 在目标分子发现任务中,我们的目标是最大化或最小化期望的全量性质分数。我们进行了两个目标分子发现实验,即最小化HOMO-LUMO间隙和最大化各向同性极化率。在G-SchNet之后,我们在有偏差的数据集上微调了第4.1节中训练的G-SphereNet模型。具体来说,从QM9数据集中,我们收集了所有HOMO- LUMO间隙小于4.5 eV的分子几何图形和所有各向同性极化率大于91 Bohr的分子几何图形。然后,G-SphereNet模型在这两个有偏差的数据集上进行微调,从而分别生成具有低HOMO-LUMO间隙或高各向同性极化率的分子几何形状。关于模型微调过程的细节在附录C中进行了总结。
在这个任务中,我们通过生成的分子几何图形的量子属性分数的三个统计度量来评估性能。具体来说,我们用训练过的模型生成1000个分子几何图形,并过滤掉化学上无效的几何图形。然后,利用PySCF包计算有效分子几何构型的量子性质分数。然后通过三个统计指标对这些量子性能分数进行评估。形式上,我们计算所有属性分数的平均值和最优值,以及属性分数落入良好区域的百分比(简而言之,良好百分比)。好的区域定义为HOMO-LUMO间隙小于4.5 eV,各向同性极化率大于91 Bohr。我们发现E-NFs不能产生足够的化学有效的分子几何形状,并在微调后产生可靠的结果,所以我们在这个任务中只比较我们的G-SphereNet方法和G-SchNet方法。
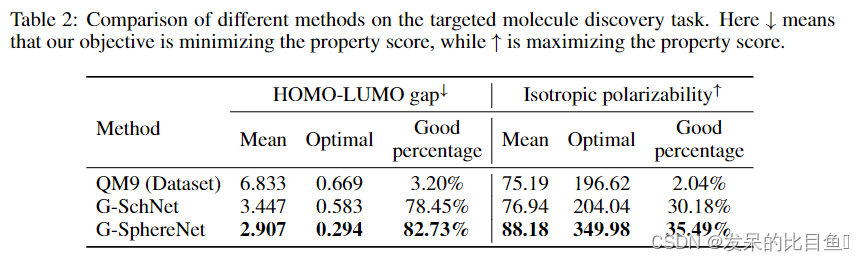
**Results:**表2总结了两个量子特性的目标分子发现结果。对于这两种性质,我们的G-SphereNet在所有指标上都优于G-SchNet,这表明G-SphereNet可以生成更多具有良好性质的分子几何形状。由于两种方法使用相同的预训练和微调管道,我们认为G-SphereNet的更好性能表明它具有更强的搜索具有理想性质的分子几何形状的能力。我们在附录D的图3中说明了一些具有良好性质的生成的分子几何形状。
ABLATION STUDIES
在前面的部分中,我们已经演示了我们的G-SphereNet方法在两个3D分子几何生成任务中的有效性。然而,我们的方法中的一些设计,如使用由多头注意网络提取的全局特征,是否真的能带来良好的性能,目前尚不清楚。因此,我们进行了广泛的消融研究,证明在G-SphereNet的三维条件信息提取中同时使用局部和全局特征,并考虑了距离、角度和扭转信息。外,我们还研究了不同聚焦原子选择方法的影响。在每个消融研究中,不同的G-SphereNet模型根据4.1节的设置进行训练,并通过有效性指标进行评估。表3显示了所有消融研究的结果。
Ablation on local and global feature: 我们比较了只使用本地特性的G-SphereNet变体,即采用SphereNet提取的节点嵌入,仅使用Eqn(10)和(11)中的全局特征,即多头注意网络的输出。
Ablation on 3D information:为了展示使用综合三维信息的优势,我们分别用只考虑距离信息的SchNet和只考虑距离和角度的dimenet++来替代SphereNet。如表3(b)所示,缺失部分3D信息会导致性能下降。
Ablation on focal atom selection:在G-SphereNet中,一个基于原子的MLP和sigmoid函数形成了基于原子的二元分类,发现了价态未满的原子。然后从这些原子中随机选择焦点原子。 相反,Simm等人(2020)提出通过MLP和softmax函数直接选择焦点原子。我们在附录C中详细讨论了两种方法的区别。为了证明我们的方法的好处,我们将其与G-SphereNet变体进行了比较,后者取代了Simm等人(2020)提出的焦原子选择方法。我们用Sigmoid表示我们的方法,用Softmax表示Simm等人(2020)中的方法。如表3?所示,我们的Sigmoid方法可以实现比Softmax方法更好的性能。
CONCLUSION
我们提出了G-SphereNet,一个新的自回归流模型,用于从头生成三维分子几何。G-SphereNet采用顺序生成管道,通过生成相对距离、角度和扭转角度来获得原子的三维位置。该方法灵活、高效,能同时保证系统的等方差和不变性。在序列生成过程中,利用球形消息传递和注意机制提取条件信息。实验结果表明,与以往的方法相比,G-SphereNet方法更精确地模拟了分子的三维几何分布,并具有更强的搜索性能优良分子的能力。将来,我们将应用G-Spherenet将其应用于更复杂的3D结构,例如蛋白质和多体粒子系统。
MORE EXPERIMENT RESULTS
标识的标准和不变性
在G-SphereNet中,在第
i
i
i代步,我们根据模型得到了
d
i
d_i
di?、
θ
i
θ_i
θi?和
φ
i
φ_i
φi?的相对距离。
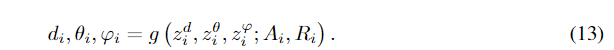
不失一般性,这里我们假设i3。注意g是对称不变的,因为我们使用对称不变的SphereNet 模型提取特征,因此我们有
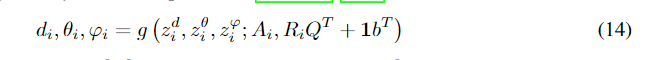
对于任意正交矩阵
Q
∈
R
3
×
3
Q \in R ^{3 \times 3}
Q∈R3×3以及平移向量
b
∈
R
3
b \in R^3
b∈R3。由
d
i
d_i
di?,
θ
i
θ_i
θi?,
φ
i
φ_i
φi?和
r
f
r_f
rf?,
r
c
r_c
rc?,
r
e
r_e
re?计算新原子的
r
i
r_i
ri?坐标。接下来,我们证明了这个生成过程满足等方差和不变性。


