问题引入
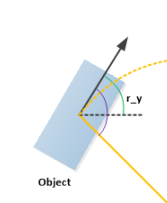
最近在进行kitti数据集可视化操作时,遇到一个问题,数据里面告知了物体框中心点的坐标、宽高(w,l)及旋转角度r_y,然后怎么去确定其各个顶点画出一个框来。
问题思考
关于这个问题,可能刚开始想的是既然中心坐标点告知 ,关键角度和长度也知道,很简单可以直接画坐标系,用三角函数求解即可,可当真正去计算时才发现比较复制,而且非常不利于代码的实现。
于是想到关于旋转用极坐标系计算是否更加简单,解决步骤如下:
确定大致思路
在极坐标系中:
x=pcos@ 1
y=psin@ 2
如果进行旋转只会改变角度@,所以旋转后:
x1=pcos(@+_&) 3
y1=psin(@+_&) 4
将3,4展开并将1,2代入得:
x1=xcos&+ysin& 5
y1=ycos&+xsin& 6
其中&为旋转角度
由此可见只需要知道旋转的角度和原坐标,导入公式5,6就可以计算出旋转后的坐标。
确定旋转本体
在最开始选择的是竖直的本体,W宽是横的,但是这样的话如果往右旋转角度的变化是变小,角度计算时要相减。
 竖直本体向右旋转
竖直本体向右旋转
但是当向左旋转时角度就是往大了变,角度计算要相加。
 竖直本体向左旋转
竖直本体向左旋转
这样就不利于公式的选择和计算,故将本体横放,横着的就是L,这样本体都只是往右进行旋转即可,角度都是往小了变,计算时相减即可。
 横向本体
横向本体
综上所述,采用横向本体更为简便,计算公式如下:
x1=xcos&+ysin& 7
y1=ycos&-xsin& 8
其中&为旋转角度:&=np.pi - r_y
x,y为旋转前的坐标值,在计算初始只考虑旋转,故设中心坐标为原点,所以x,y值可根据其所在的顶点位置由宽高计算得出。当旋转结果计算完成,加上本来中心坐标完成平移,就得到最终结果。
实现代码
def get_corners(x, y, w, l, yaw):
yaw = np.pi - yaw
bev_corners = np.zeros((4, 2), dtype=np.float32)
cos_yaw = np.cos(yaw)
sin_yaw = np.sin(yaw)
# front left
bev_corners[0, 0] = (- l / 2) * cos_yaw + ( w / 2) * sin_yaw +x
bev_corners[0, 1] = (w / 2)* cos_yaw - (- l / 2) * sin_yaw +y
# rear left
bev_corners[1, 0] = ( - l / 2) * cos_yaw + ( - w / 2) * sin_yaw +x
bev_corners[1, 1] = ( - w / 2)* cos_yaw - ( - l / 2) * sin_yaw +y
# rear right
bev_corners[2, 0] = ( l / 2) * cos_yaw + ( - w / 2) * sin_yaw +x
bev_corners[2, 1] = ( - w / 2)* cos_yaw - ( l / 2) * sin_yaw +y
# front right
bev_corners[3, 0] = ( l / 2) * cos_yaw + ( w / 2) * sin_yaw +x
bev_corners[3, 1] = ( w / 2)* cos_yaw - ( l / 2) * sin_yaw +y
return bev_corners
其中输入中心坐标x,y,宽高w,l,角度r_y即yaw,输出一个4*2的矩阵包含4个顶点的坐标。
