Acwing 789: 数的范围
最开始的想法
(1)利用顺序查找确定开始的位置
(2)利用普通的二分查找确定结束的位置
- 正常二分的思路
public static int binartSearch(int [] nums, int target){
int left = 0;
int right = n - 1;
while(left < right){
int mid = left + right >> 1;
if(target == nums[mid]){
return mid;
}else if(target > nums[mid]){
left = mid + 1;
}else{
right = mid - 1;
}
}
}
(3)但是结果显示,某些数据测试下与答案并不相符
- 对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)
对于我的想法,起始位置是找到第一次出现该数的位置是正确的,但是这个终止位置并不是我最开始想的二分查找到的位置,而是最后一次出现该数的位置 ——》所以我的答案是错误的
?? 代码部分:
import java.util.Scanner;
public class Main{
static int [] a = new int [100010];
static int [] nums = new int [10010];
static int flag1 = -1;
static int flag2 = -1;
public static int binarySearch(int low, int high, int target){
while(low < high){
int mid = (low + high) / 2;
if(a[mid] == target){
return mid;
}else if(a[mid] < target){
low = mid + 1;
}else if(a[mid] > target){
high = mid - 1;
}
}
return -1;
}
//设置一个顺序遍历的算法,找到第一次出现该元素的位置
public static int sequentialSearch(int target, int n){
for(int i = 0; i <n; i++){
if(target == a[i]){
return i;
}
}
return -1;
}
public static void main(String [] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
for(int i = 0; i < n; i++) a[i] = sc.nextInt();
for(int j = 0; j < m; j++) nums[j] = sc.nextInt();
for(int k = 0; k < m; k++){
int target = nums[k];
flag1 = sequentialSearch(target, n);
flag2 = binarySearch(0, n -1, target);
System.out.println(flag1 + " " + flag2);
}
}
}
更新后的版本
(1)对于二分查找有两个模板:大于等于模板和小于等于模板
(2)对于一个有序的序列,大于等于和小于等于意味着什么呢?
因为着这个序列中可能没有这个二分搜索的target,而是得到一个比target大或比target小的数。
- 可以用来找一个有序序列中,第一次出现这个元素和最后一次出现这个元素的位置
- 两个模板的代码如下:
寻找左边界的情况:
int left = 0;
int right = n - 1;
while(left < right){
int mid = right + left >> 1;
if(nums[mid] >= target){
right = mid;
}else{
left = mid + 1;
}
}
为什么nums[mid] >= target就要将right = mid呢?
我们可以这样想:当前数的值比目标值大或等于目标值,所以我们要找的目标值的起始位置可能为当前的这个mid位置,也可能在当前位置的左边,所以将右边界更新为当前的mid
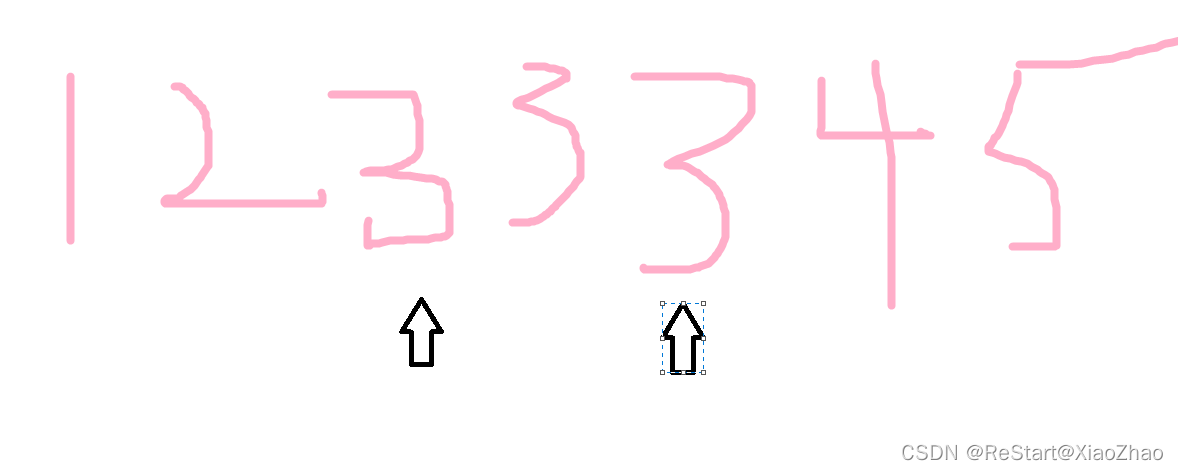
我们要找的就是这两个箭头指向的值
寻找右边界的情况:
int left = 0;
int right = n - 1;
while(left < right){
int mid = right + left + 1 >> 1;
if(nums[mid] <= target){
left = mid;
}else{
right = mid - 1;
}
}
为什么在取中点时要加一呢?(int mid = right + left + 1 >> 1;)
对于整型的除法是一个向下取整的运算,加一是为了避免出现死循环
为什么nums[mid] <= target就要将left = mid呢?
大于等于的思路一样,寻找有边界就是找小于等于的那个数。
如果当前的这个数比目标值小或者等于目标值,那么我们要找的那个最后一次出现目标值的位置就为当前位置或在当前位置的右侧,所以更新左边界为mid
