实际上是纹理映射的知识,所以本文只讨论球体局部直角坐标系转为球面坐标系
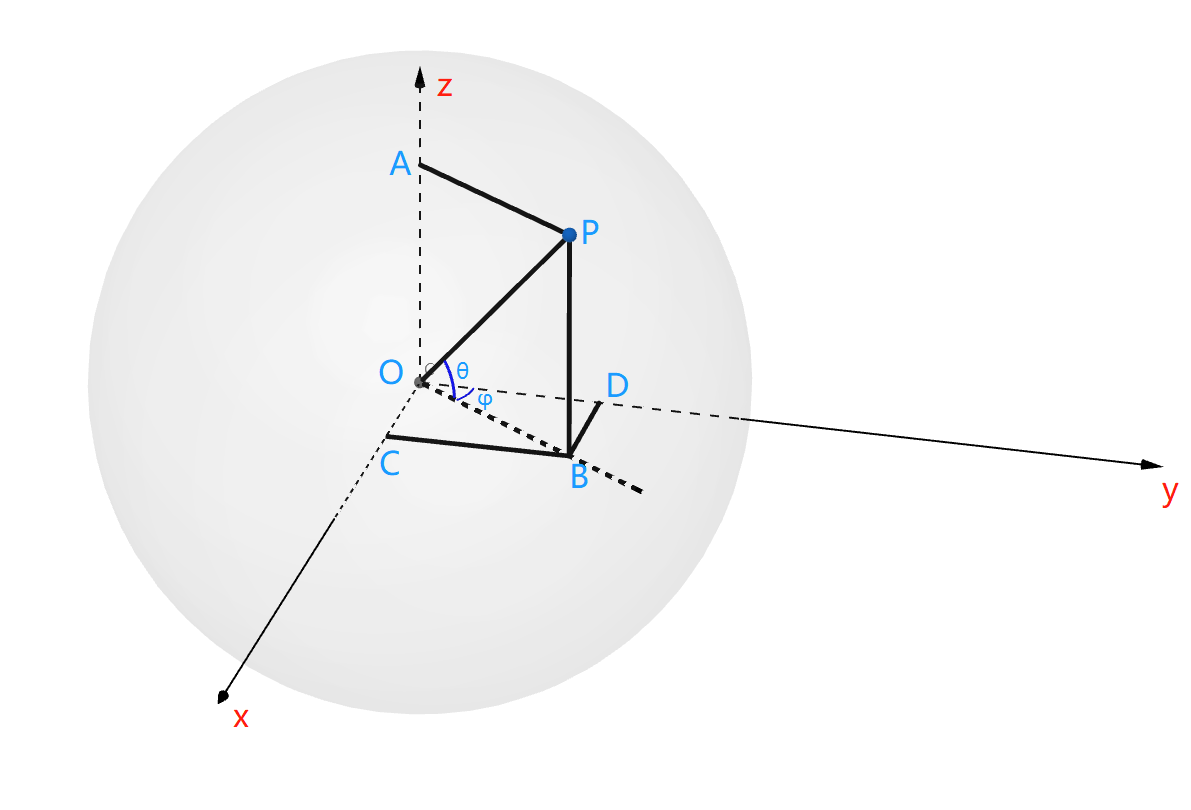
球面坐标系中,P点为单位球上一点,描述P需要2个参数 ( ? , θ ) (\phi,\theta) (?,θ)
\qquad 如果我们定义: ∠ θ ∠θ ∠θ 为 x O z xOz xOz平面上OP与线段OB之间的夹角, ∠ ? ∠\phi ∠? 为线段OP在 x O z xOz xOz平面的投影与y轴正向的夹角,这个夹角不同地方定义的不太一样,但是推导方式没任何区别。在这种定义方式下则他们的取值范围是:
? ∈ ( 0 , 2 π ) θ ∈ ( ? π / 2 , π / 2 ) \phi∈(0,2π)\qquadθ∈(-\pi/2,\pi/2) ?∈(0,2π)θ∈(?π/2,π/2)
根据三角函数公式很简单就能推出直角坐标系与球面坐标系的关系(注:半径 r = 1)
x
=
∣
B
D
∣
=
O
B
?
s
i
n
?
,
O
B
=
1
?
c
o
s
θ
,
∴
x
=
s
i
n
?
?
c
o
s
θ
x = |BD|=OB·sin\phi, OB=1·cosθ ,∴x=sin\phi·cosθ
x=∣BD∣=OB?sin?,OB=1?cosθ,∴x=sin??cosθ
y
=
∣
O
D
∣
=
O
B
?
c
o
s
?
,
O
B
=
1
?
c
o
s
θ
,
∴
y
=
c
o
s
φ
?
c
o
s
θ
y = |OD|=OB·cos\phi ,OB = 1·cosθ,∴y=cosφ· cosθ
y=∣OD∣=OB?cos?,OB=1?cosθ,∴y=cosφ?cosθ
z
=
s
i
n
θ
z = sinθ
z=sinθ
即:
x
=
s
i
n
?
?
c
o
s
θ
y
=
c
o
s
?
?
c
o
s
θ
z
=
s
i
n
θ
\large\color{red} x=sin\phi·cosθ\\ y=cos\phi· cosθ\\ z = sinθ
x=sin??cosθy=cos??cosθz=sinθ
从直角坐标系转到球面坐标系即为上面过程的逆
- 由 x = s i n ? ? c o s θ , y = c o s ? ? c o s θ x=sin\phi·cosθ,y=cos\phi· cosθ x=sin??cosθ,y=cos??cosθ,可知 x y = t a n ( ? ) \displaystyle\frac{x}{y}=tan(\phi) yx?=tan(?)
- ? = a r c t a n ( x y ) \displaystyle\color{red}\phi = arctan(\frac{x}{y}) ?=arctan(yx?)
- θ = a r c s i n ( z ) \color{red}\theta=arcsin(z) θ=arcsin(z)
如果要用球面坐标映射一张图像
(1)球面空间映射到纹理空间
- 球面坐标系目前的范围是 ? ∈ ( 0 , 2 π ) , θ ∈ ( ? π / 2 , π / 2 ) \phi∈(0,2π),θ∈(-\pi/2,\pi/2) ?∈(0,2π),θ∈(?π/2,π/2),
- 对于球面某个点
(
?
,
θ
)
(\phi,θ)
(?,θ)转换到纹理空间的uv坐标为
u = ? / 2 π v = ( θ + π 2 ) π \displaystyle \color{red}\mathbf {\large u =\phi/2\pi} \qquad \large\mathbf{v = \frac{(θ+\frac{\pi}{2})}{\pi}} u=?/2πv=π(θ+2π?)?
(2)纹理空间映射到图像空间
- 第一步中对于从球面空间映射到纹理空间的一个点 ( u , v ) (u,v) (u,v)
- 这个点应该映射到图像空间的某个像素
(
i
,
j
)
(i,j)
(i,j)上
i = u ? ( w i d t h ? 1 ) j = v ? ( h e i g h t ? 1 ) \large\color{red} \mathbf{i = u * (width - 1)}\\ \mathbf{j=v * (height - 1)} i=u?(width?1)j=v?(height?1)
