| [本文大纲] 基础概念篇 ? ??引入 ? ? 光线与介质的作用 ? ? ? ? 光线的传播路径 ? ? ? ? 体积散射和表面光照 ? ? ? ? 光线和介质外观 ? ? 微平面理论 ? ? ? ? 概念介绍 ? ? ? ? 中间向量 ? ? ? ? 能量守恒定律 ? ? ? ? 微平面理论的不足 ? ? 光照计算 ? ? ? ??半球积分 ? ? ? ? 单位光照 ? ? ? ? 反射率方程 ? ? ? ? BRDF与BxDF ? ? ? ? 各向同性和各向异性 ? ? 材质观测 ? ? ? ? 漫反射观测 ? ? ? ? 镜面反射观测 ? ? Disney BRDF ? ? ? ? 概念引入 ? ? ? ? BRDF的参数化 ? ? ? ? Specular BRDF ? ? ? ? Diffuse BRDF ? ? ? ? Sheen ? ? ? ? Clearcoat ? ? Disney BSDF ? ? ? ? 概念引入 ? ? ? ? BSDF的参数化 ????????Diffuse BRDF ? ? ? ? Specular BSDF ? ? ? ? Thin BSDF ? ? ? ? BSSRDF ? ? 环境光照 ? ? ? ? IBL ? ? ? ? 全局光照 ? ? ? ? 完整光照环境 ? ? ue4中的PBR渲染 ? ? ? ? 默认BRDF ? ? ? ? 次表面散射 ? ? ? ? 双面透明材质 ? ? ? ? 预积分皮肤 ? ? ? ? 次表面轮廓 ? ? ? ? 透明涂层 ? ? ? ? 布料材质 ? ? ? ? 头发材质 ? ? ? ? 眼睛材质 ? ? ? ? 环境光照 |
基础概念篇
引入
????????我们之所以可以看见这个缤纷多彩的世界,是因为光线从物体上的某个点进入到了我们的眼睛。而我们之所以能够分辨出一个表面是金属、布料或是陶瓷,是因为我们肉眼看到了它独特的外观。
????????那么,究竟什么是外观(Appearance)呢?更准确来说,我们能够感受到不同的外观,是因为我们感受到了光在介质表面的不同分布情况。也就是说,光进入物体后,由于物体独特的表面属性,光线发生了特定的作用。我们认为这种光在介质上作用形式就是物体的材质(Material)。
光线与介质的作用
? ? ? ? 我们提到了光和介质的不同作用导致了物体的不同的外观。那么,这种作用具体来说,又是什么呢?
????????光线的传播路径
? ? ? ? 当光线照射到物体表面时,我们认为有一部分光线反射(Reflection)出去,也就是改变了传播方向,回到原来的介质中:
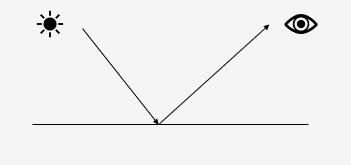
? ? ? ? 这种反射分为不同的情况。一个是镜面反射(Specular Reflection),它描述的是单次反射现象,光线入射后直接反射出去,遵循反射定律(反射角等于入射角)。这更多地发生在金属这样的材质上。
? ? ? ? 另一个是漫反射(Diffuse Reflection),入射光线反射后会发散到各个方向,这是对多次反射的近似模拟,这里的多次反射指光在物体表面或内部经过多次反弹后,又重新从物体表面出射的现象。因此,严格意义上,只有镜面反射属于直接反射,漫反射本质上来自于折射光。
? ? ? ?最后一个特例是逆反射(Refro Reflection),光线会从入射的方向原路直接反弹。逆向反射的发生主要取决于特殊的材质表面形态。
? ? ? ?剩余光线折射(Refraction)进入介质内部:

? ? ? ? 比如光线折射进入水面,这使得我们可以看见水底的东西。? ?
? ? ? ? 通常情况下,入射光线的单次反射会反射到以法线为轴的对称位置上;而折射方向则取决于介质的折射率(IOR)。
? ? ? ? 当光线进入介质中时,由于介质本身有微观粒子,光线与微观粒子作用,可能被吸收(Absorption)了,此时光的强度变弱或颜色发生变化,光能转换为其它类型的能量。如果折射率发生突变(小于光波的距离),光会改变传播方向,也就是发生了散射(Scattering)。如果介质内部有其它形式的能量能够转换为光能(与吸收相反),那么就是一种自发光(Emission)现象。
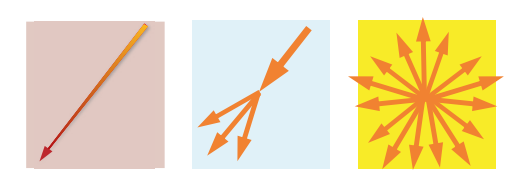
光与物质作用的三种形式:吸收、散射、自发光
????????其中,从当前位置向其它方向散射,称为外散射;从其他方向向当前位置散射,称为内散射。
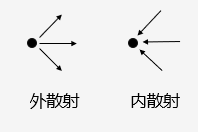
? ? ? ? 另一方面,散射光的分布也有偏向性。如果更多的光沿着前向传播,称为前向散射;如果更多的光沿着与原来相反的方向传播,称为逆向散射。除此之外,还有更多更加复杂的方向分布形态。?在一些比较浑浊的介质(cloudy media)中,散射的光线方向呈现随机性。
????????除了受内部微观分子性质的影响,散射现象还和观察的尺度有关。我们所处的大气因为较远的距离也能呈现出散射的效应。
? ? ? ? 当光线进入介质中时,对于金属而言,折射光会被立即吸收,而对于非金属(电介质/绝缘体)而言,光线会在内部继续行进。这种情况在胶体上比较具有代表性,比如大气、水体等。介质内部吸收和散射的不同比例形成了介质的不同外观:

可以观察到,在几乎无散射也无吸收的时候,介质是清澈的;由于介质中特定颗粒与光线发生了作用,随着散射的强度变大,介质变得浑浊;随着吸收强度的增加,光线中特定分量被吸收,光线变弱,颜色发生改变。
????????在均质介质中,光线的行进方向基本不会发生变化,但它可能具有高吸收性,吸收量会随着光的传播距离增加;而在异质介质中,折射率会发生变化。如果折射率缓慢且连续地变化,则光线会弯曲成曲线。但是,如果折射率发生突变,则光会发生散射,它会分裂成多个方向。
? ? ? ? 均质介质中,如果光线没有太多的被吸收或散射,光线直接从介质另一侧出射:

? ? ? ? 从介质不同侧出射的光线我们通常称为透射(Transmittance),表现在材质上为透光性。
? ? ? ? 比如光线进入玻璃后,大部分又从玻璃另一侧出射,这使得我们可以看见玻璃后面的物体,我们认为玻璃是半透明的。此外,当我们逆光观察像树叶、耳朵这样的薄表面时,会发现表面部分位置透光,这也是一种透射现象。
? ? ? ? 异质介质中,光线可能经过了内部的多次散射,又重新从表面出射,这种出射可以是介质同侧的也可以是异侧的:

? ? ? ? 这种情况通常出现在牛奶、皮肤、蜡烛等半透明物体上,我们称为次表面散射(Subsurface Scattering,3S)。光线在介质内部的散射,由于和微小颗粒发生了作用,可能会产生特定的次表面颜色。
? ? ? ? 表现在材质上为泛光性,比如晶莹剔透的玉石。
? ? ? ? 次表面散射和我们前面提到的漫反射实际上是同一种物理现象。只不过我们通常认为漫反射的入射和出射点在同一位置,而次表面散射的入射和出射点可以在不同位置。此外,入射和出射点是否在同一位置也取决于我们的观测尺度。也就是说,如果一个次表面散射的材质距离较远,那么它将会呈现漫反射的外观;如果近距离观测一个漫反射的材质,那么它也可以表现出次表面散射的外观。

我们认为绿色圆圈内是一个足够小的距离,假如光线进入和离开的间距分布在这个范围内,我们就近似认为入射点等于出射点?,我们把上图绿色区域的距离称为散射距离。

? ? ? ? 体积散射和表面光照
? ? ? ? 另外,在这里需要澄清的是,当我们在讨论胶体的时候,我们想要强调的是光线与介质微观颗粒的相互作用。当我们讨论次表面散射的时候,想强调的是光线在介质内部经过散射后出射这一过程。
? ? ? ? 这也就意味着,在某些情况下,我们会关注在光线在介质内部的行进路线,包括它在某个位置散射或是吸收的状态,这通常用于体积散射(Volumetric Scattering)的计算,比如大气颜色的计算,会使用光线步进(Ray-Marching)来模拟真实的光照计算;
????????而在另外一些情况下,我们会忽略光线在介质内部的传播路径,比如皮肤,我们更关心反射的光线以怎样的贡献比例分布到表面,比如鼻翼、眼角的散射强度是否存在差异。这一部分我们可以将其视为表面光照。
? ? ? ? 光线与介质外观
? ? ? ? 我们已经了解到了光线在介质中的传播路径,包括了从介质表面反射和折射进入介质内部。接下来我们来考虑这样的一个问题,光线的不同传播形式造成了怎样不同的外观。
? ? ? ? 首先再次明确一点,我们之所以能够看见物体,是因为有光线进入了我们的眼睛。只有那些最终被反射(或者透射)出来的光线,才是我们需要关心的。
? ? ? ? 因此,我们能够观察到不同材质呈现不同的颜色,是因为其它部分的波长都被吸收了,只有特定颜色的波长被反射出去,如下图红色的苹果就是因为把红光反射出去,我们才能观测到苹果是红色的。

? ? ? ? 此外,我们还能解释天空为什么是蓝色的。太阳光经过大气层时,其中的部分蓝光发生了明显的瑞利散射而布满了整个天空,使得天空看起来是蓝色的;而其余部分的光线直射穿过大气,仍然呈现为白光。
? ? ? ? 从光学性质来看,我们通常把物质分为金属、电介质和半导体。在PBR中我们通常只考虑金属和电介质。
????????金属表面是具有光泽的,这是因为金属晶体内含有自由电子,而自由电子可以把所有频率的可见光快速反射出去,F0(垂直入射的反射比例)可达50%到100%,因此我们能看到大部分金属表面呈现银白色或刚灰色的光泽。对部分金属而言,由于还吸收了不同波长的光线,可能会呈现特殊的金属色,比如黄色的金子,赤红色的铜。

金属所有可见的颜色都来自于镜面反射,折射进入金属的光会被立即吸收,因而不会发生漫反射或是次表面散射现象。如图,特殊的金属可能会呈现特别的颜色
? ? ? ? 我们在金属表面除了能够观察到金属本身的色泽,还能观察到来自外部场景的反射颜色,这来自于环境光照。反射的图像由于金属的平整程度可能会清晰或模糊,表面越不平整,光的反射方向越不规则,这就导致反射图像的模糊。同理,表面的不平整也会导致反射高光的模糊。
? ? ? ? 电介质是一种绝缘体,由于内部没有具有强反射性的自由电子,只有较少光线反射出去,F0(垂直入射的反射比例)约在2%~7%之间,绝大多数不会超过4%。其余光线得以折射进入介质内部,折射的光线被吸收或散射出去,形成了漫反射或次表面散射的外观。

如图,大部分电介质的反射率都处在一个非常低的范围内
?????????像这种观察到的直接光入射到表面产生的颜色,我们通常称为反照率颜色(Albedo Color),即反射能量和入射能量的比例。对于金属来说,它是镜面反射产生的颜色;而对于非金属而言,它是漫反射产生的颜色。
微平面理论
? ? ? ? 概念介绍
????????当我们在讨论介质表面“光滑”或是“粗糙”的时候,我们实际上描述的是物体的微观属性,即介质在微观尺度的光学平坦程度。
? ? ? ? 我们认为完全光滑的表面是不存在的,像这种理想中完全平坦的表面,我们称为光学平坦表面(Optically flat surface)。光学平坦表面具有一个特性,它可以准确的把光照分为反射和折射两部分。
? ? ? ? 虽然不存在理想光学平面,但是,我们可以将表面视为由大量微小的光学平面组成,那么表面的外观是具有不同表面方向的多个点的聚合结果,每个点将入射光反射到稍微不同的方向,这就是微平面理论。
? ? ? ? 微平面理论所定义的微观的存在尺度小于我们的观察尺度,但明显大于可见波长的尺度,因此每个表面点可被视为光学平面。微平面仅适用于单次反射的推导。

? ? ? ? 我们可以使用法线来描述微平面的方向,因此,微平面的形态就等价于微平面法线的形态。
????????这种表面的不规则性小于像素(pixel)的层级,因此我们难以直接为其建模,因此我们选择从统计学的角度来模拟它的聚合结构,也就是用法线分布(Normal Distribution)来描述微平面的外观形态。微观法线分布有着紧密或是松散的形态,可能在某些方向上表现出偏向性,不同的表面法线分布对物体外观有着很大的影响。

对于宏观上光滑的介质,不同法线分布对介质的外观有着很大的影响
? ? ? ? ?上图体现了微平面法线分布对介质外观的影响。一方面,反射光线较为集中的地方会形成高光,不同的集中程度导致了不同的高光外观;另一方面,表面越粗糙,反射就越模糊,因为表面方向与整体宏观表面方向的分歧更大(上图中下一排)。
? ? ? ? 中间向量
? ? ? ? 我们描述微平面的统计属性的时候,往往会借助中间向量,或者说半向量(half vector)来描述,我们有时候也将其称为微平面法线。
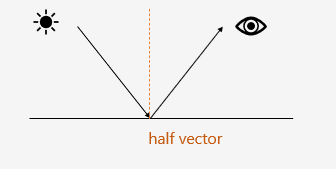
????????中间向量即光线和视线向量的中间向量。中间向量有一个特殊的特性,即当微平面法线和中间向量一致时,反射方向刚好和视线方向重合。?
????????能量守恒定律
? ? ? ? 微平面理论准遵循能量守恒定律,出射光线的能量不会超过入射光线的能量。
? ? ? ? 这种的能量守恒体现在:
? ? ? ? ① 反射的光线和折射的光线能量总和近似小于等于入射光线的能量;
? ? ??? ② 镜面反射的区域越集中,强度也就越高;反之,镜面反射的区域越大,也就越昏暗;
? ? ? ? 逆向反射和微平面
? ? ? ? 一些特殊的微平面结构会导致逆向反射的发生,也就是入射光直接从原路径反射回去:
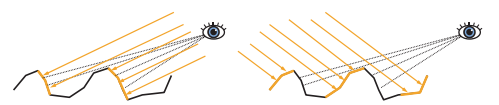
如图,是高散射具有逆向反射性质的微平面。对于具有逆向反射特性的材质,我们从特定方向能观察到明亮的外观,而其余方向则比较暗淡。如左图,视线和灯光方向接近时,观察到明亮的外观,视线和灯光方向有较大差异时,观察到暗淡的外观。
????????如果微观几何不规则性大于次表面散射距离,则微平面表面不规则的遮挡部分会引起逆行反射效应。这主要发生在粗糙度较高的电介质上。
? ? ? ? 微平面理论的不足
? ? ? ? 微平面理论在模拟中存在一些缺陷,主要体现在以下几个方面:
? ? ? ? 一是微平面理论没有考虑波动光学,我们将光视为光线而不是在波中传播。这使得我们无法为与光的波性相关的光学现象建模,比如衍射和薄膜干涉。
? ? ? ? 二是微平面理论仅模拟了统计分布的结果,它认为随着视线变化微观几何的法线可见分布是不会发生变化的,这会导致部分微平面拟合的不准确性,如下图。

图中微平面凸起部分是光滑的,凹陷部分是粗糙的。随着观察方向的变化,看到的表面属性会发生变化。上图第一排观察角度较高时,看到的是粗糙的表面,而第二排观察角度较平时,看到的是光滑的表面。
光照计算
? ? ? ? 在光照计算中,有多种辐射量用来衡量光照属性。
? ? ? ? 我们把一个光源输出的所有能量称为辐射通量(Radiant flux),光源投射到每单位立体角的能量称为辐射强度(Radient Intensity),光源投射到每单位立体角和单位表面的能量称为辐射率(Radiance)。

? ? ? ? 计算投射到介质表面某一点的光照,实际上就是计算该点接收到的所有光照的总和。我们称之为辐照度(Irradiance)。
????????半球积分
? ? ? ? 接下来我们来考虑对于某一点所有可能的光源分布情况。
? ? ? ? 我们认为如果光照方向和当前点的法线角度超过90度,那么该光线是不可见的。因此,对于特定点p,我们可以认为入射光线分布在以点p为球心,点p的法线为中心轴的半球上。

? ? ? ? 因此,如果我们要计算某一点的光照结果,我们需要累加所有反射到该点的入射光产生的影响。由于所有可能反射到该点的入射光分布在反射点的半球区域,因此该过程等价于在半球区域对所有入射光方向进行积分。
? ? ? ? 我们不总是需要积分,一般来说,有以下一些情况:
? ? ? ?① 对于直接入射光,直接计算它对当前点的贡献即可;
? ? ? ?② 对于环境光,由于它没有特定的方向,而是来自四周,需要我们对所有可能的入射光方向进行积分;
? ? ? ? 单位光照
????????让我们来考虑漫反射的一种理想情况,光线均匀地反射到半球的各个方向。假设光线的辐射通量为L,投射到每个位置的辐射率为l,点的法线为n,法线所在的半球空间为Ω,法线与视线方向的夹角为θ,那么我们沿着半球dw积分,可得:
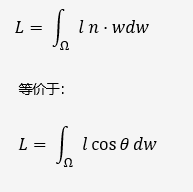 ? ? ? ???
? ? ? ???
? ? ? ? ?这里的半球积分可以转化为极坐标的双重积分来计算。求解后可得:
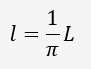
? ? ? ? ?我们可以认为1/PI就是对光照进行归一化之后的结果,我们会经常在光照计算中看到PI系数的乘除,它就是由余弦的球面积分推导出来的。
? ? ? ?反射率方程
? ? ? ? 现在我们已经对光照的基本概念有了一定的了解,接下来我们来讨论如何计算在特定观察方向下,观测到的介质表面某一点的光照结果,也就是我们所说的反射率方程。
????????我们在前面提到辐射率是光源投射到介质某一点的光照量。这里的辐射率并不等于我们观测到的光照结果,我们还需要考虑到两点:
? ? ? ? ① 投射到介质表面的光线可能有一部分进入了介质内部,而只有剩余的光线会反射出来;
? ? ? ? ② 反射出来的光线可能有不同的反射方向,真正进入我们眼睛的光线取决于有多少比例反射光线的反射方向等于当前视线;
? ? ? ? 这种在特定入射和观察方向下,介质表面某一点反射光线和入射光线比例,我们将其称为贡献程度,这种贡献程度可记为f(l,v)。
? ? ? ? 因此,最终得到的反射率方程应为:
????????![]()
? ? ? ? 其中,f为贡献程度,Li为辐射率,l为入射光方向,n为法线。?
? ? ? ?BRDF与BxDF
????????我们可以使用BRDF(双向反射分布函数)来描述贡献程度f(l,v)。它描述了特定光照方向和观察角度下某一点上,反射光线和入射光线的比例。它具有两个性质:
? ? ? ? ① 遵循能量守恒定律,反射光线不会超过入射光线,即BRDF的值不会超过1;
???????? ?
?
? ? ? ? ② 遵循交换律,理论上我们交换 l 和 r 参数能得到同样的结果(但在我们近似的计算中不一定遵循):
????????![]()
????????原则上,BRDF仅考虑表面上方的光线,即我们前面提到的半球分布,换句话说,点积n·l和n·v必须都是非负数。理论上不应出现背向视线的光照输入,但在我们使用插值法线或法线映射可能产生这种情况。可以通过将n·v clamp为0或使用其绝对值来避免对n·v的负值评估BRDF。
?? ? ? ? 分布函数是一种统计学的概念,类似的我们所熟知的概念就是正态分布。它反映了光照在不同入射和出射角度的情况下分布的情况。
? ? ? ? 对于比较粗糙的介质表面,可能多个位置都能得到强度较低的结果,那么它的分布函数就会表现为一个较为平缓的结果;而对于比较光滑的机制表面,只有较为集中的像素点位置能够得到比较大的值,那么它的分布函数的走势就会相对尖锐。

BRDF是一个二维的分布函数,它可以可视化为上图中的形式。
? ? ? ? 当我们在讨论BRDF的时候,我们仅仅考虑了光线接触物体表面反射后的分布情况。
????????扩展来看,我们还有其它用于描述贡献程度的分布函数:
| 名称 | 名称 | 描述 | 应用 | 备注 | |
| BRDF | 双向反射分布函数 | Bidirectional Reflective Distribution Function | 反射光和入射光的比例 | 不透明物体 | |
| BTDF | 双向透射分布函数 | Bidirectional Transmittance Distribution Function | 透射光和入射光的比例 | 透明度较高物体 | |
| BSDF | 双向散射分布函数 | Bidirectional Scattering Distributed Function | 散射光和散射光的比例 | 透明度较高物体 | BSDF = BTDF + BRDF |
| BSSRDF | 双向散射表面反射率分布函数 | Bidirectional Scattering Surface Reflectance Distributed Function | 次表面散射光和入射光的比例 |
????????这一类分布函数我们统称为BxDF。我们可以这样理解这些分布函数的含义:
? ? ? ? 我们在前面提到光线照射到介质表面后,最终有两个去向,一个是反射离开介质,另一个是折射进入介质。我们使用BRDF来描述反射的贡献结果,而使用BTDF去描述折射的贡献结果,这两者实际就基本涵盖了所有光照的去向,我们统称为BSDF(参见Disney BSDF)。
????????特别的,我们使用BSSRDF来描述次表面散射,它本质上也是一种反射,但由于出射和入射点的不一致带来了计算上的复杂度,我们往往将该分量独立出来计算。
????????各向同性和各向异性
? ? ? ? 当入射光和反射光保持相对角度不变,绕着法线旋转时,如果BRDF的性质不变,那么这个材质就是各向同性材质,也就是说,各向同性材质具有旋转对称的特性。而如果绕着法线旋转时,BRDF的性质会发生变化,那么该材质为各向异性材质。
? ? ? ? BRDF的结果由入射光和出射光方向确定,每个方向可由两个角度参数化,因此,总共可由四个角度参数化。特别的,对于各向同性的参数,由于其旋转对称性,我们仅需三个角度就能对其进行参数化。

BRDF的角度参数化,其中每个方向可由两个角度来确定;如,入射光可由φi和θi确定,出射光可由φ0和θ0确定
? ? ? ? 大部分材质都具有各向同性的表面统计数据,只有小部分材质的微观结构具有明显的各向异性结构,比如头发、拉丝金属等。

各向异性的拉丝金属
?? ? ? ? 各向同性和各向异性一个明显的特征表现在高光的形状上。比如各向同性的球体高光可能表现为一个圆形或椭圆形,而各向异性的高光可能表现为一个环形。
材质观测
? ? ? ? 为了能够近似模拟材质的光照效果,我们首先需要观测现实世界中材质在不同光照下的表现。需要注意的是,我们需要观测光照的不同分量的结果,以便于我们模拟光照的具体分量,但实际上这些结果可能是无法直接观测的,所以我们可能会通过一些间接的指标去推断单一分量的影响。
? ? ? ? 漫反射观测? ? ? ??

θh表示了半向量和法线之间的夹角,图表反映了半向量和法线夹角不同时,回射响应的观测结果;其中,左图为光滑材质,右图为粗糙材质
? ? ? ? ?漫反射的表现和材质的粗糙度相关。我可以从上图中观测到材质的回射响应结果,如图,对于光滑的表面,在掠射角处往往具有阴影边缘,而粗糙的表面由于逆向反射在边缘处往往具有小幅度峰值。
? ? ? ? 镜面反射观测
? ? ? ? 镜面反射受到三个分量的影响:
? ? ? ? ① N(法线分布函数),它反映了微平面法线的分布情况。
? ? ? ? 同样的,我们可以从漫反射观测章节中的回测响应来观察到微平面分布函数。我们认为垂直法线入射时产生镜面反射峰值,其中光滑材质的峰值更高,而粗糙材质的峰值较低。随着峰变平,我们认为曲线的其余部分可能是漫反射造成的。
? ? ? ? ② G(几何遮蔽函数),它反映了微平面的光线遮蔽分布情况。

θl表示了法线和灯光方向之间的夹角,图表反映了法线和灯光方向夹角不同时,反照率的变化。反照率是指总反射能量和入射能量之比。其中,左图对应光滑材质,右图对应粗糙材质。
? ? ? ? 我们难以直接测量遮蔽的结果,但是我们可以通过反照率(Albedo)的结果来看出几何遮蔽对光照结果的影响。
????????由上图可见,大部分材质的反照率的值相当低。材质在法线和灯光夹角小于70度的时候,反照率结果相对平坦。在掠射角处,对于光滑的材质,反照率会略微上升再下降;而对于粗糙的材质,反照率会显著增加。
? ? ? ? ③ F(菲涅尔函数),反映了反射的光线所占的比例。

θd表示了半向量和灯光方向(或者半向量和视线)之间的夹角,图表反映了不同材质在半向量和灯光方向夹角不同时,镜面反射所占的比例。虚线代表菲涅尔的理论响应结果,其它实线代表不同材质的实测结果
? ? ? ? ?由图可见,随着光线和视线的夹角变大,反射的比例倾向于增加。对于光滑的表面在掠射角时镜面反射的比例接近1,而对于粗糙的表面,反射率较高但不会完全达到1。
? ? ? ? 部分材质在夹角较大时没有出现镜面反射的峰值,这是由于微表面的遮蔽效应导致的,对视线的遮蔽降低了掠射角的反射率。
?Disney BRDF
????????有了对材质不同光照分量的观测结果后,我们可以尝试使用公式来拟合不同分量。
? ? ? 概念引入
? ? ? ? ?我们先来考虑PBR的一个简单的微平面BRDF模型。它仅考虑了从介质表面当前位置反射的光,因此它可能存在一定的能量损失。??
? ? ? ? 由Disney在2012年的paper中提出:

?? ? ? ? BRDF模拟从介质表面反射的光,这包括了直接的单次反射(镜面反射,specular),以及当前位置附近的多次反射(漫反射,diffuse)。

BRDF模拟了表面的漫反射和镜面反射
? ? ? ? 我们通常将漫反射和镜面反射部分拆开单独计算:?
????????f = Kd * f(diffuse) + Ks * f(specular);
? ? ? ? 其中,Kd为漫反射的比例,Ks为镜面反射的比例,Kd + Ks = 1。
? ? ? ? 一般情况下,我们认为金属主要发生镜面反射,而电介质主要发生漫反射,因此我们在参数化的时候使用“金属度”这样更直观的词汇来概括表面的性质,通常来说,这是一个接近于1或0的值。
? ? ? ? BRDF的参数化?
? ? ? ? BRDF能够表述尽可能多的材质,为了体现不同材质的特性,我们需要使用不同的参数来描述,参考Disney 2012发表的paper的描述,这些参数应该是美术友好的,因此应该遵循如下原则:
????????① 应使用直观而非物理参数
????????② 参数尽量少
????????③ 参数应在其合理范围内为0到1
????????④ 应该允许将参数推到超出其合理范围的合理范围
????????⑤ 参数的所有组合应该尽可能稳健和合理
? ? ? ? 依据这样的准则,Disney设定了如下参数:
? ? ? ? ● BaseColor : 表面颜色,通常用纹理贴图提供;
????????● Subsurface:次表面近似控制漫反射的形状;
????????● Metallic:金属性(0 = 电介质, 1 = 金属)。这是两个不同模型之间的线性混合,它控制了漫反射和镜面反射的比例。金属本身是没有漫反射的,我们指定了镜面反射颜色来控制,等同于BaseColor。
? ? ? ? ● Specular:入射的镜面反射量。这代替了显式的折射率;
????????● SpecularTint:镜面反射的颜色。是一种艺术控制的让步,不同金属有自己对应的颜色值;
????????● Roughness:表面粗糙度,反映了微平面的微观结构。同时控制了漫反射和镜面反射响应;
????????● Anisotropc:各向异性的程度。这控制了镜面高光的纵横比(0 = 各向同性, 1 = 最大各向异性)
????????● Sheen : 光泽度,额外的掠射分量。主要弥补由于仅模拟单次散射造成的能量损失,比如用于衣服材质;
????????● SheenTint : 光泽度的颜色;
????????● Clearcoat:第二个特殊用途的镜面反射项;
? ? ? ? ● ClearcoatGloss : 控制镜面反射波瓣的光泽度(0 = 缎面外观,1 = 光泽外观)

不同参数对材质表面效果的影响
????????Specular BRDF
? ? ? ? Disney使用的镜面反射模型为Cook-Torrance模型,镜面反射部分包括法线分布(D)、几何遮蔽(G)和菲涅尔(F)项, 其计算公式如下:
????????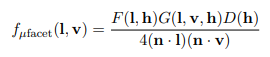 ? ?
? ?
? ? ? ? 法线分布(Normal Distribution)描述了表面方向和中间向量一致性,它反映了表面的平整程度,是描述微表面整体形态的主要参数,它提供了表面镜面高光的形状。
????????此外,为了更好地描述微平面的性质,除了微平面的法线分布,我们还需要考虑到微平面凸起部分对光线遮蔽带来的影响,我们引入了几何遮蔽(Geometric Attenuation or Shadowing Factor)项,它描述了自阴影可见性。由于微平面理论忽略了多次反射,我们认为一旦被遮蔽光线就将消失。
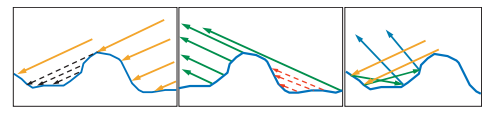
图中反映了微平面的几何遮蔽效应。左图中表现了光线被遮挡,黑色箭头为被遮挡的部分;中间的图表现了视线被遮挡,红色箭头为被遮挡的部分;右图显示了微尺度结构之间正常情况下光的互相反射。
????????最后,还需要考虑到在金属或电介质,不同的观察方向下反射和折射的比例有所差异,通常来说,垂直法线方向观察的时候反射比例最高。我们使用菲涅尔方程(Fresnel)来描述光线反射所占的比例。
? ? ? ? 特别的是,Cook-Torrance给定了一个显式的1/(4 cos θl cos θv)因子,这是由微平面理论推导出来的校正因子,它解释了在微观几何的局部空间和整个宏观表面的空间之间转换的量。
????????Normal Distribution?Function
? ? ? ? 法线分布函数(Normal Distribution?Function)用于描述微表面法线的分布情况,我们将输入粗糙度、法线、中间向量,并得到当前方向上的微表面法线分布与中间向量一致的概率。
? ? ? ? 对于较为光滑的表面,只对于较少方向的输入,NDF能够输出比较大的数值,也就是说与微表面法线和中间向量接近一致的微平面是比较集中的,体现在渲染结果上就会得到集中的明亮的光斑。反之,我们会得到较为灰暗但分布范围较广的结果。微表面法线与中间向量取值一致的概率越大,就越有可能得到较高的光照强度。?
? ? ? ? 微观法线和宏观法线
? ? ? ? NDF是微观几何表面区域上微平面表面法线的统计分布。将NDF沿着微平面法线积分,可以得到微表面的面积。将NDF投影到宏观平面上,可以得到一个归一化的量:
? ? ? ??![]()
???????微观几何法线分布的有符号投影面积之和,应等于宏观表面的有符号投影面积,这必须适用于任何观察方向。在数学上,这意味着对于任何v,函数必须满足这个方程:
????????![]()
? ? ? ? 该方程建立起了宏观法线和微观法线之间的关系。?
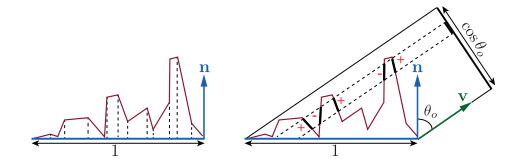
在左侧,为D(m)(n · m),投影到宏观表面平面上的微平面区域积分,可得宏观表面面积(1)。右侧为积分D(m)(v · m),投影到垂直于v平面上的微平面区域,产生宏观表面到该平面的投影,即cos θo 或 (v · n)。多个微平面投影重叠时,背面微平面的负投影区抵消了正面微平面。
?

可见微平面的投影面积之和等于宏观的投影面积
? ? ? ? NDF的外观
? ? ? ? 法线分布函数对整个BRDF外观的贡献是最大的,它的计算方式能够很大程度上影响表面高光的形状,产生不同的“拖影”外观。

? ? ? ? ?上图中左图为传统的Phong模型,右图为PBR模型,两张图中分别演示了Phong和BRDF模型在平面和球体上的高光表现。其中,Phong模型的高光形状沿着反射向量旋转对称,这是错误的;而BRDF的高光形状由于表面的曲率,在平面上呈现为一个长长的拖尾,这与实测的数据更加接近。
? ? ? ? 常用的NDF模型
? ? ? ? 流行的NDF模型包括了GGX, Beckmann,Blinn-Phong。它们的表现如下图所示。

左图表中,不同颜色对应了不同的模型,GGX(红色),Beckmann(绿色),Blinn-Phong(蓝色虚线),曲线反映了镜面峰值的分布,黑色的chrome为实验的对照组
????????其中,Beckmann是较早提出的NDF模型,它在中心模拟了高光的亮点;GGX相比起Beckmann,具有更窄的峰值和更长的拖尾,看起来会更加模糊,这更加匹配实验的数据。
? ? ? ? 但是,无论是Beckmann,GGX还是Blinn-Phong,它们的形状都是不变的。为了能够更好地控制高光的形状,Burley提出了广义Trowbridge-Reitz(GTR) NDF:
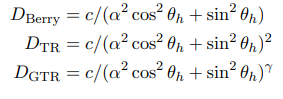
????????在每个分布中,c是比例常数,α是粗糙度参数,其值介于0和1之间;初步拟合结果表明γ的典型值介于1和2之间。
? ? ? ? Disney选择了使用两个固定的镜面反射波瓣,均使用了GTR模型。第一个是基础材质,使用γ = 2,它可以是各向异性的或金属的;第二个是材质上的透明涂层(即Clearcoat),使用γ = 1,它始终是各向同性且为非金属的,它作为一个附加的能量叠加到材质计算结果中。
? ? ? ? 另一方面,Disney使用了α = roughness^2的映射,使得粗糙度在感知上更呈线性变化,这也被广泛用于各个领域。
? ? ? ? NDF计算:GGX分布
? ? ? ? 实时渲染领域比较常用的法线分布函数是GGX分布,以下是GGX分布的各向同性分布版本,其中,n为表面法线,h为中间向量,α为表面粗糙度的重映射(α = roughness ^ 2):

? ? ? ? 对于各向同性材质,我们仅需考虑法线,而对于各向异性材质,由于不同方向光照存在差异,因此我们还需要考虑法线、切线和次切线方向的信息。
? ? ? ? 以下是GGX分布的各向异性分布版本,其中t,b是切线和次切线,αx和αy是对应方向上的粗糙度,它可由各向同性的公式推导而来:
????????
????????αx和αy的差异导致了不同程度的各向异性,我们可以使用单一参数来概括各向异性的程度:


顶行的为Beckmann和底行的GGX。在这两行中,αy?保持不变,αx?从左向右增加
? ? ? ? 以下为各向同性和各向异性GGX的计算:?
// code reference : ue4
// GGX / Trowbridge-Reitz
// [Walter et al. 2007, "Microfacet models for refraction through rough surfaces"]
float D_GGX( float a2, float NoH )
{
float d = ( NoH * a2 - NoH ) * NoH + 1; // 2 mad
return a2 / ( PI*d*d ); // 4 mul, 1 rcp
}
// Anisotropic GGX
// [Burley 2012, "Physically-Based Shading at Disney"]
float D_GGXaniso( float ax, float ay, float NoH, float XoH, float YoH )
{
// The two formulations are mathematically equivalent
float a2 = ax * ay;
float3 V = float3(ay * XoH, ax * YoH, a2 * NoH);
float S = dot(V, V);
return (1.0f / PI) * a2 * Square(a2 / S);
}?????????Geometry计算
? ? ? ? ?几何函数描述了微表面内部遮挡带来的自阴影属性。同样的,它从统计学上返回微表面之间不被相互遮挡的概率。
? ? ? ? ?几何函数返回0意味着完全被遮挡,返回1意味着完全没有自阴影。
? ? ? ? ?我们通常使用Smith方法(G2)描述表面的几何属性,它既考虑到了光线方向的遮挡,又考虑到了观察方向的遮挡,但没有考虑到微平面之间的相互反射,因此会导致最终的结果偏暗。
? ? ? ? Smith方法的最简单的分离存储形式如下:
? ? ? ??![]()
?? ? ??G1对应了单一方向上对光线的遮蔽,这相当于假设光线方向的遮蔽和观察方向的遮挡是不相关的。
? ? ? ? 其中:
![]()
??? ? ? ?Λ函数和对应的NDF相关,也就是说,不同的NDF对应着自己的Smith G1函数。
? ? ? ? 对于各向异性的GGX而言:

? ? ? ? 各向同性的GGX可见性项的计算如下:?
// code reference : ue4
// Smith term for GGX
// [Smith 1967, "Geometrical shadowing of a random rough surface"]
float Vis_Smith( float a2, float NoV, float NoL )
{
float Vis_SmithV = NoV + sqrt( NoV * (NoV - NoV * a2) + a2 );
float Vis_SmithL = NoL + sqrt( NoL * (NoL - NoL * a2) + a2 );
return rcp( Vis_SmithV * Vis_SmithL );
}? ? ? ? ?在实际计算中,我们通常使用SmithJoint近似项模拟GGX的遮蔽项。
?????????Fresnel计算
? ? ? ? 菲涅尔方程反映了光线投射到物体表面后反射和折射的比例。
? ? ? ? 菲涅尔效应和当前的观察视角有一定关联,视线与表面法线越接近90度,反射越明显;反之,视线越平行于法线,折射越明显。
? ? ? ? 此外,物体本身的属性也会影响反射和折射的比例。我们通常使用IOR(Indices of Refraction,折射指数)来定义物体折射的属性。
? ? ? ? 菲涅尔的原始公式非常复杂,在实际运算中,我们通常使用Fresnel-Schlick近似来表达反射比例:
![]()
? ? ? 其中,h是中间向量,v是视线向量,F0是物体的基础反射率。它可以和IOR进行相互转换。
// code reference : ue4
// [Schlick 1994, "An Inexpensive BRDF Model for Physically-Based Rendering"]
float3 F_Schlick( float3 SpecularColor, float VoH )
{
float Fc = Pow5( 1 - VoH ); // 1 sub, 3 mul
//return Fc + (1 - Fc) * SpecularColor; // 1 add, 3 mad
// Anything less than 2% is physically impossible and is instead considered to be shadowing
return saturate( 50.0 * SpecularColor.g ) * Fc + (1 - Fc) * SpecularColor;
}? ? ? 对于电介质而言,两者的转换计算如下:
// code reference : ue4
float DielectricF0ToIor(float F0)
{
return 2.0f / (1.0f - sqrt(F0)) - 1.0f;
}
float DielectricIorToF0(float Ior)
{
const float F0Sqrt = (Ior-1)/(Ior+1);
const float F0 = F0Sqrt*F0Sqrt;
return F0;
}? ? ? ?在实际的计算中,我们还需要一个通解。也就是仅根据PBR的输入参数,如高光项、金属度等得到对应的基础反射率,而无需考虑物体的IOR。我们认为电介质和导体在反射上有着很大的差异,对于导体(金属)而言,通常会得到一个带颜色的反射结果,我们可以直接返回物体本身的颜色。对于大多数电介质而言,我们可以使用0.08 * Specular来概括它的基础反射率。而对于两者之间的金属度取值,我们在这两者之间进行lerp计算。
// code reference : ue4
float DielectricSpecularToF0(float Specular)
{
return 0.08f * Specular;
}
float3 ComputeF0(float Specular, float3 BaseColor, float Metallic)
{
return lerp(DielectricSpecularToF0(Specular).xxx, BaseColor, Metallic.xxx);
}
? ? ? ?Diffuse BRDF
? ? ? ? 漫反射主要发生在电介质上,包括被折射到浅表面后散射、部分吸收和重新发射的光。光线被吸收后,漫反射响应将被表面颜色着色,不同的颜色取决于材质属性,也就是我们参数中所提的BaseColor。
? ? ? ? 常见漫反射模型
? ? ? ? 比较常见的漫反射模型包括Lambert,Oren-Nayar和Hanrahan-Krueger:

三种不同的漫反射表现
?? ? ? ? Lambert 是最为简单的环境光,它假设折射光已经完全散射,失去了方向性,因此漫反射结果在所有方向上均匀分布:
????????
? ? ? ? 对于Lambert材质来说,它的自阴影过暗,掠射角部分非常平坦。在现实中很少有材质表现出Lambert的观测结果。
????????Oren-Nayar是粗糙表面的漫反射表面模型,它忽略了次表面散射和菲涅尔现象,但相比起Lambert,能在掠角处表现出比较强的阴影。
? ? ? ?Hanrahan-Krueger源自次表面散射模型(也称Burley Diffuse),它假设表面非常光滑,不考虑内部体积,模拟了薄物体的透光效果。和Oren-Nayar相反,它在掠射角处偏亮。
? ? ? ? Disney Diffuse
????????接下来我们来看Disney给出的漫反射表达式。
? ? ? ? 我们在前面提到,漫反射模拟了多次反射,光线进入介质内部又出射。因此如果我们考虑到菲涅尔反射,我们至少要考虑光线的两次折射过程:
????????
? ? ? ? 单纯使用Lambert会导致边缘变暗,再考虑菲涅尔效应则会让其更暗。
? ? ? ? 因此,Disney开发了一种新的漫反射经验模型,该模型在平滑表面的漫反射菲涅尔着色和粗糙表面的高光之间过渡。
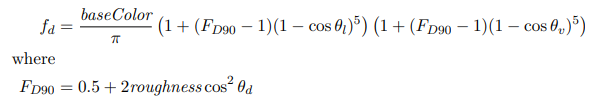
? ? ? ? ?可以看到,它忽略了菲涅尔的折射率,将Schilick公式修改为和表面粗糙度相关的公式,避免传统的菲涅尔效应导致表面过暗的问题。
????????Sheen
? ? ? ?在大部分材质模拟中,出于性能考虑,我们往往只模拟单次散射,而忽略多次散射的计算,这会带来一定的能量损失。为了模拟这种能量的损失,我们引入了sheen(光泽度)项。

如图,添加光泽度项后弥补了粗糙玻璃球损失的能量
?
? ? ? ?一些粗糙的表面如布料等表面的逆向反射(retro-reflection)就可以用光泽度来模拟,它往往是一个非白色的结果。比如头发的高光往往有两层,其中一层有色的就是由多次散射贡献的。
? ? ? ? 光泽度的色调可以从基础颜色的饱和度中提取:
// code reference : https://schuttejoe.github.io/post/disneybsdf/
static float3 CalculcateTint(float3 baseColor)
{
// the color tint is never mentioned in the SIGGRAPH presentations as far as I recall but it was done in the BRDF exporler so I'll replicate that here
float luminance = dot(float(0.3f, 0.6f, 1.0f), baseColor);
return (luminance > 0.0f) ? baseColor : (1.0f/luminance) : float3::One_;
}? ? ? ? 最终光泽度的计算还需要考虑到菲涅尔:
// code reference : https://schuttejoe.github.io/post/disneybsdf/
static float3 EvaluateSheen(const SurfaceParameters& surface, const float3& wo, const float3& wm, const float3& wi)
{
if(surface.sheen <= 0.0f) return float3::Zero;
float dotHL = dot(wm, wi);
float3 tint = CalculateTint(surface.baseColor);
return surface.sheen * lerp(float3(1.0f), tint, surface.sheenTint) * Fresnel::SchlickWeight(dotHL);
}????????ClearCoat
????????用来模拟材质表面的透明涂层,它作为一个额外添加的项,模拟了更加完整的BRDF。
????????它的基本公式和BRDF一致,包含了法线分布(D)、几何衰减(G)和菲涅尔(F)项。
????????其中,几何衰减项使用了固定的0.25的粗糙度:
????????
????????菲涅尔项使用了1.5的IOR(即f0 = 0.04)。
Disney BSDF
? ? ? ? Disney BRDF实际上是一个电介质和金属模型的混合,为了扩展支持光线的折射分量,我们添加了一个额外的镜面反射BSDF和内部的体积着色来进行扩展,再结合集成的次表面散射,得到了我们统一的BSDF模型,这样就能够概括绝大多数的材质模型。
? ? ? ? 由于包含了次表面散射模型,更严谨的我们把该统一模型称为集成次表面散射的Disney BSDF。
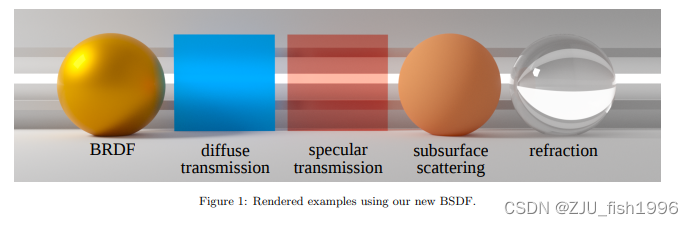
由图可见,除了BRDF支持的金属和电介质,统一的BSDF模型还支持了薄透射表面、次表面表面和透明折射表面。
????????BSDF的组成
? ? ? ? 统一的BSDF模型由Disney在2015年提出:

????????如图,我们考虑光线从物体表面反射和折射的部分。其中,使用metallic参数描述物体的金属度,并用于混合金属和电介质两种模型,使用specular transmission参数描述物体的透射率,并使用透射率在镜面BSDF和电介质BRDF进行混合。
? ? ? ? BSDF的参数化?
? ? ? ? 在BSDF的基本模型中,Disney添加了如下参数:
? ? ? ? ● SpecTrans:光线的Specular透射率。折射进入物体的光线有多少比例发生镜面透射;
? ? ? ? ● Flatness:平坦度。应用于薄表面,反映了次表面散射所占的比例,替代了原先的subsurface参数;
? ? ? ? ● DiffTrans:光线的Diffuse透射率。应用于薄表面,反映了薄表面漫反射和漫透射的比例;
? ? ? ? ● IOR:Index of Refraction,折射率,折射光线的角度,会影响背面景象的扭曲度,该参数的结果接近于线性,合理范围是[1,2],常见材质接近1.5;
? ? ? ? ● Clearcoat:清漆层;和BRDF保持一致,提供额外的反射且不参与折射;
? ? ? ? ● Surface absorption:表面吸收颜色,其中薄表面考虑进入和退出的散射事件,将折射结果乘以表面颜色平方根;
? ? ? ? ● Volumetric absorption:体积吸收颜色,根据穿过固体的折射路径长度来应用体积吸收;根据Beer-Lambert定律,体积透射率(T) 和光学深度(d)成指数关系,吸收吸收(σa) = -(log T)/d。但是吸收系数参数并不直观,因此我们指定特定距离后会达到某个透射颜色;
? ? ? ? ● Sheen:光泽度,非物理的参数,用于补偿未统计微表面相互反射/折射带来的能量损失;
? ? ? ? ● ScatrDist:散射距离;用于次表面散射的模拟,描述次表面散射的最远距离;
? ? ? ? Diffuse?BSDF
? ? ? ? Disney扩展了电介质BRDF模型,使其可以和次表面散射集成,重构漫反射的定义为:

? ? ? ? 我们保留了粗糙表面的菲涅尔因子和逆向反射项,并且f(lambert)项可交换为次表面散射项。
? ? ? ? 结合Disney Diffuse BSDF和Thin BSDF,在Diffuse BSDF计算公式中,f(lambert)要么是一个简单的lambert项;或者,我们还可以计算薄表面,它会基于flatness参数在lambert和hanrahan krueger diffuse模型之间进行混合,得到完整的Diffuse计算代码:
// code reference : https://schuttejoe.github.io/post/disneybsdf/
static float EvaluateDisneyDiffuse(const SurfaceParameters& surface, const float3& wo, const float3& wm,
const float3& wi, bool thin)
{
float dotNL = AbsCosTheta(wi);
float dotNV = AbsCosTheta(wo);
float fl = Fresnel::SchlickWeight(dotNL);
float fv = Fresnel::SchlickWeight(dotNV);
float hanrahanKrueger = 0.0f;
if(thin && surface.flatness > 0.0f) {
float roughness = surface.roughness * surface.roughness;
float dotHL = Dot(wm, wi);
float fss90 = dotHL * dotHL * roughness;
float fss = Lerp(1.0f, fss90, fl) * Lerp(1.0f, fss90, fv);
float ss = 1.25f * (fss * (1.0f / (dotNL + dotNV) - 0.5f) + 0.5f);
hanrahanKrueger = ss;
}
float lambert = 1.0f;
float retro = EvaluateDisneyRetroDiffuse(surface, wo, wm, wi);
float subsurfaceApprox = Lerp(lambert, hanrahanKrueger, thin ? surface.flatness : 0.0f);
return InvPi_ * (retro + subsurfaceApprox * (1.0f - 0.5f * fl) * (1.0f - 0.5f * fv));
}? ? ? ? ?可见,subsurfaceApprox项根据flatness参数在lambert和hanranhanKrueger中过度。整个漫反射公式考虑了逆向反射,漫反射和漫透射,并考虑了菲涅尔的影响。
????????Specular BSDF

????????我们把折射光线在介质边界内的镜面传输使用Specular BSDF建模。
????????镜面BSDF直接将镜面BRDF反射扩展到了折射,它的绝大部分计算和BRDF保持一致,包括相同的几何项和分布项,差异主要体现在菲涅尔项由F变为1-F,且引入了IOR校正。
????????由于镜面BSDF描述了折射的部分,因此我们需要考虑介质的折射率,光线的折射遵循Snell定律,满足ηi sin θi = ηo sin θo。其中ηi 和 ηo是折射表面上两种介质的折射率。通常我们仅考虑相对IOR,即η = ηo/ηi。我们通常认为空气的IOR近似于1,此时折射率等同于相对折射率。
? ? ? ?在计算反射的时候,我们使用了Schlick Fresnel近似,这对于BRDF是可行的。但对于折射而言需要更加小心,因为这可能会产生临界角的问题,或在相对IOR接近于1的时候会产生异常亮度。下图显示了Shlick存在的这两个问题:
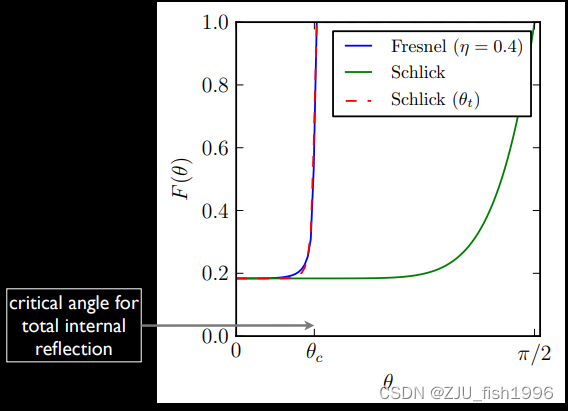
如图,使用 Schlick 进行内部反射时会出现问题,临界角为1,可见绿色曲线在临界角之后产生大幅的偏移。可使用Schlick (θt)而非Schlick (θi)来简单地规避这个问题

当IOR接近1的时候存在问题。如1.02 是水中冰的相对 IOR,
此时Schlick 的亮度高达 40 倍。
?
? ? ? ? 因此镜面BSDF使用了精确的电介质菲涅尔方程,因为折射角θt本身就是需要计算的,额外的开销不算太高:

????????镜面BSDF在改变IOR、specTrans、吸收系数后的渲染效果如下,其中,IOR影响了折射率,因而影响了我们看到的透明物体后的图像的形态,可能会产生弯曲的外观;specTrans影响了镜面BSDF的比例,它影响了透明物体后的图像可视比例;

顶部:IOR从1到2变化(左边的球体显示为1.02而不是1,否则它将不可见)
底部:specTrans从0到1变化,IOR为1.33.
?
? ? ? ? 吸收系数反映了有多少光线被吸收,光线的特定分量被吸收导致了不同的颜色。根据Beer-Lambert定律,吸收系数和距离成指数关系,因此距离越长颜色越浅。
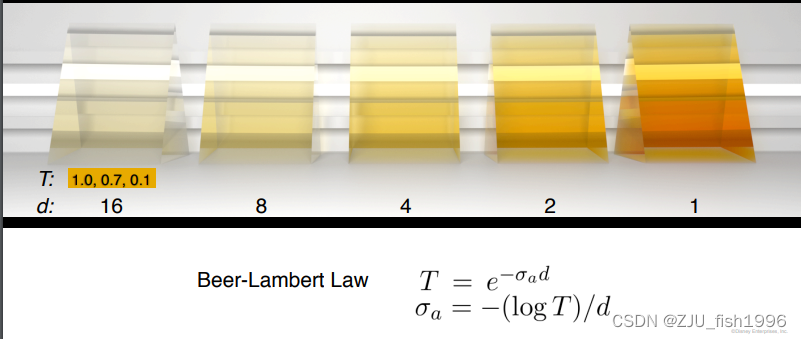
参数化吸收系数是不直观的,我们可以指定透射颜色和达到该颜色的距离,
并可以从中推断出吸收系数。
?
? ? ? ? 特别的,对于薄表面来说,有效透射粗糙度应该取决于IOR,因为折射弯曲可以放大或衰减透射模糊。 通过基于 IOR 缩放粗糙度可以实现更好的匹配。??
? ? ? ? ?以下为Disney BSDF Specular的代码,它特殊处理了薄表面,使用基本颜色的平方来建模进入进出事件,并根据IOR重映射了表面的粗糙度:
// code reference : https://schuttejoe.github.io/post/disneybsdf/
//===================================================================================================================
static float ThinTransmissionRoughness(float ior, float roughness)
{
// -- Disney scales by (.65 * eta - .35) based on figure 15 of the 2015 PBR course notes. Based on their figure
// -- the results match a geometrically thin solid fairly well.
return Saturate((0.65f * ior - 0.35f) * roughness);
}
//===================================================================================================================
static float3 EvaluateDisneySpecTransmission(const SurfaceParameters& surface, const float3& wo, const float3& wm,
const float3& wi, float ax, float ay, bool thin)
{
float relativeIor = surface.relativeIOR;
float n2 = relativeIor * relativeIor;
float absDotNL = AbsCosTheta(wi);
float absDotNV = AbsCosTheta(wo);
float dotHL = Dot(wm, wi);
float dotHV = Dot(wm, wo);
float absDotHL = Absf(dotHL);
float absDotHV = Absf(dotHV);
float d = Bsdf::GgxAnisotropicD(wm, ax, ay);
float gl = Bsdf::SeparableSmithGGXG1(wi, wm, ax, ay);
float gv = Bsdf::SeparableSmithGGXG1(wo, wm, ax, ay);
float f = Fresnel::Dielectric(dotHV, 1.0f, 1.0f / surface.relativeIOR);
float3 color;
if(thin)
color = Sqrt(surface.baseColor);
else
color = surface.baseColor;
// Note that we are intentionally leaving out the 1/n2 spreading factor since for VCM we will be evaluating
// particles with this. That means we'll need to model the air-[other medium] transmission if we ever place
// the camera inside a non-air medium.
float c = (absDotHL * absDotHV) / (absDotNL * absDotNV);
float t = (n2 / Square(dotHL + relativeIor * dotHV));
return color * c * t * (1.0f - f) * gl * gv * d;
}? ? ? ? Thin BSDF
? ? ? ? 在Disney BSDF中,特殊的考虑了薄表面。包括我们前文在Diffuse BSDF和Specular BSDF中,都处理了薄表面的情况。

????????对于薄表面的Diffuse项而言,相比起实体,我们保留了BRDF的次表面近似公式(即hanranhanKrueger)来替代漫反射形状,并使用flatness参数来描述次表面散射的比例。我们不再使用subsurface参数是为了避免和真正的次表面散射混淆,由于这只是一个次表面散射的近似公式。
? ? ? ? 此外,薄表面包含了漫透射的系数:

对于薄表面,漫反射和漫透射的不同比例的光照分布如上图所示
特别的是,漫反射的背面散射是不包含菲涅尔项的,多次散射失去了方向性
?
? ? ? ? 对于薄表面的Specular项而言,相比起实体,薄表面上的折射引起的弯曲几乎可以抵消,因此我们使用与我们的BRDF镜面波瓣等效的微平面分布来模拟镜面透射率。然而,这并不完全令人满意,因为有效透射粗糙度应该取决于IOR,因为折射弯曲可以放大或衰减透射模糊。通过基于 IOR 缩放粗糙度(仅用于传输)可以实现更好的匹配。

左图:IOR呈条带变化的几何实体,每个条带的粗糙度为0.35,透射模糊随着IOR的增加而明显增加。右图:透射粗糙度按(0.65η - 0.35) 缩放以近似匹配的薄表面 BSDF 近似。
?
???????BSSRDF
? ? ? BSSRDF全称Bidirectional Scattering Surface Reflectance Distributed Function(双向散射表面反射率分布函数)。它描述了次表面散射光线和入射光线的比例。
????????次表面散射意味着出射位置和入射位置有可能不一致,因此对于特定的观察方向,它的光源可能来自任意入射方向。
????????为了模拟真实的次表面散射效应,我们可以使用随机路径跟踪计算次表面散射,但这是非常耗时的:
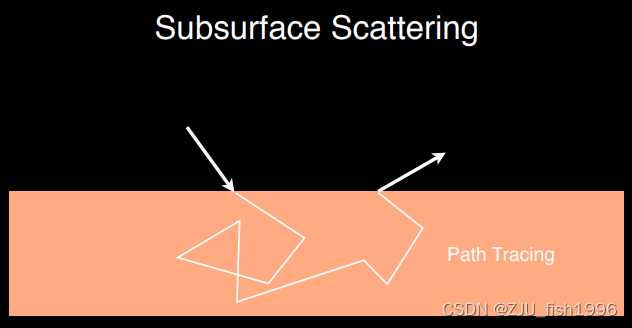
使用路径追踪模拟次表面散射
? ? ? ? ?我们引入了预计算的漫反射曲线,并选取随机距离(下图中的r),通过曲线查找到该点的能量,我们称之为扩散函数(Diffusion):
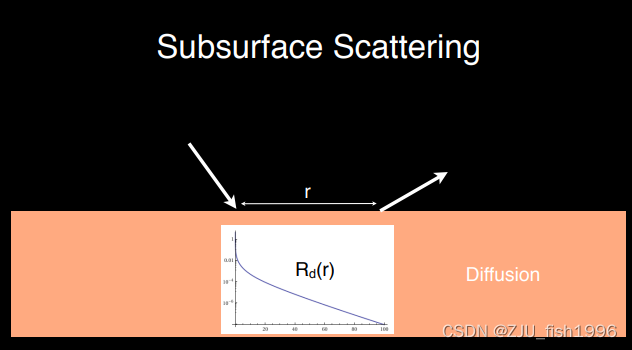
使用漫反射分布曲线模拟次表面散射
?
? ? ? ? ?通过拟合近似得到的归一化的Diffusion函数如下:

其中r对应于所选两点之间(入射和出射)的距离,d代表次表面散射的分布距离
????????我们可以对距离进行积分计算来累加不同位置的贡献度,得到最终的次表面散射颜色。

不同scatterDist对应的拟合结果
?
? ? ? ? 整体的模拟过程可以概述为:
????????① 计算每个像素的漫反射颜色
????????dot(N,L) * diffuseColor,并进行模糊处理,计算时剔除无效的背面像素。
????????② 预计算权重查找表
? ? ? ? diffusion只考虑了入射点和出射点的距离,相当于假设在一个无限的平面上进行积分,但实际上我们还应该考虑灯光方向和表面的弯曲程度(即曲率)。
? ? ? ? 因此,基于Disney的Diffusion,在实际的应用通常还会预计算一张二维查找表,查找坐标为dot(N,L)和曲率(1/r = ΔN/Δp)
????????一般而言,曲率越大,次表面散射越明显。
????????③ 根据贡献权重加权周围每个像素对当前像素的贡献
????????卷积范围由当前像素深度及其导数决定,由于分布不完全均匀,采样时使用重要性采样。
? ? ? ? 以下为Path Tracing和Diffusion计算结果的对比:

左图:使用次表面扩散渲染的图像,小水滴明显太暗,褶皱复杂的区域太亮,显得发光;
右图:路径追踪的次表面散射模拟可避免这些瑕疵。
?
环境光照
? ? ? ? 迄今为止,我们讨论的一直是直接光照与材质的交互。实际上,场景中的物体除了会受到直接光照外,还会收到从其它物体多次反弹而来的间接光照。我们可以将其概述为环境光照。
? ? ? ? IBL
? ? ? ? 哪怕对于同一个材质,在不同的环境下,比如在晴朗的平原,或者茂密的森林,又或者是昏暗的密室,它的表现也是不一样的。对于镜面反射的部分,还可以看到周围物体的反射结果。
? ? ? ? 为了使得物体和环境更好地融合起来,我们可以通过光线追踪来计算来自环境的光照,但是,这样的计算是比较耗时的。
????????为了达到实时的高性能,我们提供了一张立方体环境贴图作为近似的环境光源,其中贴图的每个像素都被视为一个光源。这个过程称为IBL,IBL也就是基于图像的光照(Image Based Lighting)。
? ? ? 对于IBL而言,对于较大的场景,仅使用一张贴图是不足的,因此往往会基于光照探针进行,也就是说当前位置使用哪张环境贴图,取决于离它最近的光照探针。
????????模拟环境光源意味着入射方向可以是无穷多的,这意味着我们需要对入射方向进行积分计算。由于实时计算积分效率较低,因此往往采用预计算的方式实现,我们最终的代码包含了预计算和实时计算两部分。
? ? ? ? 接下来我们讨论ue4引擎早期发布的paper中给出的一套IBL算法,它在求解IBL时,我们会把公式分为两个部分:漫反射+镜面反射。
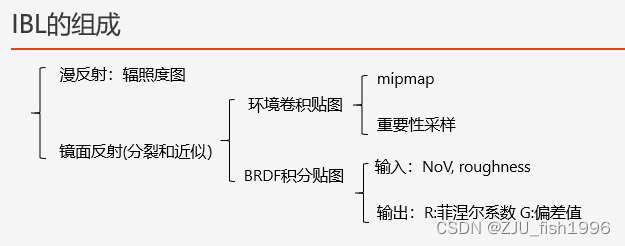
?? ? ? ?漫反射部分
????????其中漫反射仅受入射方向影响,因此仅需在半球区域内针对每个特定的出射方向,对不同入射方向进行离散采样并累加求均值即可。每个出射方向计算得到一个对应的结果,存储在辐照度图(立方体贴图)中。
? ? ? ? 镜面反射部分
????????镜面反射同时受到入射和出射方向的影响,也就是说它是一个双重积分,存储复杂度较高。这里具体的含义是:我们需要输入入射和出射方向来查找对应的结果,两者所有可能的组合数据量是非常大的。
? ? ? 我们可以参考ue4的做法,将其近似拆分为两部分,称为分裂和近似(Split Sum Approximation),可以将其简化为两个积分的乘积。预计算的信息存储在两张不同的贴图上,在最终着色计算的时候组合起来。
????????
? ? ? 镜面反射的第一部分是预计算的环境贴图。它和漫反射的辐照度图类似,不同之处主要有两点:
? ? ? ① 漫反射的分布较为均匀,而镜面反射分布较为集中,因此采样时使用重要性采样。采样向量借助NDF构造,并假设视角方向等于镜面反射方向,也就是分布的形状不会随着观察方向的改变而改变,即N = V = R。
? ? ? ② 由于粗糙度越大,镜面反射越模糊,因此可以使用mipmap来维护不同粗糙度的卷积信息。
? ? ? ? 以下为第一部分的实时部分的计算。
// code reference : ue4
float Mip = ComputeReflectionCaptureMipFromRoughness(Roughness, View.ReflectionCubemapMaxMip);
float4 Sample = TextureCubeArraySampleLevel(ReflectionStruct.ReflectionCubemap,
ReflectionStruct.ReflectionCubemapSampler,
ProjectedCaptureVector, SingleCaptureArrayIndex, Mip);? ? ? ?镜面反射的第二部分是BRDF的卷积,我们将结果存储为LUT查找表,输入坐标是dot(N, V) 和 roughness,输出信息是菲涅尔系数和偏差值。
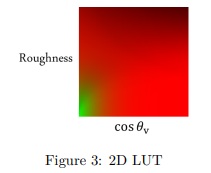
?
????????同样的采样时使用重要性采样,结果根据几何项和菲涅尔项进行计算。
? ? ? ? 以下为第二部分的实时部分的计算:
// code reference : ue4
half3 EnvBRDF( half3 SpecularColor, half Roughness, half NoV )
{
// Importance sampled preintegrated G * F
float2 AB = Texture2DSampleLevel( PreIntegratedGF, PreIntegratedGFSampler, float2( NoV, Roughness ), 0 ).rg;
// Anything less than 2% is physically impossible and is instead considered to be shadowing
float3 GF = SpecularColor * AB.x + saturate( 50.0 * SpecularColor.g ) * AB.y;
return GF;
}? ? ? ? 全局光照
????????除了IBL外,我们在实时渲染中常用的模拟间接光照的技术还包括如下几种:
? ? ? ? ① 屏幕空间的算法。包括SSR(屏幕空间反射)、SSGI(屏幕空间全局照明)等,它们都是利用光线步进(RayMarch)在屏幕空间进行光线追踪,获取附近的像素点信息。
? ? ? ? 其中SSR会从当前像素点发出一条反射的光线,直到捕获到相交的像素作为反射结果,而实时的SSGI计算方式则是在屏幕空间某个点上,发射多条射线进行RayMarch,在碰撞点采样多个颜色计算平均值,得到最终环境光的颜色值。
? ? ? ? ② 灯光贴图和灯光采样点。
? ? ? 对于静态物体,通常通过烘焙光图来记录环境光数据,而对于静态和动态物体,都可以使用在场景中摆放采样点来收集记录对应位置的环境光数据。这两者使用二阶或三阶的球谐数据来存储光照信息,且都是离线收集的。
? ? ? ? 以上方法模拟了更加真实的全局间接光照,全局光照一个最明显的表现就是渗色(color bleeding),物体之间会相互照亮并影响对方的外观。
? ? ? ? 完整光照环境
? ? ? ? 让我们更综合的来考虑实时渲染中物体受光的影响。
? ? ? ? 在场景中,通常会有一个主光源,它作为平行光存在。此外,还会有一些局部灯光(local light),作为氛围光源存在,包括聚光灯、点光源。其余的作为环境光照存在,作为整体的补光,实现方式包括IBL或lightmap等。
? ? ? ? 完整的光照作用到物体上后,会产生如下效果:
????????光比
? ? ? ?光比是指场景画面亮处和暗处的受光比例。
? ? ? ?较小的光比能够营造比较柔和的效果,而较大光比的明暗反差能带来层次感,但反差过大会导致丢失亮部/暗部的细节,产生过曝/欠曝的现象。

? ? ? ? 灯光的强度越强,就会显得阴影部分越深。通常场景中会使用一盏太阳光作为主光,通过补充光源能够调节光比,比如添加环境光后,可以降低光比。
?????????明暗交界
????????明暗交界线是指物体亮面和暗面的交界部分。
? ? ? ?硬光会产生比较清晰的交界线,而柔光的交界线更加模糊。一般来说,较远的太阳光更接近硬光,而近处的聚光灯能够产生柔光。

? ? ? ? 亮处和暗处的比例决定了画面的整体明暗平衡,即大部分颜色分布在亮色还是暗色。接近1:1的明暗比例会导致逆光环境下颜色基本分布在暗色中,失去体积感。
? ? ? ?在材质中,我们通常使用dot(N,L)来表现每处的受光比例,其中,N代表物体表面的法线,L代表灯光方向。通过dot(N,L)的映射计算,我们可以调整画面的明暗平衡,如计算dot(N,L)的平方, ? ? ? ? ? ?我们所熟知的Half Lambert,就是将像素接收光量的计算改为dot(N,L) * 0.5 + 0.5,使得亮面面积增大。
? ? ? ? 更近一步,可以推广出Wrapped Diffuse的算法:saturate((dot(N,L) + w) / (1 + w))。

? ? ? ? 阴影和环境光遮蔽
? ? ? ? 直接光照不到的地方,我们称之为阴影(Shadow);而环境光被遮挡的效应,我们称之为环境光遮蔽(AO)。
? ? ? ? 我们可以认为,直接光照产生的阴影提升了整体画面的层次感,而环境光遮蔽提升了画面暗部的层次感。我们可以通过烘焙的AO贴图或SSAO来模拟环境光遮蔽。
? ? ? ? Bent Normal
? ? ? ? Bent Normal对原有的Normal做修改,指向了光线传入的主要方向,这是考虑了可能存在的自遮挡。
? ? ? ? 我们知道,Normal是通过高模信息生成的,但它没有考虑到来自模型的遮挡。Bent Normal可以用来模拟一些模型信息无法描述的高频细节光照信息,进而解决间接光照漏光的问题。
ue4中的PBR渲染
? ? ? ?ue4基于迪士尼实现了一套比较完整的PBR渲染流程,并进行了一定的简化。它支持的PBR材质包括:默认PBR、次表面散射、预计算皮肤、涂层、双面植被、屏幕空间次表面散射、头发、衣服、水体、薄透明表面等。
? ? ? ? 在代码库中,ue4实际上实现了非常完整的各个不同模型,这些代码都是非常值得参考的:
| Diffuse | Lambert、OrenNayar、Burley、Gotanda |
| D | Blinn、Beckmann、GGX、 |
| G | Neumann、Kelemen、Schlick、Smith、SmithJoint |
| F | Schlick、Fresnel |
????????默认的PBR
? ? ? ? ?默认的PBR材质基于迪士尼BSDF,可用于描述金属模型、大部分不透明物体、薄表面以及
部分次表面模型。其中我们会计算漫反射、高光的贡献,并考虑当前的透射度。
? ? ? ? 镜面反射项中,法线分布使用GGX,遮蔽函数使用近似SmithJoint,菲涅尔使用Schlick近似,漫反射项使用的是Lambert项。各向异性材质并没有特定的着色模型,而是作为一个材质输入参数,方便与各种着色模型进行组合。
?????????次表面散射

?
? ? ? ? 默认的PBR提供了一种比较廉价的次表面散射计算方式,可以用来模拟蜡烛、雪、玉石等一些场景物件,它考虑了物体的透光性,但未使用复杂的积分计算。
? ? ? ?它表现为给物体整体一个次表面颜色的补偿,在物体不受直接光照影响的背面次表面颜色的贡献更大。
? ? ? ?使用Transimission参数来控制3s的强度,Transimission为0时,则会走普通的PBR材质。
? ? ? ? 在背光的情况下我们给出接近1的散射强度,在受光面则给予和当前表面法线和AO相关的整体散射强度。受光面的散射强度在法线与中间向量接近平行的时候较大,透明度越低的时候,整体的散射强度也会更强:
// to get an effect when you see through the material
// hard coded pow constant
float InScatter = pow(saturate(dot(L, -V)), 12) * lerp(3, .1f, Opacity);
// wrap around lighting, /(PI*2) to be energy consistent (hack do get some view dependnt and light dependent effect)
// Opacity of 0 gives no normal dependent lighting, Opacity of 1 gives strong normal contribution
float NormalContribution = saturate(dot(N, H) * Opacity + 1 - Opacity);
float BackScatter = GBuffer.GBufferAO * NormalContribution / (PI * 2);
// lerp to never exceed 1 (energy conserving)
Lighting.Transmission = AreaLight.FalloffColor * ( Falloff * lerp(BackScatter, 1, InScatter) ) * SubsurfaceColor;????????双面透明材质
? ? ? ? 双面透明材质基于默认的PBR材质计算transimission参数,它可用于模拟薄表面。
? ? ? ? 为了模拟光线透过物体表面的效果,我们需要获取物体的背面信息,我们认为法线和光线异向的时候为背面,ue4这里使用了Wrap Lighting算法,对法线和光线的点积做更好的重映射:
float WrapNoL = saturate((-dot(N, L) + Wrap) / square(1 + wrap));? ? ? ? wrap值取0.5,将得到一个近似守恒的更均匀的光线分布结果。
? ? ? ? 此外,我们还需要考虑光线在物体内部散射的程度。我们使用GGX法线分布来计算,其中,由于背光的特殊性质,我们给定0.6的固定粗糙度,并只考虑光线和视线异向时的贡献:
float Wrap = 0.5;
float WrapNoL = saturate( ( -dot(N, L) + Wrap ) / Square( 1 + Wrap ) );
// Scatter distribution
float VoL = dot(V, L);
float Scatter = D_GGX( 0.6*0.6, saturate( -VoL ) );
Lighting.Transmission = AreaLight.FalloffColor * (Falloff * WrapNoL * Scatter) * SubsurfaceColor;????????预积分皮肤(PreintegratedSkin)
? ? ? ? 预积分的皮肤基于默认的PBR材质计算transimission参数,它使用了一张预积分的LUT作为输入,是一种简单高效的皮肤渲染方式。输入的LUT贴图是固定无法修改的。
? ? ? ? 皮肤的2D LUT贴图的两个输入坐标分别是dot(N,L)和皮肤表面的曲率1/r,ue4中使用1-Opacity作为表面的曲率。返回的结果是预计算的BRDF值。
float3 PreintegratedBRDF = Texture2DSampleLevel(View.PreIntegratedBRDF,
View.PreIntegratedBRDFSampler,
float2(saturate(dot(N,L) * .5 + .5),1 - Opacity), 0).rgb;? ? ? ? 大部分的计算都在预处理过程中完成,因此实时计算的部分相对简单。
????????次表面轮廓(Subsurface Profile)

?
? ? ? ? 相比起预积分的皮肤,一种更加真实且昂贵的皮肤渲染方案。
? ? ? ? 皮肤会计算两层高光。
? ? ? ? 其中,第一层和第二层高光的粗糙度以及混合比例我们通过预计算的方式存储下来,并考虑透明度对高光的影响,透明度较高时,粗糙度值取接近1的值:
Lobe0Roughness = lerp(1.0f, Lobe0Roughness, saturate(Opacity * 10.0f));
Lobe1Roughness = lerp(1.0f, Lobe1Roughness, saturate(Opacity * 10.0f));? ? ? ? 两层高光分别计算GGX的法线分布,并乘以对应的粗糙度相关的系数,最终按照预计算的比例进行混合:
float AverageAlpha2 = Pow4(AverageRoughness);
float Lobe0Alpha2 = Pow4(Lobe0Roughness);
float Lobe1Alpha2 = Pow4(Lobe1Roughness);
float Lobe0Energy = EnergyNormalization(Lobe0Alpha2, Context.VoH, AreaLight);
float Lobe1Energy = EnergyNormalizatoin(Lobe1Alpha2, Context.voH, AreaLight);
float D = lerp(D_GGX(Lobe0Alpha2, Context.NoH) * Lobe0Energy,
D_GGX(Lobe1Alpha2, Context.NoH) * Lobe1Energy, LobeMix);? ? ? ? 遮蔽函数和菲涅尔则只需计算一次,使用材质本身提供的输入:
float Vis = Vis_SmithJointApprox(AverageAlpha, Context.NoV, NoL);
float3 F = F_Schlick(SpecularColor, Context.VoH);????????皮肤的漫反射使用了Disney2012年的Burley Diffuse,它更加适用于模拟次表面散射。
????????透明涂层(ClearCoat)
? ? ? ? ?ClearCoat模拟材质表面的透明涂层,比如汽车表面的涂层。
? ? ? ? ?为了表现物体表面的涂层,需要将材质分为两层,即BaseLayer和ClearcoatLayer。两层材质对整体颜色的贡献按对应的权重累加,ClearcoatLayer和BaseLayer的贡献分布由clearcoat参数控制。作为分层材质,整个材质计算较为复杂。
? ? ? ??Clearcoat Layer
? ? ? ? 作为物体表面特殊的材质层存在。
? ? ? ? Specular
? ? ? ?首先我们来考虑specular计算部分。
? ? ? ?对于ClearcoatLayer而言,ue4提供了独立的法线(可选)、粗糙度输入接口来做更精细的控制。和普通PBR一样,它使用GGX的法线分布,近似Smith作为遮蔽函数,使用IOR为1.5的固定参数计算菲涅尔。特别的是,法线分布额外考虑了Clearcoat的能量贡献:
float F0 = 0.04;
float Fc = Pow5(1 - Context.VoH);
float F = Fc + (1 - Fc) * F0;
float ClearCoatEnergy = EnergyNormalization(a2, Context.VoH, AreaLight);
float D = D_GGX(a2, Context.NoH) * ClearCoatEnergy; // a2: clearcoat roughness
float Vis = Vis_SmithJointApprox(a2, Context.NoV, NoL);
float Fr1 = D * Vis * F;
Lighting.Specular = ClearCoat * AreaLight.FalloffColor * (Falloff * NoL * Fr1);? ? ? ? 对于BaseLayer而言,会根据ClearCoat的大小,在默认高光(Default Specular) 和折射高光(Refracted Specular) 之间进行混合,ClearCoat越大,折射高光占比越大。
? ? ? ? 默认高光和常规的Default Lit一样,折射高光在默认高光的基础上,使用了不一样的菲涅尔值:
float3 RefractedF = lerp(0.0, F, GBuffer.Metallic);? ? ? ? 这意味着在非金属表面发生折射时,在顶部和底部介质之间的IOR接近1,使得菲涅尔折射为一个接近0的值。
? ? ? ? 此外,折射高光还考虑了透射率,透射部分需要考虑独立的菲涅尔系数:
float FresnelCoeff = (1.0 - F1) * (1.0 - F2);? ? ? ? 最终的计算如下:
float3 CommonSpecular = (Energy * Falloff * D2 * Vis2) * AreaLight.FalloffColor;
float3 DefaultSpecular = F * NoL;
float3 RefractedSpecular = FresnelCoeff * Transmission * RefractedF * BottomContext.NoL;
Lighting.Specular += CommonSpecular * lerp(DefaultSpecular, RefractedSpecular, ClearCoat);?? ? ? ? Diffuse
? ? ? ? 接下来我们考虑Diffuse部分,我们只需计算BaseLayer部分。
? ? ? ? 和Specular的BaseLayer类似,我们在默认漫反射(Default Specular) 和折射漫反射(Refracted Diffuse) 之间进行混合:
Lighting.Diffuse = lerp(DefaultDiffuse, RefractedDiffuse, clearcoat);? ? ? ? 其中,Default Diffuse使用了Lambert环境光:
float3 DefaultDiffuse = (Falloff * NoL) * AreaLight.FalloffColor
* Diffuse_Lambert(GBuffer.DiffuseColor);? ? ? ? Refracted Diffuse和Specular类似,需要考虑透射和独立的透射菲涅尔。
float3 RefractedDiffuse = FresnelCoeff * Transmission * DefaultDiffuse;????????布料材质
? ? ? ? ue4中布料的Diffuse使用了较为简单的Lambert Diffuse。
? ? ? ? Specular使用了两层高光,根据布料系数在两层高光之间混合:
Lighting.Specular = lerp(Spec1, Spec2, Cloth);? ? ? ? 其中,第一级高光为常规的GGX高光,第二级高光则为Inverse GGX的法线分布,以及针对Cloth的遮蔽函数,菲涅尔使用次表面颜色进行计算:
float D = D_InvGGX(Pow4(GBuffer.Roughness), Context.NoH);
float Vis = Vis_Cloth(Context.NoV, NoL);
float3 F = F_Schlick(FuzzColor, Context.VoH);????????头发材质
? ? ? ? 头发渲染并没有使用Kajiya模型,而使用了更物理的模型,渲染分为三个模块:
? ? ? ? ① R。头发表面的反射部分。呈现光的颜色。
? ? ? ? ② TT。光线折射进入头发后又从另一侧出射的部分。
? ? ? ? ③ TRT。光线折射进入头发后,在内部中散射,最后出射的部分(次表面散射)。带头发颜色。
? ? ? ? R,TT,TRT都包含了F,M,N项,其中,F项对应了菲涅尔项,M项和N项分别对应纵切面和横切面的散射分布项。
? ? ? ? M项
? ? ? ? M项使用正态分布计算散射分布(N项和M项类似):
float Hair_g(float B, float Theta)
{
return exp(-0.5 * Pow2(Theta) / (B * B)) / (sqrt(2 * PI) * B);
}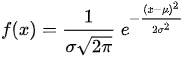
? ? ? ? ?其中,μ代表分布的位置,在头发的渲染中位置无偏移,这里取0。
? ? ? ? ?σ代表分布的幅度即形状,σ和物体的粗糙度相关:
? ? ? ? F项
? ? ? ? ?F项的计算如下,取了固定的折射率:
float Hair_F(float CosTheta)
{
const float n = 1.55;
const float F0 = Pow2((1 - n) / (1 + n));
return F0 + (1 - F0) * Pow5(1 - CosTheta);
}? ? ? ? ?R、TT和RTR
? ? ? ? R部分是菲涅尔和普通镜面反射相乘,Specular越大,反射越强,因为光线没有进入发丝,所以没有头发的BaseColor。
float Np = 0.25 * CosHalfPhi;
float Fp = Hair_F(sqrt(saturate(0.5 + 0.5 * VoL)));
S += Mp * Np * Fp * (GBuffer.Specular * 2) * lerp(1, Backlit, saturate(-VoL));????????TT计算中,Tp相当于上面公式中的pow(cos0, 2),Backlit控制这一项的强度,也就是背光时头发的透光度。
float a = 1 / n_prime;
float h = CosHalfPhi * rsqrt(1 + a * a - 2 * a * sqrt(0.5 - 0.5 * CosPhi));
float yt = asin(h / n_prime);
float3 Tp = pow(GBuffer.BaseColor, 0.5 * cos(yt) / CosThetaD);
float f = Hair_F(CosThetaD * sqrt(saturate(1 - h*h)));
float Fp = Pow2(1 - f);
float s = 0.3;
float Np = exp((Phi - PI) / s) / (s * Pow2(1 + exp((Phi - PI) / s)));
S += Mp * Np * Fp * Tp * Backlit;? ? ? ? ?TRT的思路与TT相同,只不过各项的公式不同:
float f = Hair_F(CosThetaD * 0.5);
float Fp = Pow2(1 - f) * f;
float3 Tp = pow(GBuffer.BaseColor, 0.8 / CosThetaD);
float Np = (1/PI) * 2.6 * exp(2 * 2.6 * (CosPhi - 1));
S += Mp * Np * Fp * Tp;? ? ? ? Diffuse
????????漫反射部分用一个hack的方法模拟次表面散射材质:
????????Jd = saturate(NL + w / ( 1 + w )^2);
????????公式w是0-1的一个参数,用来加亮远离光线的面,ue4直接使用1。metallic控制了散射的强度。
?
float3 FakeNormal = normalize(V - N * dot(V,N));
N = FakeNormal;
// Hack approximation for multiple scattering
float Wrap = 1;
float NoL = saturate((dot(N, L) + Wrap) / Square(1 + Wrap));
float DiffuseScatter = (1/PI) * NoL * GBuffer.Metallic;
float Luma = Luminance(GBuffer.BaseColor);
float3 ScatterTint = pow(GBuffer.BaseColor / Luma, 1 - Shadow);
S += sqrt(GBuffer.BaseColor) * DiffuseScatter * ScatterTint;????????眼睛材质
? ? ? ? 眼睛的渲染分为角膜(Cornea),虹膜(Iris)和巩膜(Sclera)。
? ? ? ? 角膜渲染
? ? ? ? 角膜是眼球表面的一层透明薄膜,有较强的反射效果,我们模拟其半透和光泽反射。Specular由其贡献。
? ? ? ? 虹膜和巩膜渲染
? ? ? ? 虹膜是眼球有颜色的部分,巩膜是眼白部分,光线进入瞳孔表面时会发生次表面散射。
????????我们使用用户输入的IrisMask来区分虹膜和巩膜,并对两者进行混合:
lerp(Sclera, Iris, IrisMask)? ? ? ? 虹膜和巩膜的贡献最终设置到Transmission部分。
? ? ? ? 对于虹膜而言,我们使用偏移的法线表现视差:
float IrisNoL = saturate( dot( IrisNormal, L ) );
float Power = lerp( 12, 1, IrisNoL );
float Caustic = 0.8 + 0.2 * ( Power + 1 ) * pow( saturate( dot( CausticNormal, L ) ), Power );
float Iris = IrisNoL * Caustic;? ? ? ? 对于巩膜而言,我们直接认为其为白色,因此只需考虑光线的影响,即计算法线和灯光方向的点积:
float Sclera = NoL;? ? ? ? 环境光照
? ? ? ? 在环境光部分,基于图像的部分包括了天光(Sylight)和反射捕获(Reflection Capture),这两者可以是实时捕获的,也可以是离线指定的。
????????其中,反射捕获就是我们常规意义上理解的IBL中的HDR图像,它给定了局部的反射捕获结果。在场景中,选取最近的反射捕获,并支持在不同的反射球之间过渡。
? ? ? ? 天光是ue4单独引入的概念,可以简单地理解为来自天空的光照,而不像反射捕获仅作用于局部。严格意义上,从来源来看,天光不算间接光,它更像是来自天空的多个方向的环境直接光源,而不是经过了多次反弹的间接光照的颜色,虽然我们在计算Specular IBL仍然会尝试采样天光的立方体贴图。这是因为我们在烘焙光照时可以计算来自天光的多次反弹。
? ? ? ? 作为环境分量,为了改善漏光和提升明暗层次感,Skylight使用了BentNormal修正法线方向,并包含了Visiblity/Occlusion信息。
?
