介绍
隐式曲面渲染的方法:
- 间接渲染:离散为网格,体素或者点云。一般使用光栅化,放大时会出现不光滑的情况。
- 直接渲染:光线追踪。速度慢。
区间算术(Interval Arithmetic)和仿射算术(Affine Arithmetic)主要使用在数值计算中。是自验证(self-validated)的算术方法。
隐式曲面光线追踪
隐式曲面公式:
f
(
x
,
y
,
z
)
=
0
f(x, y, z) = 0
f(x,y,z)=0
光线:
p
(
t
)
=
o
+
t
d
p(t) = o + td
p(t)=o+td
光线追踪主要是求曲面和光线的交点, 即求解方程:
f
(
t
)
=
f
(
o
x
+
t
d
x
,
o
y
+
t
d
y
,
o
z
+
t
d
z
)
=
0
f(t) = f(o_{x} + td_{x}, o_{y} + td_{y},o_{z} + td_{z}) = 0
f(t)=f(ox?+tdx?,oy?+tdy?,oz?+tdz?)=0
的最小的根,且t>0
求解复杂方程的根可以使用迭代的数值方法例如牛顿迭代法,但是只可以处理单调情况。对于非单调情况,可以使用区间分析的方法。
Interval Arithmetic
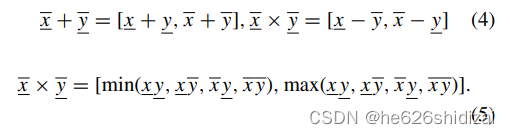
Reduced Affine Arithmetic
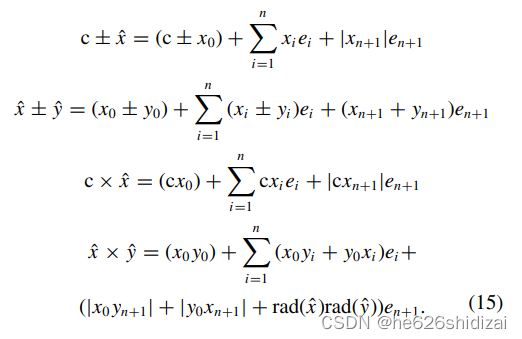
AA相比IA具有更紧致的包围盒,Revised AA[1]可以固定误差元的数量,效率更高。
算法流程
构建曲面的AABB包围盒, 使用光线与包围盒求交,得到入射位置penter和出射位置pexit, 仿射算术aa_t= [0, 1], 那么penter + aa_t * pexit就是包围盒中的光线。
求交测试:将penter + aa_t * pexit的三个分量带入曲面公式,得到的区间如果包含0, 那么表示光线和曲面有交
将aa_t看作参数区间,如果求交测试通过,细分参数区间直到达到指定的细分深度,取区间中一点t0, 根据penter + t0 * pexit得到交点位置。
参考
[1]MESSINE F.: Extentions of affine arithmetic: Application to unconstrained global optimization. Journal of Universal Computer Science 8, 11 (2002), 992–1015.
[2]Knoll A, Hijazi Y, Kensler A, et al. Fast ray tracing of arbitrary implicit surfaces with interval and affine arithmetic[C]//Computer Graphics Forum. Oxford, UK: Blackwell Publishing Ltd, 2009, 28(1): 26-40.
