1.向量
1.1 向量的运算
| 运算 | 公式 |
|---|---|
| 矢量和标量的乘/除法 | k v = ( k v x , k v y , k v z ) k\mathbf{v}=(kv_x,kv_y,kv_z) kv=(kvx?,kvy?,kvz?) |
| 矢量的加/减法 | a + b = ( a x + b x , a y + b y , a z + b z ) \mathbf{a}+\mathbf{b}=(a_x+b_x,a_y+b_y,a_z+b_z) a+b=(ax?+bx?,ay?+by?,az?+bz?) |
| 矢量的模 | ∣ a ∣ = a x 2 + a y 2 + a z 2 \vert\mathbf{a}\vert=\sqrt{a_x^2+a_y^2+a_z^2} ∣a∣=ax2?+ay2?+az2?? |
| 矢量的点积 | a ? b = a x b x + a y b y + a z b z = ∣ a ∣ ∣ b ∣ cos ? θ \mathbf{a·b}=a_xb_x+a_yb_y+a_zb_z=\vert\mathbf{a}\vert\vert\mathbf{b}\vert\cos\theta a?b=ax?bx?+ay?by?+az?bz?=∣a∣∣b∣cosθ |
| 矢量的叉积 | a × b = ( a y b z ? a z b y , a z b x ? a x b z , a x b y ? a y b x ) \mathbf{a×b}=(a_yb_z-a_zb_y,a_zb_x-a_xb_z,a_xb_y-a_yb_x) a×b=(ay?bz??az?by?,az?bx??ax?bz?,ax?by??ay?bx?) |
从几何意义上看:
(1)矢量与标量的乘/除法意味着对矢量进行缩放
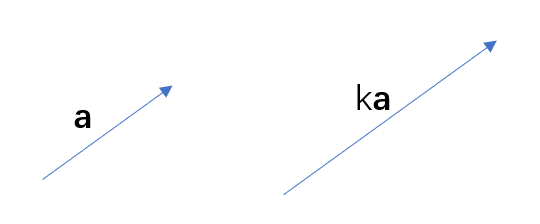
(2)矢量的加/减法意味着矢量间的位置偏移

(3)矢量的模意味着矢量在空间中的长度

(4)矢量的点积意味着一个矢量在另一个矢量方向上的投影再乘以后者的长度
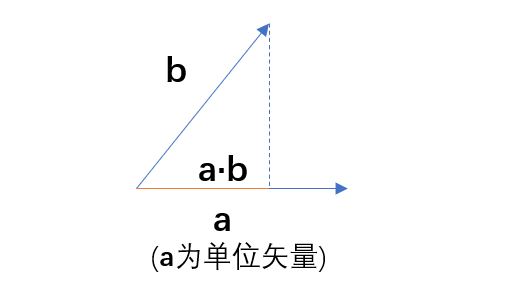
(5)矢量的叉积意味着一个同时垂直于两矢量的新矢量,长度是两矢量的模乘以它们之间夹角的余弦值

矢量叉乘得到的新矢量方向在左手坐标系和右手坐标系中并不相同,但仅仅影响在三维空间中的表现,数学计算的结果并无差异。
1.2 Vector3类
在 Unity 中,和向量有关的类有 Vector2、Vector3 和 Vector4,分别对应不同维度的向量。
下面是Vector3类中的成员变量和常用方法。

2.矩阵
2.1 矩阵的运算
| 运算 | 公式 |
|---|---|
| 矩阵与标量的乘法 | k M = k [ a b c d e f ] = [ k a k b k c k d k e k f ] k\mathbf{M}=k\begin{bmatrix}a & b & c \\ d & e & f\end{bmatrix}=\begin{bmatrix}ka & kb & kc \\ kd & ke & kf\end{bmatrix} kM=k[ad?be?cf?]=[kakd?kbke?kckf?] |
| 矩阵与矩阵的乘法 | A B = [ a 1 b 1 c 1 ] [ a 2 b 2 c 2 ] = [ a 1 a 2 a 1 b 2 a 1 c 2 b 1 a 2 b 1 b 2 b 1 c 2 c 1 a 2 c 1 b 2 c 1 c 2 ] \mathbf{AB}=\begin{bmatrix}a_1 \\ b_1 \\ c_1\end{bmatrix}\begin{bmatrix}a_2 & b_2 & c_2\end{bmatrix}=\begin{bmatrix}a_1a_2 & a_1b_2 & a_1c_2 \\ b_1a_2 & b_1b_2 & b_1c_2 \\ c_1a_2 & c_1b_2 & c_1c_2\end{bmatrix} AB=???a1?b1?c1?????[a2??b2??c2??]=???a1?a2?b1?a2?c1?a2??a1?b2?b1?b2?c1?b2??a1?c2?b1?c2?c1?c2????? |
2.2 特殊矩阵
(1)方阵:行数与列数相等的矩阵
[
1
2
3
4
5
6
7
8
9
]
\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}
???147?258?369????
(2)对角矩阵:除了对角元素外,其他所有元素都为0的方阵
[
1
0
0
0
5
0
0
0
9
]
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{bmatrix}
???100?050?009????
(3)单位矩阵:对角元素都为1的对角矩阵
I
=
[
1
0
0
0
1
0
0
0
1
]
\mathbf{I}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
I=???100?010?001????
性质:
任何矩阵与单位矩阵相乘结果都是原来的矩阵
I
M
=
M
\mathbf{IM}=\mathbf{M}
IM=M
(4)转置矩阵:原本的行转为列,原本的列转为行
M
=
[
1
2
3
4
5
6
7
8
9
]
\mathbf{M}= \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}
M=???147?258?369????
M
T
=
[
1
4
7
2
5
8
3
6
9
]
\mathbf{M}^T= \begin{bmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{bmatrix}
MT=???123?456?789????
性质:
矩阵转置的转置等于原矩阵
(
M
T
)
T
=
M
(\mathbf{M}^T)^T=\mathbf{M}
(MT)T=M
矩阵串接的转置等于反向串接各个矩阵的转置
(
A
B
)
T
=
B
T
A
T
(\mathbf{AB})^T=\mathbf{B}^T\mathbf{A}^T
(AB)T=BTAT
(5)逆矩阵:两方阵相乘等于单位矩阵,则两方阵互为逆矩阵
M
M
?
1
=
I
\mathbf{MM}^{-1}=\mathbf{I}
MM?1=I
如果一个矩阵有对应的逆矩阵,则称这个矩阵是可逆的或非奇异的,相反则称不可逆的或奇异的。
性质:
逆矩阵的逆矩阵是原矩阵本身
(
M
?
1
)
?
1
=
M
(\mathbf{M}^{-1})^{-1}=\mathbf{M}
(M?1)?1=M
单位矩阵的逆矩阵是它本身
I
?
1
=
I
\mathbf{I}^{-1}=\mathbf{I}
I?1=I
转置矩阵的逆矩阵是逆矩阵的转置
(
M
T
)
?
1
=
(
M
?
1
)
T
(\mathbf{M}^{T})^{-1}=(\mathbf{M}^{-1})^{T}
(MT)?1=(M?1)T
矩阵串接相乘后的逆矩阵等于反向串接各个矩阵的逆矩阵
(
A
B
)
?
1
=
B
?
1
A
?
1
(\mathbf{AB})^{-1}=\mathbf{B}^{-1}\mathbf{A}^{-1}
(AB)?1=B?1A?1
(6)正交矩阵:一个矩阵乘这个矩阵的转置等于单位矩阵,则称这个矩阵是正交的
M
M
T
=
I
\mathbf{MM}^{T}=\mathbf{I}
MMT=I
如果一个矩阵是正交的,则它的转置矩阵等于逆矩阵
M
T
=
M
?
1
\mathbf{M}^{T}=\mathbf{M}^{-1}
MT=M?1
如果一个矩阵满足各行列向量都是单位向量,且两两垂直,则这个矩阵是正交矩阵
正交基:一组互相垂直的基矢量叫做一组正交基
标准正交基:每个基矢量长度都为1的正交基叫做标准正交基
正交矩阵就是一组标准正交基
2.3 矩阵与线性变换
(1)旋转
在二维坐标系中,对x轴和y轴方向上的单位向量旋转θ度,可以得到如下结果:
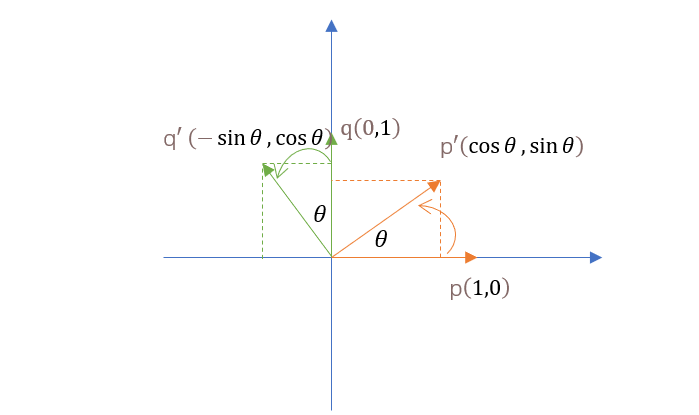
得到二维空间的旋转矩阵:
R
=
[
p
′
q
′
]
=
[
c
o
s
θ
s
i
n
θ
?
s
i
n
θ
c
o
s
θ
]
R=\begin{bmatrix} p' \\ q' \end{bmatrix}=\begin{bmatrix} cosθ & sinθ \\ -sinθ & cosθ \end{bmatrix}
R=[p′q′?]=[cosθ?sinθ?sinθcosθ?]
扩展到三维空间(以左手坐标系为例)
绕z轴旋转
R
z
(
θ
)
=
[
c
o
s
θ
s
i
n
θ
0
?
s
i
n
θ
c
o
s
θ
0
0
0
1
]
R_z(θ)=\begin{bmatrix} cosθ & sinθ & 0 \\ -sinθ & cosθ & 0 \\ 0 & 0 & 1 \end{bmatrix}
Rz?(θ)=???cosθ?sinθ0?sinθcosθ0?001????
绕x轴旋转
R
x
(
θ
)
=
[
1
0
0
0
c
o
s
θ
s
i
n
θ
0
?
s
i
n
θ
c
o
s
θ
]
R_x(θ)=\begin{bmatrix} 1 & 0 & 0 \\ 0 & cosθ & sinθ \\ 0 & -sinθ & cosθ \end{bmatrix}
Rx?(θ)=???100?0cosθ?sinθ?0sinθcosθ????
绕y轴旋转
R
y
(
θ
)
=
[
c
o
s
θ
0
?
s
i
n
θ
0
1
0
s
i
n
θ
0
c
o
s
θ
]
R_y(θ)=\begin{bmatrix} cosθ & 0 & -sinθ \\ 0 & 1 & 0 \\ sinθ & 0 & cosθ \end{bmatrix}
Ry?(θ)=???cosθ0sinθ?010??sinθ0cosθ????
附上绕任意轴旋转的旋转矩阵(可以将变换后的向量
v
′
\mathbf{v'}
v′拆分成平行于旋转轴的向量
v
′
∥
\mathbf{v'}_{∥}
v′∥?和垂直于旋转轴的向量
v
′
⊥
\mathbf{v'}_{⊥}
v′⊥?,利用几何求出
v
\mathbf{v}
v和
v
′
\mathbf{v'}
v′的关系公式,带入三个基向量即可)
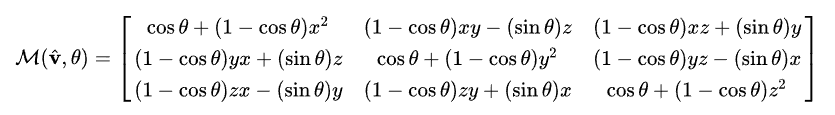
(2)缩放
沿坐标轴缩放比较简单,只需要对矢量各个坐标轴方向上的分量乘以一个常数即可。
[
x
y
z
]
[
k
x
0
0
0
k
y
0
0
0
k
z
]
=
[
k
x
x
k
y
y
k
z
z
]
\begin{bmatrix} x & y & z\end{bmatrix}\begin{bmatrix}k_x & 0 & 0\\0 & k_y & 0\\0 & 0 & k_z\end{bmatrix}=\begin{bmatrix} k_xx & k_yy & k_zz\end{bmatrix}
[x?y?z?]???kx?00?0ky?0?00kz?????=[kx?x?ky?y?kz?z?]
当
k
x
=
k
y
=
k
z
k_x=k_y=k_z
kx?=ky?=kz?时,该缩放称为统一缩放,否则为非统一缩放。
沿任意轴的缩放矩阵(与沿任意轴的旋转矩阵求法类似)

(3)正交投影
当对一个三维空间中的物体进行正交投影时,相当于让垂直于投影平面的分量归零,其他方向上的分量不变。

例如对矢量
v
\mathbf{v}
v分别做xy、xz、yz平面上的正交投影:
v
P
x
y
=
[
x
y
z
]
[
1
0
0
0
1
0
0
0
0
]
=
[
x
y
0
]
\mathbf{vP_{xy}}=\begin{bmatrix} x & y & z\end{bmatrix}\begin{bmatrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 0\end{bmatrix}=\begin{bmatrix} x & y & 0\end{bmatrix}
vPxy?=[x?y?z?]???100?010?000????=[x?y?0?]
v
P
x
z
=
[
x
y
z
]
[
1
0
0
0
0
0
0
0
1
]
=
[
x
0
z
]
\mathbf{vP_{xz}}=\begin{bmatrix} x & y & z\end{bmatrix}\begin{bmatrix}1 & 0 & 0\\0 & 0 & 0\\0 & 0 & 1\end{bmatrix}=\begin{bmatrix} x & 0 & z\end{bmatrix}
vPxz?=[x?y?z?]???100?000?001????=[x?0?z?]
v
P
y
z
=
[
x
y
z
]
[
0
0
0
0
1
0
0
0
1
]
=
[
0
y
z
]
\mathbf{vP_{yz}}=\begin{bmatrix} x & y & z\end{bmatrix}\begin{bmatrix}0 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{bmatrix}=\begin{bmatrix} 0 & y & z\end{bmatrix}
vPyz?=[x?y?z?]???000?010?001????=[0?y?z?]
利用数学归纳法可以求出任意平面的正交投影矩阵(
n
\mathbf{n}
n为垂直于投影平面的单位向量)
P
n
=
[
1
?
n
x
2
?
n
x
n
y
?
n
x
n
z
?
n
x
n
y
1
?
n
y
2
?
n
y
n
z
?
n
x
n
z
?
n
z
n
y
1
?
n
z
2
]
\mathbf{P_n}=\begin{bmatrix} 1-n_x^2 & -n_xn_y & -n_xn_z\\ -n_xn_y & 1-n_y^2 & -n_yn_z \\ -n_xn_z & -n_zn_y & 1-n_z^2\end{bmatrix}
Pn?=???1?nx2??nx?ny??nx?nz???nx?ny?1?ny2??nz?ny???nx?nz??ny?nz?1?nz2?????
(4)镜像
镜像矩阵与正交投影矩阵非常相似,唯一的区别是正交投影矩阵缩放因子是0,镜像矩阵缩放因子是-1
P
m
=
[
1
?
2
n
x
2
?
2
n
x
n
y
?
2
n
x
n
z
?
2
n
x
n
y
1
?
2
n
y
2
?
2
n
y
n
z
?
2
n
x
n
z
?
2
n
z
n
y
1
?
2
n
z
2
]
\mathbf{P_m}=\begin{bmatrix} 1-2n_x^2 & -2n_xn_y & -2n_xn_z\\ -2n_xn_y & 1-2n_y^2 & -2n_yn_z \\ -2n_xn_z & -2n_zn_y & 1-2n_z^2\end{bmatrix}
Pm?=???1?2nx2??2nx?ny??2nx?nz???2nx?ny?1?2ny2??2nz?ny???2nx?nz??2ny?nz?1?2nz2?????
(5)切变
所谓切变就是对物体进行扭曲变换,但物体的面积(体积)不会发生改变。

在二维空间中的切变矩阵如下(s是切变因子):
H
x
(
s
)
=
[
1
0
s
1
]
\mathbf{H_x(s)}=\begin{bmatrix}1 & 0\\ s & 1\end{bmatrix}
Hx?(s)=[1s?01?]
H
y
(
s
)
=
[
1
s
0
1
]
\mathbf{H_y(s)}=\begin{bmatrix}1 & s\\ 0 & 1\end{bmatrix}
Hy?(s)=[10?s1?]
可以理解为矢量的一个坐标轴上的分量被另一个轴的分量所改变。以
H
x
(
s
)
\mathbf{H_x(s)}
Hx?(s)为例,一个矢量的y越大,x的偏移就会越大(
x
′
=
x
+
s
y
x'=x+sy
x′=x+sy)
在三维空间中的切变矩阵如下:
H
x
y
(
s
,
t
)
=
[
1
0
0
0
1
0
s
t
1
]
\mathbf{H_xy(s,t)}=\begin{bmatrix}1 & 0 & 0\\ 0 & 1 & 0 \\s & t & 1\end{bmatrix}
Hx?y(s,t)=???10s?01t?001????
H
x
z
(
s
,
t
)
=
[
1
0
0
s
1
t
0
0
1
]
\mathbf{H_xz(s,t)}=\begin{bmatrix}1 & 0 & 0\\ s & 1 & t \\0 & 0 & 1\end{bmatrix}
Hx?z(s,t)=???1s0?010?0t1????
H
y
z
(
s
,
t
)
=
[
1
s
t
0
1
0
0
0
1
]
\mathbf{H_yz(s,t)}=\begin{bmatrix}1 & s & t\\ 0 & 1 & 0 \\0 & 0 & 1\end{bmatrix}
Hy?z(s,t)=???100?s10?t01????
2.4 矩阵行列式
有如下所示的矩阵M
M
=
[
m
11
m
12
m
13
m
21
m
22
m
23
m
31
m
32
m
33
]
\mathbf{M}=\begin{bmatrix}m_{11} & m_{12} & m_{13}\\ m_{21} & m_{22} & m_{23} \\m_{31} & m_{32} & m_{33}\end{bmatrix}
M=???m11?m21?m31??m12?m22?m32??m13?m23?m33?????
则它的行列式可以表示为
∣
M
∣
=
∣
m
11
m
12
m
13
m
21
m
22
m
23
m
31
m
32
m
33
∣
=
m
11
m
22
m
33
+
m
12
m
23
m
31
+
m
13
m
21
m
32
?
m
13
m
22
m
31
?
m
23
m
32
m
11
?
m
33
m
12
m
21
\mathbf{|M|}=\left|\begin{array}{cccc} m_{11} & m_{12} & m_{13}\\ m_{21} & m_{22} & m_{23} \\m_{31} & m_{32} & m_{33}\end{array}\right|=m_{11}m_{22}m_{33}+m_{12}m_{23}m_{31}+m_{13}m_{21}m_{32}-m_{13}m_{22}m_{31}-m_{23}m_{32}m_{11}-m_{33}m_{12}m_{21}
∣M∣=∣∣∣∣∣∣?m11?m21?m31??m12?m22?m32??m13?m23?m33??∣∣∣∣∣∣?=m11?m22?m33?+m12?m23?m31?+m13?m21?m32??m13?m22?m31??m23?m32?m11??m33?m12?m21?
性质:
(1)行列式的转置等于它本身
D
T
=
D
\mathbf{D}^T=\mathbf{D}
DT=D
(2)互换行列式的两行(列),行列式变号

(3)行列式中某一行(列)中所有元素都乘以同一数k,等于k乘此行列式
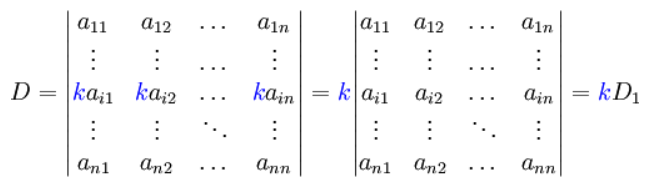
(4)行列式中如果有两行(列)元素成比例, D = 0 \mathbf{D}=0 D=0
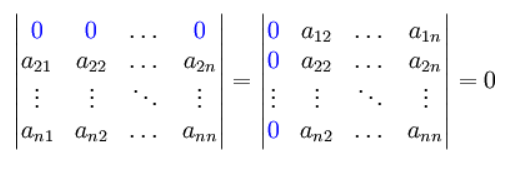
(5)若行列式中某一行(列)的元素都是两数之和,则此行列式可以拆分为两个相加的行列式

(6)把行列式的某一行(列)的各元素乘以同一数后加到另一行(列)对应元素上,行列式不变
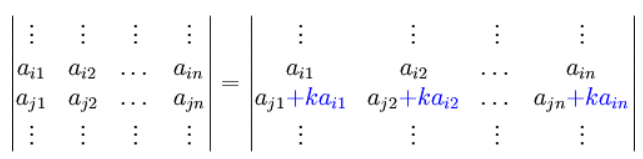
2.5 余子式与代数余子式
余子式: 在n阶行列式中,划去元 a i j a_{ij} aij?所在的第i行与第j列的元,剩下的元不改变原来的顺序所构成的n-1阶行列式称为元 a i j a_{ij} aij?的余子式。数学上记作 M i j \mathbf{M_ij} Mi?j。
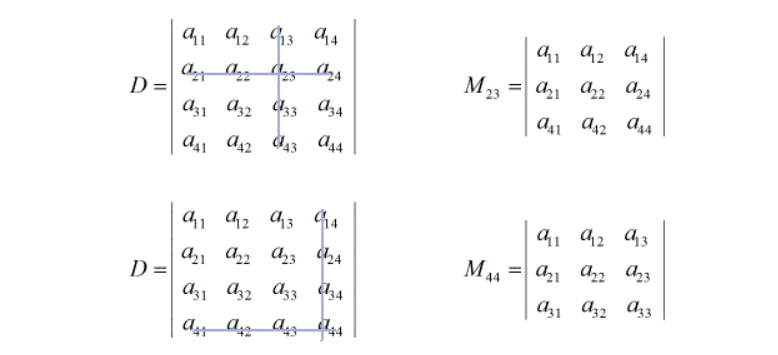
代数余子式: A i j = ( ? 1 ) ( i + j ) M i j A_{ij}=(-1)^{(i+j)}M_{ij} Aij?=(?1)(i+j)Mij?,其中 A i j A_{ij} Aij?就是 a i j a_{ij} aij?的代数余子式。(具体可以看这篇文章:传送门)
行列式与代数余子式的关系:
行列式等于它任意一行(列)的各元素与其对应的代数式余子式乘积之和

2.6 伴随矩阵
方阵
A
=
(
a
i
j
)
n
×
n
A=(a_{ij})_{n×n}
A=(aij?)n×n?的各元素的代数余子式
A
i
j
A_{ij}
Aij?所构成的如下矩阵
A
?
A^*
A?:
A
?
=
[
A
11
A
21
.
.
.
A
n
1
A
12
A
22
.
.
.
A
n
2
?
?
?
A
1
n
A
2
n
.
.
.
A
n
n
]
A^*=\begin{bmatrix} A_{11} & A_{21} & ... & A_{n1}\\ A_{12} & A_{22} & ... & A_{n2} \\\vdots & \vdots & & \vdots\\ A_{1n} & A_{2n} & ... & A_{nn}\end{bmatrix}
A?=??????A11?A12??A1n??A21?A22??A2n??.........?An1?An2??Ann????????
(注意这其实是各元素的代数余子式组成的矩阵的转置)
性质:
矩阵A与其伴随矩阵的乘积为 ,行列式的值乘以单位矩阵
A
A
?
=
A
?
A
=
∣
A
∣
I
AA^*=A^*A=|A|I
AA?=A?A=∣A∣I
根据逆矩阵的性质
A
A
?
1
=
I
AA^{-1}=I
AA?1=I
可以得出
A
?
1
=
A
?
∣
A
∣
A^{-1}=\frac{A^*}{|A|}
A?1=∣A∣A??
当
∣
A
∣
≠
0
|A|≠0
∣A∣?=0时,矩阵可逆,反之不可逆。不可逆矩阵又称奇异矩阵。
2.7 齐次坐标
齐次坐标就是在原本的三维向量中增加一个 w w w分量,即 ( x , y , z , w ) (x,y,z,w) (x,y,z,w)。当 w = 1 w=1 w=1时,表示的是标准三维空间中的坐标。当 w = 0 w=0 w=0时,表示的是标准三维空间中的方向。任何齐次坐标转换到标准三维空间的坐标都为 ( x / w , y / w , z / w ) (x/w,y/w,z/w) (x/w,y/w,z/w)。
引入齐次坐标后,我们就可以进行平移变换
平移
[
x
y
z
1
]
[
1
0
0
0
0
1
0
0
0
0
1
0
Δ
x
Δ
y
Δ
z
1
]
=
[
x
+
Δ
x
y
+
Δ
y
z
+
Δ
z
1
]
\begin{bmatrix} x & y& z& 1 \end{bmatrix}\begin{bmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\0 & 0 & 1 & 0\\ \Delta x & \Delta y & \Delta z & 1\end{bmatrix}=\begin{bmatrix} x+\Delta x & y+\Delta y& z+\Delta z & 1 \end{bmatrix}
[x?y?z?1?]?????100Δx?010Δy?001Δz?0001??????=[x+Δx?y+Δy?z+Δz?1?]
当
w
w
w分量为0时,就会使平移失效,但不会影响其他变换。
透视投影
[ x y z 1 ] [ 1 0 0 0 0 1 0 0 0 0 1 1 / d 0 0 0 0 ] = [ x y z z / d ] \begin{bmatrix} x & y& z& 1 \end{bmatrix}\begin{bmatrix}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\0 & 0 & 1 & 1/d\\ 0 & 0 & 0 & 0\end{bmatrix}=\begin{bmatrix} x & y& z & z/d \end{bmatrix} [x?y?z?1?]?????1000?0100?0010?001/d0??????=[x?y?z?z/d?]
仿射变换
通俗的讲就是线性变换+平移
可以参考这篇文章传送门
变换的分类
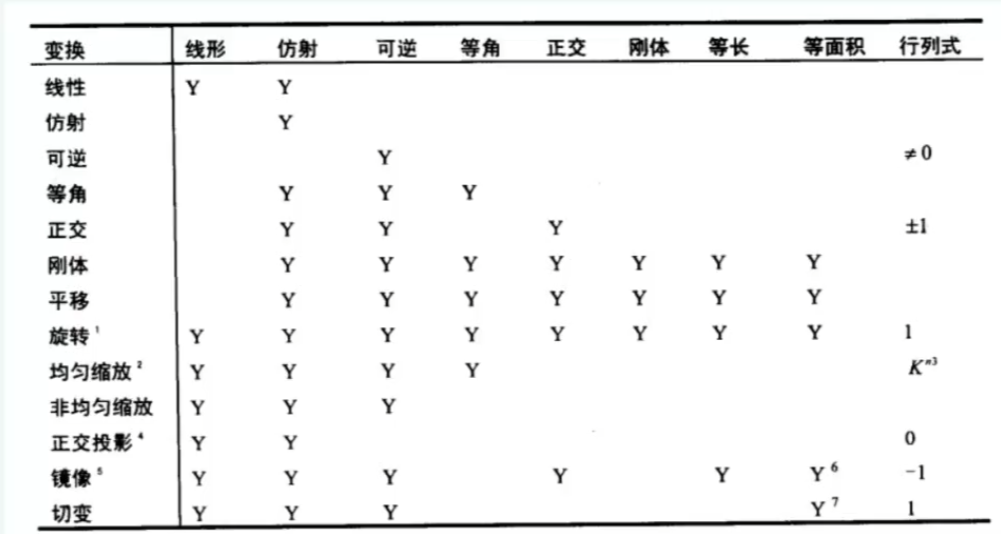
2.8 Unity中的透视投影与正交投影
首先需要注意的一点是Unity中的观察空间采用的是右手坐标系,因此在变换过程中会采用列向量右乘的方式。
透视投影

Unity中的透视投影矩阵:

其中,
A
s
p
e
c
t
Aspect
Aspect表示的是视锥体的近平面或远平面宽高之比。即:
A
s
p
e
c
t
=
n
e
a
r
C
l
i
p
P
l
a
n
e
W
i
d
t
h
n
e
a
r
C
l
i
p
P
l
a
n
e
H
i
g
h
t
Aspect=\frac{nearClipPlaneWidth}{nearClipPlaneHight}
Aspect=nearClipPlaneHightnearClipPlaneWidth?
或
A
s
p
e
c
t
=
f
a
r
C
l
i
p
P
l
a
n
e
W
i
d
t
h
f
a
r
C
l
i
p
P
l
a
n
e
H
i
g
h
t
Aspect=\frac{farClipPlaneWidth}{farClipPlaneHight}
Aspect=farClipPlaneHightfarClipPlaneWidth?
如果一个顶点在视锥体内,则变换后的坐标必须满足
x
,
y
,
z
x,y,z
x,y,z都处于
[
?
w
,
w
]
[-w,w]
[?w,w]的区间内。
透视投影矩阵会改变空间的旋向性,即空间会从右手坐标系转换为左手坐标系。这意味着离摄像机越远,z值越大。
正交投影
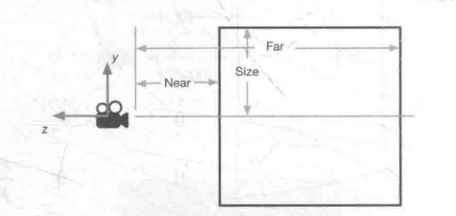
Unity中的正交投影矩阵:

正交投影矩阵同样会改变空间的旋向性。
关于透视投影矩阵和正交投影矩阵详细的推导过程可以参考这篇文章传送门