一、前言
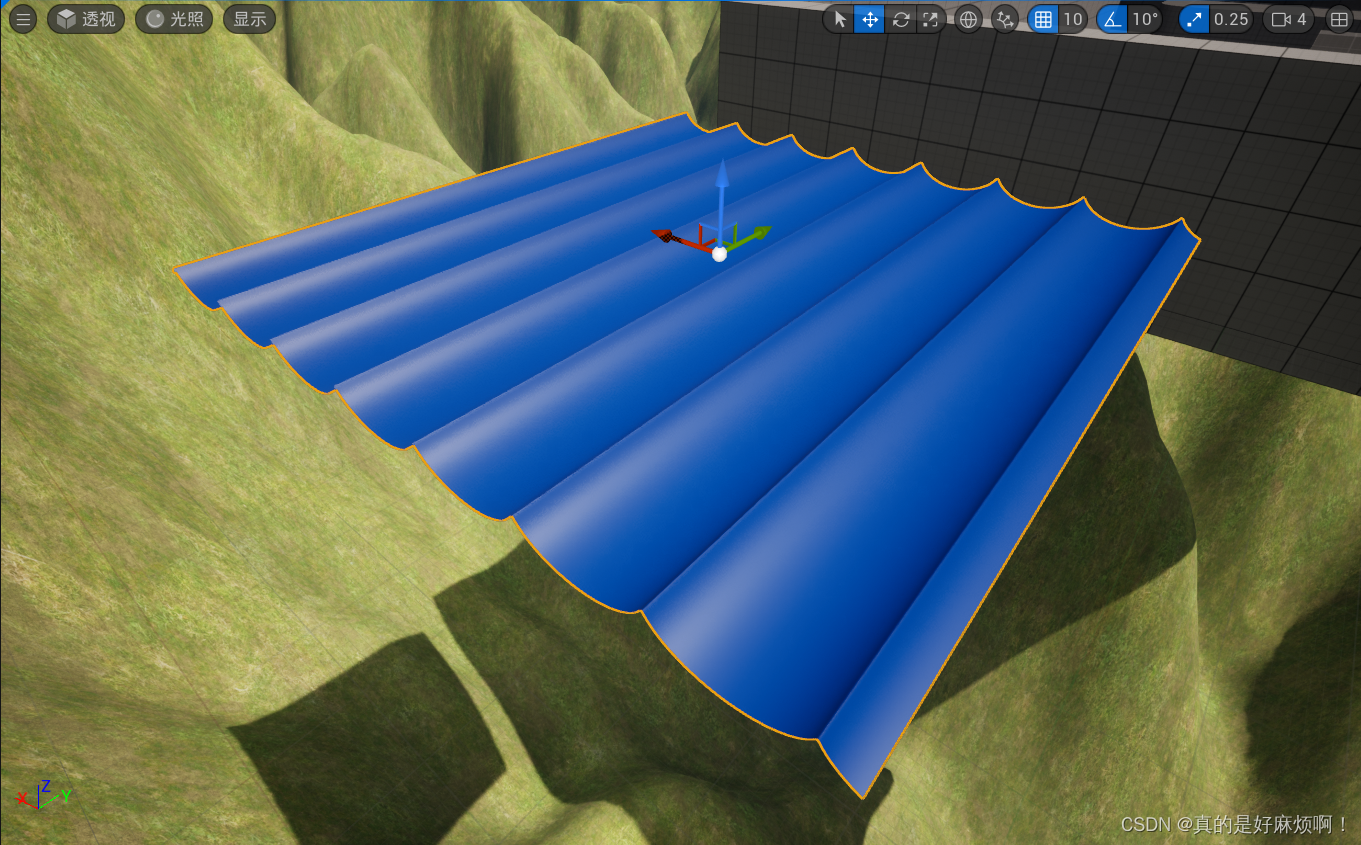
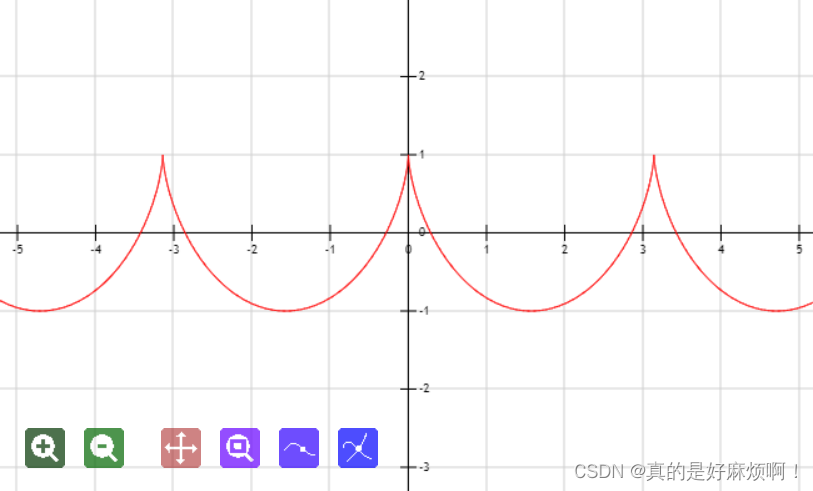
波形叠加是模拟水面的很常见的一种方法,它是通过叠加多个不同周期、不同振幅的周期函数来模拟水体表面的波动。使用的基础波形一般并不是通常的正弦(余弦)波,而是一种名为Gerstner波的特殊波形,与通常的正弦(余弦)波的区别在于,Gerstner波的波峰尖锐而波谷平缓,而且在波峰两侧有收紧的趋势,与真实海洋表面更加接近。波形如下图所示。
二、Gerstner波公式
公式参考Nvidia的《GPU Gems》(第一部)Chapter 1。
链接:https://developer.nvidia.com/gpugems/gpugems/part-i-natural-effects/chapter-1-effective-water-simulation-physical-models
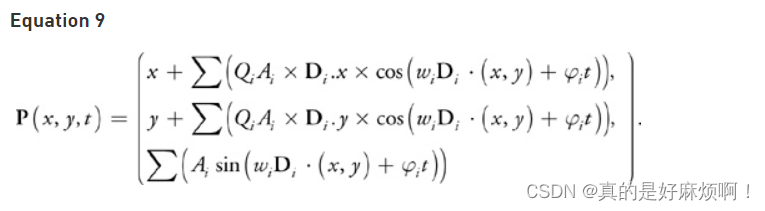
其中:
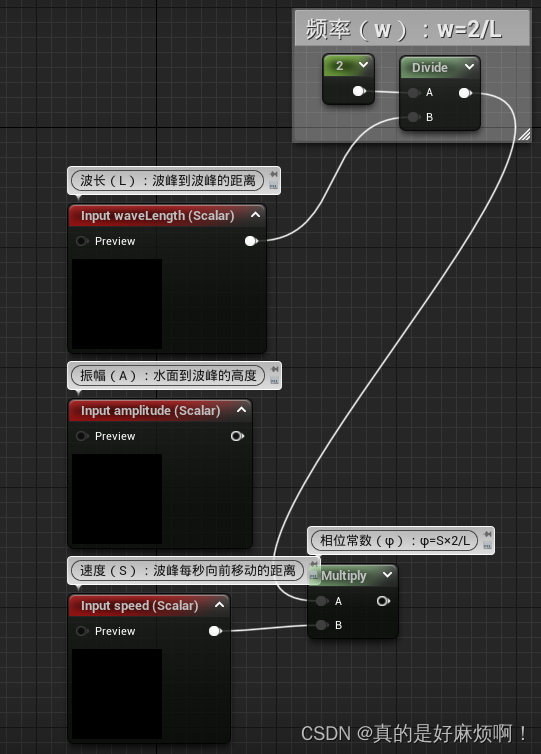
波长(L):波与波峰之间的波峰距离。
频率(w):w与波长L有关,w = 2/L。
振幅 (A):从水平面到波峰的高度。
速度(S):波峰每秒向前移动的距离。将速度表示为相位常数φ很方便,其中 φ = S x 2/L。
方向 (D):垂直于波峰沿波峰行进的波前的水平矢量。
波浪陡度(Q):Q如果为0,则产生的是通常的正弦波,而如果Q = 1/(wA),则生成的是尖锐的波峰,如果继续提高Q,则会导致波峰形成环形。
时间变量(t):不断变化的时间变量,用以产生波移动的效果。
上图函数是对于多个不同Gerstner波的总和函数,这里将它写成单个波的公式则为:
对于波面上的一点P(这里以坐标系z轴朝上),有
Px = x + Q×A×Dx×cos(w×D·(x,y) + φ×t);
Py = y + Q×A×Dy×cos(w×D·(x,y) + φ×t);
Pz = A×sin(w×D·(x,y) + φ×t);
这里先用Shader做下测试(OpenGL中y轴朝上,所以上述函数中Py和Pz需要互换一下):


可见截面与前言中图所绘波形相同。
三、在UE5中实现
1、Gerstner波的实现
接着打开UE5,新建或打开一个项目,在左上角选择建模模式。
选择Rect,创建一个宽度、深度为10001000,宽度细分、深度细分为500500(最大细分似乎只能500)的平面。
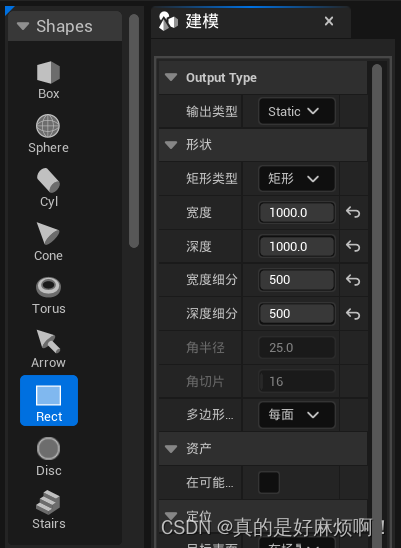

接着在内容管理器中新建一个材质函数,材质函数相当于将一系列材质操作封装成一个有输入和输出的函数,可以在多个材质中调用,避免这一系列材质操作重复编写。
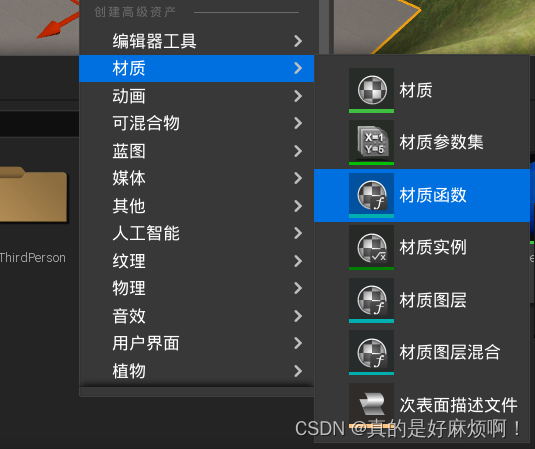
接着双击打开新建的材质函数,在材质图表上右键,并输入input,选择FunctionInput节点。点击出现的红色节点,在细节面板的输入类型中可以设置输入值的类型,这里主要就用两种,一种是标量(float),另一种是向量2(vec2)。
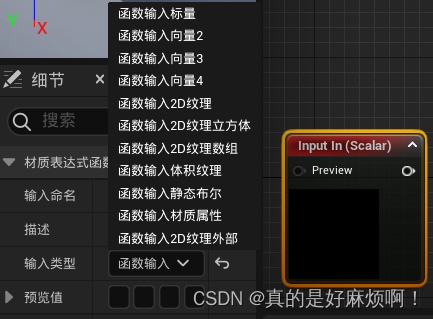
根据函数公式,创建输入值对应的FunctionInput节点。
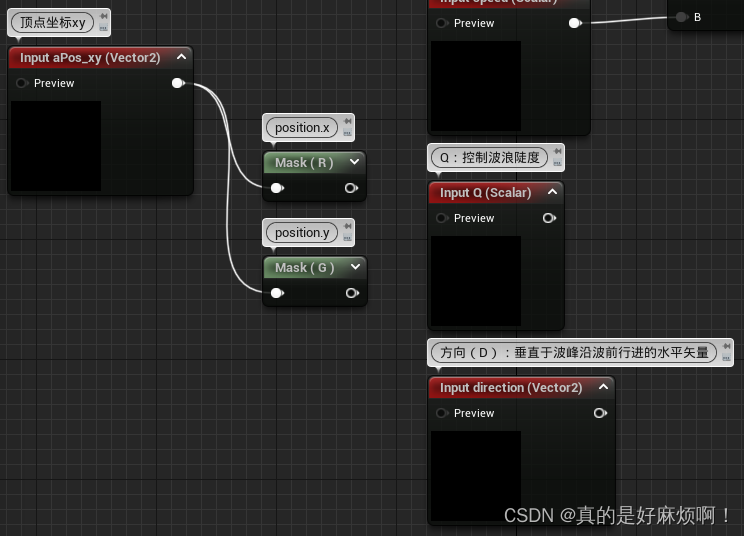
这里介绍几种需要用到的节点:
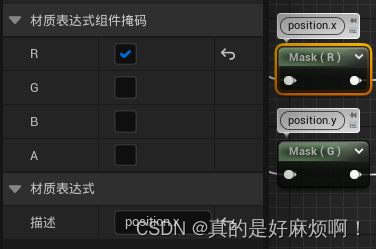
Mask
用于分离出向量(vector)的各个通道,在细节面板上可以勾选需要分离出的通道,假设仅勾选R,则输出的是x的值,如果勾选RG,则输出的是二维向量(x,y),其他以此类推。
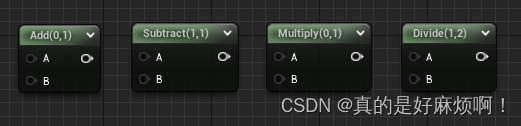
Add、Subtract、Multiply、Divide
加、减、乘、除,A +/-/×/÷ B。
Normalize
向量标准化,就是将向量转化为模为1的向量。
Dot
向量点乘,点乘概念请自行搜索。
Sine
正弦函数。

Cosine
余弦函数。
Time
获取一个时间。
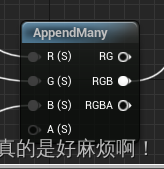
AppendMany
将多个值合成向量输出。
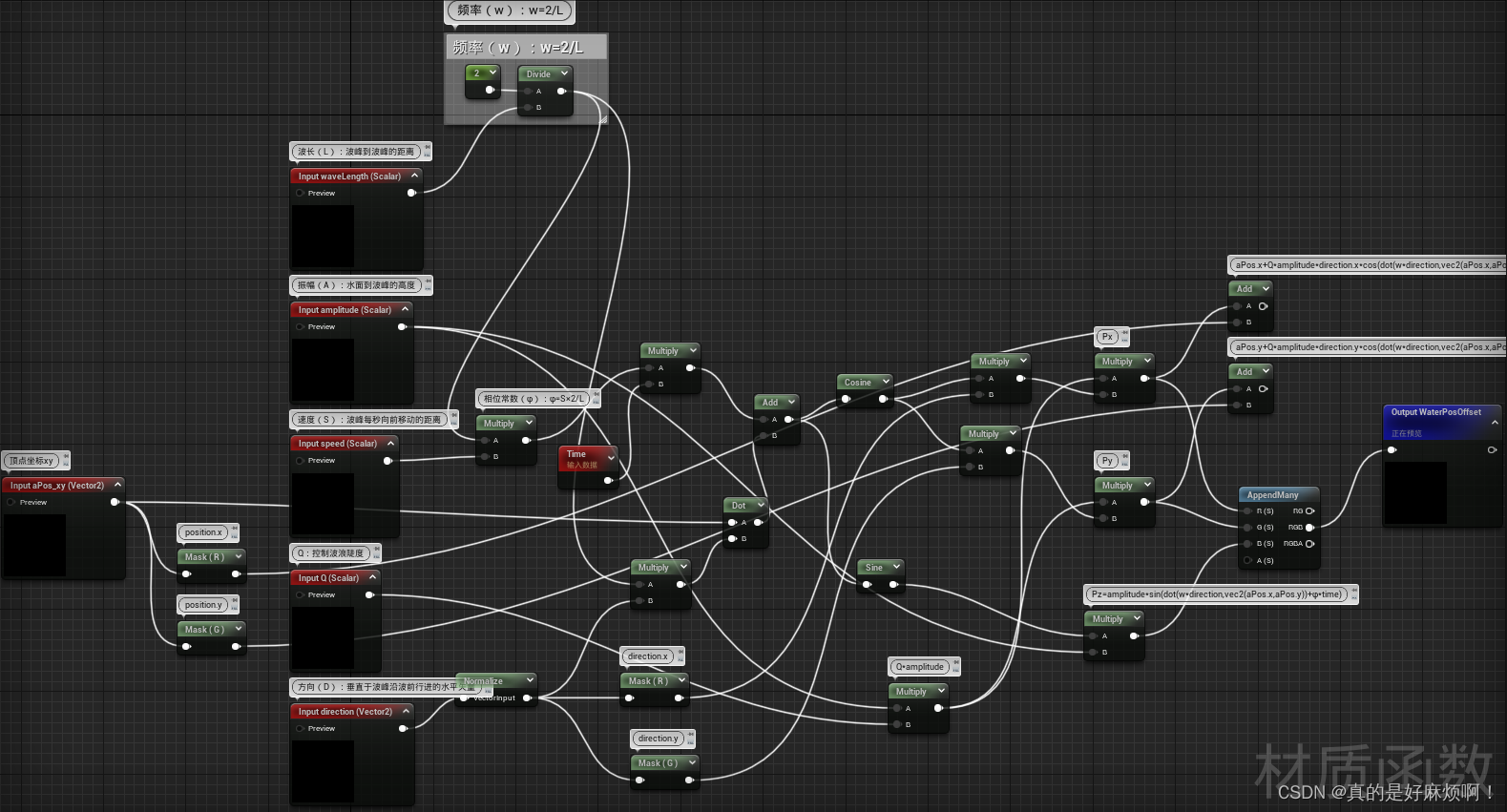
接着用节点将之前的单个波的函数表示出来。这里注意,之前Px和Py函数中需要加上x或y,在这里不需要,原因之后会讲。另外建议将Sine和Cosine节点的细节面板中的句号键设置为2π(默认是1.0,因为是float,设置为2π实际值应该输入6.283185),这个值表示的是一个周期的长度,设置为2π符合习惯。完成后保存。
接着在内容管理器中,新建一个材质,并双击打开。
这里先创建一个基础颜色,在材质图表上右键,并输入constant,选择Constant4Vector节点,双击打开取色器选择一个合适的颜色,然后将此节点连上材质结果节点中的基础颜色。
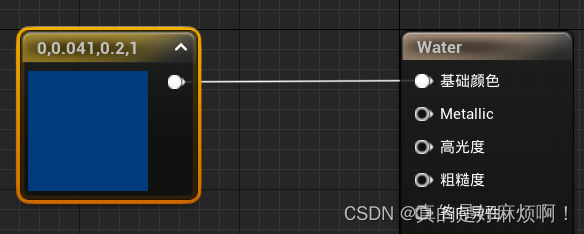
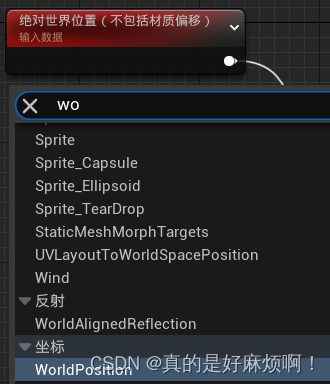
然后点击左下角内容侧滑菜单,打卡内容管理器,将其中之前的材质函数拖入材质图表,图表中出现了材质函数对应的节点。然后右键输入world,选择WorldPosition节点,然后点击在细节面板中将着色器偏移设置为绝对世界坐标(排除材质着色器偏移)。
另外参数方面,float使用Constant,vec2使用Constant2Vector。将参数关联上材质函数的输入,然后材质函数的输出关联上材质结果节点中的全局位置偏移。都关联上后保存。
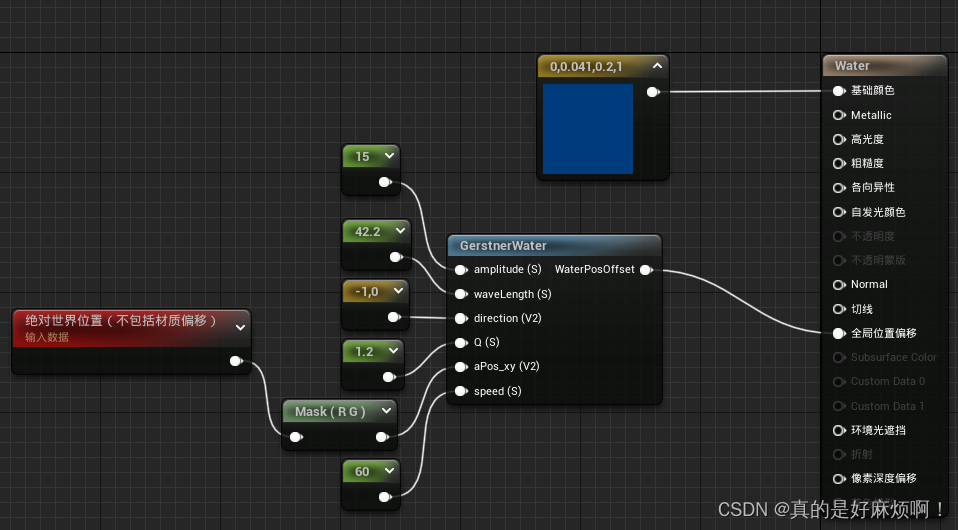
然后回到场景界面,给创建的平面添加这个材质,可以看见平面产生了波动,如果波动效果不对,则适当的调节一下输入的参数。

这里解释一下之前说的为什么不需要加上x或y,因为材质函数的输出关联上的全局位置偏移是在原坐标的基础上再加上连上的值,即原坐标是(x,y,z),材质函数的输出是(x1,y1,z1),则最终的结果则是(x+x1,y+y1,z+z1),如果依照Px和Py函数再加上x或y,则会导致整体多偏移了一个x或y,效果就会像图中一样,模型自身坐标轴还在原位,但显示的已经跑到别的地方去了。

2、对应法线的实现
这个时候的平面在不同角度看还是会显得很平,并不像表面在波动的样子,这是因为材质缺少法线,无法与光照形成阴影。
在《GPU Gems》1.2.2中阐述了求法线的方法,对周期函数求偏x和偏y的偏导数,分别为副法线(binormal)和切线(tangent),这里分别用B和T表示,然后将B和T做叉乘,求得的向量即为法线(normal),这里用N表示。
偏导数求法这里不过多赘述,简单来说求偏x的偏导数,就是将函数中的x视为变量,y视为常量来进行求导,求偏y的偏导数则与之相反。
这里直接写偏导数结果(注意:点积是化为x1y1+x2y2再来求导):
Bx = 1 - w×Dx×Q×A×Dx×sin(w×D·(x,y) + φ×t);
By = - w×Dx×Q×A×Dy×sin(w×D·(x,y) + φ×t);
Bz = w×Dx×A×cos(w×D·(x,y) + φ×t);
Tx = - w×Dy×Q×A×Dx×sin(w×D·(x,y) + φ×t);
Ty = 1 - w×Dy×Q×A×Dy×sin(w×D·(x,y) + φ×t);
Tz = w×Dy×A×cos(w×D·(x,y) + φ×t);
然后新建一个材质函数,接着用节点将B和T的函数表示出来,过程与上面的差不多。
这里新用到的一个节点是Cross节点,表示将A和B做叉乘。
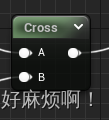
完成之后保存。
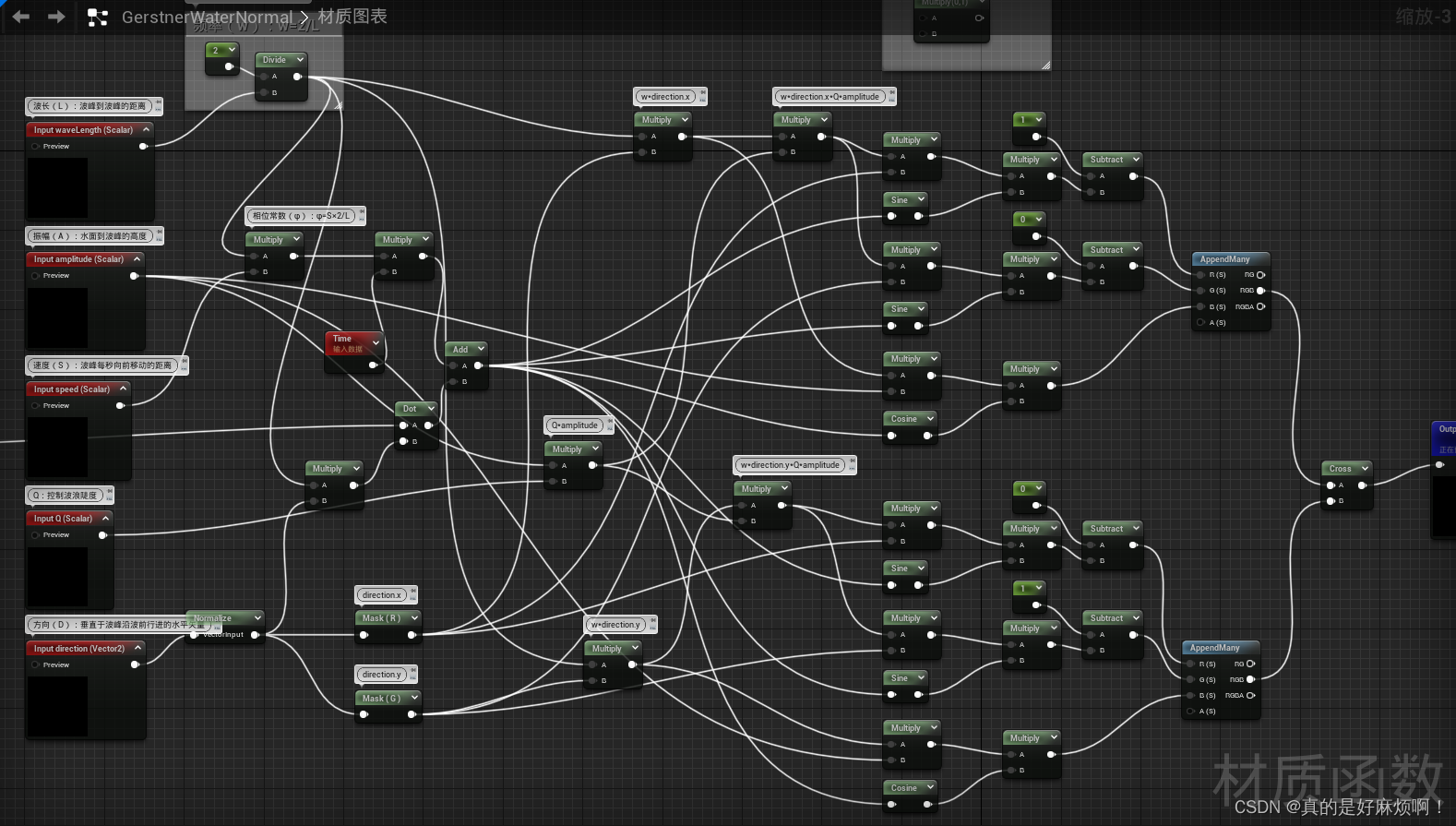
接着打开之前的材质,将这个材质函数拖入材质图表,然后关联上相应的输入参数,将材质函数的输出连上材质结果节点上的Normal,最终的材质图表如图所示。
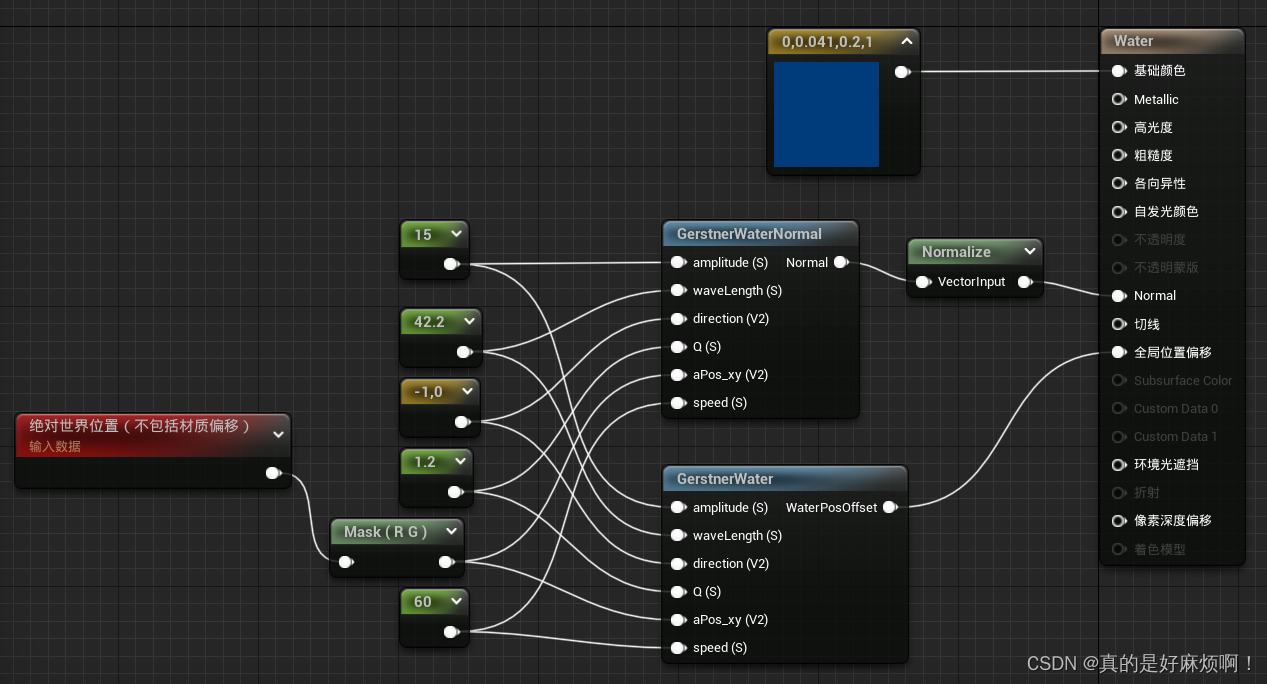
场景中平面的效果如下图,可以很明显的感受到波动的立体感。