开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 游戏开发 -> RL 实践（3）—— 悬崖漫步【QLearning & Sarsa & 各种变体】 -> 正文阅读

[游戏开发]RL 实践（3）—— 悬崖漫步【QLearning & Sarsa & 各种变体】

本文介绍如何用 QLeaning 系列和 Sarsa 系列表格方法解经典的悬崖漫步 (Cliff Walking) 问题
完整代码下载：4_[Gym Custom] Cliff Walking (Q-Learning series and Sarsa series)

1. 悬崖漫步环境 (Cliff Walking)

悬崖漫步是一个离散动作空间，离散状态空间的确定性环境，适合使用 QLeaning 系列和 Sarsa 系列表格方法解决。首先简单介绍悬崖漫步环境，本段引用自《动手学强化学习》第4章
- 这是一个 4x12 的网格世界，每一个网格表示一个状态。智能体的起点是左下角的状态，目标是右下角的状态，智能体在每一个状态都可以采取 4 种动作：上、下、左、右。如果智能体采取动作后触碰到边界墙壁则状态不发生改变，否则就会相应到达下一个状态。环境中有一段悬崖，智能体掉入悬崖或到达目标状态都会结束动作并回到起点，也就是说掉入悬崖或者达到目标状态是终止状态。智能体每走一步的奖励是 ?1，掉入悬崖的奖励是 ?100，到达终止状态奖励为 0
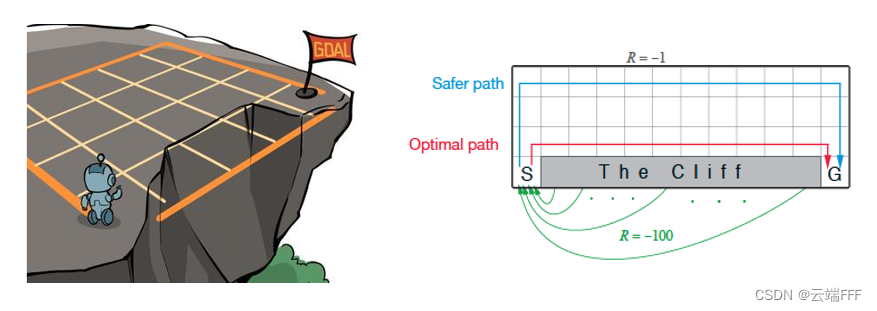
- 注意上图中的 Safer path 和 Optimal path，在 2 节我们会发现 Sarsa 系列方法大多学到前者；Q-Learning 系列方法大多学到后者，相关原因将在第 3 节进一步讨论
下面给出在我利用 gym 实现的 Cliff Walking 环境中运行 Q-Learning 的效果
1. 蓝色圆圈代表 agent，因为我这里仅在轨迹开始时刷新渲染，所以 agent 看起来一直在起点没动
2. 左下角黑色方格，右下角绿色方格，二者间的黑色方格分别代表起点、目标点和悬崖
3. 通过颜色实时渲染相对 $V (s)$ 价值（根据 reward 设置， $V (s)$ 一定都是负数，渲染逻辑是以 $V (s)$ 的最大绝对值为基准，价值越接近基准就越红）
4. 通过渐变颜色直线实时渲染贪心策略，指向是从绿色端指向黑色端
5. 我这里对动作空间增加了 noop 操作，即原地不动，从渲染的策略也可以看出，如果有些方格没有出射直线，就是说 policy 在该位置的 action 为 noop
6. 如图可见，Q-Learning 最终收敛到 Optimal path
关于环境实现细节，请参考：
1. RL gym 环境（2）—— 自定义环境，此文详细介绍了本实验使用环境的设计和代码实现
2. RL gym 环境（3）—— 环境向量化（批量训练），此文介绍了如何并行地在多个环境同时交互，本文最后会利用此方式高效测试算法在多个随机种子上的平均表现

2. 使用 TD 方法求解

大多数表格型 TD Control 方法的框架都差不多，基本都是基于广义策略迭代框架，迭代de进行以下两步至收敛
1. 策略评估：利用 Bellman operator 或 Bellman optimal operator 评估策略价值 $Q_\pi(s,a)$ 或 $Q^*(s,a)$
2. 策略提升：根据当前价值估计贪心地更新策略 $\pi$

因此，不妨先建立一个普适的 TD Learning agent 行为框架作为所有算法的基类

针对可能出现的 Off-policy 方法，定义一个 replay buffer

class ReplayBuffer():
    def __init__(self, size=80):
        self.buffer = []
        self.size = size                # 存储的 transition 总样本量
        
    def push_transition(self, transition):
        if transition not in self.buffer:
            self.buffer.append(transition)
            if len(self.buffer) > self.size:
                self.buffer = self.buffer[-self.size:]
        
    def sample_batch(self, batch_size=5):
        if batch_size > self.size:
            raise ValueError('采样 transition 数超过 buffer 容量')
        return random.sample(self.buffer, min(batch_size, len(self.buffer)))

    def isfull(self):
        return len(self.buffer) == self.size

对于各种 TD Learning 方法而言，除了更新 $Q$ 估计的具体操作不同外，其他几乎都相同。可以先如下抽象出基类

import numpy as np
import gym
import abc
import random

class Slover():
    def __init__(self, env:gym.Env, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None, replay_buffer_size=80):  
        self.env = env      
        self.alpha = alpha
        self.gamma = gamma
        self.epsilon = epsilon
        self.n_action = env.action_space.n
        self.n_observation = env.observation_space.n
        self.Q_table = np.zeros([self.n_observation, self.n_action], dtype=float)
        self.V_table = np.zeros(self.n_observation, dtype=float)
        self.greedy_policy = np.array([np.arange(self.n_action)]*self.n_observation, dtype=object)  # greedy policy，记录每个 observation 下所有最优 action 
        self.policy_is_updated = False                                                              # 当前策略是否匹配最新的 Q_table
        self.rng = np.random.RandomState(seed)                                                      # agent 使用的随机数生成器
        self.replay_buffer = ReplayBuffer(replay_buffer_size)                                       # offline 方法可选用的 replay buffer

    def take_action(self, observation):
        '''
        根据 epsilion-greedy 策略选择动作
        '''
        # 确保策略是匹配最新 Q_table 的
        if not self.policy_is_updated:
            self.update_policy()

        if self.rng.random() < self.epsilon:
            action = self.rng.randint(self.n_action)
        else:
            action = self.rng.choice(self.greedy_policy[observation])
            #action = self.greedy_policy[observation][0]    # 这个等价于 np.argmax(self.Q_table[observation])，速度快一点但忽略了其他最优动作

        return action
    
    def update_policy(self):
        '''
        从 Q_table 导出 greedy policy
        '''
        best_action_value = np.max(self.Q_table, axis=1)
        # 返回一个 ndarray 组成的列表，每个 ndarray 由对应状态下最优动作组成
        self.greedy_policy = np.array([np.argwhere(self.Q_table[i]==best_action_value[i]).flatten() for i in range(self.n_observation)], dtype=object)
        self.policy_is_updated = True

    def update_V_table(self):
        '''
        用 Q_table 及其 greedy policy 计算 V_table, 这个仅用于 UI 显示
        '''
        if not self.policy_is_updated:
            self.update_policy()

        for i in range(self.n_observation):
            greedy_actions = self.greedy_policy[i]
            self.V_table[i] = self.Q_table[i][greedy_actions[0]]    # 贪心策略有 v(s) = E_a[Q(s,a)|s] = max_a Q(s,a|s)

    @abc.abstractmethod
    def update_Q_table(self):
     	'''
        根据所采用的算法具体实现
        '''
        pass

可见这里我们统一使用 $\epsilon$ -greedy 来平衡探索和利用（参考 RL 实践（1）—— 多臂赌博机）。也就是说

对于 on-policy 方法，直接优化一个 $\epsilon$ -greedy 策略；
对于 off-policy 方法，用 $\epsilon$ -greedy 作为行为策略，greedy 作为目标策略，二者同时优化

接下来介绍的不同算法，它们基本就是在用不同方法实例化 update_Q_table 成员方法

关于下文策略评估和显示的进一步说明
1. 由于文本分析的都是 online 方法，下文所有涉及性能评估曲线处，评估的对象都是带 $\epsilon$ 随机的行为策略
2. 下文在地图中实时渲染的策略都是 greedy 策略
3. 如无特殊说明，所有方法参数设为：学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$

2.1 Sarsa

2.1.1 Sarsa 原理

Sarsa 是一种 on-policy 方法。Sarsa 完美体现广义策略迭代思想，每轮迭代中，首先交互得到 transition 样本 $(s, a, r, s^{'})$ ，然后如下应用 Bellman operator 评估一步当前策略
$Q_\pi(s.a) \leftarrow Q_\pi(s,a) + \alpha\big[r + \gamma Q_\pi(s',\pi(s'))-Q_\pi(s,a)\big]$ 最后贪心地进行策略提升。不断迭代以上两步直到收敛为止

Sarsa 算法的伪代码如下
在这里插入图片描述

Sarsa 算法对应的 update_Q_table 方法应如下实现

class Sarsa(Slover):
    def __init__(self, env:gym.Env, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None):
        super().__init__(env, alpha, gamma, epsilon, seed)
    
    def update_Q_table(self, s, a, r, s_, a_):
        td_target = r + self.gamma * self.Q_table[s_, a_]
        td_error = td_target - self.Q_table[s,a]
        self.Q_table[s,a] += self.alpha * td_error
        self.policy_is_updated = False

2.1.2 Sarsa 实验

在 Cliff Walking 环境进行训练，学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$ 。价值收敛过程（三倍快放）和 return 收敛曲线如下

注意收敛到了 Safer path。接下来我们利用环境向量化技巧，让三个使用不用随机种子的 agent 在三个环境中并行交互训练，平均性能如下
下面给出完整代码
1. 单 agent 训练带 UI 渲染：RL_task_practice/4/RL_Sarsa.py
2. 三 agent 并行训练无 UI：RL_task_practice/4/Performence_Sarsa.py

2.2 Expected Sarsa

2.2.1 Expected Sarsa 原理

Expected Sarsa 是一种既可以 On-policy 也可以 Off-policy 使用的算法。Expected Sarsa 是对 Sarsa 的一个改进，二者仅在 TD target 的计算处有区别
1. 标准 Sarsa 计算 TD target 时仅使用了当前策略 $\pi$ 给出的一个 action 计算来计算 $Q_\pi(s,\pi(s'))$
2. Expected Sarsa 计算 TD target 时使用了策略 $\pi$ 所有可能 action 的期望来计算 $\mathbb{E}_{a'\sim\pi(s')}[Q_\pi(s',a')]$
用回溯图来看会更清晰
这只是一个微小的变化，虽然增加了一点计算量，但是带来了极大的好处：
1. 可以作为 off-policy 方法使用了，这意味着可以重用过去的数据，能大幅提升样本效率
  - 一个 value-based 方法能不能用作 off-policy 方法，关键是看我们为目标策略 $\pi$ 构造 TD target 时有没有用到行为策略 $b$ ，如果用到了，那就意味着训练用的数据必须来自收集数据的策略，这样就无法重用过去较差策略收集的数据。
  - 标准 Sarsa 中行为策略 $b$ 决定了构造 TD target 时在 $s^{'}$ 取选择的动作，而 Expected Sarsa 的 TD target 公式中只有目标策略 $\pi$ 出现在期望计算部分，即对行为策略 $b$ 交互得到的 transition $(s, a, r, s^{'})$ 有
    $\begin{aligned} &\text{TD target for sarsa} : &&r + \gamma Q_b(s', b(s')) \\ &\text{TD target for Expected sarsa} : &&r + \gamma \mathbb{E}_{a'\sim\pi(s')}[Q_\pi(s',a')] \end{aligned}$ 因此 Sarsa 不能 off-policy 使用，而 Expected Sarsa 可以
  - 考虑目标策略为 greedy 的特殊情况，这时有
    $\mathbb{E}_{a'\sim\pi(s')}[Q_\pi(s',a')] = \max_{a'} Q(s',a')$ 这正是后面我们将要介绍的 Q-Learning 的更新方式， $max_{a'} Q(s',a')$ 中没有 $\pi$ 了，因此 Q-Learning 可以 off-policy 地使用。事实上，如果我们把行为策略设为 $\epsilon$ -greedy 等有探索性的策略，目标策略设为 greedy，这时的 Expected Sarsa 就是 Q-Learning，也就是说 Q-Learning 其实是 Expected Sarsa 的一个特例
2. Expected Sarsa 中学习率不会影响收敛结果，我们可以放心地将学习率设置为 $\alpha=1$ ，从而大幅加快收敛速度
  这个值得进一步解释一下，简单说
  1. 首先，对于表格型方法，可以证明用 Bellman operator 或 Bellman optimal operator 不断迭代，也就是让每个 $(s, a)$ 处的价值估计不断向 TD traget 移动，价值估计就一定可以收敛（参考强化学习拾遗 —— 表格型方法和函数近似方法中 Bellman 迭代的收敛性分析），这是大前提
  2. Sarsa 有点像随机梯度下降，对于 transition 样本决定的 $s^{'}$ ，我们只向策略给出的一个可行 action $a^{'}$ 对应的 $Q (s^{'}, a^{'})$ 所决定的 TD target 靠近，而这一步运动的方向一定是有偏的，因为 Bellman operator
    $\begin{aligned} Q_{\pi}(s, a) & =\mathbb{E}_{\pi}\left[R_{t+1}+\gamma Q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid s, a\right] \\ & =\sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma \sum_{a^{\prime}} \pi\left(a^{\prime} \mid s^{\prime}\right) Q{\pi}\left(s^{\prime}, a^{\prime}\right)\right] \end{aligned}$ 本身会考虑所有可能的 action。为了良好地收敛，这时学习率 $\alpha$ 必须设得足够小，否则很容易在 sweet point 附近出现反复震荡。如下图所示
    
    这是 $Q$ value 的二维嵌入图，四个蓝色圈代表某状态 $s^{'}$ 处的四个可行 $a^{'}$ 分别对应的 $Q_\pi(s',a')$ ，中间的绿点代表它们的期望，即 Bellman operator 给出的准确的 TD target $\mathbb{E}_{\pi}\left[R_{t+1}+\gamma Q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid s, a\right]$ ，箭头显示了对某个 transition $(s, a, r, s^{'})$ ， $Q_\pi(s,a)$ 从黄点处的初始价值估计开始连续做六次 Bellman Operator 更新的过程。箭头的长度为学习率 $\alpha$ 与 TD error 的乘积，由于同一图中 $\alpha$ 都是常数，因此箭头长度与 TD error （即图中当前位置和目标位置连线长度成正比）。这图应该挺清晰的，就不多解释了
  3. Expected Sarsa 每次给出的 TD target 都是无偏的，因此每一步更新的移动方向都会确定性地减小 TD error，这样下一步更新的移动距离也会相应减小，直到最后 TD error = 0 时，再优化的移动距离也减小到 0，就好像实现了一种自适应学习率的梯度下降优化，如下图所示
    
    可见，我们现在可以放心地使用很大的学习率，而无需担心价值估计的震荡问题，这可以大幅提高价值评估的效率
Expected Sarsa 算法的伪代码和上一节的 Sarsa 完全一致，只需把价值更新那边改成下面这样就行了
$\begin{aligned} Q\left(S_{t}, A_{t}\right) & \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left[R_{t+1}+\gamma \mathbb{E}\left[Q\left(S_{t+1}, A_{t+1}\right) \mid S_{t+1}\right]-Q\left(S_{t}, A_{t}\right)\right] \\ & \leftarrow Q\left(S_{t}, A_{t}\right)+\alpha\left[R_{t+1}+\gamma \sum_{a} \pi\left(a \mid S_{t+1}\right) Q\left(S_{t+1}, a\right)-Q\left(S_{t}, A_{t}\right)\right] \end{aligned}$ Expected Sarsa 算法对应的 update_Q_table 方法应如下实现
```
class SarsaExp(Slover):
    def __init__(self, env:gym.Env, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None):
        super().__init__(env, alpha, gamma, epsilon, seed)
    
    def update_Q_table(self, s, a, r, s_, batch_size=0):    
        if batch_size == 0:     # on-policy
            Q_exp = self.epsilon*self.Q_table[s_].mean() + (1-self.epsilon)*self.Q_table[s_].max()  # epsilon-greedy 策略下的 E_a[Q(s_,a)]
            td_target = r + self.gamma * Q_exp
            td_error = td_target - self.Q_table[s,a]
            self.Q_table[s,a] += self.alpha * td_error
        else:                   # off-policy
            self.replay_buffer.push_transition(transition=(s, a, r, s_))
            transitions = self.replay_buffer.sample_batch(batch_size)
            for s, a, r, s_ in transitions:
                Q_exp = self.epsilon*self.Q_table[s_].mean() + (1-self.epsilon)*self.Q_table[s_].max()  # epsilon-greedy 策略下的 E_a[Q(s_,a)]
                td_target = r + self.gamma * Q_exp
                td_error = td_target - self.Q_table[s,a]
                self.Q_table[s,a] += self.alpha * td_error
        self.policy_is_updated = False
```

2.2.2 Expected Sarsa 实验

2.2.2.1 标准版本

在 Cliff Walking 环境进行训练，学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$ 。价值收敛过程（三倍快放）和 return 收敛曲线如下

注意收敛到了 Safer path。接下来我们利用环境向量化技巧，让三个使用不用随机种子的 agent 在三个环境中并行交互训练，平均性能如下

2.2.2.2 提高学习率

由于前面分析了 Expected Sarsa 的收敛不受学习率影响，下面把学习率改为 $\alpha=1$ 再重复上述实验，结果如下

可见收敛速度大大提升了，这意味着样本效率显著提升

2.2.2.3 使用 replay buffer

前面分析了可以 Off-policy 使用，下面利用 replay buffer 每次迭代随机采样 5 个 transition 重复上述实验，结果如下

可见收敛速度大大提升了，这意味着样本效率显著提升
下面给出完整代码
1. 单 agent 训练带 UI 渲染：RL_task_practice/4/RL_SarsaExp.py
2. 三 agent 并行训练无 UI： RL_task_practice/4/Performance_SarsaExp.py

2.3 N-step Sarsa

2.3.1 N-step Sarsa 原理

N-step Sarsa 是一种 On-policy 算法，但也可以借助重要度采样比改造为 Off-policy 形式。标准 N-step Sarsa 是对 Sarsa 的一个改进，二者仅在 TD target 时展开的步数方面有区别，用回溯图来看会更清晰

可见标准 Sarsa 仅展开了一步，所以它也可称为 1-step Sarsa，n-step Sarsa 是对它的推广。如图可见，我们可以沿着轨迹展开更多步来计算 TD target，这样就能使用更多即时 reward 数据，减小 bootstrap 引入的偏差，但由于每一步展开都有随机性，方差也会随展开步数增加而增大。下面给出 Sarsa 和 N-step Sarsa 的 TD target 计算公式
$\begin{aligned} &\text{TD target for sarsa} : &&G_{t:t+1} \doteq R_{t+1} + \gamma Q_\pi(S_{t+1}, \pi(S_{t+1})) \\ &\text{Bellman update for sarsa} : && Q_\pi(S_t,A_t) \leftarrow Q_\pi(S_t,A_t) + \alpha \big[G_{t:t+1} - Q_\pi(S_t,A_t) \big]\\\\ &\text{TD target for n-step sarsa} : &&G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2}+...+ \gamma^{n-1}R_{t+n} + \gamma^nQ_{\pi}(S_{t+n}, \pi(S_{t+n}))\\ &\text{Bellman update for n-step sarsa} : && Q_\pi(S_t,A_t) \leftarrow Q_\pi(S_t,A_t) + \alpha \big[G_{t:t+n} - Q_\pi(S_t,A_t) \big] \end{aligned}$ 另外，上面的回溯图中还有两个值得注意的点
1. 极限情况下， $\infin$ -step Sarsa 就成为了 MC 方法；
2. N-step Sarsa 可以和 Expected Sarsa 结合得到 N-step Expected Sarsa 方法。

下面给出 N-step Sarsa 的伪代码
在这里插入图片描述
对应的 update_Q_table 方法可以如下实现（这个实现没有完全按上面伪代码来，上面伪代码的意思是先收集到完整的一条 episode 后再进行价值更新，我这里则是完全 online 地，逐 transition 地进行价值更新）

class SarsaNStep(Slover):
    def __init__(self, env:gym.Env, n_step=5, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None):
        super().__init__(env, alpha, gamma, epsilon, seed)
        self.n_step = n_step    # 展开的步数
        self.state_list = []    # 保存之前的状态
        self.action_list = []   # 保存之前的动作
        self.reward_list = []   # 保存之前的奖励

    def update_Q_table(self, s, a, r, s_, a_, done):
        self.state_list.append(s)
        self.action_list.append(a)
        self.reward_list.append(r)

        # 保存的数据足够了，就进行 n step sarsa 更新
        if len(self.state_list) == self.n_step:
            # 计算后 n 步的收益作为 TD target
            G = self.Q_table[s_,a_]
            for i in reversed(range(self.n_step)):
                G = self.gamma * G + self.reward_list[i]    
            
            # 对list中第一个动作状态 pair 进行更新，然后将其从 list 移除 
            s = self.state_list.pop(0)  
            a = self.action_list.pop(0)
            self.reward_list.pop(0)
            self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])

        # 运行至此 list 中存储的轨迹长度一定小于 n
        # 如果本次 update 时 (s,a) 已经到达终止状态，list 中残余的动作状态 pair 无法往后看 n 步了，就能看多少看多少，也进行更新
        if done:
            G = self.Q_table[s_,a_]
            for i in reversed(range(len(self.state_list))):
                G = self.gamma * G + self.reward_list[i]    

                s = self.state_list[i]
                a = self.action_list[i]
                self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])

            # 即将开始下一条序列，将列表全清空
            self.state_list = []  
            self.action_list = [] 
            self.reward_list = []

正如我们在 2.1.2 节分析的，如果一个 value-based 方法在构造 TD target 时不依赖于当前策略 $\pi$ ，它就可以做为 off-policy 方法使用。标准 N-step Sarsa 方法用到了当前策略 $\pi$ ，因为当沿着轨迹展开时，被展开的轨迹是由当前策略 $\pi$ 和环境交互生成的，要想摆脱和 $\pi$ 的关系，可以把同样的这一条轨迹看做是由另一个目标策略生成的，然后用重要性采样比来保持 TD target 的期望不变。具体而言，现在把真正和环境交互的行为策略记作 $b$ ，要优化的目标策略记作 $\pi$ ，off-policy 形式下的 N-step Sarsa Bellman operator 迭代公式如下
$Q_\pi(S_t,A_t) \leftarrow Q_\pi(S_t,A_t) + \alpha \rho_{t:t+n-1}\big[G_{t:t+n} - Q_\pi(S_t,A_t) \big]$ 其中重要性采样比定义为
$\rho_{t:h} \doteq \prod_{k=t}^{\min(h,T-1)}\frac{\pi(A_k|S_k)}{b(A_k|S_k)}$ 如果让行为策略 $b$ 为 $\epsilon$ -greedy，目标策略 $\pi$ 为 greedy，引入重要度采样比后的 Off-policy N-step Sarsa 伪代码如下

对应的 update_Q_table 方法可以如下实现（这个实现没有完全按上面伪代码来，上面伪代码的意思是先收集到完整的一条 episode 后再进行价值更新，我这里则是完全 online 地，逐 transition 地进行价值更新）
```
class SarsaNStepOffpolicy(Slover):
    def __init__(self, env:gym.Env, n_step=5, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None):
        super().__init__(env, alpha, gamma, epsilon, seed)
        self.n_step = n_step    # 展开的步数
        self.state_list = []    # 保存之前的状态
        self.action_list = []   # 保存之前的动作
        self.reward_list = []   # 保存之前的奖励
        self.rho_list = []      # 保存每步 action 的重要度采样比

    def update_Q_table(self, s, a, r, s_, a_, done):
        self.state_list.append(s)
        self.action_list.append(a)
        self.reward_list.append(r)

        if a in self.greedy_policy[s]:
            p_target = 1.0/self.greedy_policy[s].shape[0]
            p_behavior = 1.0/self.greedy_policy[s].shape[0] + 1.0/self.n_action
            self.rho_list.append(p_target/p_behavior)
        else:
            self.rho_list.append(0)

        # 保存的数据足够了，就进行 n step sarsa 更新
        if len(self.state_list) == self.n_step:
            # 计算后 n 步的收益作为 TD target
            G = self.Q_table[s_,a_]
            rho = 1
            for i in reversed(range(self.n_step)):
                G = self.gamma * G + self.reward_list[i]    
                rho *= self.rho_list[i]
            
            # 对list中第一个动作状态 pair 进行更新，然后将其从 list 移除 
            s = self.state_list.pop(0)  
            a = self.action_list.pop(0)
            self.reward_list.pop(0)
            self.Q_table[s, a] += self.alpha * rho * (G - self.Q_table[s, a])

        # 运行至此 list 中存储的轨迹长度一定小于 n
        # 如果本次 update 时 (s,a) 已经到达终止状态，list 中残余的动作状态 pair 无法往后看 n 步了，就能看多少看多少，也进行更新
        if done:
            G = self.Q_table[s_,a_]
            rho = 1
            for i in reversed(range(len(self.state_list))):
                G = self.gamma * G + self.reward_list[i]    
                rho *= self.rho_list[i]

                s = self.state_list[i]
                a = self.action_list[i]
                self.Q_table[s, a] += self.alpha * rho * (G - self.Q_table[s, a])

            # 即将开始下一条序列，将列表全清空
            self.state_list = []  
            self.action_list = [] 
            self.reward_list = [] 
```

2.3.2 N-step Sarsa 实验

2.3.2.1 标准版本（On-policy 版本）

在 Cliff Walking 环境进行训练，学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$ 。价值收敛过程（三倍快放）和 return 收敛曲线如下（n 设置为 5）

注意收敛到了 Safer path，而且策略收敛之后发生了两次崩溃。接下来我们利用环境向量化技巧，让三个使用不用随机种子的 agent 在三个环境中并行交互训练，平均性能如下

注意到至少有一个 agent 发生了持续约 100 episode 的策略崩溃，这体现了 N-step Sarsa 的不稳定性
下面给出完整代码
1. 单 agent 训练带 UI 渲染：RL_task_practice/4/RL_SarsaNStep.py
2. 三 agent 并行训练无 UI： RL_task_practice/4/Performance_SarsaNStep.py

2.3.2.2 Off-policy 版本

在 Cliff Walking 环境进行训练，学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$ 。价值收敛过程（六倍快放）和 return 收敛曲线如下（n 设置为 5）

可见完全没有收敛，我认为这是因为轨迹中很容易出现 $\pi(a|s)=0$ 的 transition $(s, a, r, s^{'})$ ，导致大量样本被浪费了。如果一定要改成 off-policy，行为策略和目标策略必须仔细设计，尽量避免此问题
下面给出完整代码
1. 单 agent 训练带 UI 渲染：RL_task_practice/4/RL_SarsaNStepOffpolicy.py

2.4 N-step Tree Backup

2.4.1 N-step Tree Backup 原理

N-step Tree Backup 是一种不使用重要性采样比的 N-step 展开 off-policy 方法。N-step Tree Backup 是对 N-step Sarsa 的一个改进，上文我们分析了 Off-policy 版本 N-step Sarsa 不 work 原因在于：一旦某个 transition $(s, a, r, s^{'})$ 对应的目标策略 $\pi$ 有 $\pi(a|s)=0$ ，这整个 n 步展开的更新就无法进行，因为这时重要度采样比为 0 了，但事实上这个不可行的 transition 可能出现在展开的连续 n 步中间某个位置，其之前的部分还是可以进行计算的。N-step Tree Backup 进一步扩展了这个思想，之前我们介绍的方法中，TD target 都是由经过轨迹沿途的所有 reward（经过适当的折扣）和底部结点的价值估计组合而成的（如 2.1.3 节的回溯图），因此这个轨迹中的任意 transition 的重要度采样比为 0，都会使得整段轨迹的 TD target 计算为 0。在 N-step Tree Backup 中，TD target 除了以上成分，还要加上回溯图中每一层悬挂在两侧的动作结点的估计价值，这也是其名称的由来：价值更新源自于整个树的动作价值估计。下面给出 N-step Tree Backup 方法的回溯图

如左图所示，回溯图的骨干是行为策略 $b$ 交互采样到的真实轨迹，每一层的叶子是在状态下可行的其他动作对应的价值估计。右图红色线给出一个目标策略 $\pi$ 可能会选择的轨迹，可见 $\pi(A_{t+2} | S_{t+2}) =0$ ，这会导致 Off-policy N-step Sarsa 失败，而 N-step Tree Backup 仍可以更新
具体而言，我们可以把回溯树按照经历的状态划分阶段，最上面的称为第一阶段，这里目标策略 $\pi$ 的每个 $\neq A_{t+1}$ 的动作对 TD target 的贡献权重为 $\pi(a|S_{t+1})$ ，而 $\pi(A_{t+1}|S_{t+1})$ 用来给所有二级动作加权，以此类推
1. one-step Tree Backup 的 TD target 其实和 Expected Sarsa 完全一致，为
  $G_{t: t+1} \doteq R_{t+1}+\gamma \sum_{a} \pi\left(a \mid S_{t+1}\right) Q_{\pi}\left(S_{t+1}, a\right)$
2. two-step Tree Backup 的 TD target 为
  $\begin{aligned} G_{t: t+2} & \doteq R_{t+1}+\gamma \sum_{a \neq A_{t+1}} \pi\left(a \mid S_{t+1}\right) Q_\pi\left(S_{t+1}, a\right)+\gamma \pi\left(A_{t+1} \mid S_{t+1}\right)\left(R_{t+2}+\gamma \sum_{a} \pi\left(a \mid S_{t+2}\right) Q_\pi\left(S_{t+2}, a\right)\right) \\ & =R_{t+1}+\gamma \sum_{a \neq A_{t+1}} \pi\left(a \mid S_{t+1}\right) Q_\pi\left(S_{t+1}, a\right)+\gamma \pi\left(A_{t+1} \mid S_{t+1}\right) G_{t+1: t+2} \end{aligned}$
3. n-step Tree Backup 的 TD target 为
  $G_{t: t+n} \doteq R_{t+1}+\gamma \sum_{a \neq A_{t+1}} \pi\left(a \mid S_{t+1}\right) Q_{\pi}\left(S_{t+1}, a\right)+\gamma \pi\left(A_{t+1} \mid S_{t+1}\right) G_{t+1: t+n}$

下面给出 N-step Tree Backup 的伪代码
在这里插入图片描述
对应的 update_Q_table 方法可以如下实现（这个实现没有完全按上面伪代码来，上面伪代码的意思是先收集到完整的一条 episode 后再进行价值更新，我这里则是完全 online 地，逐 transition 地进行价值更新）

class NStepTreeBackup(Slover):
def __init__(self, env:gym.Env, n_step=5, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None):
    super().__init__(env, alpha, gamma, epsilon, seed)
    self.n_step = n_step    # 展开的步数
    self.state_list = []    # 保存之前的状态
    self.action_list = []   # 保存之前的动作
    self.reward_list = []   # 保存之前的奖励

def _greedy_action_probability(self, s, a):
    if a in self.greedy_policy[s]:
        return 1.0/self.greedy_policy[s].shape[0]
    else:
        return 0
        
def update_Q_table(self, s, a, r, s_, done):
    self.state_list.append(s)
    self.action_list.append(a)
    self.reward_list.append(r)

    # 保存的数据足够了，就进行 n 步树回溯
    if len(self.state_list) == self.n_step:
        # 展开计算 s_ 处期望 return 
        Q_exp = self.Q_table[s_].max()  # greedy 策略下的 E_a[Q(s_,a)]
        G = r + self.gamma * Q_exp

        # 沿着轨迹回溯并展开计算期望 return
        for i in reversed(range(self.n_step)):
            s, a, r = self.state_list[i], self.action_list[i], self.reward_list[i]
            leaf_value = 0
            for leaf_a in np.arange(self.n_action):
                if leaf_a != a:
                    leaf_value += self._greedy_action_probability(s, leaf_a) * self.Q_table[s,leaf_a]
            G = r + self.gamma * (leaf_value + self._greedy_action_probability(s, a) * G)   
        
        # 对list中第一个动作状态 pair 进行更新，然后将其从 list 移除 
        s = self.state_list.pop(0)  
        a = self.action_list.pop(0)
        self.reward_list.pop(0)
        self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])

    # 运行至此 list 中存储的轨迹长度一定小于 n
    # 如果本次 update 时 (s,a) 已经到达终止状态，list 中残余的动作状态 pair 无法往后看 n 步了，就能看多少看多少，也进行更新
    if done:      
        G = r
        for i in reversed(range(len(self.state_list))):
            s, a, r = self.state_list[i], self.action_list[i], self.reward_list[i]
            leaf_value = 0
            for leaf_a in np.arange(self.n_action):
                if leaf_a != a:
                    leaf_value += self._greedy_action_probability(s, leaf_a) * self.Q_table[s,leaf_a]
            G = r + self.gamma * (leaf_value + self._greedy_action_probability(s, a) * G)   

            s = self.state_list[i]
            a = self.action_list[i]
            self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])

        # 即将开始下一条序列，将列表全清空
        self.state_list = []  
        self.action_list = [] 
        self.reward_list = []

2.4.2 N-step Tree Backup 实验

在 Cliff Walking 环境进行训练，学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$ 。价值收敛过程（三倍快放）和 return 收敛曲线如下（n 设置为 5）

注意收敛到了 Safer path。接下来我们利用环境向量化技巧，让三个使用不用随机种子的 agent 在三个环境中并行交互训练，平均性能如下
下面给出完整代码
1. 单 agent 训练带 UI 渲染：RL_task_practice/4/RL_NStepTreeBackup.py
2. 三 agent 并行训练无 UI：RL_task_practice/4/Performance_NStepTreeBackup.py

2.5 Q-Learning

2.5.1 Q-Learning 原理

Q-Learning 是一种 Off-policy 方法，前面 2.2.1 节已经提到过，Q-Learning 就是一种目标策略为 greedy 策略的特殊的 Expected Sarsa 方法，因此它也和 Expected Sarsa 一样具有 “学习率不影响收敛结果” 和 “可以 Off-policy 使用” 的优点。具体而言，每轮迭代中，首先交互得到 transition 样本 $(s, a, r, s^{'})$ ，然后如下应用 Bellman optimal operator 评估最优价值
$Q_\pi(s.a) \leftarrow Q_\pi(s,a) + \alpha\big[r + \gamma \max_{a'} Q_\pi(s',a')-Q_\pi(s,a)\big]$ 接下来直接做贪心来更新目标策略 $\pi$ ，再增加 $\epsilon$ 探索就得到行为策略 $b$ 。从公式上看 Q-Learning 更像价值迭代，它用 Bellman optimal operator 直接估计最优价值函数 $Q^*$ ，不像 Sarsa 那样有比较明显的 GPI 过程

下面给出 Q-Learning 的伪代码
在这里插入图片描述

对应的 update_Q_table 方法可以如下实现

class QLearning(Slover):
    def __init__(self, env:gym.Env, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None):
        super().__init__(env, alpha, gamma, epsilon, seed)
    
    def update_Q_table(self, s, a, r, s_, batch_size=0):
        if batch_size == 0: # on-policy
            td_target = r + self.gamma * self.Q_table[s_].max()
            td_error = td_target - self.Q_table[s,a]
            self.Q_table[s,a] += self.alpha * td_error
        else:               # off-policy
            self.replay_buffer.push_transition(transition=(s, a, r, s_))
            transitions = self.replay_buffer.sample_batch(batch_size)
            for s, a, r, s_ in transitions:
                td_target = r + self.gamma * self.Q_table[s_].max()
                td_error = td_target - self.Q_table[s,a]
                self.Q_table[s,a] += self.alpha * td_error
        self.policy_is_updated = False

2.5.2 Q-Learning 实验

2.5.2.1 标准版本

在 Cliff Walking 环境进行训练，学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$ 。价值收敛过程（三倍快放）和 return 收敛曲线如下

注意收敛到了 Optimal path。接下来我们利用环境向量化技巧，让三个使用不用随机种子的 agent 在三个环境中并行交互训练，平均性能如下

2.5.2.2 提高学习率

由于前面分析了 Q-Learning 的收敛不受学习率影响，下面把学习率改为 $\alpha=1$ 再重复上述实验，结果如下

可见收敛速度大大提升了，这意味着样本效率显著提升

2.5.2.3 使用 replay buffer

前面分析了可以 Off-policy 使用，下面利用 replay buffer 每次迭代随机采样 5 个 transition 重复上述实验，结果如下

可见收敛速度大大提升了，这意味着样本效率显著提升
下面给出完整代码
1. 单 agent 训练带 UI 渲染：RL_task_practice/4/RL_QLearning.py
2. 三 agent 并行训练无 UI： RL_task_practice/4/Performance_QLearning.py

2.6 Double Q-Learning

2.6.1 Double Q-Learning 原理

Double Q-Learning 是一种 Off-policy 方法。很多 TD control 算法都包含 “最大化操作”，比如 value-based 类方法中 Bellman optimal equation 中的 max 运算，或者 Actor-Critic 类方法中 Actor 的梯度运算（可参考TD3论文），这种最大化操作会导致 agent 高估价值。具体而言，在估计值的基础上进行最大化操作也可以被看作隐式地对最大值进行估计，这会带来一个显著的正偏差。例如，假设状态 $s$ 下可以选择多个动作 $a$ ，所有二元组 $(s, a)$ 的真实价值 $Q (s, a)$ 都为 0。在估计状态动作价值时，估计值 $Q (s, a)$ 是不确定的，可能大于0也可能小于0，但由于我们的最大化操作，往往会选出偏大的估计，这就产生了正偏差。
- 考虑下图所示的简单MDP。这个MDP有A和B两个非终止节点。每幕从 A 开始并随机向左或右前进。如图所示，以向右开始的轨迹 return 为0；以向左开始的轨迹 return 服从均值-0.1方差1.0的正态分布。 可见从A开始向左的收益均值为 -0.1，而向右是 0，所以我们的策略应该完全不选择向左
  使用Q-learning算法进行学习，行动策略使用 $\epsilon$ -贪心，设置 $\epsilon=0.1,\alpha = 0.1,\gamma = 1$ 。结果如折线图红线所示，Q-learning在开始阶段选择向左的概率远高于向右，且向左的概率会一直显著地高于5%（5% 是使用 $\epsilon=0.1$ 的概率随机试探引起的最低的向左运动概率）
造成这个问题的本质是确定价值最大的动作和估计价值这两个过程使用了相同的样本（多幕序列）。分析上述例子，用 Q-learning 的 Q 函数更新公式计算 $Q (A, 向左)$ 时，带入参数值有
$\leftarrow Q(A,向左) + 0.1\times\big[0 +1\times \max_aQ(B,a)-Q(A,向左)\big]$ 我们拆开分析这个过程
1. 确定价值最大动作：每轮更新时， $\max_a Q(B,a),a \in \mathcal{N}(-0.1,1)$ 这个操作，会使B到左边终态的每一个可能路线进行一次 $\mathcal{N}(-0.1,1)$ 上的采样作为奖励，一旦某个采样结果为正奖赏，这里的最大化操作就会选出一个具有正价值的二元组 $(B, a)$
2. 估计价值：直接使用 $max_a Q(B,a)$ 估计 $Q (A, 向左)$ 时，最大化操作得到的早期正价值进一步转移到 $Q (A, 向左)$ 上，使得学习过程初期倾向于选择向左。
3. 随着学习过程进行，确定价值最大动作时大量的正态分布采样给出大量负价值的 $(B, a)$ ，逐渐修正 $Q (A, 向左)$ 为负，选择向左走的概率随之降低。
双学习可以有效解决最大化偏差问题，折线图绿线给出了 Double Q-Leaning 的动作情况，完全没有出现上述问题。注意到问题的本质在于：最大化操作选出的动作 $a$ ，其状态动作价值 $Q(S_{t+1},a)$ 是真实状态动作价值的一个偏大估计，又由于确定价值最大的动作和估计价值这两个过程使用了相同的样本（多幕序列），导致依赖 $Q(S_{t+1},a)$ 进行计算的 $Q(S_t,A_t)$ 也成为有偏估计。由于最大化操作带来的估计偏差是不可避免的，想要得到无偏的 $Q$ 函数，只能考虑防止估计偏差从 $Q(S_{t+1},a)$ 传递到 $Q(S_t,A_t)$ 。Double Q-Learning 如下实现这个思路
1. 将样本分为两个集合，分别学习两个独立的价值估计 $Q_1(S,A)$ 和 $Q_2(S,A)$
2. 对于 transition $(s, a, r, s^{'})$ 构造 Q-Learning 的 TD target 时，使用其中一个估计 $Q_1(a)$ 来确定最优动作 $A^* = \argmax_AQ_1(s, A)$ 再用另一个 $Q_2$ 来得到价值的估计 $Q_2(s, A^*)$ 根据 $Q$ 函数的定义， $Q_1(s,\argmax_aQ_2(s,a))$ 这个估计是无偏的。同理还可以得到另一个无偏估计 $Q_1(s,\argmax_aQ_2(s,a))$ 。虽然这里一共学习了两个估计值，但是对每个样本集合只更新一个估计值。双Q学习需要双倍的内存，但每步无需额外的计算量
3. 双学习的思想可以自然地推广到那些为完备MDP设计的算法中，例如双Q学习、双sarsa学习、双期望sarsa学习等。以双Q学习为例，对于任意 transition $(s, a, r, s^{'})$ ，以一半一半的概率执行以下两个更新
  $Q_1(s,a) \leftarrow Q_1(s,a) + \alpha\big[r+\gamma Q_2(s',\argmax_aQ_1(s',a))-Q_1(s,a) \big] \\ Q_2(s,a) \leftarrow Q_2(s,a) + \alpha\big[r+\gamma Q_1(s',\argmax_aQ_2(s',a))-Q_2(s,a) \big] \\$
4. 双学习中两个近似函数的地位是完全相同的，两种动作价值的估计值都可以在行为策略中使用。比如双 Q 学习的行为策略可以基于两个 Q 函数的均值或和进行 $\epsilon$ -贪心

下面给出 Q-Learning 的伪代码
在这里插入图片描述
对应的 update_Q_table 方法可以如下实现

class QLearningDouble(Slover):
    def __init__(self, env:gym.Env, alpha=0.1, gamma=0.9, epsilon=0.1, seed=None):
        super().__init__(env, alpha, gamma, epsilon, seed)
        self.Q_table_ = self.Q_table.copy()

    def update_V_table(self):
        if not self.policy_is_updated:
            self.update_policy()

        for i in range(self.n_observation):
            Q_mean = 0.5*(self.Q_table_ + self.Q_table)
            greedy_actions = self.greedy_policy[i]
            self.V_table[i] = Q_mean[i][greedy_actions[0]]    # 贪心策略有 v(s) = E_a[Q(s,a)|s] = max_a Q(s,a|s)

    def update_policy(self):
        Q_sum = self.Q_table_ + self.Q_table
        best_action_value = np.max(Q_sum, axis=1)
        # 返回一个 ndarray 组成的列表，每个 ndarray 由对应状态下最优动作组成
        self.greedy_policy = np.array([np.argwhere(Q_sum[i]==best_action_value[i]).flatten() for i in range(self.n_observation)], dtype=object)
        self.policy_is_updated = True

    def update_Q_table(self, s, a, r, s_, batch_size=0):
        transitions = [(s, a, r, s_)]
        if batch_size > 0:
            self.replay_buffer.push_transition(transition=(s, a, r, s_))
            transitions = self.replay_buffer.sample_batch(batch_size)
        for s, a, r, s_ in transitions:
            if self.rng.random() < 0.5:
                td_target = r + self.gamma * self.Q_table[s_][np.argmax(self.Q_table_[s_])]
                td_error = td_target - self.Q_table_[s,a]
                self.Q_table_[s,a] += self.alpha * td_error
            else:
                td_target = r + self.gamma * self.Q_table_[s_][np.argmax(self.Q_table[s_])]
                td_error = td_target - self.Q_table[s,a]
                self.Q_table[s,a] += self.alpha * td_error       
        self.policy_is_updated = False

2.6.2 Double Q-Learning 实验

2.6.2.1 标准设定

在 Cliff Walking 环境进行训练，学习率 $\alpha=0.1$ ，探索概率 $\epsilon=0.1$ ，折扣系数 $\gamma=0.9$ 。价值收敛过程（六倍快放）和 return 收敛曲线如下

注意收敛到了 Safer path。接下来我们利用环境向量化技巧，让三个使用不用随机种子的 agent 在三个环境中并行交互训练，平均性能如下

由于 Double Q-Learning 需要把两个 Q 表都估计好才能较好地收敛，所以这里使用的轨迹数量翻倍到 1400 条了。虽然 Double Q-Learning 可以缓解价值高估问题，但也导致样本效率下降，收敛更慢

2.6.2.2 使用 replay buffer

前面分析了可以 Off-policy 使用，下面利用 replay buffer 每次迭代随机采样 5 个 transition 重复上述实验，结果如下

可见收敛速度大大提升了，这意味着样本效率显著提升。另外收敛轨迹变成了 optimal path
下面给出完整代码
1. 单 agent 训练带 UI 渲染：RL_task_practice/4/RL_QLearningDouble.py
2. 三 agent 并行训练无 UI： RL_task_practice/4/Performance_QLearningDouble.py

3. 总结

下面的表格简略地总结了各种方法的特点（注：off-policy 策略均可以 on-policy 地使用）

方法	策略性质	算子	轨迹展开步数	收敛	学习率	备注
Sarsa	on-policy	Bellman operator	1	Safer path	影响收敛结果	-
Expected Sarsa	off-policy	Bellman operator	1	Safer path	不影响收敛结果	-
N-step Sarsa	on-policy	Bellman operator	N	Safer path	影响收敛结果	可转 off-policy
N-step Tree Backup	off-policy	Bellman operator	N	Safer path	影响收敛结果	-
Q-Learning	off-policy	Bellman optimal operator	1	optimal path	不影响收敛结果	-
Double Q-Learning	off-policy	Bellman optimal operator	1	Safer path	影响收敛结果	要估计两个 Q 表，慢

3.1 性能对比

前面所有并行测试时，我都把得到的 return 曲线（ndarray）保存为 .npy 文件，然后就可以用下面的代码同时加载多条曲线来对比不用方法的性能

import matplotlib.pyplot as plt
import numpy as np

colors = ['r', 'b', 'c', 'g', 'k', 'y', 'm']
#algorithms = ['QLearning', 'QLearning_alpha=1', 'QLearning_replay=5', 'Sarsa', 'Sarsa_alpha=1']
#algorithms = ['QLearning', 'QLearning_alpha=1', 'QLearning_replay=5']
#algorithms = ['SarsaExp', 'SarsaExp_alpha=1', 'QLearning', 'QLearning_alpha=1', 'QLearning_replay=5' ]
algorithms = ['SarsaExp', 'Sarsa',]
#algorithms = ['SarsaExp', '5StepTreeBackup', 'Sarsa5Step']

plt.xlabel('Episodes')
plt.ylabel('Ave Returns')
plt.title('TD methods on {}'.format('Cliff Walking'))

for algo, color in zip(algorithms, colors):
    envs_returns = np.load(f'data/{algo}'+'.npy')
    num_episodes = envs_returns.shape[1]

    ave_performance = envs_returns.mean(axis=0)                                         # 多个随机种子实验的平均性能
    filter_length = int(num_episodes/20)                                                # 滑动均值滤波长度
    ave_sliding = np.convolve(ave_performance, np.ones(filter_length)/filter_length, mode='valid')  # 一维卷积实现滑动均值滤波
    x = np.arange(0.5*filter_length,0.5*filter_length + ave_sliding.shape[0])           # 滤波后数据，显示时跳过数据不完全重叠的边际部分

    plt.plot(np.arange(envs_returns.shape[1]), ave_performance, c=color, alpha=0.2)   # 原始数据半透明显示
    plt.plot(x, ave_sliding, alpha=0.8, c=color, label=algo)                                      # 滤波后数据实现显示

plt.legend()
plt.show()

下面展示一些结果并进行分析
1. 各种 Q-Learning 和 Sarsa 的对比。可见 Q-Learning 虽然能收敛到 optimal path，但是这条轨迹容错率太低，增加随机探索后的行为策略性能反而不如收敛到 safer path 的 Sarsa 方法。另外提高学习率和使用经验重放都能加快 Q-Learning 的收敛，Sarsa 则不能用这些技巧
2. 这个简单的环境中，标准 Expected Sarsa 和 Sarsa 性能差不多
3. Expected Sarsa 作为 off-policy 可以用经验重放，还能使用更高的学习率，性能最好
4. 虽然 Double Q-Learning 需要收敛的时间更长，但是它收敛到了对行为策略更合适的 safer path；通过经验重放可以大幅提高收敛速度，但是收敛结果变成了风险更高的 optimal path，这里的原因我还有点没想明白
5. 多步展开可以提高样本利用率加速收敛，N-step Tree Backup 比 N-step Sarsa 更稳定
6. 所有结果数据可以从此处获取，结合上面的绘图代码可以进行更多比较分析

3.2 总结

经验重放、多步展开、提高学习率都是提高样本效率的有效措施，但需要注意所选方法是否支持这些技巧
1. 一个 value-based 方法能不能用作 off-policy 方法（从而支持经验回放），关键是看我们为目标策略 $\pi$ 构造 TD target 时有没有用到行为策略 $b$ ，如果用到了，那就意味着训练用的数据必须来自收集数据的策略，这样就无法重用过去较差策略收集的数据
2. 沿着轨迹多步展开可以提高样本利用效率，因为这样处理后有机会在一条轨迹上做更多次价值更新，比如下例
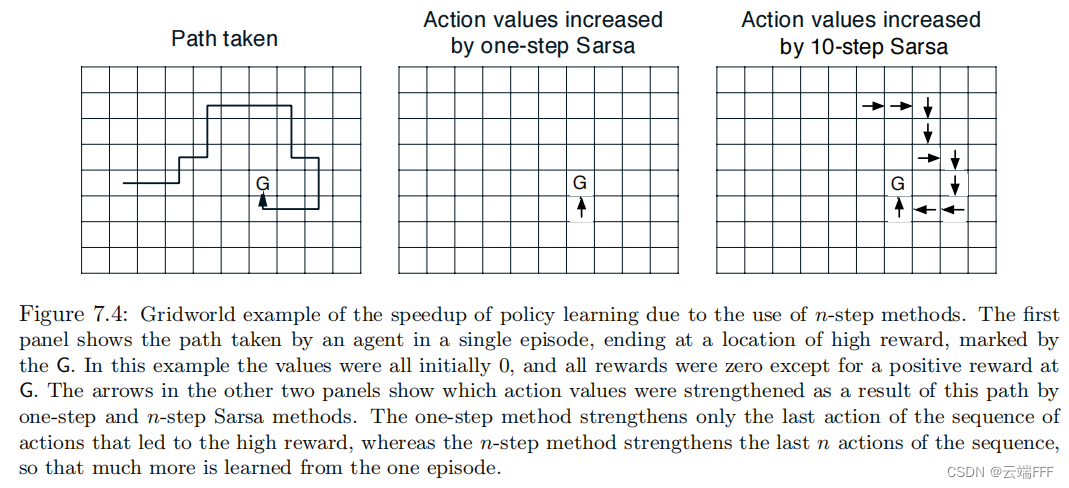
3. 只有少数特殊情况下学习率与收敛结果无关，虽然提高学习率是加速收敛的最高效手段，但能否用这一招需要仔细分析
Sarsa 类方法收敛到了 safer path，而 Q-Learning 收敛到 optimal path，这可以从两个角度理解
1. 这类方法往前多看了一步 action，因此由于随机性而落下悬崖的情况被考虑到，使得这些位置价值下降；
2. Sarsa 等 on-policy 方法直接就是针对 $\epsilon$ -greedy 策略而优化的，因此收敛结果和静态的 optimal policy 有区别
虽然在本次实验中没有测试，但只要让 $\epsilon$ 逐渐减小到 0，则这些方法都能收敛到 optimal path。