[1] Li W, Gao S, Li X, et al. TCP-NeuRoc: Neural Adaptive TCP Congestion Control with Online Changepoint Detection[J]. IEEE Journal on Selected Areas in Communications, 2021.
NeuRoc (shorten for NeuRal adaptive with online changepoint detection)
NeuRoc采用在线变点检测和神经网络框架实现“冷启动(cold-start)”和快速推理。它采用强化学习的方法预测BDP并采取相应的行动调整拥塞窗口大小,以达到高吞吐量、低延迟的目的。
冷启动: 根据BBR初始化其CC规则,并采用概率方法探索执行过程中的随机动作。
1. 脉络
- Section 2:研究动机和解决方案概述
- Section 3:介绍基于在线变点检测的深度神经自适应TCP拥塞控制的详细机制
- Section 4:讨论本文提出的基于学习的TCP拥塞控制的实现和部署问题
- Section 5:评估系统的性能
- Section 6:总结该领域的相关工作
- Section 7:讨论基于学习的机制的局限性和未来的工作
2. Motivation及解决方案概述
2.1 启发式的问题
测试采用的网络状况
- 随机丢包率0.1%
- 延迟20ms
- 可用带宽在40 Mbps到80 Mbps之间波动
测试结果

- Vegas和Cubic无法充分利用可用带宽。
- 当可用带宽发生变化时,Vivace和BBR都能自适应地调整其发送速率。Vivace的反应比BBR慢,且发送速率与带宽之间存在差距。BBR为了使网络带宽利用率最大化,倾向于发送比可用带宽更多的数据。
- 由于BBR在发送速率方面更加积极,它比其他算法占用了更多的缓冲区。虽然它的吞吐量几乎与可用带宽相同,但它导致的延迟和抖动明显高于其他算法。
总结
现有的CC算法要么在动态网络中缺乏适应性,要么妥协于一至多个性能维度。
2.2 强化学习的问题
- 探索各种行动耗费大量时间,形成预训练模型的时间长。
- 每次训练的模型成本很高,决策的延迟时间也很长
2.3 优化目标
最大化功率函数 p o w e r ( G ) = G B ( G ) power(G)=\frac{G}{B(G)} power(G)=B(G)G??? ,其中 G G G? 为平均吞吐量, B ( G ) B(G) B(G)?? 为平均响应时间。
由此引出 B D P = B t l B w × R T p r o p B D P=B t l B w \times R T p r o p BDP=BtlBw×RTprop
最优的TCP工作点对应于用等于BDP的数据量填充管道,这样可以在不引入排队延迟(保持缓冲区接近空)的情况下充分利用带宽。
2.4 解决方法概述
考虑现有算法的缺陷以及期望达到的目标,作者提出了一个称为TCP-NeuRoc的基于学习的解决方案,以优化TCP拥塞控制。它采用深度强化学习方法,在近似BDP和探索窗口调整策略的基础上生成拥塞控制策略,可以在动态网络环境中逐步接近系统的最佳运行点。
3. 详细机制
3.1 整体框架及流程

该方法运行于接收端,分别由变点检测模块和强化学习agent两部分组成。
变点检测器持续追踪发送的包和对应返回的ACK,以形成网络性能指标的序列(包含包延迟、丢包率…)。然后根据该序列判断网络情况是否有重大变化(如可用带宽、延迟的增加/减少等)。
- 如果没有发生变化,应用当前的CC Rule确定cwnd
- 如果发生变化,新观察到的网络状态将触发agent,agent根据状态采取行动,同时观察环境中的奖励,并相应地更新CC Rule。
强化学习agent的目标是生成最优的CC Rule。
3.2 Monitor Interval(MI)
在每个MI开始时,发送方决定调整其CC Rule,以控制数据发送速率。
采取可变的MI,MI的最大长度限制为T毫秒。一般的T设为200ms,大约是4~5个RTTs。在每个MI中,系统通过观察一段时间内的一些性能指标,不断跟踪网络情况。**变点被定义为观察到的时间序列数据的突然变化。**在我们的系统中,每个MI最多持续T毫秒。==如果检测到一个变点,MI将在小于T的时间内提前结束。==下图中红点为变点,出现变点的位置MI明显偏小。值得注意的是,变点本身不代表MI的边界,因为它往往需要几个额外的样本来检测突然的变化。

3.3 在线变点检测器
变点检测器的工作原理是检查序列中是否存在概率特征明显不同的区域。
公式推导
使用
d
1
,
d
2
,
?
?
,
d
i
,
?
d_{1}, d_{2}, \cdots, d_{i}, \cdots
d1?,d2?,?,di?,?? 表示输入样本,用
d
i
:
j
=
{
d
i
,
?
?
,
d
j
}
\mathbf{d}_{i: j}=\left\{d_{i}, \cdots, d_{j}\right\}
di:j?={di?,?,dj?}?? 表示介于第
i
i
i? 次和第
j
j
j?? 次观察之间的连续样点。将
r
u
n
?
l
e
n
g
t
h
run\ length
run?length? 定义为上一次变点出现后累计的样本数。定义
L
i
\mathcal{L}_{i}
Li?? 为第
i
i
i? 个样本的
r
u
n
?
l
e
n
g
t
h
run\ length
run?length??
L
i
=
{
0
,
?if?
d
i
?is?a?changepoint?or?
i
=
1
L
i
?
1
+
1
,
?otherwise?
\mathcal{L}_{i}= \begin{cases}0, & \text { if } d_{i} \text { is a changepoint or } \mathrm{i}=1 \\ \mathcal{L}_{i-1}+1, & \text { otherwise }\end{cases}
Li?={0,Li?1?+1,??if?di??is?a?changepoint?or?i=1?otherwise??
如果
L
i
=
ω
\mathcal{L}_{i}=\omega
Li?=ω ,则可推测
L
i
?
ω
=
0
\mathcal{L}_{i-\omega}=0
Li?ω?=0 ,说明变点位于
d
i
?
ω
{d}_{i-\omega}
di?ω? 中。因此,
d
i
?
ω
{d}_{i-\omega}
di?ω? 是变点的后验概率为
P
(
L
i
=
ω
∣
d
1
:
i
)
P\left(\mathcal{L}_{i}=\omega \mid \mathbf{d}_{1: i}\right)
P(Li?=ω∣d1:i?) ,由此导出变点检测的条件:
P
(
L
i
=
ω
∣
d
1
:
i
)
>
η
P\left(\mathcal{L}_{i}=\omega \mid \mathbf{d}_{1: i}\right)>\eta
P(Li?=ω∣d1:i?)>η
其中,
η
∈
[
0
,
1
]
\eta \in[0,1]
η∈[0,1]? 是一个预先设定的概率阈值。依据贝叶斯定理,有
P
(
L
i
∣
d
1
:
i
)
=
P
(
L
i
,
d
1
:
i
)
P
(
d
1
:
i
)
=
P
(
L
i
,
d
1
:
i
)
Σ
L
i
P
(
L
i
,
d
1
:
i
)
P\left(\mathcal{L}_{i} \mid \mathbf{d}_{1: i}\right)=\frac{P\left(\mathcal{L}_{i}, \mathbf{d}_{1: i}\right)}{P\left(\mathbf{d}_{1: i}\right)}=\frac{P\left(\mathcal{L}_{i}, \mathbf{d}_{1: i}\right)}{\Sigma_{\mathcal{L}_{i}} P\left(\mathcal{L}_{i}, \mathbf{d}_{1: i}\right)}
P(Li?∣d1:i?)=P(d1:i?)P(Li?,d1:i?)?=ΣLi??P(Li?,d1:i?)P(Li?,d1:i?)?
其中,联合概率分布
P
(
L
i
,
d
1
:
i
)
P\left(\mathcal{L}_{i}, \mathbf{d}_{1: i}\right)
P(Li?,d1:i?) 可被计算为
P
(
L
i
,
d
1
:
i
)
=
Σ
L
i
?
1
P
(
L
i
,
L
i
?
1
,
d
1
:
i
)
=
Σ
L
i
?
1
P
(
L
i
,
d
i
∣
L
i
?
1
,
d
1
:
i
?
1
)
P
(
L
i
?
1
,
d
1
:
i
?
1
)
=
Σ
L
i
?
1
P
(
L
i
∣
L
i
?
1
)
P
(
d
i
∣
d
1
:
i
?
1
)
P
(
L
i
?
1
,
d
1
:
i
?
1
)
\begin{aligned} &P\left(\mathcal{L}_{i}, \mathbf{d}_{1: i}\right) \\ &=\Sigma_{\mathcal{L}_{i-1}} P\left(\mathcal{L}_{i}, \mathcal{L}_{i-1}, \mathbf{d}_{1: i}\right) \\ &=\Sigma_{\mathcal{L}_{i-1}} P\left(\mathcal{L}_{i}, d_{i} \mid \mathcal{L}_{i-1}, \mathbf{d}_{1: i-1}\right) P\left(\mathcal{L}_{i-1}, \mathbf{d}_{1: i-1}\right) \\ &=\Sigma_{\mathcal{L}_{i-1}} P\left(\mathcal{L}_{i} \mid \mathcal{L}_{i-1}\right) P\left(d_{i} \mid \mathbf{d}_{1: i-1}\right) P\left(\mathcal{L}_{i-1}, \mathbf{d}_{1: i-1}\right) \end{aligned}
?P(Li?,d1:i?)=ΣLi?1??P(Li?,Li?1?,d1:i?)=ΣLi?1??P(Li?,di?∣Li?1?,d1:i?1?)P(Li?1?,d1:i?1?)=ΣLi?1??P(Li?∣Li?1?)P(di?∣d1:i?1?)P(Li?1?,d1:i?1?)?
第一项
P
(
L
i
∣
L
i
?
1
)
P\left(\mathcal{L}_{i} \mid \mathcal{L}_{i-1}\right)
P(Li?∣Li?1?) 是运行长度的条件先验。它只有两种可能:运行长度继续增长,
L
i
=
L
i
?
1
+
1
\mathcal{L}_{i}=\mathcal{L}_{i-1}+1
Li?=Li?1?+1,或者出现变化点,
L
i
=
0
\mathcal{L}_{i}=0
Li?=0 。假设在样本序列中发现变化点的先验概率是
?
\epsilon
? ,可得:
P
(
L
i
∣
L
i
?
1
)
=
{
1
?
?
,
?if?
L
i
=
L
i
?
1
+
1
?
,
?if?
L
i
=
0
0.
?else?
P\left(\mathcal{L}_{i} \mid \mathcal{L}_{i-1}\right)= \begin{cases}1-\epsilon, & \text { if } \mathcal{L}_{i}=\mathcal{L}_{i-1}+1 \\ \epsilon, & \text { if } \mathcal{L}_{i}=0 \\ 0 . & \text { else }\end{cases}
P(Li?∣Li?1?)=??????1??,?,0.??if?Li?=Li?1?+1?if?Li?=0?else??
第二项
P
(
d
i
∣
d
1
:
i
?
1
)
P\left(d_{i} \mid \mathbf{d}_{1: i-1}\right)
P(di?∣d1:i?1?)? 是在已知
d
1
:
i
?
1
\mathbf{d}_{1: i-1}
d1:i?1?? 的情况下,最新观察到的样本是
d
i
d_{i}
di???? 的后验概率。根据贝叶斯定理可得
P
(
d
i
∣
d
1
:
i
?
1
)
=
∫
?
P
(
d
i
∣
?
)
P
(
?
∣
d
1
:
i
?
1
)
d
?
=
∫
?
P
(
d
i
∣
?
)
P
(
d
1
:
i
?
1
∣
?
)
P
(
?
)
P
(
d
1
:
i
?
1
)
d
?
\begin{aligned} P\left(d_{i} \mid \mathbf{d}_{1: i-1}\right) &=\int_{\vartheta} P\left(d_{i} \mid \vartheta\right) P\left(\vartheta \mid \mathbf{d}_{1: i-1}\right) \mathrm{d} \vartheta \\ &=\int_{\vartheta} P\left(d_{i} \mid \vartheta\right) \frac{P\left(\mathbf{d}_{1: i-1} \mid \vartheta\right) P(\vartheta)}{P\left(\mathbf{d}_{1: i-1}\right)} \mathrm{d} \vartheta \end{aligned}
P(di?∣d1:i?1?)?=∫??P(di?∣?)P(?∣d1:i?1?)d?=∫??P(di?∣?)P(d1:i?1?)P(d1:i?1?∣?)P(?)?d??
其中超参数
?
\vartheta
? 代表样本真实分布模型的参数。通常情况下,由于
?
\vartheta
? 是不确定的,因此这一积分难以计算。根据共轭贝叶斯分析法,可以利用 根据共轭贝叶斯分析法,我们可以利用
P
(
?
)
P(\vartheta)
P(?) 的共轭先验分布,得出一个接近的表达形式
P
(
?
)
P(\vartheta)
P(?) 的共轭先验分布,得出一个接近的表达形式。如果样本
d
i
d{i}
di 来自正态分布
N
(
d
,
σ
2
)
N\left(d, \sigma^{2}\right)
N(d,σ2) ,具有未知的均值
d
d
d 和标准差
σ
\sigma
σ ,那么它的共轭先验分布是具有四个超参数
μ
,
v
,
α
,
β
\mu, v, \alpha, \beta
μ,v,α,β? 的正态-逆伽马分布,即
(
d
,
σ
2
)
~
N
?
Γ
?
1
(
μ
,
v
,
α
,
β
)
\left(d, \sigma^{2}\right) \sim \mathrm{N}-\Gamma^{-1}(\mu, v, \alpha, \beta)
(d,σ2)~N?Γ?1(μ,v,α,β)
这些超参数可以以迭代的方式计算出来:
{
μ
(
i
)
=
v
(
i
?
1
)
μ
(
i
?
1
)
+
d
i
v
(
i
?
1
)
+
1
v
(
i
)
=
v
(
i
?
1
)
+
1
α
(
i
)
=
α
(
i
?
1
)
+
1
2
β
(
i
)
=
β
(
i
?
1
)
+
v
(
i
?
1
)
1
+
v
(
i
?
1
)
(
d
i
?
μ
(
i
?
1
)
)
2
2
\left\{\begin{array}{l} \mu^{(i)}=\frac{v^{(i-1)} \mu^{(i-1)}+d_{i}}{v^{(i-1)}+1} \\ v^{(i)}=v^{(i-1)}+1 \\ \alpha^{(i)}=\alpha^{(i-1)}+\frac{1}{2} \\ \beta^{(i)}=\beta^{(i-1)}+\frac{v^{(i-1)}}{1+v^{(i-1)}} \frac{\left(d_{i}-\mu^{(i-1)}\right)^{2}}{2} \end{array}\right.
??????????μ(i)=v(i?1)+1v(i?1)μ(i?1)+di??v(i)=v(i?1)+1α(i)=α(i?1)+21?β(i)=β(i?1)+1+v(i?1)v(i?1)?2(di??μ(i?1))2??
其中,
μ
(
i
)
,
v
(
i
)
,
α
(
i
)
\mu^{(i)}, v^{(i)}, \alpha^{(i)}
μ(i),v(i),α(i),
β
(
i
)
\beta^{(i)}
β(i) 是基于观测值
d
i
d{i}
di 的第
i
i
i 次超参数更新。有了估计的超参数,
P
(
d
i
∣
d
1
:
i
?
1
)
P\left(d_{i} \mid \mathbf{d}_{1: i-1}\right)
P(di?∣d1:i?1?) 可被估计为
P
(
d
i
∣
d
1
:
i
?
1
)
=
T
2
α
(
d
i
∣
μ
,
β
(
v
+
1
)
v
α
)
P\left(d_{i} \mid \mathbf{d}_{1: i-1}\right)=T_{2 \alpha}\left(d_{i} \mid \mu, \frac{\beta(v+1)}{v \alpha}\right)
P(di?∣d1:i?1?)=T2α?(di?∣μ,vαβ(v+1)?)
第三项与等式左边类似,采用迭代的方法计算。
算法实现

变化点检测形成了一个灵活的MI分区,这些分区被进一步用来形成机器学习的状态表示。
3.4 强化学习
DDPG + Actor-Critic

Agent
每当MI启动时,agent就会被触发,生成调整拥塞窗口大小的策略。
State
o t = ( R T T t  ̄ , Δ R T T t , ?Thrput? t  ̄ , Δ ?Thrput? t , S R t , L R t ) o_{t}=\left(\overline{R T T_{t}}, \Delta R T T_{t}, \overline{\text { Thrput }_{t}}, \Delta \text { Thrput }_{t}, S R_{t}, L R_{t}\right) ot?=(RTTt??,ΔRTTt?,?Thrput?t??,Δ?Thrput?t?,SRt?,LRt?)
| 特征 | 意义 |
|---|---|
| R T T t  ̄ \overline{R T T_{t}} RTTt?? | 包的平均往返时延 |
| Δ R T T t \Delta R T T_{t} ΔRTTt? | 包往返时延的方差 |
| ?Thrput? t  ̄ \overline{\text { Thrput }_{t}} ?Thrput?t?? | 平均吞吐量 |
| Δ ?Thrput? t \Delta \text { Thrput }_{t} Δ?Thrput?t? | 吞吐量的方差 |
| S R t S R_{t} SRt? | 在第t次MI中,确认的包与发送的包的比例 |
| L R t L R_{t} LRt? | 平均RTT与MI中观察到的最小RTT之比 |
了充分考虑动态网络情况的趋势,代理考虑最新的k个统计向量进行决策。最终用作agent输入的状态表示为
s
t
=
(
o
t
?
k
?
1
,
…
,
o
t
?
1
)
s_{t}=\left(o_{t-k-1}, \ldots, o_{t-1}\right)
st?=(ot?k?1?,…,ot?1?)
Action
与BBR的目标类似,优化的目标是使系统在最佳工作点上运行,其中理想的拥塞窗口大小应该等于BDP。因此,将action(即CC规则)定义为
?cwnd?
=
a
t
?
Thrput
?
max
?
?
R
T
T
m
i
n
\text { cwnd }=a_{t} * \operatorname{Thrput}_{\max } * R T T_{m i n}
?cwnd?=at??Thrputmax??RTTmin?
其中,
Thrput
?
max
?
\operatorname{Thrput}_{\max }
Thrputmax? 和
R
T
T
m
i
n
R T T_{m i n}
RTTmin? 是一个MI内观察到的最大吞吐量和最小RTT。
a
t
∈
(
0
,
2
)
a_{t} \in(0,2)
at?∈(0,2) 是增益系数,用于控制窗口大小。从理论上讲,TCP CC的最佳工作点对应于稳定状态下的
a
t
a_{t}
at?=1。而在实践过程中,
Thrput
?
max
?
\operatorname{Thrput}_{\max }
Thrputmax? 和
R
T
T
m
i
n
R T T_{m i n}
RTTmin? 往往会偏离真实值,因此需要搜索得到一个合适的增益系数
a
t
a_{t}
at??对窗口大小进行调整。如果当前发送速率导致观察到的性能指标下降,则将a降低到1以下,反之亦然。
Policy
详见下一节
Reward
R ( s t , a t ) = w t V t T h r p u t ? w d V t R T T ? w j V t J i t t e r R\left(s_{t}, a_{t}\right)=w_{t} V_{t}^{T h r p u t}-w_{d} V_{t}^{R T T}-w_{j} V_{t}^{J i t t e r} R(st?,at?)=wt?VtThrput??wd?VtRTT??wj?VtJitter?
V t T h r p u t = log ? ( ?Thrput?  ̄ t + 1 ) V_{t}^{T h r p u t}=\log \left(\overline{\text { Thrput }}_{t}+1\right) VtThrput?=log(?Thrput??t?+1)
V t R T T = log ? ( R T T  ̄ t + 1 ) V_{t}^{R T T}=\log \left(\overline{R T T}_{t}+1\right) VtRTT?=log(RTTt?+1)
V t Jitter? = log ? ( Δ R T T t + 1 ) V_{t}^{\text {Jitter }}=\log \left(\Delta R T T_{t}+1\right) VtJitter??=log(ΔRTTt?+1)
其中,一般设置 w t = 0.5 , w d = 1 , w t = 0.2 w_{t}=0.5,w_{d}=1,w_{t}=0.2 wt?=0.5,wd?=1,wt?=0.2??,也可视具体情况进行调整。
4. 实现
4.1 慢启动
仿照其他CC算法中的慢启动阶段,发送方用一个保守的值来初始化拥塞窗口的大小,然后将每个RTT的发送速率加倍,直到发生丢包。在第一个丢包事件发生后,NeuRoc退出慢启动,进入基于学习的CC学习阶段。
4.2 系统参数

采用全连接的神经网络,每个网络都有2个隐藏层,每层有128个神经元,并使用ReLU激活函数。学习率设为0.001。
4.3 Cold-Start
初始化
神经网络A和Q由随机参数初始化,将拥塞窗口调整的默认动作设定为 ?cwnd? = a t ? Thrput ? max ? ? R T T m i n \text { cwnd }=a_{t} * \operatorname{Thrput}_{\max } * R T T_{m i n} ?cwnd?=at??Thrputmax??RTTmin???, a t a_{t} at???从{ 0.75, 1, 1.25 }中随机抽取,类似BBR的窗口调整策略。
探索
在开始时,每当代理被触发时,以 ρ \rho ρ? 的概率采取默认行动(模仿BBR的行为),以 1 ? ρ 1-\rho 1?ρ?的概率采取未优化的政策网络所返回的行动, ρ \rho ρ?? 取0.95。同时将观测数据存放于buffer中。
训练
当重放缓冲区不断被观测数据填满时,agent在运行时由后台守护进程进行训练。
执行
训练收敛后,我们设概率ρ = 0,使agent采取策略网络产生的所有动作。模型参数在执行期间定期更新。
通过这样的训练策略,DRL agent可以以cold-start的方式部署,像BBR一样开始执行,然后逐渐转移到训练良好的policy网络。
5. 性能评估
5.1 测试环境


用于评估的三种trace:
- Long-lived trace:生成10000个持续20-60秒的长效TCP流。生成的TCP流由mahimahi在瓶颈链路上进行记录和重放,以测试不同算法的性能。
- Hybrid trace:包括动态网络场景中的长寿命和短寿命的TCP流。具体来说,生成5000个持续时间为20-60秒的长流和5000个持续时间为200-2000毫秒的短流,并将它们随机地组合在一起,形成Hybrid trace
- Real-world trace:根据FCC提供的宽带数据集生成真实世界的跟踪。FCC数据集包含100多万个WiFi环境下的吞吐量跟踪,其中每个都记录了2100秒内的吞吐量测量(0.5~6Mbps之间)。基于该数据集,作者通过串联随机选择的trace,生成了10000个不同持续时间的TCP流,时间从1-1000秒不等。
5.2 不同变点检测方法

5.3 不同超参数之间的比较
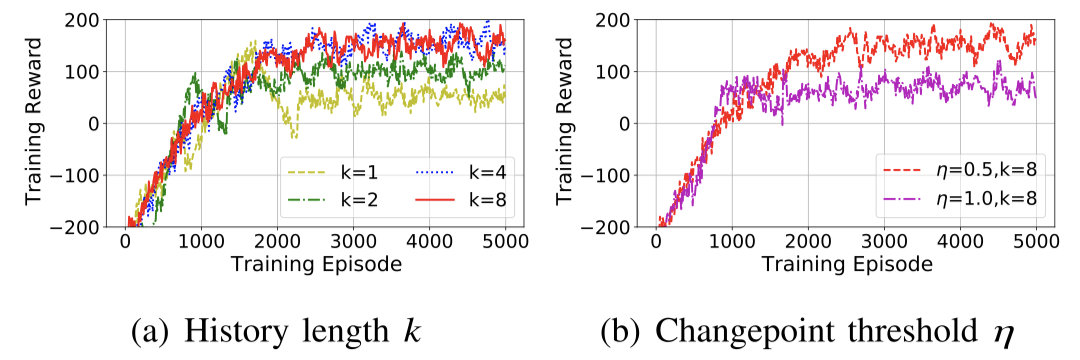
最终取 k = 8 , η = 0.5 k=8,\eta =0.5 k=8,η=0.5??
5.4 有无变点检测推断时间的比较

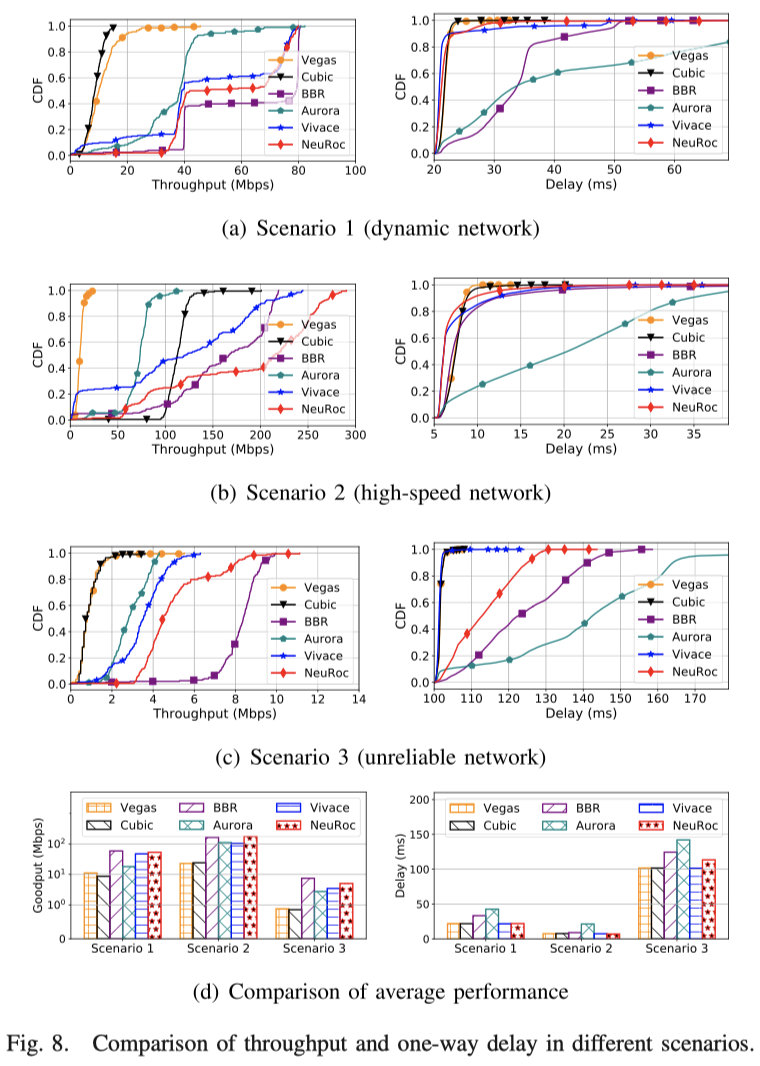
5.5 各种网络条件下算法之间的性能比较(略)
5.6 公平性比较
相同算法之间的公平性

公平性较高,可达0.96。
不同算法之间的公平性
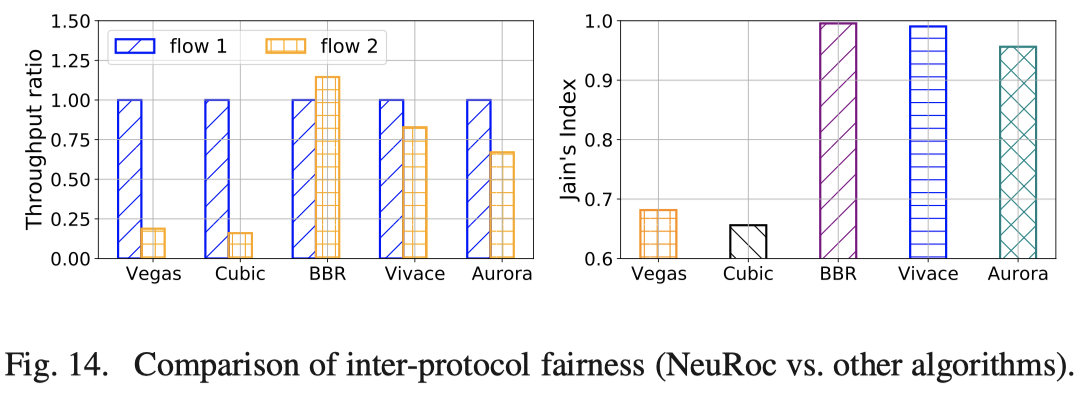
NeuRoc与BBR、Vivace和Aurora公平分享带宽,公平指数高于0.95。
5.7 最优工作点比较

NeuRoc实现了最佳的吞吐量-延迟权衡:它是最接近最优点的算法。
6. 不足与展望
- 众多超参数的选择比较困难
- 到目前为止,所有基于深度学习的TCP CC机制都是在用户层面实现的,因为在内核模式下缺乏对运行神经网络的支持。这种限制使得它无法被部署在商业服务器中并进行大规模测试。在具有硬件级加速的操作系统的内核模式下实现基于深度学习的TCP CC机制是真正关键的挑战。
- 训练需要大量数据,且在同一设备上训练的模型往往难以推广到其他设备上。