2021SC@SDUSC
概述
为了降低公开密钥系统中密钥和证书管理的复杂性,以色列科学家、RSA算法发明人之一Adi Shamir在1984年提出了标识密码(Identity-Based Cryptography)的理念。标识密码将用户的标识(如邮件地址、手机号码、QQ号码等)作为公钥,省略了交换数字证书和公钥过程,使得安全系统变得易于部署和管理,非常适合端对端离线安全通讯、云端数据加密、基于属性加密、基于策略加密的各种场合。2008年标识密码算法正式获得国家密码管理局颁发的商密算法型号:SM9(商密九号算法),为我国标识密码技术的应用奠定了坚实的基础。2016年国家密码局把SM9密码算法批准为国密算法,2017年进入ISO/IEC国际密码标准,标志着我国商用密码标准领域的竞争力进一步提升。
适用于互联网应用的各种新兴应用的安全保障。如基于云技术的密码服务、电子邮件安全、智能终端保护、物联网安全、云存储安全等等。这些安全应用可采用手机号码或邮件地址作为公钥,实现数据加密、身份认证、通话加密、通道加密等安全应用,并具有使用方便,易于部署的特点,从而开启了普及密码算法的大门。
作为IBC(标识密码算法)之一,SM9也包含数字签名、密钥交换、密钥封装和公钥加密四个功能。SM9与其他标识密码算法不同之处在于其不需要申请数字证书,把用户的公钥作为算法的标识,进而把验证证书的合法性这一环节改进成了简单的确认标识,标识作为公认的实体标志无可否认,故SM9算法优化了相关算法,变得较为简单。
IBC密码系统由五个部分构成:计算平台platform(例如椭圆曲线及其参数)、主密钥master key、密钥生成中心(即可信第三方)key generation center (KGC)、用户公钥(即标识)public key、用户私钥(由KGC生成)private key。
基本理论知识
有限域上的椭圆曲线
设q为大素数(>2^191 ),Fqm (m ≥1)是q"元有限域,定义在Fqm上的椭圆曲线方程为:y2=x3+ ax + b, a ,b ∈Fqm,且4a3+27b2≠0
椭圆曲线E(Fqm)是指:
E(Fqm)= {(x,y)|y2=x3 +ax + b,x,y ∈Fqm}∪{0}(即无穷远点)
#E(Fqm)表示椭圆曲线上点的数目,也称为椭圆曲线的阶。
加法群
在椭圆曲线上定义的加法可以构成一个加法群。
双线性对
椭圆曲线上的双线性对可以使用 Tate对、Weli对、Ate对、R-ate对
eid=01、02、03、04
设(G1,+)、(G2,+)和(Gt,·)是三个循环群,G1、G2和Gt的阶均为素数N,P1是G1的生成元,P2是G2的生成元,存在G2到G1的同态映射ψ使得ψ(P2)=P1;
双线性对e是G1×G2→Gt的映射,满足如下条件:
a)双线性性:对任意的P∈G1,Q∈G2,a , b∈ZN,有 e([a]P,[b]Q)=e(P,Q)ab
b)非退化性: e(P1,P2)≠1Gt;
c)可计算性:对任意的P∈G1,Q∈G2,存在有效的算法计算e(P,Q).
SM9算法的安全性依赖于双线性对的安全性,即椭圆曲线离散对数的安全性。双线性对的安全性主要建立在下面几个难解问题上:
问题一:双线性逆DH(BIDH)
问题二:判定双线性逆DH(DBIDH)
问题三:τ-双线性逆DH(τ-BDHI)
问题四:τ-Gap-双线性逆DH(τ-Gap-BDHI)
编码规则
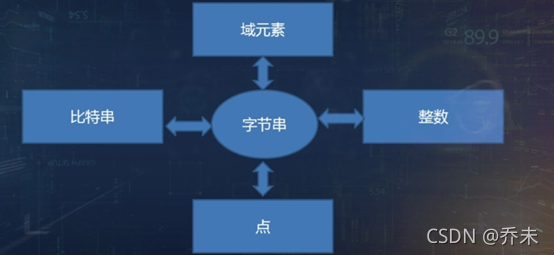
首先要明确上图五个名次的概念:
比特串:有序的0和1的序列。
字节串:有序的字节序列,8个比特为一个字节,最左边的比特为高位。
域元素:Fqm中的元素
椭圆曲线上的点:(x,y)或者无穷远点o
整数:字面意思,以一定的形式存在
整数与字节串

人话:把一个整数转化成256进制来表示,这样一位就在0~255之间,可以用8bits即一个字节表示,反之亦然。
比特串与字节串

人话:如果比特串位数正好为8的倍数,则以8为单位将比特串分开,转化为字节串;若不是8的倍数,左边补0,补成8的倍数之后再将其分开,转化为字节串。反之亦然。
域的元素与字节串

人话:如果m=1,即Fq是素域,其中的每一个元素都为整数,即为整数与字节串之间的转化;若m>1,则域中元素可以看成一个整数的分量,而每一个分量均为整数,只需要把每一个分量整数转化为字节串之后再拼接到一起即可。
椭圆曲线上的点与字节串


人话:两种转换方式:
1、 直接转换
曲线上的点的横纵坐标都为域内的整数,将横纵坐标的整数转化为字节串后拼接到一起即可
2、 压缩转换——一字节识别符+字节串
假设两个坐标的字节串分别为X,Y :
02||X,此时Y的最右边为0,压缩。
03||X,此时Y的最右边为1,压缩。
04 ||X||Y,非压缩。
06 ||X||Y,此时Y的最右边为0,混合。
07 ||X||Y,此时Y的最右边为1,混合。
学习总结
经过一段时间的资料搜集以及学习,认识了SM9加密系统与传统IBC的区别,了解并学习了算法内部椭圆曲线、双线性对和加法群等一些基础性的数学知识,对SM9算法有了初步的框架性认识,学习了在系统中整数、比特串、域元素和椭圆曲线上的点与字节串之间的相互转化方式,为下一步对相关代码以及SM9加密系统的进一步分析打下了一定的基础。