符号及辅助算法

下面对在SM9算法中用到的符号及函数进行了声明
在这里插入图片描述

在这里插入图片描述

源代码

在源程序\GmSSL-master\crypto\sm9\sm9_lcl.h中，找到了针对这些全局变量的定义：

私钥提取算法类型：

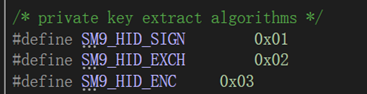
所用到的椭圆曲线类型：
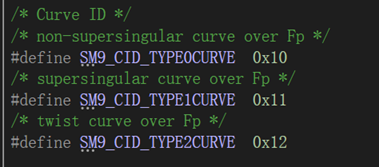
在这里插入图片描述
椭圆曲线上的双线性对类型（即eid）：

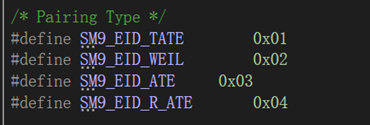
不同的嵌入度：

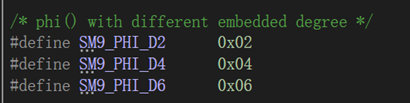
定义最大明密文长度：

源文件中还有其他函数及变量声明，在此不一一赘述。

用户A私钥的生成过程

用户A私钥的生成过程如下：
（1） KGC首先在有限域FN上计算t1=H1(IDA|| hid ,N)+ks ,若t =0则需重新产生签名主私钥,计算和公开签名主公钥,并更新已有用户的签名私钥（小概率事件，大多数情况下可以忽略）
（2） KGC计算t2=ks·t1-1mod N
（3）然后计算dsA=[t2]P1。

签名主公钥的生成

Ppub-s=[ks]P2

数字签名的生成

生成过程如下：
A1:计算群GT中的元素g =e(P1,Ppub-s. )
A2:产生随机数r∈[1,N一1]
A3:计算群Gr中的元素ω = gr,将ω 的数据类型转换为比特串﹔
A4 :计算整数h= H2(M || ω ,N );
A5:计算整数l=(r—h )mod N,若l=0则返回A2;
A6:计算群G中的元素S=[l]dsA ;
A7:将h的数据类型转换为字节串,将S的数据类型转换为字节串,消息M的签名为(h ,S)。

在这里插入图片描述
其中A3、A6两步运算用到了离散对数的安全性，其复杂性分析较为复杂，对理解算法内容影响不大，不再在此分析。

签名的认证

认证过程如下：
B1:将h’的数据类型转换为整数,检验h’∈[1,N-1]是否成立,若不成立则验证不通过;
B2:将S’的数据类型转换为椭圆曲线上的点﹐检验S’∈G是否成立,若不成立则验证不通过;
B3:计算群GT中的元素g =e(P1,Ppub- s )﹔
B4 :计算群GT中的元素t= gh’﹔
B5:计算整数h=H1 (IDA || hid ,N );
B6:计算群G2:中的元素P=[h1]P2+Ppub-s ;
B7:计算群GT中的元素u = e(S’ ,P);
B8:计算群GT中的元素ω’= u·t ,将w’的数据类型转换为比特串;
B9 :计算整数h2= H2(M’||ω‘,N) ,检验h2=h’是否成立,若成立则验证通过;否则验证不通过。

在这里插入图片描述
下面进行签名认证正确性的相关推导：
w’ = u·t
=e(S’ ,P)gh’
=e(S’,[h1]P2 + Ppub-s) gh’
=e([r - h’]dsA , [h1]P2 + Ppub-s) gh’
=e([r - h’][ks · (h1+ks)-1]P1 , [h1]P2 + Ppub-s) gh’
=e([r - h’][ks · (h1+ks)-1]P1 , [h1][ks-1]Ppub-s + Ppub-s) gh’
=e(P1,Ppub-s)^{(r-h’)(ks*(h1+ks)}^-1)(h1* ks-1+1) · gh’
=g^{(r-n")(h1+ks)}^-1 (h1+ks) gh’
=gr
=w