许多 SSL 方法中, 一致性正则化是个非常好的选择, 其优越的效果在 UDA, ICT, VAT 等算法中得到了验证, 不过这种方法十分依赖对数据的特定增强. 除此之外, 另一种基于熵最小化的方法, 即伪标签, 则不需要这种前提, 不过可能出现错误的高置信度预测, 而影响模型整体的效果. 因此, 提出不确定性感知的伪标签选择(UPS)框架, 该框架通过大幅减少训练过程中遇到的噪声量来提高伪标签的准确性, 并且在 UPS 中, 可以生成负伪标签(negative pseudo-labels).
SSL 的一个常见假设是决策边界应该位于低密度区域. 基于一致性正则化(Consistency Regularization)的方法通过使网络输出不受输入扰动(一般情况下, 扰动比较微弱)的影响来实现这一点. 然而, 这些方法的问题在于它们通常依赖于一组丰富的数据增强, 例如仿射变换, 剪切和图像中的颜色抖动等, 这限制了其在视频和医学图像领域的能力, 因为在这领域上的增强效果较差.
基于伪标签(Pseudo-Label)的方法选择具有高置信度的未标记样本作为训练目标, 这可以看作是熵最小化(Entropy Minimization)的一种形式, 它降低了决策边界处数据点的密度. 与一致性正则化相比, 伪标签的一个优点是它本身不需要增强, 并且通常可以应用于大多数领域. 由于神经网络的校准不佳, 许多选择的预测结果是不正确的, 糟糕的网络校准会产生错误的伪标签样本, 导致训练噪声增加. 通过实验发现, 选择具有低不确定性的预测可以大大降低校准不良的影响, 提高泛化能力.
1. 简介
受不确定性估计(Uncertainty estimation)和 Negative Learning(NL) 启发, 提出了一种不确定性感知伪标签选择(UPS)框架, 该框架利用预测不确定性来指导伪标签选择过程. UPS 不需要特定模式的增强, 并且可以在其选择过程中利用大多数不确定性估计方法, 如论文中使用的 MC-dropout. 此外, UPS 允许创建负伪标签 Negative Pseudo Label(即表示不属于该数据的标签). 如果网络以高置信度和高确定性预测某个不存在类, 则可以为该样本分配负标签.
题外话: 最近的比较厉害的 SSL 方法将一致性正则和伪标签集合起来, 例如 MixMatch, ReMixMatch, FixMatch, FeatMatch, FlexMatch, AggMatch.
2. 符号系统
- D L = { { ( x ( i ) , y ( i ) ) } } i = 1 N L D_L=\{\{(x^{(i)},y^{(i)})\}\}_{i=1}^{N_L} DL?={{(x(i),y(i))}}i=1NL?? 为有标签数据集, 其中 y ( i ) = [ y 1 ( i ) , … y C ( i ) ] ? { 0 , 1 } C y^{(i)}=[y_1^{(i)},\dots y_C^{(i)}] \subseteq\{0,1\}^C y(i)=[y1(i)?,…yC(i)?]?{0,1}C 表示 C C C 个类别. y C ( i ) = 0 y^{(i)}_C=0 yC(i)?=0 表示不存在类 C C C, y C ( i ) = 1 y^{(i)}_C=1 yC(i)?=1 表示存在类 C C C, 其实就是 one-hot 标签形式.
- D U = { x ( i ) } i = 1 N U D_U=\{x^{(i)}\}_{i=1}^{N_U} DU?={x(i)}i=1NU?? 为无标签数据集, 其中有 N U N_U NU? 个样本. 通过 D L D_L DL? 生成伪标签 y ~ i \tilde{y}^i y~?i.
- 基于伪标签的 SSL 方法在数据集 D ~ = { ( x ( i ) , y ~ ( i ) ) } i = 1 N L + N U \tilde{D}=\{(x^{(i)},\tilde{y}^{(i)})\}_{i=1}^{N_L+N_U} D~={(x(i),y~?(i))}i=1NL?+NU?? 上学习参数化模型 f θ f_\theta fθ?. 其中在有标记数据集上时 y ~ ( i ) = y ( i ) \tilde{y}^{(i)}=y^{(i)} y~?(i)=y(i).
3. 伪标签生成
令
p
(
i
)
p^{(i)}
p(i) 是在样本
x
(
i
)
x^{(i)}
x(i) 上训练网络的输出概率,
p
c
(
i
)
p^{(i)}_c
pc(i)? 表示样本中存在类别
c
c
c 的概率. 使用这些输出概率, 可以为
x
(
i
)
x^{(i)}
x(i) 生成伪标签:
y
~
c
(
i
)
=
1
[
p
c
(
i
)
≥
γ
]
(1)
\tilde{y}_c^{(i)}=\mathbb{1}[p_c^{(i)} \geq \gamma] \tag{1}
y~?c(i)?=1[pc(i)?≥γ](1)
其中
γ
∈
(
0
,
1
)
\gamma \in (0,1)
γ∈(0,1) 为固定的阈值. 当
γ
=
max
?
c
p
c
(
i
)
\gamma = \max_c p^{(i)}_c
γ=maxc?pc(i)? 时, 可以从式(1)导出传统的单标签伪标签. 对于多标签情况,
γ
=
0.5
\gamma = 0.5
γ=0.5 将导致二元伪标签, 其中多个类可以存在一个样本中.
4. 伪标签选择
令
g
(
i
)
=
[
g
1
i
,
…
,
g
C
(
i
)
]
?
{
0
,
1
}
C
g^{(i)}=[g_1^{i},\dots,g_C^{(i)}] \subseteq \{0,1\}^C
g(i)=[g1i?,…,gC(i)?]?{0,1}C 表示第
i
i
i 个样本选择的伪标签, 若
g
c
(
i
)
=
0
g_c^{(i)}=0
gc(i)?=0 则表示
y
~
c
(
i
)
\tilde{y}^{(i)}_c
y~?c(i)? 没有被选择, 反之则被选择.
g
c
(
i
)
=
1
[
p
c
(
i
)
≥
τ
p
]
+
1
[
p
c
(
i
)
≤
τ
n
]
(2)
g_c^{(i)}=\mathbb{1}[p_c^{(i)} \geq \tau_p]+\mathbb{1}[p_c^{(i)} \leq \tau_n] \tag{2}
gc(i)?=1[pc(i)?≥τp?]+1[pc(i)?≤τn?](2)
其中
τ
p
\tau_p
τp?,
τ
n
\tau_n
τn? 分别表示正负标签的置信度阈值(在这里,
τ
p
≥
τ
n
\tau_p \geq \tau_n
τp?≥τn?). 如果
p
c
(
i
)
≥
τ
p
p_c^{(i)} \geq \tau_p
pc(i)?≥τp? 的概率分数足够高, 则选择正标签, 相反, 如果网络对一个其他类有足够信心:
p
c
(
i
)
≤
τ
n
p_c^{(i)} \leq \tau_n
pc(i)?≤τn?, 则选择为负标签.
参数化模型
f
θ
f_\theta
fθ? 在选定的伪标签子集上进行训练. 对于单标签分类, 在具有选定的正标签的样本上计算交叉熵损失(CE). 如果没有选择正标签, 则使用负标签, 使用负交叉熵损失(NCE):
L
N
C
E
(
y
~
(
i
)
,
y
^
(
i
)
,
g
(
i
)
)
=
?
1
s
(
i
)
∑
c
=
1
C
g
c
(
i
)
(
1
?
y
~
c
(
i
)
)
log
?
(
1
?
y
^
c
(
i
)
)
(3)
L_{NCE}(\tilde{y}^{(i)},\hat{y}^{(i)},g^{(i)})=-\frac{1}{s^{(i)}}\sum_{c=1}^Cg_c^{(i)}(1-\tilde{y}_c^{(i)})\log(1-\hat{y}_c^{(i)}) \tag{3}
LNCE?(y~?(i),y^?(i),g(i))=?s(i)1?c=1∑C?gc(i)?(1?y~?c(i)?)log(1?y^?c(i)?)(3)
其中,
s
(
i
)
=
∑
c
g
c
(
i
)
s^{(i)}=\sum_cg_c^{(i)}
s(i)=∑c?gc(i)? 为第
i
i
i 个样本选择的伪标签数量.
y
^
(
i
)
=
f
θ
(
x
(
i
)
)
\hat{y}^{(i)}=f_\theta(x^{(i)})
y^?(i)=fθ?(x(i)) 为模型输出. 融合正负标签, 使用修正的交叉熵损失:
L
B
C
E
(
y
~
(
i
)
,
y
^
(
i
)
,
g
(
i
)
)
=
?
1
s
(
i
)
∑
c
=
1
C
g
c
(
i
)
[
y
~
c
(
i
)
log
?
(
y
^
c
(
i
)
)
+
(
1
?
y
~
c
(
i
)
)
log
?
(
1
?
y
^
c
(
i
)
)
]
(4)
L_{BCE}(\tilde{y}^{(i)},\hat{y}^{(i)},g^{(i)})=-\frac{1}{s^{(i)}}\sum_{c=1}^Cg_c^{(i)}[\tilde{y}_c^{(i)}\log(\hat{y}_c^{(i)})+(1-\tilde{y}_c^{(i)})\log(1-\hat{y}_c^{(i)})] \tag{4}
LBCE?(y~?(i),y^?(i),g(i))=?s(i)1?c=1∑C?gc(i)?[y~?c(i)?log(y^?c(i)?)+(1?y~?c(i)?)log(1?y^?c(i)?)](4)
L
B
C
E
L_{BCE}
LBCE? 同样可用在多标签分类中.
5. 不确定性感知伪标签选择
通过分析网络校正与模型对个体样本输出不确定性的关系, 得到结论: 当选择具有更多确定预测的伪标签时, 伪标签子集的校准误差大大降低. 其中, 衡量网络校正的指标为 Expected Calibration Error(ECE). 根据这一观察, 我们得出结论, 可以利用预测不确定性来抵消校准不良的影响. 因此, 通过利用网络预测的置信度和不确定性, 在训练中使用更准确的伪标签子集. 式(2)现在变为:
g
c
(
i
)
=
1
[
u
(
p
c
(
i
)
)
≤
κ
p
]
1
[
p
c
(
i
)
≥
τ
p
]
+
1
[
u
(
p
c
(
i
)
)
≤
κ
n
]
1
[
p
c
(
i
)
≤
τ
n
]
(5)
g_c^{(i)}=\mathbb{1}[u(p_c^{(i)})\leq \kappa_p]\mathbb{1}[p_c^{(i)} \geq \tau_p]+\mathbb{1}[u(p_c^{(i)})\leq \kappa_n]\mathbb{1}[p_c^{(i)} \leq \tau_n] \tag{5}
gc(i)?=1[u(pc(i)?)≤κp?]1[pc(i)?≥τp?]+1[u(pc(i)?)≤κn?]1[pc(i)?≤τn?](5)
其中
u
(
p
)
u(p)
u(p) 预测
p
p
p 的不确定性,
κ
p
\kappa_p
κp?,
κ
n
\kappa_n
κn? 分别为不确定阈值.
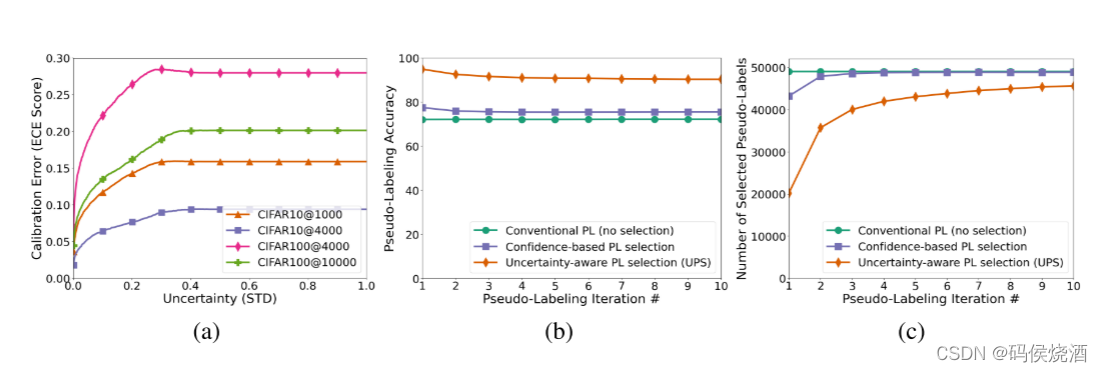
- a) 预测不确定性与预期校准误差 (ECE) 之间的关系. 在所有数据集中, 随着所选伪标签的不确定性降低, 所选子集的 ECE 也会降低.
- b) 传统伪标签 (PL)、基于置信度的选择 (Confidence PL) 和 UPS 之间的伪标签选择精度比较.
- c) 传统伪标签 (PL)、基于置信度的选择 (Confidence PL) 和 UPS 之间选择的伪标签数量的比较. 尽管 UPS 最初选择了一组较小的伪标签, 但通过最终的伪标签迭代, 它在训练中合并了大部分伪标签, 同时保持了更高的伪标签精度.
6. UPS 算法

- 1.在 D L D_L DL? 上训练神经网络 f θ , 0 f_{\theta,0} fθ,0?.
- 2.训练完成后, 网络对 D U D_U DU? 中的所有未标记数据生成预测结果.
- 3.根据式(1)从这些预测中创建伪标签, 使用 UPS(式 5)选择伪标签的子集.
- 4.使用选定的伪标签以及标记集 D ~ \tilde{D} D~ 来训练另一个网络 f θ , 1 f_{\theta,1} fθ,1?.
- 5.重复步骤2到步骤4, 直到收敛为止.