前言
前段时间跟队里某些同学一样学习了微积分,然后想练练手,练完手就出现了这篇文章…
概念
球的体积
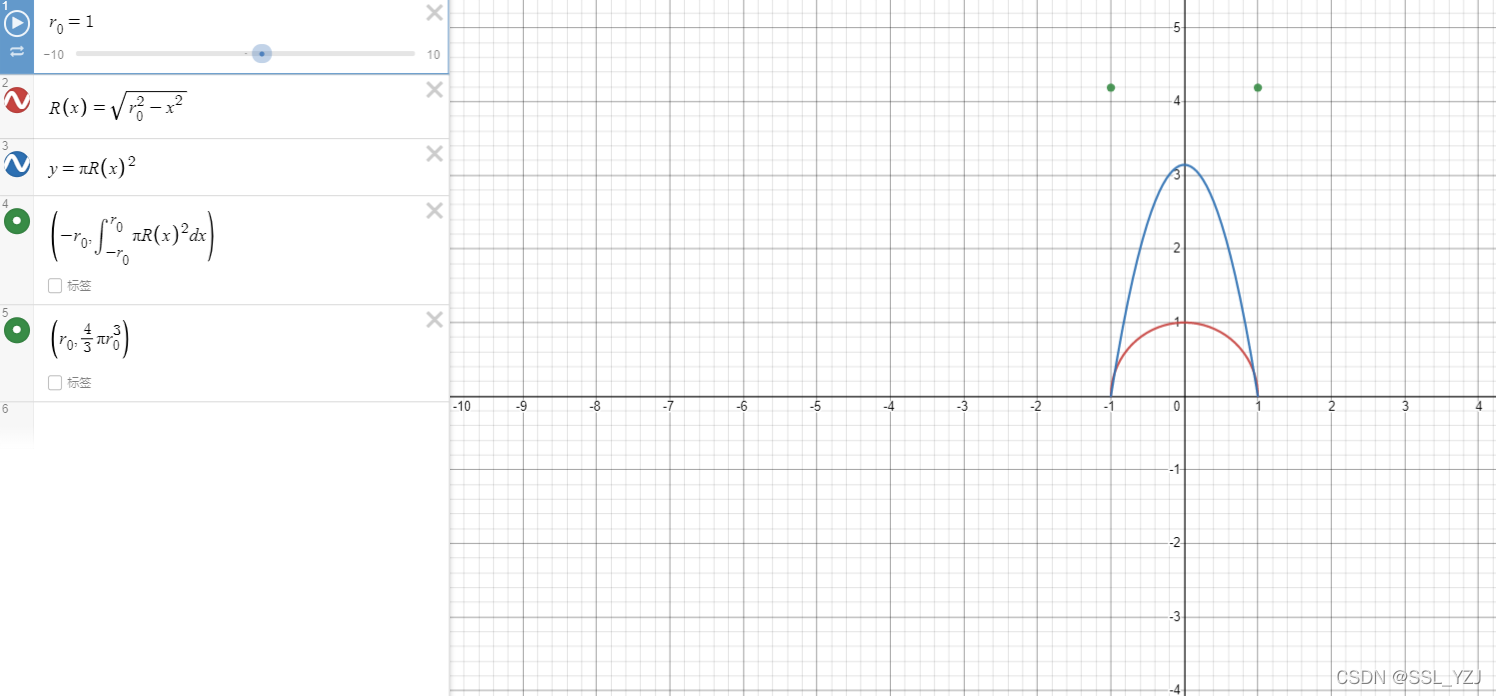
球的半径为 r r r,半径函数为 R ( x ) = r 2 ? x 2 R(x)=\sqrt{r^{2}-x^{2}} R(x)=r2?x2?,则体积为
V = ∫ ? r r π [ R ( x ) ] 2 d x V=\int^{r}_{-r}\pi[R(x)]^{2}dx V=∫?rr?π[R(x)]2dx
???? = ∫ ? r r π [ r 2 ? x 2 ] 2 d x \ \ \ \ =\int^{r}_{-r}\pi[\sqrt{r^{2}-x^{2}}]^{2}dx ????=∫?rr?π[r2?x2?]2dx
???? = ∫ ? r r π [ r 2 ? x 2 ] d x \ \ \ \ =\int^{r}_{-r}\pi[r^{2}-x^{2}]dx ????=∫?rr?π[r2?x2]dx
???? = π ∫ ? r r [ r 2 ? x 2 ] d x \ \ \ \ =\pi\int^{r}_{-r}[r^{2}-x^{2}]dx ????=π∫?rr?[r2?x2]dx
???? = π [ r 2 x ? x 3 3 ] ? r r \ \ \ \ =\pi[r^{2}x-\frac{x^{3}}{3}]^{r}_{-r} ????=π[r2x?3x3?]?rr?
???? = π [ ( r 3 ? r 3 3 ) ? ( ? r 3 + r 3 3 ) ] \ \ \ \ =\pi[(r^{3}-\frac{r^{3}}{3})-(-r^{3}+\frac{r^3}{3})] ????=π[(r3?3r3?)?(?r3+3r3?)]
???? = π [ r 3 ? r 3 3 + r 3 ? r 3 3 ] \ \ \ \ =\pi[r^{3}-\frac{r^3}{3}+r^{3}-\frac{r^{3}}{3}] ????=π[r3?3r3?+r3?3r3?]
???? = 4 3 π r 3 \ \ \ \ =\frac{4}{3}\pi r^{3} ????=34?πr3
圆锥的体积
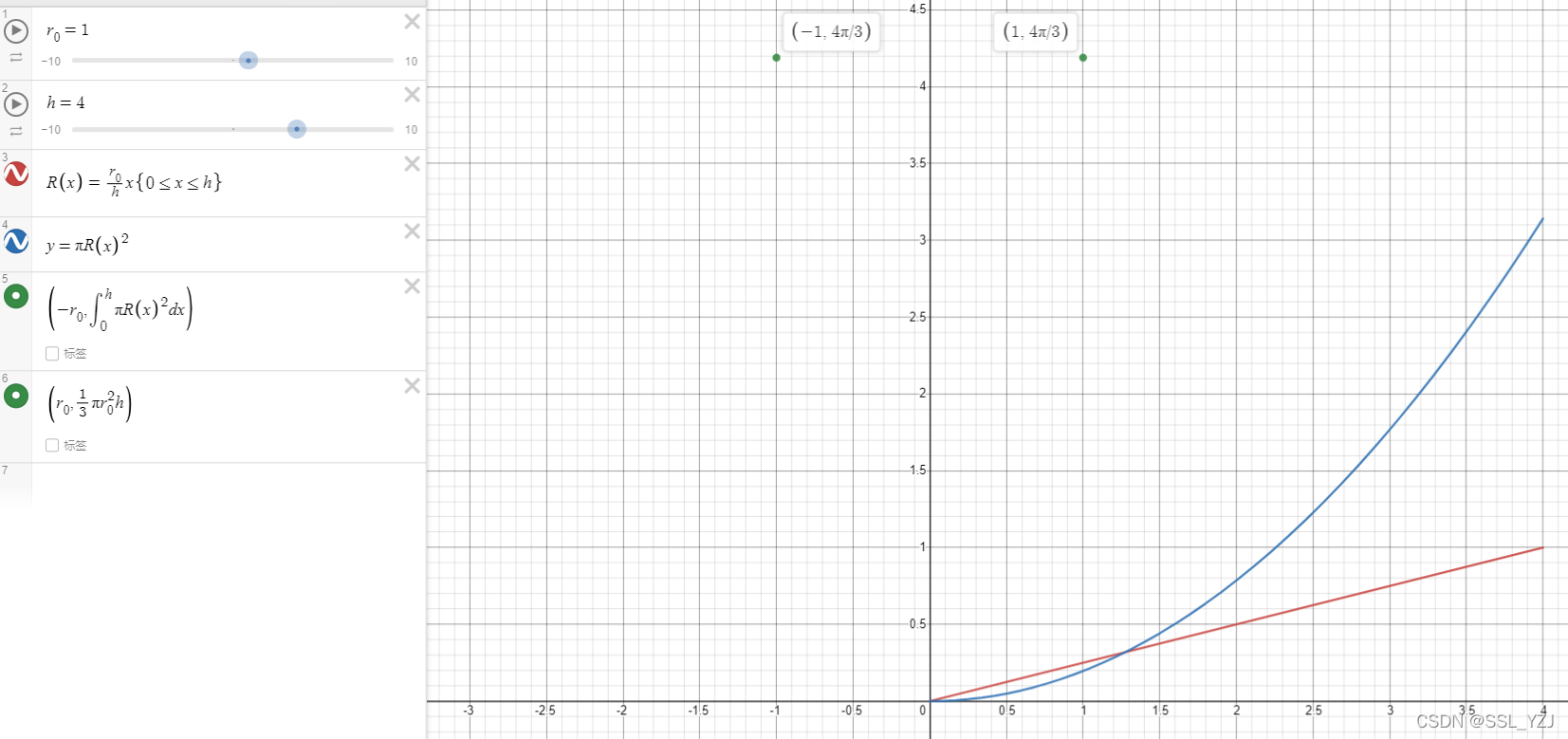
圆锥的高为 h h h,底面半径为 r r r,半径函数为 R ( x ) = t a n ( α ) × x = r h × x R(x)=tan(\alpha)\times x=\frac{r}{h}\times x R(x)=tan(α)×x=hr?×x,则体积为
V = ∫ 0 h π [ R ( x ) ] 2 d x V=\int^{h}_{0}\pi[R(x)]^{2}dx V=∫0h?π[R(x)]2dx
???? = ∫ 0 h [ π × r 2 h 2 × x 2 ] d x \ \ \ \ =\int^{h}_{0}[\pi\times\frac{r^{2}}{h^{2}}\times x^{2}]dx ????=∫0h?[π×h2r2?×x2]dx
???? = π r 2 h 2 × ∫ 0 h [ x 2 ] d x \ \ \ \ =\pi\frac{r^{2}}{h^{2}}\times\int^{h}_{0}[x^{2}]dx ????=πh2r2?×∫0h?[x2]dx
???? = π r 2 h 2 × [ x 3 3 ] 0 h \ \ \ \ =\pi\frac{r^{2}}{h^{2}}\times[\frac{x^{3}}{3}]^{h}_{0} ????=πh2r2?×[3x3?]0h?
???? = π r 2 h 2 × h 3 3 \ \ \ \ =\pi\frac{r^{2}}{h^{2}}\times\frac{h^{3}}{3} ????=πh2r2?×3h3?
???? = 1 3 π r 2 h \ \ \ \ =\frac{1}{3}\pi r^{2}h ????=31?πr2h
正三棱锥的体积
先求面积函数(等边三角形的边长和面积的关系),看下图:
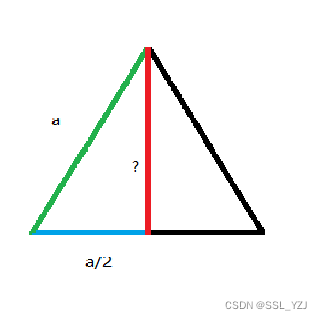
设一个等边三角形的边长为
a
a
a,则其面积为
S
=
1
2
a
h
=
1
2
a
×
a
2
?
(
a
2
)
2
=
1
2
a
×
a
2
?
a
2
4
=
1
2
a
×
3
a
2
4
=
1
2
a
×
3
a
2
=
3
a
2
4
S=\frac{1}{2}ah=\frac{1}{2}a\times\sqrt{a^{2}-(\frac{a}{2})^{2}}=\frac{1}{2}a\times\sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{1}{2}a\times\sqrt{\frac{3a^{2}}{4}}=\frac{1}{2}a\times\frac{\sqrt{3}a}{2}=\frac{\sqrt{3}a^{2}}{4}
S=21?ah=21?a×a2?(2a?)2?=21?a×a2?4a2??=21?a×43a2??=21?a×23?a?=43?a2?
所以,面积函数
S
(
x
)
=
3
(
a
h
x
)
2
4
S(x)=\frac{\sqrt{3}(\frac{a}{h}x)^{2}}{4}
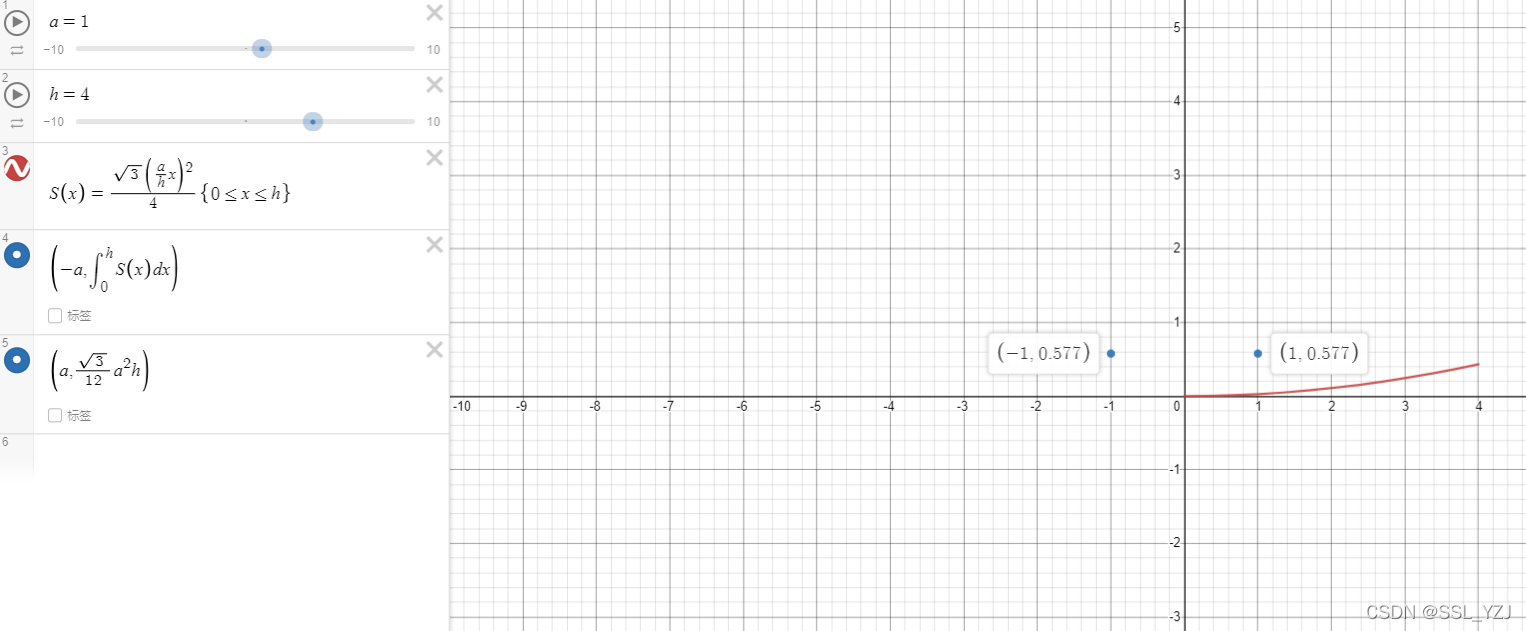
S(x)=43?(ha?x)2?,三棱锥的高为
h
h
h,底面边长为
r
r
r,则体积为
V = ∫ 0 h S ( x ) d x V=\int^{h}_{0}S(x)dx V=∫0h?S(x)dx
???? = ∫ 0 h [ 3 ( a h x ) 2 4 ] d x \ \ \ \ =\int^{h}_{0}[\frac{\sqrt{3}(\frac{a}{h}x)^{2}}{4}]dx ????=∫0h?[43?(ha?x)2?]dx
???? = ∫ 0 h 3 a 2 4 h 2 × x 2 \ \ \ \ =\int^{h}_{0}\frac{\sqrt{3}a^{2}}{4h^{2}}\times x^{2} ????=∫0h?4h23?a2?×x2
???? = 3 a 2 4 h 2 ∫ 0 h x 2 d x \ \ \ \ =\frac{\sqrt{3}a^{2}}{4h^{2}}\int^{h}_{0}x^{2}dx ????=4h23?a2?∫0h?x2dx
???? = 3 a 2 4 h 2 [ x 3 3 ] 0 h \ \ \ \ =\frac{\sqrt{3}a^{2}}{4h^{2}}[\frac{x^{3}}{3}]^{h}_{0} ????=4h23?a2?[3x3?]0h?
???? = 3 a 2 4 h 2 × h 3 3 \ \ \ \ =\frac{\sqrt{3}a^{2}}{4h^{2}}\times \frac{h^{3}}{3} ????=4h23?a2?×3h3?
???? = 3 12 a 2 h \ \ \ \ =\frac{\sqrt{3}}{12}a^{2}h ????=123??a2h
观察得,圆锥的体积等于等底等高的圆柱的体积的
1
3
\frac{1}{3}
31?,三棱锥的体积也等于等底等高的三棱柱的体积的
1
3
\frac{1}{3}
31?,所以是否任意形状的锥体的体积都是与其等底等高的柱体的体积的
1
3
\frac{1}{3}
31?呢?我们再推得四棱锥的体积公式观察结果。
正四棱锥的体积
正四棱锥的底面边长为 a a a,高为 h h h,面积公式 S ( x ) = ( a h x ) 2 S(x)=(\frac{a}{h}x)^2 S(x)=(ha?x)2则体积为
V = ∫ 0 h S ( x ) d x V=\int^{h}_{0}S(x)dx V=∫0h?S(x)dx
???? = ∫ 0 h ( a h x ) 2 d x \ \ \ \ =\int^{h}_{0}(\frac{a}{h}x)^{2}dx ????=∫0h?(ha?x)2dx
???? = ∫ 0 h ( a 2 h 2 x 2 ) d x \ \ \ \ =\int^{h}_{0}(\frac{a^{2}}{h^{2}}x^{2})dx ????=∫0h?(h2a2?x2)dx
???? = a 2 h 2 ∫ 0 h x 2 d x \ \ \ \ =\frac{a^{2}}{h^{2}}\int^{h}_{0}x^{2}dx ????=h2a2?∫0h?x2dx
???? = a 2 h 2 [ x 3 3 ] 0 h \ \ \ \ =\frac{a^{2}}{h^{2}}[\frac{x^{3}}{3}]^{h}_{0} ????=h2a2?[3x3?]0h?
???? = a 2 h 2 × h 3 3 \ \ \ \ =\frac{a^{2}}{h^{2}}\times\frac{h^{3}}{3} ????=h2a2?×3h3?
???? = 1 3 a 2 h \ \ \ \ =\frac{1}{3}a^{2}h ????=31?a2h
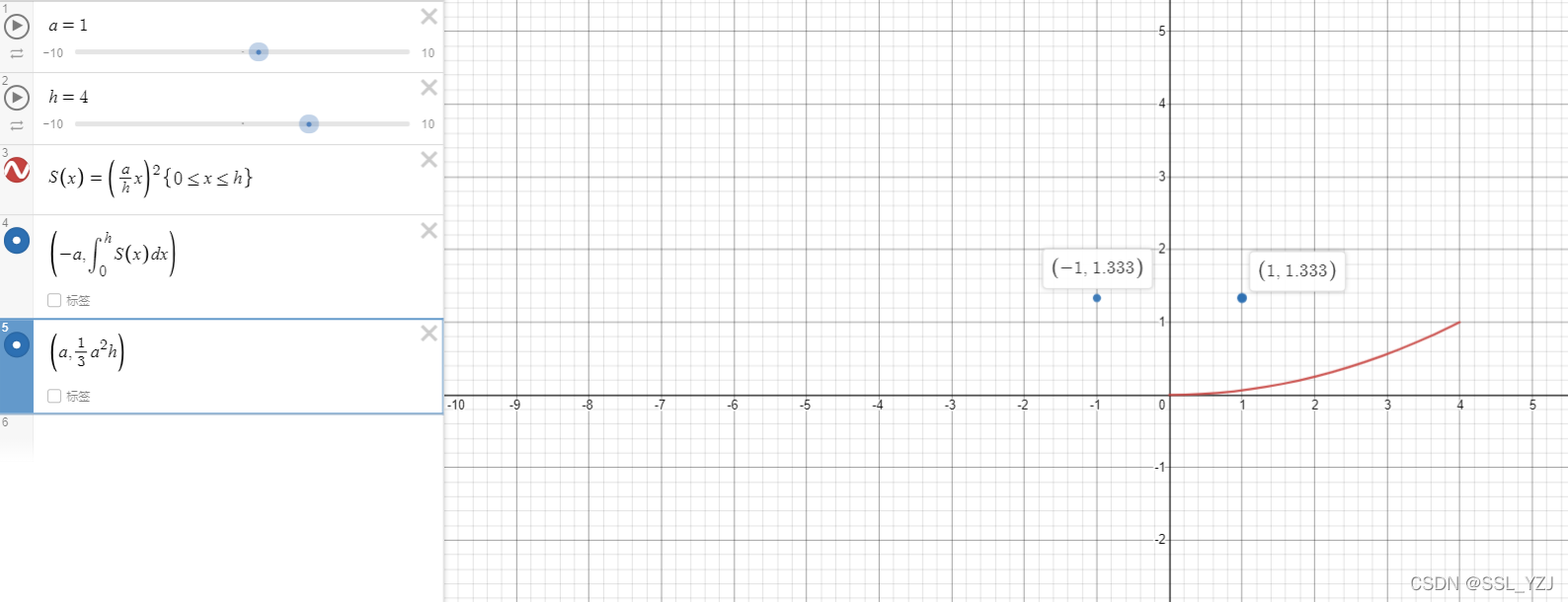
很明显,正四棱锥的体积也等于等底等高的正四棱柱(长方体)的体积的
1
3
\frac{1}{3}
31?,那么,我们能否得到任意形状的锥体的体积都是与其等底等高的柱体的体积的
1
3
\frac{1}{3}
31?呢?
未完待续…
未完待续…