[XJTU计算机网络安全与管理]第二讲 密码技术
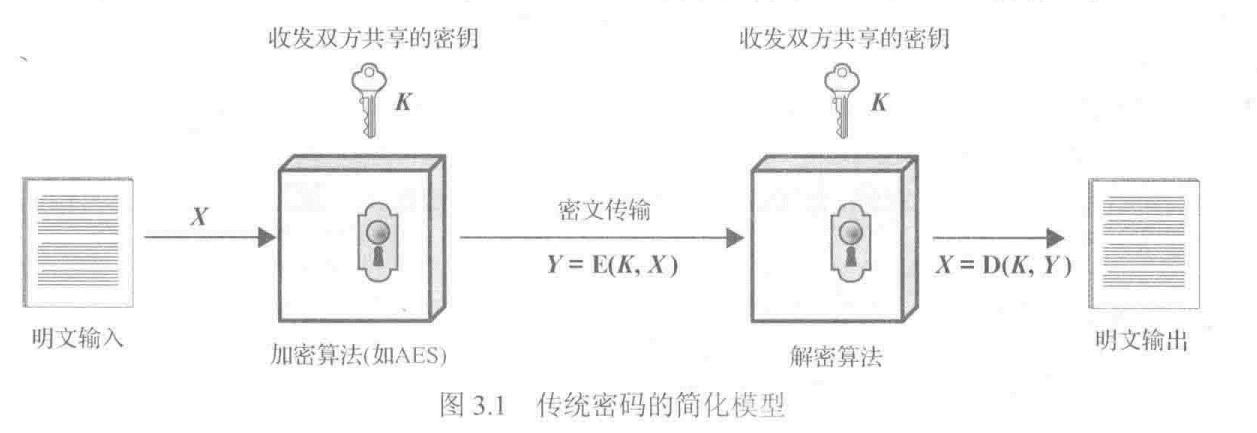
密码学(密码术)作为许多安全机制(如加密,解密,验证等)的一项基本元素,在信息安全中具有非常重要的地位。其地位如图所示——会画图

一、加密技术概述
Cryptography源自希腊语单词“kryptos”(hidden)与“graphia”(writing)。
定义:密码学是针对如机密性,数据完整性,实体认证,数据源认证等信息安全课题进行的数学技术研究。
密码学研究的主要目标是:
- 机密性
- 数据完整性
- 认证(真实性)
- 不可抵赖(可审计性)
密码学的主要研究方向可分为如下四类(了解即可):
- 对称加密技术
- 非对称加密技术
- 哈希函数
- 伪随机数生成
二、对称加密Symmetric Encryption
- 或私钥加密/常规加密/单密钥加密
- 发送方和接收方使用相同的密钥
- 所有传统的加密算法都是对称加密
- 20世纪70年代(公钥加密提出)之前是唯一的类型
- 目前仍旧具有广泛的应用
基本术语
明文(plaintext) - 源消息
密文(ciphertext) - 编码后的消息
cipher (密码,加密技术)- 将明文转换为密文的算法
密钥(key) - 加密程序所使用,仅被发送者/接收者所知的信息。
加密 encipher (encrypt) – 将原文转换为密文
解密 decipher (decrypt) – 将密文恢复为原文
密码编码学 cryptography – 针对加密原理/方法的研究
密码分析 cryptanalysis (codebreaking) – 在不知道密钥的情况下对密文进行解密的原则/方法的研究
密码研究 cryptology – 密码编码学与密码分析的领域之和
P:明文
C:密文
E K e ( P ) → C : ? 加 密 E_{K_e}(P)\rightarrow C:\ 加密 EKe??(P)→C:?加密
D K d ( C ) → P : ? 解 密 D_{K_d}(C)\rightarrow P:\ 解密 DKd??(C)→P:?解密
要求
对称加密的安全使用有下面两个要求
一个健壮的加密算法
密码仅为发送方*/*接收方所知
数学表示:
C
=
E
(
K
e
,
P
)
P
=
D
(
K
d
,
C
)
P
=
D
(
K
d
,
E
(
K
e
,
P
)
)
=
P
C=E(K_e,P)\qquad P=D(K_d,C)\\ P=D(K_d,E(K_e,P))=P
C=E(Ke?,P)P=D(Kd?,C)P=D(Kd?,E(Ke?,P))=P
算法是公开的
提供一个安全信道以分享密钥
密码编码学
我们刻画/描述一个密码系统通常可以通过:
1?? 加密操作的方法
替代/转置/乘积
2?? 使用的密钥数
单密钥或私钥/双密钥或公钥
3?? 明文的处理方式
块加密/流加密
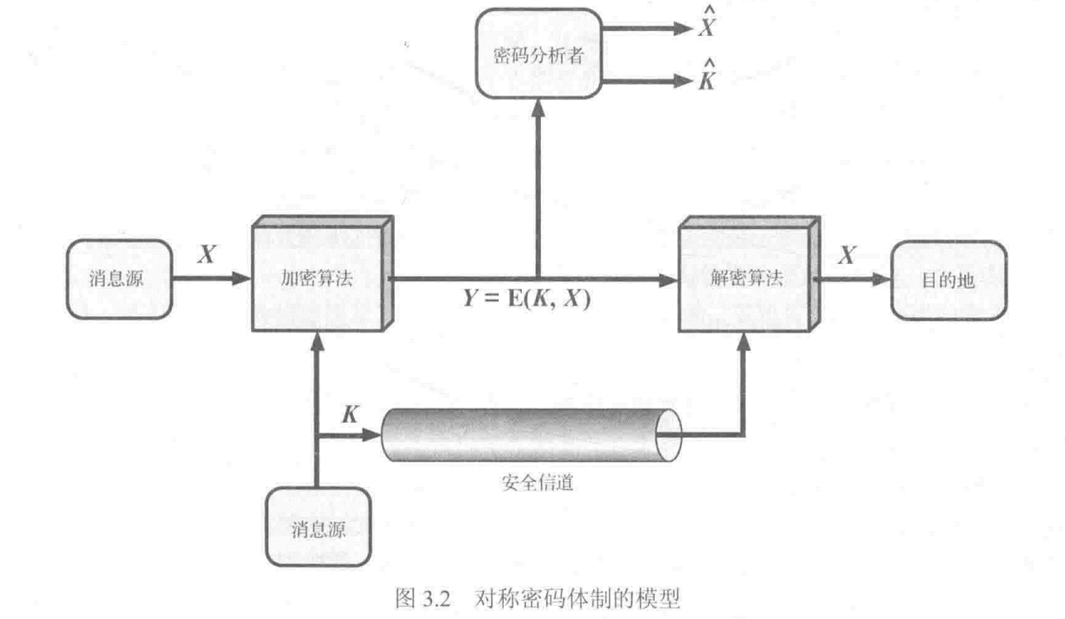
密码分析学与密码攻击
密码分析可看作是试图发现密钥或原文的过程
密码分析的原则:
破译改密码的成本超过被加密信息的价值
破译该密码的时间超过该信息有用的生命周期
密码分析的方法:
用密码分析方法的破解(cryptanalytic attack)
暴力破解 ( brute-force attack)
密码攻击的类型(了解即可)
| 攻击的类型 | 密码破译者已知的 |
|---|---|
| 仅有密文 | 加密算法 带破译的密文 |
| 已知明文 | 加密算法 待破译的密文 由密钥形成的一个或多个明文-密文对 |
| 选择明文 | 加密算法 待破译的密文 有密码破译者选择的明文消息,连同它对应的由其密钥生成的密文 |
| 选择密文 | 加密算法 待破译的密文 由密码破译者选择的猜测性的密文,连同它对应的由密钥生成的已破译的明文 |
| 选择文本 | 加密算法 待破译的密文 由密码破译者选择的明文消息,连同它对应的由密码生成的密文 由密码破译者选择猜测性的密文,连同它对应的由密钥生成的已破译的明文 |
无条件安全:不论计算机的能力与时间如何,由于密文所提供的信息不足以唯一的确定相应的明文,密码均不能被破解。
计算安全:所具备的受限的计算资源不足以破解密码
三、古典替代密码
明文中的每一个元素(比特,字母,比特组合或字母组合)被映射为另一个元素。
这里可能是字母被替换为其他字母或符号
也可能是位组合被替换为另外的位组合
凯撒码Caesar
已知的最早的替代码
Julius Caesar
最初应用于军事,将每个字母替换为其后的第三个字母。
例:
meet me after the toga party
PHHW PH DIWHU WKH WRJD SDUWB
其变化可描述为以下方法
a b c d e f g h i j k l m n o p q r s t u v w x y z
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
我们可以数学的给字母以如下表示
a b c d e f g h i j k l m n o p q r s t u v w x y z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
凯撒码可以表示为
c = E§ = (p + k) mod (26)
p = D? = (c – k) mod (26)
特点分析
只有26个可能的密码,可以很容易的依次验证——暴力破解
对于已知密文,只需依次移动字母
当明文产生时需要能够识别
单表代替密码
比单纯的移动字母表要更进一步
可以任意的进行字幕替换
每个原文字符都可以被映射为一个任意的密文字符
密码长度为26个字母
例:
Plain: abcdefghijklmnopqrstuvwxyz
Cipher: DKVQFIBJWPESCXHTMYAUOLRGZN
Plaintext: ifwewishtoreplaceletters
Ciphertext: WIRFRWAJUHYFTSDVFSFUUFYA
安全性说明
总共的密码数为26!总数大于 4 x × 1 0 26 4x\times10^{26} 4x×1026
有如此多的密码,是不是更安全呢?
事实上是错误的。
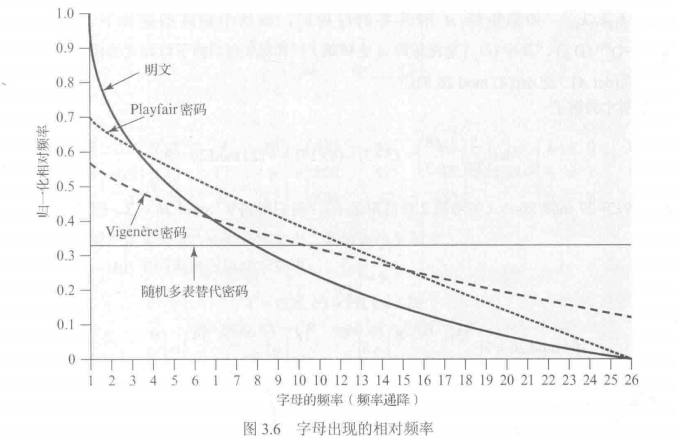
主要问题在于语言的特性——某些字母出现的频率高,有些用的少

关键概念-单一字母替代码不会改变字母的出现的频率
该特点由阿拉伯科学家于公元9世纪发现
计算字母出现频率
将计算值于已知值进行对比
如果我们查看凯撒码的峰/槽值我们有
峰值在A-E-I,NO,RST
槽值在JK,X-Z
应当针对每个字母结合二元组,三元组进行验证
Playfair 密码
单一替代码虽然增加了密码数量但并没有增加安全性
一种改进的方案是多字母加密
Playfair即是一例
由英国科学家Charles Wheatstone 1854年发明用的是他的朋友的名字Barron Playfair
Playfair矩阵
| M | O | N | A | R |
|---|---|---|---|---|
| C | H | Y | B | D |
| E | F | G | I/J | K |
| L | P | Q | S | T |
| U | V | W | X | Z |
本例使用的密钥词是monarchy。填充矩阵的方法是:首先将密钥词(去掉重复字母)从左至右从上至下填在矩阵格子中,再将剩余的字母按字母表的顺序从左至右、从上至下填在矩阵剩下的格子里。字母I和J暂且当成一个字母。对明文按如下规则一次加密两个字母:
1?? 如果该字母对的两个字母是相同的,那么在它们之间加一个填充字母,比如x。例如balloon先把它变成ba Ix lo on这样四个字母对
2?? 落在矩阵同一行的明文字母对中的字母由其右边的字母来代替,每行中最右边的一个字母就用该列中最左边的第一个字母来代替,比如ar变成RM
3?? 落在矩阵同一列的明文字母对中的字母由其下面的字母来代替,每行中最下面的一个字母就用该列中最上面的第一个字母来代替,比如mu变成CM。
4?? 其他的每组明文字母对中的字母按如下方式代替,该字母所在行为密文所在行,另一字母所在列为密文所在列。比如hs变成BP,ea变成IM(或JM)。(对角变对角)
特点
比单一字母替换安全性好
频率表项增加到了26x26=676
曾被广泛应用多年(如第一次世界大战)
提供几百个字母下可破解
仍能够保留部分明文结构特征
多字母密码
性质:使用一系列相关的单字母替代规律
一个密钥决定对一个给定的变换选择那种特定的规则
Vigenère码:
相隔的单字母替代规则集合由26个凯撒码组成
加密过程为:给定一个密钥x一个明文y,密文为x与y的交叉点V
key: deceptivedeceptivedeceptive
plaintext: wearediscoveredsaveyourself
ciphertext:ICVTWQNGRZGVTWAVZHCQYGLMGJ
安全性
每个明文字母都对应多个密文
字母的统计信息被隐藏了
但并非完全隐藏
开始首先统计字母出现频率。查看是否为单一替代码。如果不是则通过确定关键词长度来继续分析:
比如前面的例子通过red的密文VTM猜测关键词长度为9,然后可以通过一直频率特征考虑攻击
一次一密One-Time Pad
采用与明文一样长的随机串为关键词
具备很强的安全性,统计学特征被隐藏
一次一密
密钥的生成与共享是存在的难题
没多大用——难以把密钥传过去
四、置换技术
该方法通过将字符重新排列隐藏信息
并不改变使用的字符
该方案可以通过原文,密文中字符出现的频率相同进行识别
栅栏技术
按照对角线顺序写出明文,然后按照行的顺序读取作为密文,例如:用深度为2的栅栏技术加密信息“meet me after the toga party”,可写作
m e m a t r h t g p r y
e t e f e t e o a a t
密文为:MEMATRHTGPRYETEFETEOAAT
行置换技术
一个更复杂的方案是:
将消息按照特定的列数写成矩阵形式
按照密钥值依次读出按照行排列
Key: 3 4 2 1 5 6 7
Plaintext: a t t a c k p
? o s t p o n e
? d u n t i l t
? w o a m x y z
Ciphertext: TTNAAPTMTSUOAODWCOIXKNLYPETZ
乘积
通过将加密方案复合可以增大破解的难度。
单纯的替代组合可以得到更复杂的替代
单纯的置换组合可以得到更复杂的置换
置换之后进行替代将构成新的难以破解的密码方案。(这也是传统密码学向现代密码学过度的桥梁)
五、转子机
在现代密码学之前,转子机是最常用的复杂加密设备
第二次世界大战中被广泛使用:德国的 Enigma, 日本的Purple
提供了非常复杂的替代密码
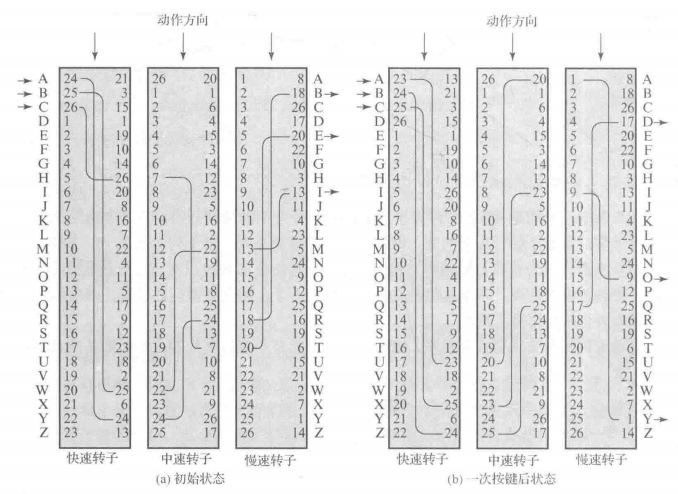
由一系列独立转动的圆柱体构成。每个提供一个替代加密,并且在每次击键后能够进行更改。
参考资料
[1] 西安交通大学计算机网络安全与管理2022年春PPT 田暄
[2] 密码编码学与网络安全(第七版),William Stallings著,王后珍等译