原理
根据欧拉公式
e^(ix)=(cos x+isin x)
IP解析
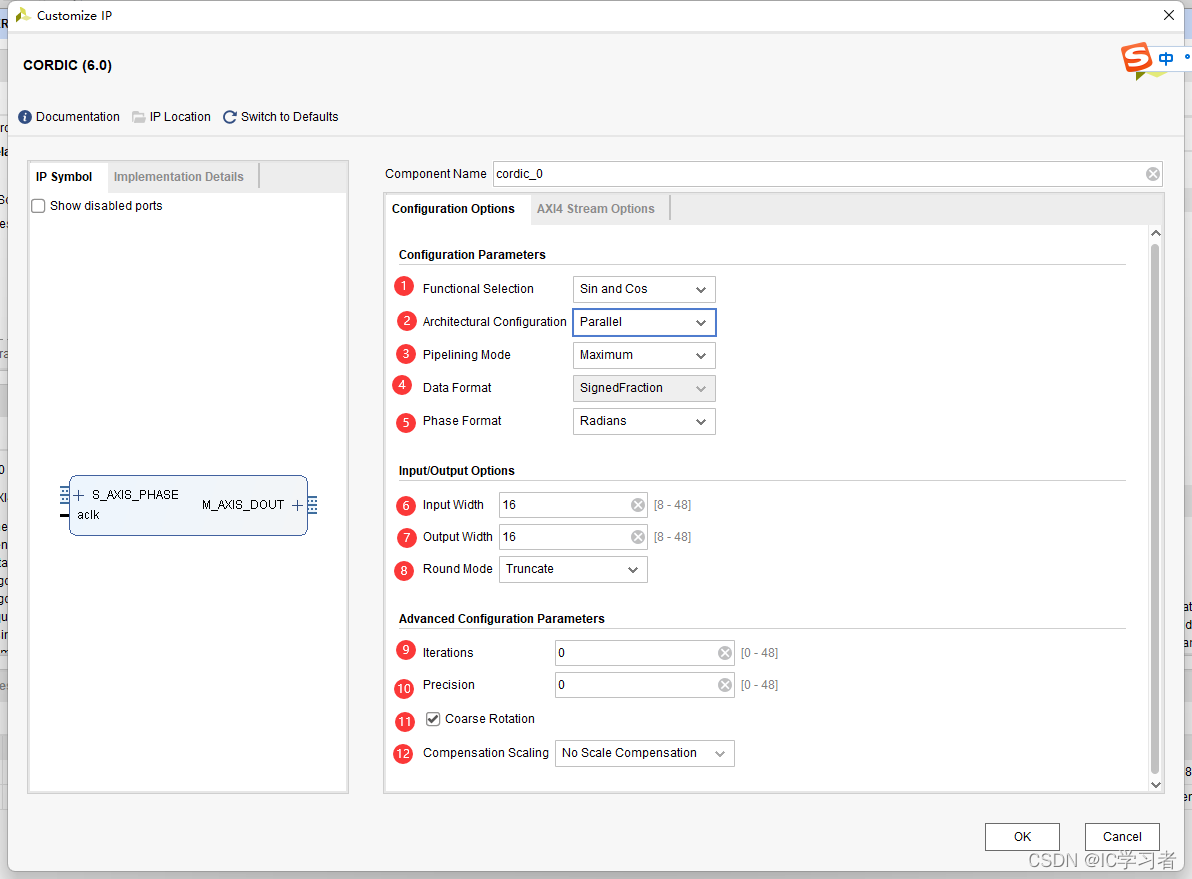
1 选择功能为计算正余弦
2 并行(面积和速度的平衡)
3 流水线模式开到最大(不知道有啥用)
4 有符号小数(整数宽度为2(里面应该包含了一位符号位))
这个选项是默认的,而且我们用的是相位而不是坐标对,可以忽略这个选项
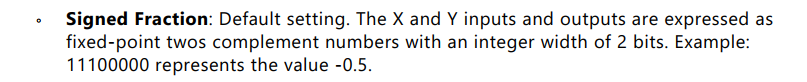
5 相位格式(以弧度为单位还是以pi为单位,1位符号位,2位整数位和N-3位小数位的补码)

不同的格式对应着不同的输入范围,


6 输入宽度(按需配置)
7 输出宽度(建议与输入宽度保持一致)


输入时为2qn,输出时为1qn
8 取整模式(这里计算的是小数,私以为取整模式不重要)
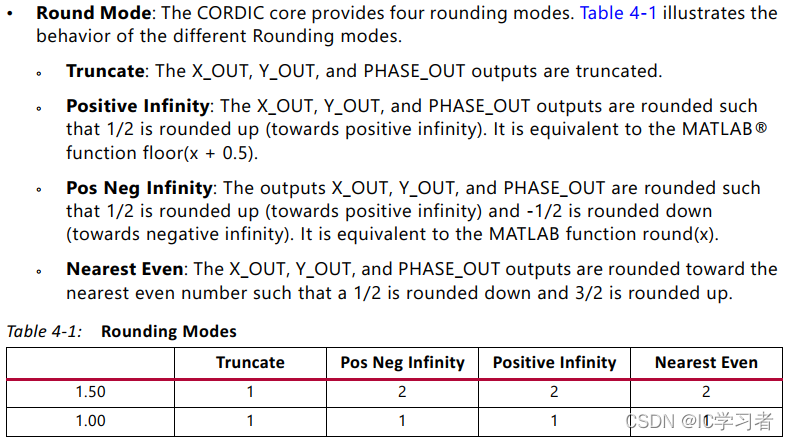
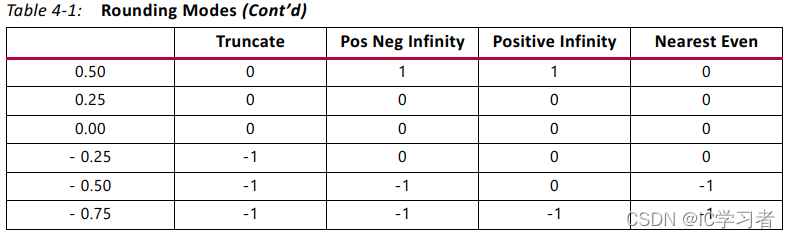
9 迭代次数(设置为0,自动确认)
10 精度(设置为0,自动确认)
11 Coarse Rotation 是否将输入范围从第一象限(-Pi/4 to + Pi/4)扩大到整个圈
12 补偿比例 sin函数下不生效
设置IP
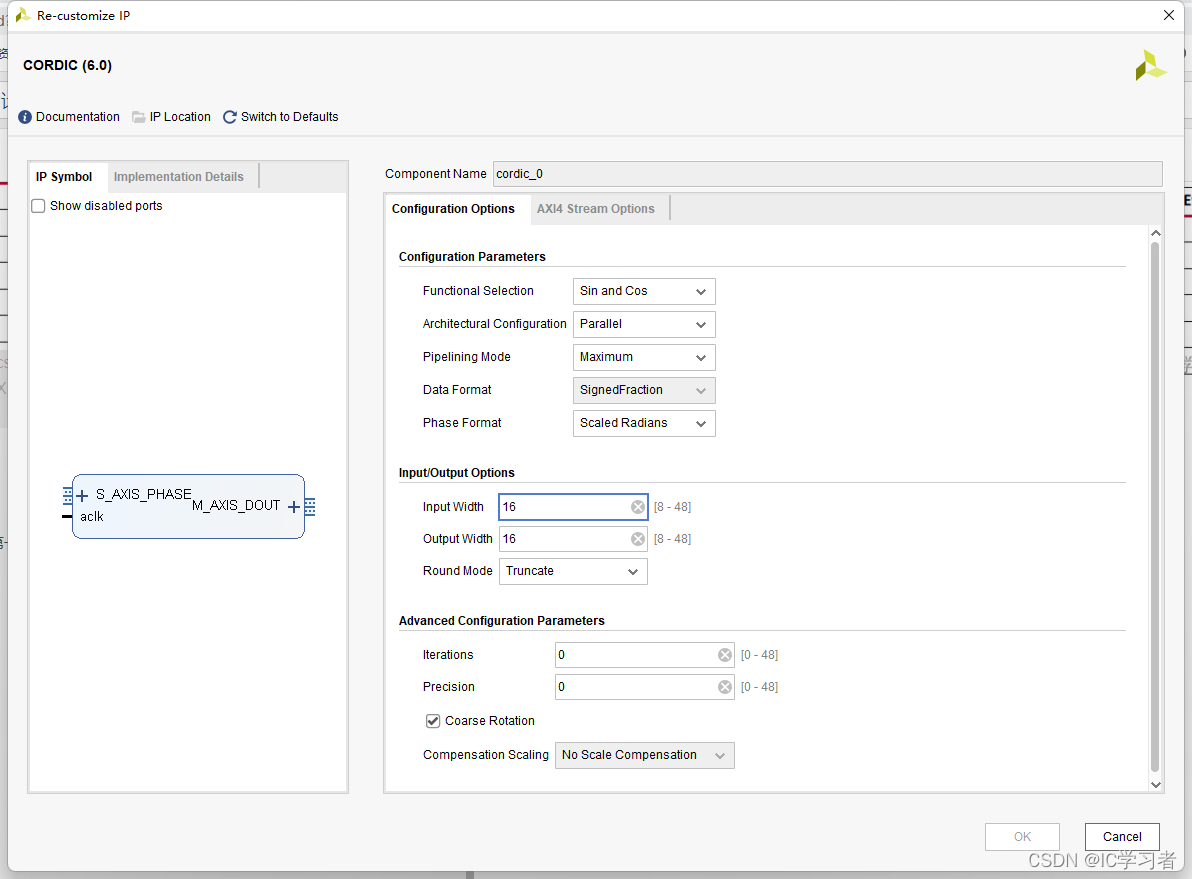
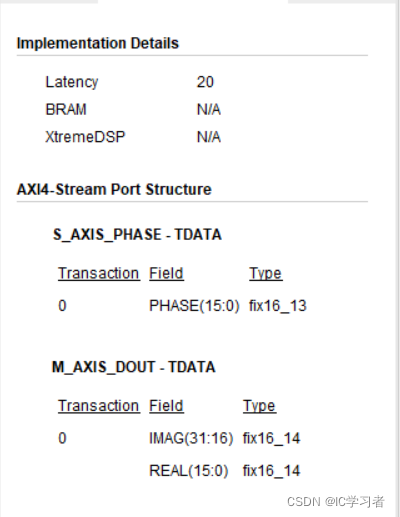
高位表示正弦函数,低位表示余弦函数
HDL Code
module correlation(
input clk,
input rst_n,
input [15:0] phase_in ,
input [ 0:0] phase_vld
);
wire [15:0] sinx;
wire [15:0] cosx;
wire [ 0:0] out_vld;
cordic_0 sin_cos (
.aclk ( clk), // input wire aclk
.s_axis_phase_tvalid ( phase_vld ), // input wire s_axis_phase_tvalid
.s_axis_phase_tdata ( phase_in ), // input wire [15 : 0] s_axis_phase_tdata
.m_axis_dout_tvalid ( out_vld ), // output wire m_axis_dout_tvalid
.m_axis_dout_tdata ( {sinx, cosx} ) // output wire [31 : 0] m_axis_dout_tdata
);
endmodule
Simulation
Code
module tb_correlation;
// correlation Parameters
parameter PERIOD = 10;
// correlation Inputs
reg clk = 0 ;
reg rst_n = 0 ;
reg [15:0] phase_in = 0 ;
reg [ 0:0] phase_vld = 0 ;
// correlation Outputs
initial
begin
forever #(PERIOD/2) clk=~clk;
end
initial
begin
#(PERIOD*2) rst_n = 1;
end
correlation u_correlation (
.clk ( clk ),
.rst_n ( rst_n ),
.phase_in ( phase_in [15:0] ),
.phase_vld ( phase_vld [ 0:0] )
);
initial
begin
#(PERIOD*3) phase_vld = 1'b1;
#(PERIOD*0) phase_in = 16'b1110_0000_0000_0000 ; // -1
#PERIOD phase_in = 16'b1110_1000_0000_0000 ; // -0.75
#PERIOD phase_in = 16'b1111_0000_0000_0000 ; // -0.5
#PERIOD phase_in = 16'b1111_1000_0000_0000 ; // -0.25
#PERIOD phase_in = 16'b0000_0000_0000_0000 ; // 0
#PERIOD phase_in = 16'b0000_1000_0000_0000 ; // 0.25
#PERIOD phase_in = 16'b0001_0000_0000_0000 ; // 0.5
#PERIOD phase_in = 16'b0001_1000_0000_0000 ; // 0.75
#PERIOD phase_in = 16'b0010_0000_0000_0000 ; // 1
#PERIOD phase_vld = 1'b0 ;
#(PERIOD*30)
$finish;
end
endmodule
仿真
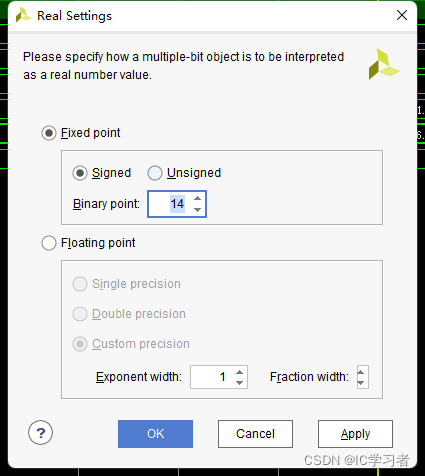
设置输入输出格式
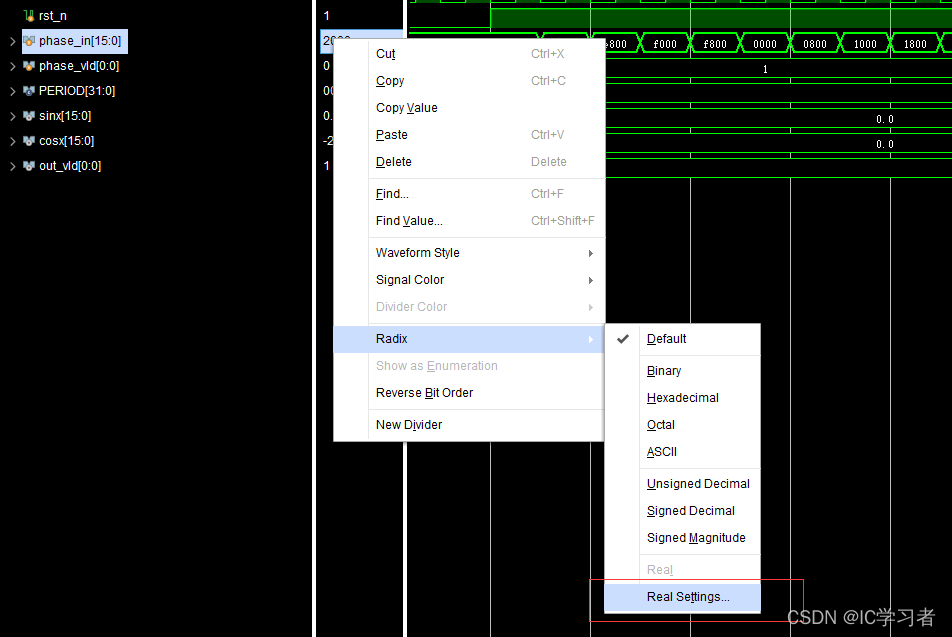
输入格式,有符号,13位小数位
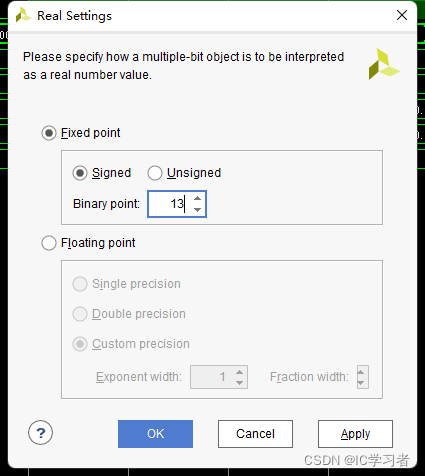
输出格式
仿真结果

reference
pg105
