[网络协议]项目实训八

树形解码器的decoder部分

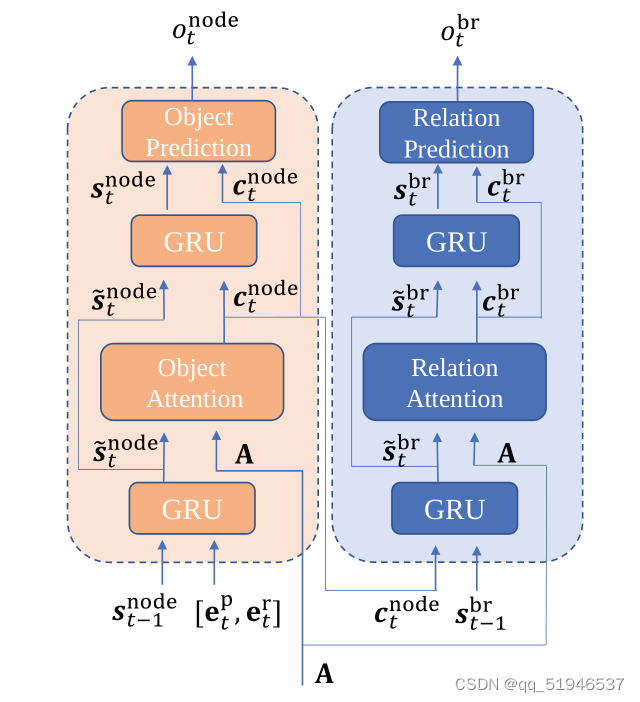
在解码器的每个解码步骤中，树解码器需要预测当前子节点的信息，包括子节点和子节点的分支，节点的分支表示节点与子节点之间的空间关系。我们可以通过节点类别和分支来逐步构建一棵数学树。如下图所示，为了解耦分类和空间关系预测，我们在解码器中设计了两个模块：节点分类模块和分支预测模块。

节点类模块

节点类模块主要包括两个GRU，一个注意力机制和一个分类器，我们首先使用两个嵌入层去获得父节点$p_t$高维的特征向量${\mathbf{e}}_t^{\mathrm{p}}$和${\mathbf{e}}_t^{\mathrm{r}}$以及其空间关系$r_t$。节点解码器${\mathbf{s}}_{t?1}^{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}$的先前隐藏状态被视为${\mathbf{G}\mathbf{R}\mathbf{U}}_1^{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}$层的先前隐藏状态。父节点的嵌入层${\mathbf{e}}_t^{\mathrm{p}}$和空间关系节点的嵌入层${\mathbf{e}}_t^{\mathrm{r}}$一起作为${\mathbf{G}\mathbf{R}\mathbf{U}}_1^{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}$的输入，然后就可以得到${\mathbf{G}\mathbf{R}\mathbf{U}}_1^{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}$的当前隐藏状态${\mathbf{S}}_t^{\text{node?}}$。
$${\mathbf{e}}_t^{\mathrm{p}}={\mathrm{Emd}}_{\text{node?}}\left(p_t\right)$$$${\mathbf{e}}_t^{\mathrm{r}}={\mathrm{E}\mathrm{m}\mathrm{d}}_{\mathrm{r}\mathrm{e}}\left(r_t\right)$$$${\mathbf{s}}_t^{\text{node?}}={\mathrm{GRU}}_1^{\text{node?}}\left(\left[{\mathbf{e}}_t^{\mathrm{p}},{\mathbf{e}}_t^{\mathrm{r}}\right],{\mathbf{s}}_{t?1}^{\text{node?}}\right)$$
然后，节点注意力机制模块$f_{\text{att?}}^{\text{node?}}$被用来在特征映射A上的注意可能性${\alpha }_t^{\text{node?}}$，通过计算在A上的权重之和来获得节点上下文向量${\mathbf{c}}_t^{\text{node?}}$，这里使用${\mathbf{S}}_t^{\text{node?}}$作为query并且A作为key和value。
$${\mathbf{\alpha }}_t^{\text{node?}}=f_{\mathrm{a}\mathrm{t}\mathrm{t}}^{\text{node?}}\left(\mathbf{A},{\mathbf{s}}_t^{\text{node?}}\right)$$$${\mathbf{c}}_t^{\text{node?}}=\sum {\alpha }_{ti}^{\text{node?}}{\mathbf{a}}_i$$
函数$f_{\text{att?}}^{\text{node?}}$如下：
$${\mathbf{F}}^{\text{node?}}={\mathbf{Q}}^{\text{node?}}?\sum _{l=1}^{t?1}{\mathbf{\alpha }}_l^{\text{node?}}$$$$e_{ti}^{\text{node?}}=V_{\text{node?}}^{\mathrm{T}}\tanh \left({\mathbf{W}}_{\text{att?}}^{\text{node?}}{\tilde{\mathbf{s}}}_t^{\text{node?}}+{\mathbf{U}}_{\text{att?}}^{\text{node?}}{\mathbf{a}}_i+{\hat{\mathbf{U}}}_{\mathrm{F}}^{\text{node?}}{\mathbf{f}}_i^{\text{node?}}\right)$$$${\alpha }_{ti}^{\text{node?}}=\frac{\exp \left(e_{ti}^{\text{node?}}\right)}{{\sum }_k\exp \left(e_{tk}^{\text{node?}}\right)}$$
${\alpha }_{ti}^{\text{node?}}$表示第t步的第i个元素的节点的可能性，$e_{ti}^{\text{node?}}$表示第i步的输出，${\mathbf{f}}_i^{\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}}$表示函数${\mathbf{F}}^{\text{node?}}$的第i个元素，这是以前的注意模块，为了避免过度解析或者解析不足的问题，其余为学习参数。
接着，使用${\mathbf{c}}_t^{\text{node?}}$和${\mathbf{s}}_t^{\text{node?}}$作为${\mathbf{G}\mathbf{R}\mathbf{U}}_2^{\text{node?}}$的输入来计算预测模块隐藏状态${\mathbf{s}}_t^{\text{node?}}$
$${\mathbf{s}}_t^{\text{node?}}={\mathrm{GRU}}_2^{\text{node?}}\left({\mathbf{c}}_t^{\text{node?}},{\mathbf{s}}_t^{\text{node?}}\right)$$最后通过父节点${\mathbf{e}}_t^{\text{p}}$，与父节点的关系${\mathbf{e}}_t^{\text{r}}$，节点的隐藏状态${\mathbf{s}}_t^{\text{node?}}$以及上下文向量${\mathbf{c}}_t^{\text{node?}}$的聚合来计算预测节点${\mathbf{o}}_t^{\text{node?}}$的可能性：$${\mathbf{h}}_t^{\text{node?}}=\mathrm{maxout}\left({\mathbf{W}}_1^{\text{node?}}\left[{\mathbf{e}}_t^{\mathrm{p}},{\mathbf{e}}_t^{\mathrm{r}},{\mathbf{s}}_t^{\text{node?}},{\mathbf{c}}_t^{\text{node?}}\right]\right)$$$${\mathbf{o}}_t^{\text{node?}}=\mathrm{softmax}\left({\mathbf{W}}_2^{\text{node?}}{\mathbf{h}}_t^{\text{node?}}\right)$$其中W参数为学习参数。
我们使用cross-entropy函数来计算分类的损失函数$${\mathcal{L}}_{\text{node?}}=?\sum \log {\mathbf{o}}_t^{\text{node?}}?{\mathbf{n}}_t$$${\mathbf{n}}_t$表示第t步节点真实值的独热向量。

上周只进行了模块分析和一部分代码的编写，这周将完成者模块代码的编写。

2022深度学习开发者峰会

5月20日13:00让我们相聚云端，共襄盛会！