文章目录
加密方式
对称加密
- 发送和接收方使用统一的秘钥
- 存在秘钥分发问题
- 加密简单,但是安全性略低
AES 加密(标准)

ECB 电子密码本
- 参考之前的文章
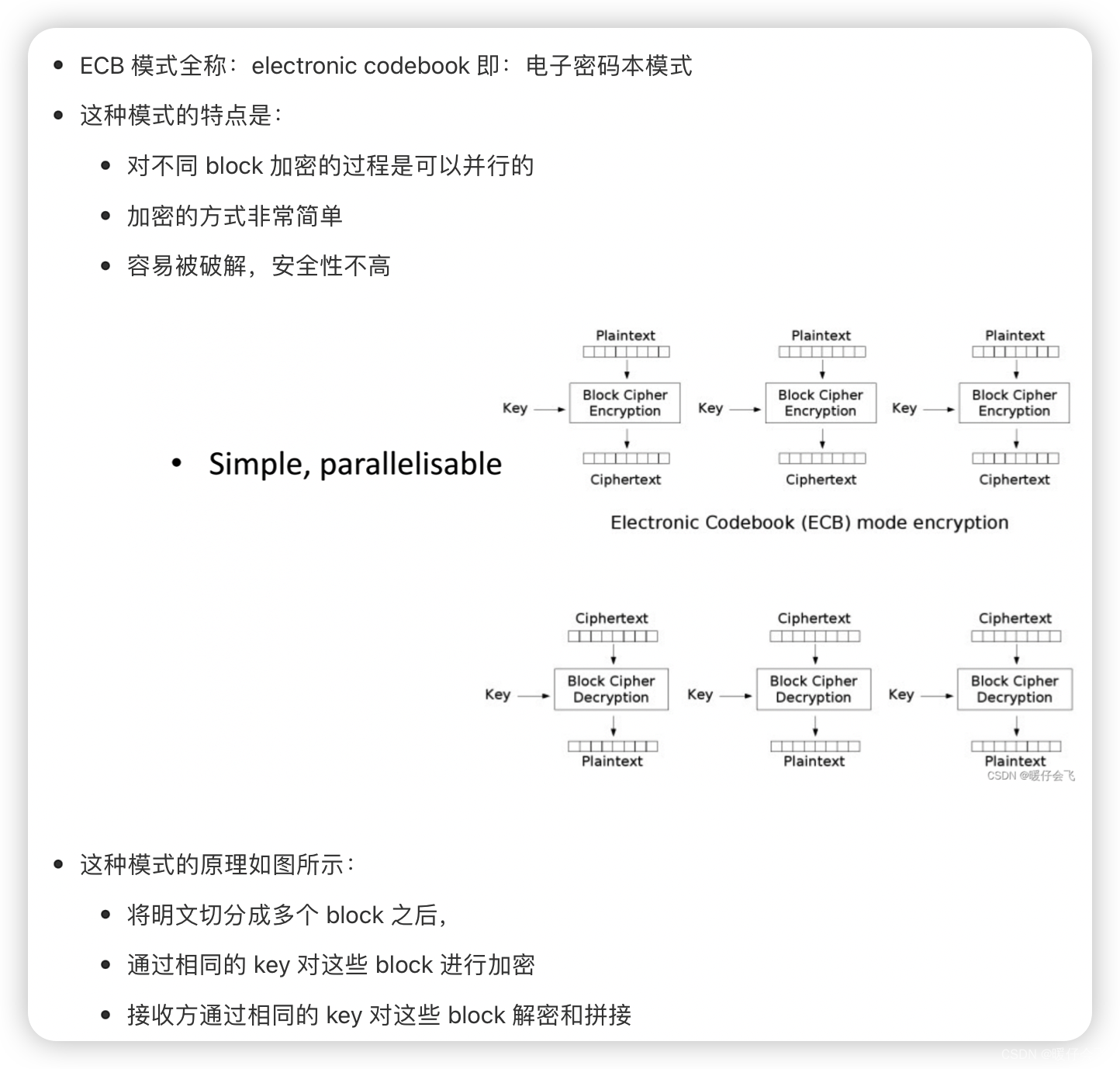

- 因为都是用同一个 key 加密所有的 block,因此如果一个被破译,所有的 block 都可以被破译
- 即便 key 不被破解,那么相同的明文就会有相同的密文模式
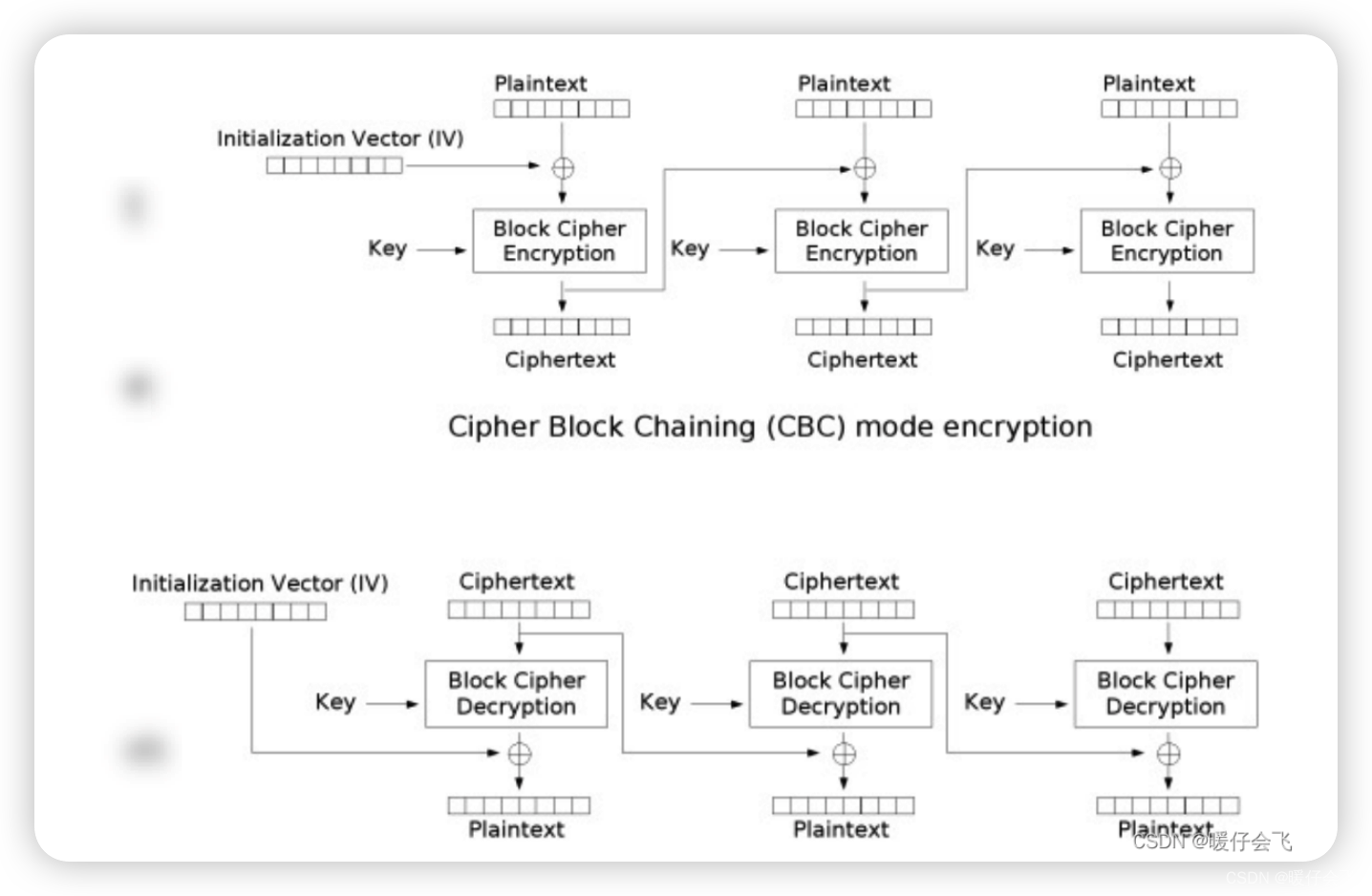
CBC cipher block chaining
- IV 可以公开,但必须随机且不可重用
- 加密不可并行,必须顺序加密
- 解密可以并行
- 丢失密文的影响小,丢失一个 block 或者 IV 最多影响 2 个 block


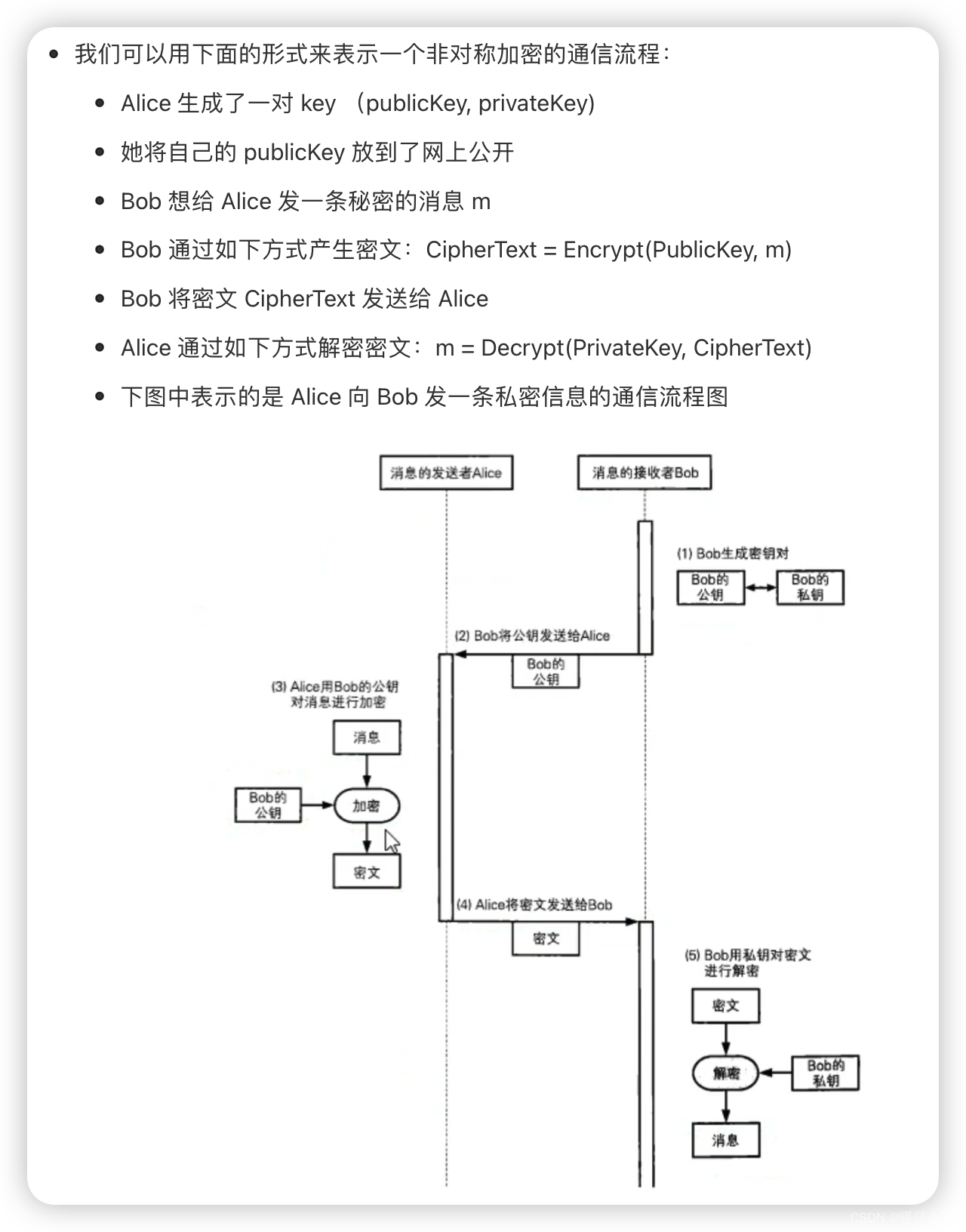
非对称加密
- 使用公钥私钥对
- 加密的复杂度高,一般是对称加密的 20-100 倍
- 更加安全,但是不适合处理大规模数据
对称加密 vs 非对称加密

TLS 的 Handshake 协议(结合对称和非对称加密的方式)
- 其原理就是通过非对称的方式交换 公共秘钥,完成秘钥的分发
- 然后通过对称加密的方式操作大规模的加密信息

数字签名
-
数字签名通常 可以用来验证信息的完整性和发信人的身份
-
数字签名的过程与加密的过程相反,使用 私钥对明文进行签名,接收方使用公钥来验证
-
假设明文是 m,A 与 B 进行通信,A 将 m 发给 B的时候发送了两个部分:
- m 明文本身
- 用 A 的私钥对 m 签名后的内容 Private(m) P_m
-
这样 B 收到信息之后只要能用 A 的公钥计算 P_m 只要能够得到 m 就证明发信人的身份是 A
-
但是如果出现了大段的内容,采用这种方式的代价就很大,因此我们需要使用一个 摘要 H(m) 来代替 m 本身,A 只需要对 H(m) 签名,就可以得到签名 m 一样的效果;这个过程中采用的算法是散列算法:
- A 首先将 m 通过散列函数获得散列值 H(m),然后使用 A 的私钥对 H(m)进行签名,然后将 m 和 P_(H(m)) 一起发送给 B
- B 接收之后通过公钥得到 H(m) 然后对 m 采用相同的散列算法如果得到的结果也是同 H(m) 值一样,就说明信息是完整的而且确实是 A 发出的
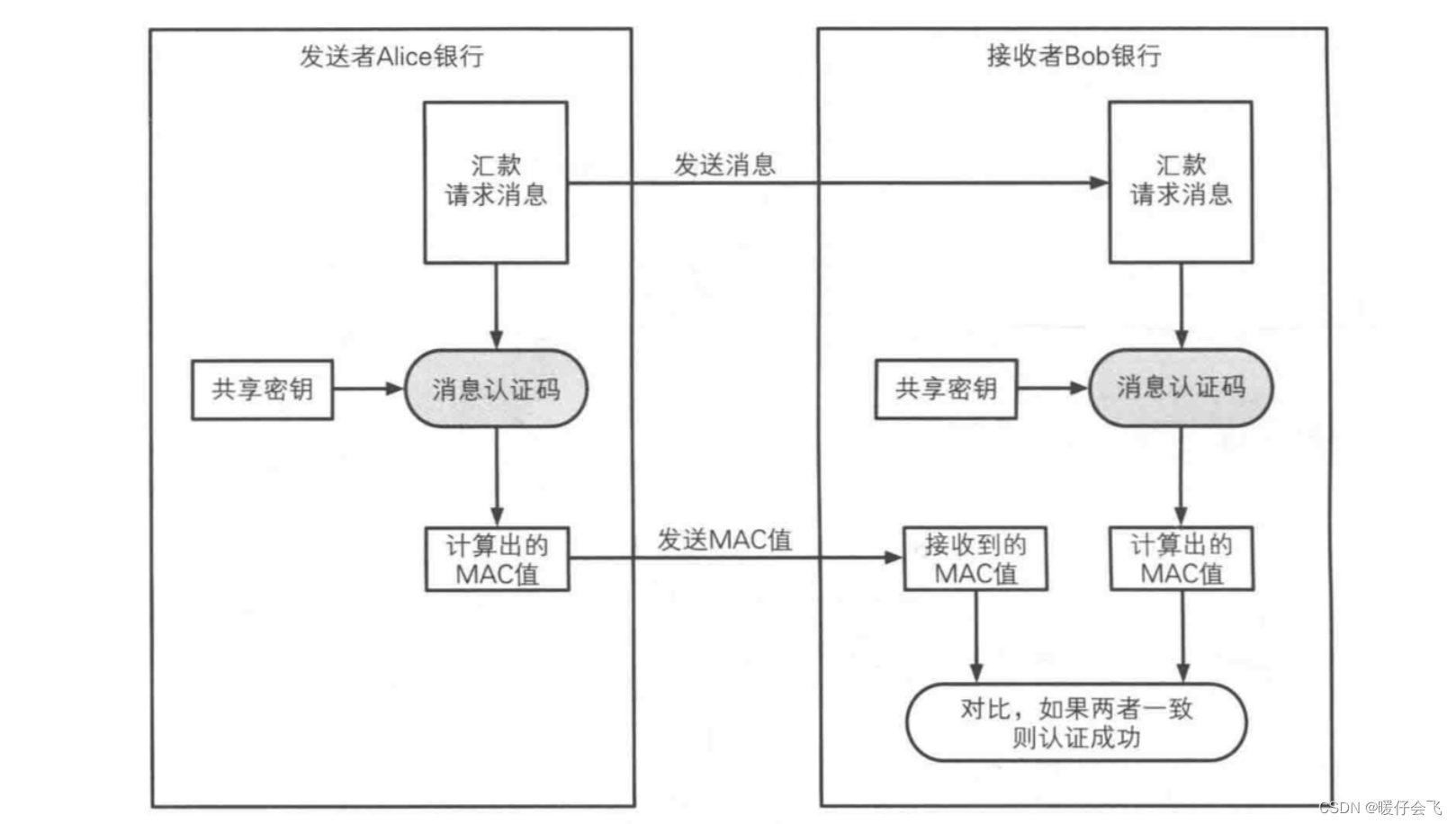
消息认证码 MAC
- MAC 是一种采用对称方式来 保证传输信息完整性和身份认证 的方式
- 消息认证码在传输的过程中也采用了 散列算法,但不是对明文 m 进行单独的散列运算,而是对 m+secret key 共同进行散列运算,这样处理的信息掺杂了秘钥信息,因此既可以保证信息是完整的,也可以对身份进行认证。

Diffie-Hellman Key Exchange & MITM

- 首先选择一个很大的素数p(prime) 和一个 g(generator);
- 然后双方A, B 分别各选一个随机数
x
,
y
x, y
x,y
- 第一步,双方分别求算 a = g x m o d ? p a=g^xmod ~p a=gxmod?p 和 b = g y m o d ? p b=g^y mod ~p b=gymod?p 可以分别得到各自的结果;然后将这个结果发送给对方
- A 拿到 B 发来的 b b b,B 也拿到了 A 发来的 a a a
- 然后 A 再计算 b x m o d ? p b^x mod~p bxmod?p,B 计算 a y m o d ? p a^y mod ~p aymod?p
- 通过这一步的计算 A,B 就会得到同一个值,这个值就是他们对称加密使用的 “共同秘钥”
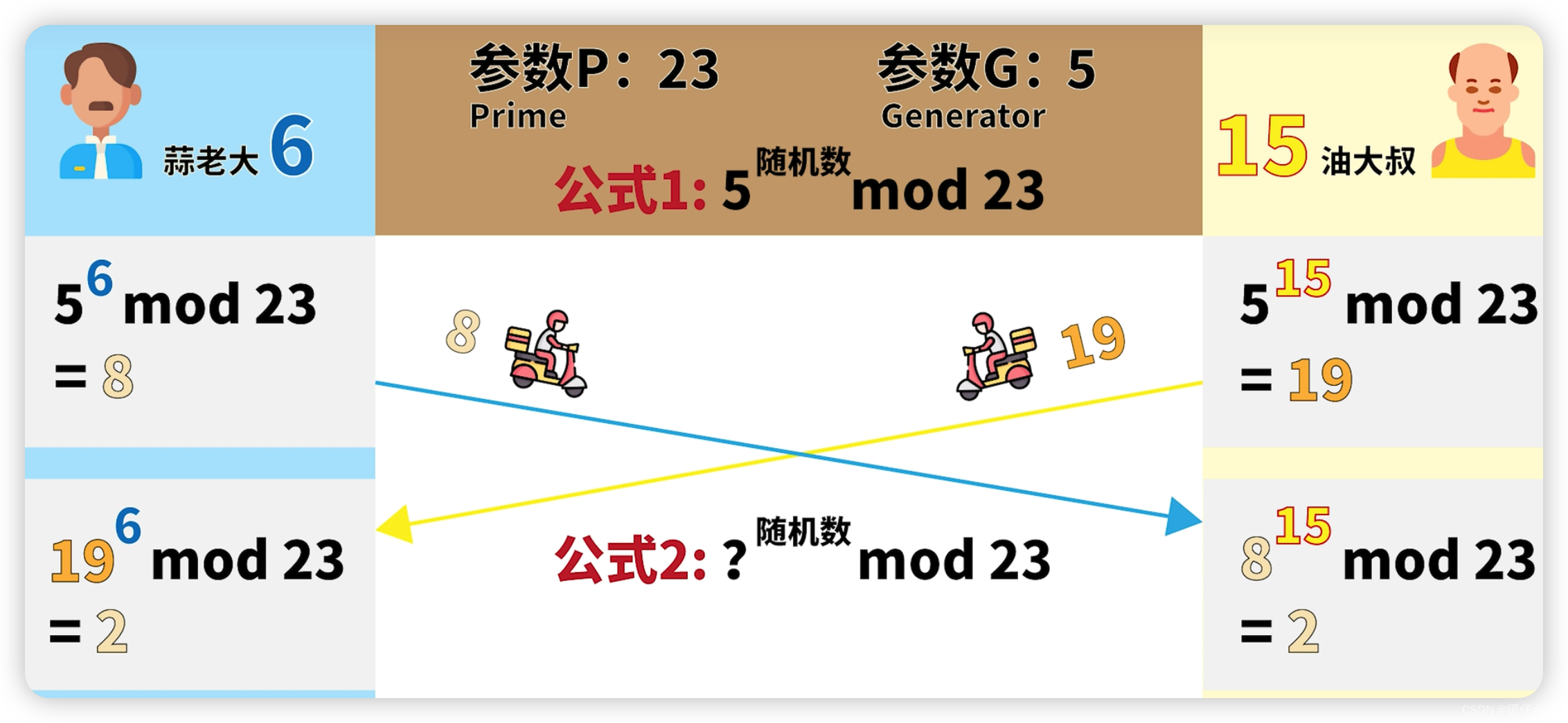
- 因此 Diffie-Hellman 算法本质上是通过双方指定随机数之后,交换第一次运算的结果然后根据随机数和交换得来的结果最终算出共同的秘钥
- 在上图的例子中,蒜老大的随机数是 6,油大叔的随机数是 15,p=23,generator=5,然后最后算出的公共秘钥是 2
通信安全的预期特性
- 通信安全的要求是:可信性 confidentially; 认证性 authentication;完整性integrity
- 对称和非对称加密保证了通信的可信性,即信息只有通信双方可见
- 数字签名可以保证认证性,因为能够确认发信方的身份
- 数字签名和散列函数都能够保证信息的完整性,即信息在发送过程中不被篡改和损坏