《密码编码学与网络安全》William Stalling著 — 学习笔记(一)—传统密码+经典对称加密算法+经典公钥密码算法+密码学Hash函数—知识点速过
写在前面
最近因为学习的需要初步接触网络安全方向,阅读的书是William Stalling著的《密码编码学与网络安全(第六版)》。由于本科期间是计科的Web应用开发方向,没有系统接触过网络安全方面的课程,所以从密码学入门。做个学习笔记方便后期复习,同时也分享给大家。由于本人能力有限肯定会有总结和理解不到位的地方,甚至有的地方会有错误(当然目前我没发现…)我若日后发现也会及时更新修改,所以希望各位辩证的学习,不要尽信书。阅读的参考书封面如图所示。

1. 传统密码
1.1 Casear密码
简单的由字母表中循环后推k位。
穷举攻击即可解决 密钥空间为25
1.2 单表代替密码
给出一张一一映射的密码表。
明文的任一置换。对长度为n的明文,密钥空间为n!
不足之处:带有原始字母使用频率特征,仍然可以通过统计学手段进行密码的破解
改进:进一步的减小这种频率特性。
1.3 Playfair密码(多字母代替密码)
密钥词: i am BUAAer
明文:hello world
| I(J) | A | M | B | U |
| E | R | C | D | F |
| G | H | K | L | N |
| O | P | Q | S | T |
| V | W | X | Y | Z |
step1:配对。he lx lo wo rl dx
step2:同行循环用右字母代。
step3:同列循环用下字母代。
step4: ch1(a,b),ch2(c,d) cipher_ch1(a,d),cipher_ch2=(c,b)
不足: 频率分析难度上升,但是原文结构仍然存在
1.4 Hill密码
AA-1=A-1A=E
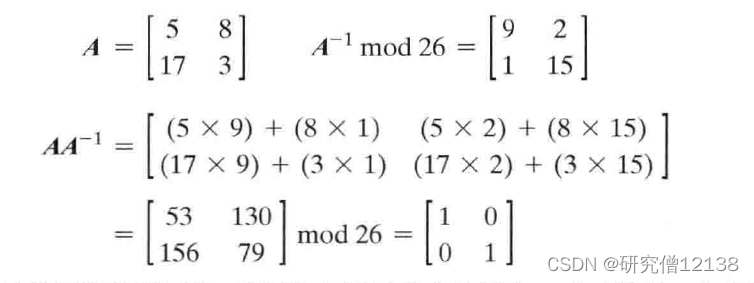
由m个线性等式决定,将m个明文字母替换成m个密文字母
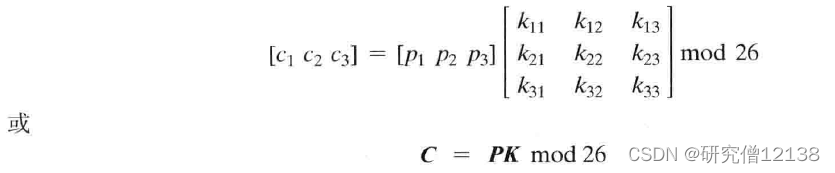
Hill密码系统:
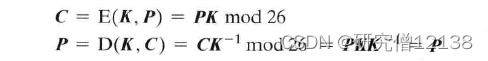
完全屏蔽了单字母的频率特性,且加密密钥矩阵越大,隐藏的频率信息越多
缺点: 易被已知明文攻击破解
设名密文对分别为X,Y,K=X-1Y
1.5 多表代替加密
明文消息中采用不同的单表替代。
1.5.1 Vigenere密码(维吉尼亚密码)
相当与一份26个Caesar密码代替表组成。
密文字母=(明文字母+密钥字母) mod 26
屏蔽了字母出现的频率信息,但是Vigenere密码频率分布特征仍然能够被分析出。
密钥一般为一个密钥词的重复(破译重点:判断密钥词的长度)
–> 计算重复密文序列间距的公因子,猜测出密钥词长度。
1.5.2 Vernam密码(弗纳姆密码)
流密码典型代表 一次一密典型代表
明文二进制与秘密钥二进制按位进行异或运算
选用周期大的循环密钥
有足够密文和明文序列,仍然可以破解
1.6 一次一密-不可攻破
使用穷举法可以分析出大量的可读明文,因为无法唯一确定原始明文是哪一条。
应用难点:产生大规模随机密钥困难, 密钥分配管理困难
1.7 置换技术
- 栅栏技术
- 写成矩阵,按列读出,列顺序为密钥
进一步的:多次加密
1.8 转轮机
图灵在二战时期破译的德军恩格玛机,改变了二战的走向。
转轮机的构造如下图:

破解困难:轮转方向不可知,连线顺序不可知。
转轮越多,密码系统就越难破解
1.9 隐写术
例子:藏头诗等,不可见墨水(比如谍战片中常看到的用水泼上去才能看到字等),紫外线光下展现。
2. 经典对称加密算法
Feistel密码强度:迭代轮数,函数F,密钥使用算法
密码根据加密的处理方式可以分为 ▲分组密码 流密码,本文主要讲述分组密码。
分组密码的工作模式
电码本模式
密文分组链接
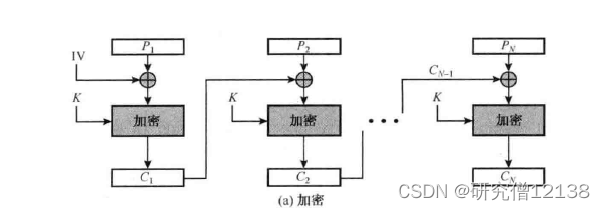
密文反馈模式
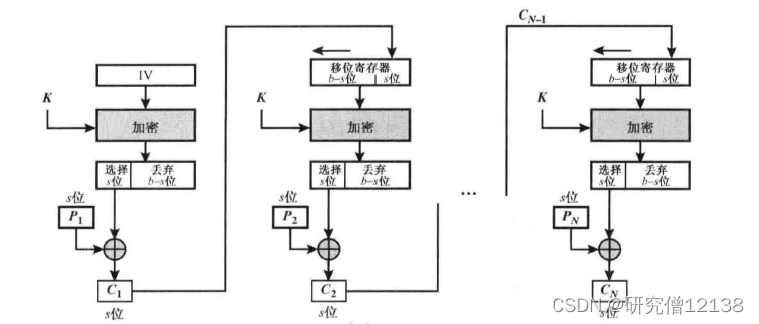
输出反馈模式
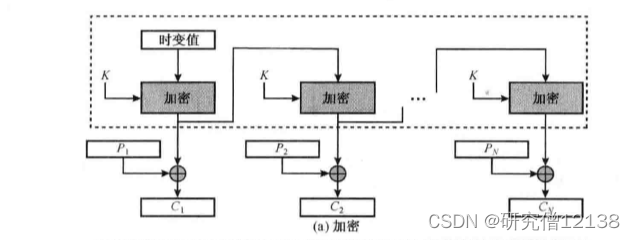
计数器模式

了解工作模式的好处是 :即使使用相同的加密算法,在不同的工作模式下输出的密文会不相同。
2.1 DES (数据加密标准 Data Encryption Standard)
DES加密过程
64位密钥(56bit可用,8bit作为校验位,再从56bit中以一定方式选取48bit)
step1:初始置换(一个单表替换)
64bit分为两32bit进行处理
step2:16轮计算
轮函数计算:
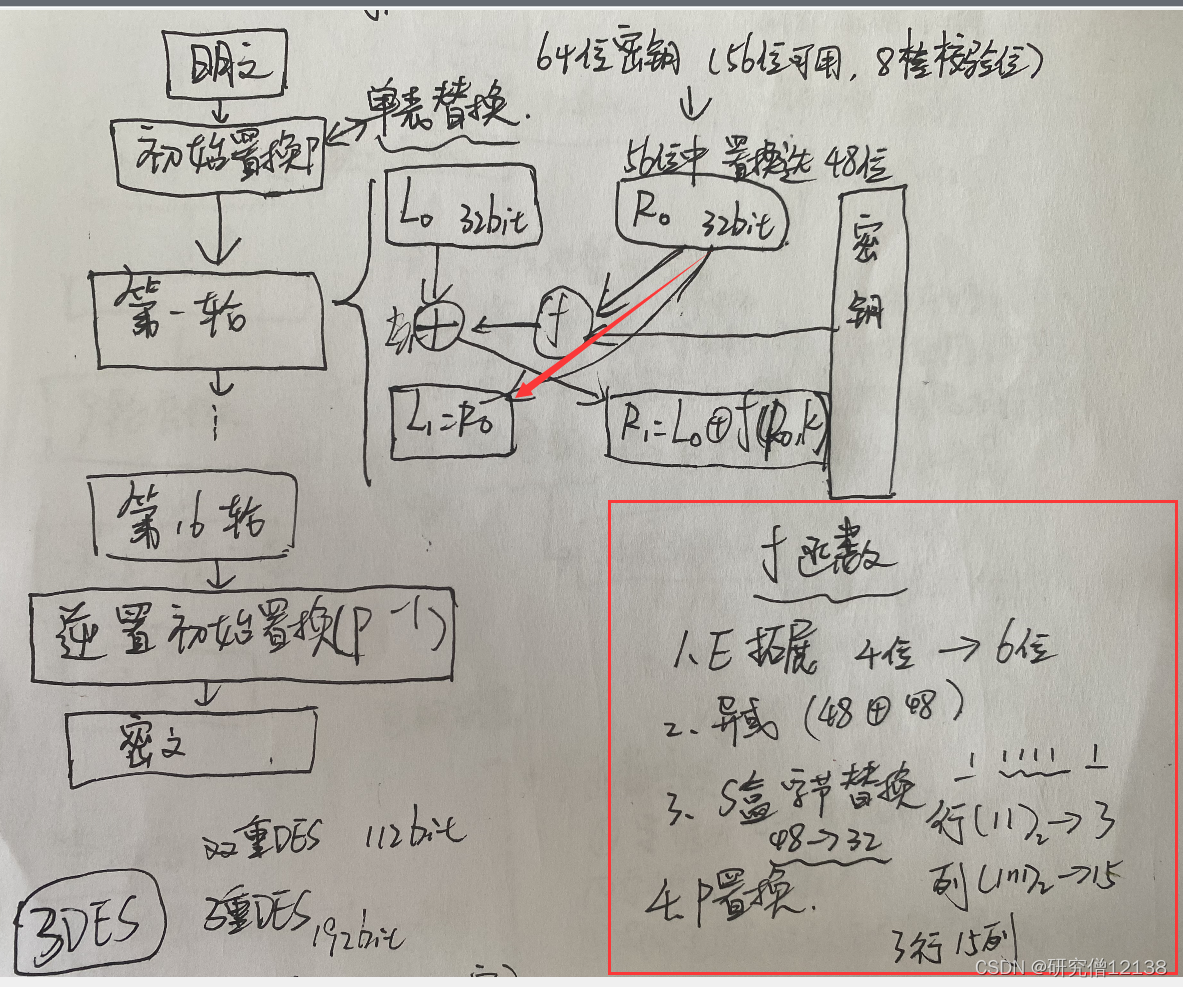 step3:逆置初始变换
step3:逆置初始变换
step4:得到密文
密码强度:256 = 7.2*1016
3DES
DES的一个变型(加密、解密、加密)
若关于这没有看懂的同学,我建议查看这个视频。我是通过这个视频看懂的,UP主十分强!!!
DES加密详细流程-视频讲解
2.2 AES (高级加密标准 Advanced Encryption Standard)
(Rijndael算法)
按照密钥长度,分为不同AES。16字节、24字节、32字节(AES-128、AES-192、AES-256)
但是其加密过程都是一脉相承。我们以AES-128为例子详细解释。
AES-128
将密钥16字节,写为写成4*4矩阵,然后按照下列流程图进行数据加密。

轮函数
-
字节代替(S-Box)
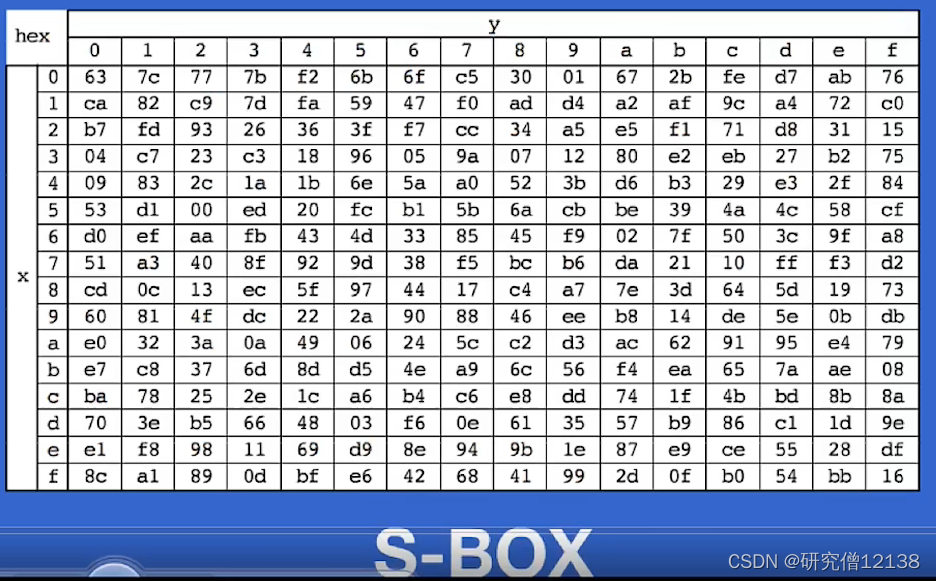
-
行位移(简单的置换)
向左循环移动字节 -
列混合:在有限域GF(2^8)上的计算,即有限域上的乘法、加法。

我们在前面学到,任何的乘法都可以转为加法来做。如果A+A=2A
在二进制中,任何一个数又可以表示为八个数串相异或组成,
0x01:0000 0001
0x02:0000 0010
0x04:0000 0100
…
0x40:0100 0000
0x80:1000 0000
而计算机中一个数乘这八个数其实都代表左移相应的位数,有利于硬件实现。

-
轮密钥加(其实就是一个简单的vernam密码)

轮密钥生成 (密钥扩展)分为两种情况
Ⅰ.Wi,i是4的倍数: W[i]=W[i-4]XOR T( W[i-1] )
Ⅱ.Wi,i不是4的倍数:W[i]=W[i-4]XOR W[i-1]

最终轮不进行列混合
若关于这没有看懂的同学,我还是建议查看这个UP主的视频
AES详细加密流程(包含轮密钥生成)-视频讲解
3. 经典公钥密码算法
3.1 RSA算法
RSA算法由麻省理工的三位大神 M.Rivest; A.Shamir;L.Adlman发明,并用他们的名字首字母命名。
基于数学难题:大整数的因数分解在计算上不可行。
单向陷门函数-定义:

可变参数称为陷门信息
在我的理解中,所有公钥密码设计其实都是一个单向陷门函数,正向计算很容易(类比于我们加密密文,计算密文十分容易)。若是你有陷门信息(比如已知的公/私钥),可以很容易的反向推导出原文(解密信息)。若是没有,则很难反向推导出原文(解密信息获得明文)
RSA算法加密过程:
step1:选择一对不相等,足够大的质数p,q。
step2: n =pq
step3:计算n的欧拉函数 ( f(n)=(p-1)(q-1) )
step4:选出一个与n互质的整数e
step5:计算出e对与f(n)的模反元素d–>满足ed mod f(n)=1 ( f(n)为n的欧拉函数 )
(d为e对f(n)的逆元)模反元素:如果两个整数e和f(n)互质,那么一定可以找到一个整数d
使得,ed-1被f(n)整除 ( 或ed mod f(n) = 1 )
此时,d叫做e的模反元素
step6:公钥KU=(e,n)
step7:私钥KP=(d,n)
明文M 加密 Me mod n = C
密文C 解密 Cd mod n = M
(可以使用欧拉定理证明)
3.2 Diffie-Hellman密钥交换算法(迪菲-赫尔曼密钥交换算法)
基于数学难题: 一般有限域上离散对数的难解性

不能抵抗中间人攻击
3.3 EIGamal加密算法
基于DH密钥交换算法的非对称加密算法,使用一次性密钥K。
加密过程:
- 公开全局变量
q 素数
a a<q,且a是q的素根- Alice生成密钥
选择私钥XA XA<q-1
计算YA YA=aXA mod q
公开密钥 {a,q,Ya}- Bob用Alice公钥加密
明文 M<q
随机选择整数k, k<q
计算一次密钥K K=(YA)k mod q
计算C1 C1=ak mod q
计算C2 C2 = KM mod q
密文 (C1,C2)- Alice收到密文使用私钥解密
计算一次性密钥K
K=(C1)XA mod q
计算明文M
M=(C2*K-1) mod q
3.4 ECC(椭圆曲线密码)
椭圆曲线:形如 y2=X3+aX+b (4a3+27b2 ≠0,保证曲线上任意一点均存在切线)关于X对称。
我的理解:
椭圆曲线的加法与我们日常使用的加法系统不同。如图中所示,A+B=C的结果为过A、B直线与椭圆曲线相交的另外一点关于X轴对称的点。
椭圆曲线的乘法可以转化为加法理解,例:B=2A=A+A, C=3A=A+B…以此类推。B=A+A在图中的意义就是过A点做切线与椭圆曲线相交的另外一点关于X轴对称的点。
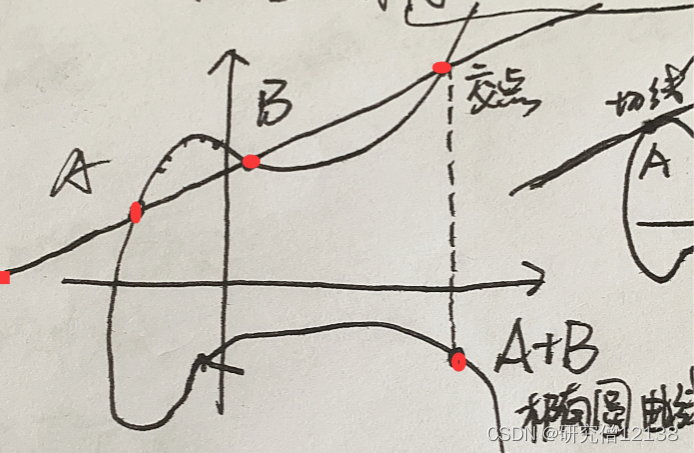
连续域上的椭圆曲线一般不能用来密码学中直接使用,我们一般使用有限域上的离散的点。
有限域上的椭圆曲线:
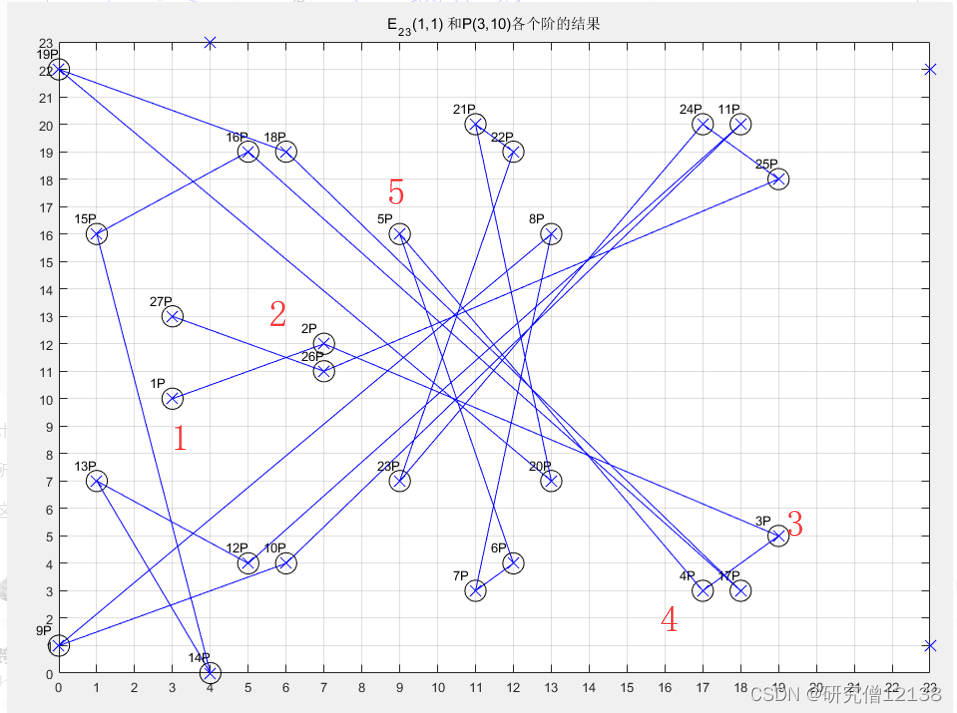
可以看到2P+P=3P 3P+P=4P但是各个P的倍数的点在坐标系中显得杂乱无章。但是越杂乱对攻击者来说就是噩梦但是对密码系统得使用者而言便越安全。
椭圆曲线密码基于: 椭圆曲线离散对数问题(Elliptic Curve Discrete Logarithm Problem)
k=log p(Q),k为以P为底Q的椭圆曲线离散对数
设椭圆曲线上两个点P、Q,k为整数
Q=kP
P称为基点,k为私钥,Q为公钥,当质数k取特别大的时候,穷举出k是非常困难的
有限域上的计算
ECC加密: 选择随机数r,将消息M加密为密文C
密文为一个点对 C(rP,M+rQ)(ps:这里Q为接收方公钥)
ECC解密: 第二个点减去第一个点与B的私钥之积
M+rQ-k(rP)=M+r(kP)-k(rP)=M
4. 密码学Hash函数
4.1 MD5(消息摘要算法 Message Digest Algorithm 5)
用处:密码保护、文件完整性校验、数字签名、文件秒传
输入:任意长度
输出:128bit消息摘要
分组长度:512bit(再分为1632bit的子分组)
迭代次数:164次
每个子分组记为M0、M1、M2…M15,均需进行4次运算FF、GG、HH、II
标准幻数:A=0x01234567 B=0x89abcdef C=0xFEDCBA98 D=76543210
程序中为小端模式:A=0x67452301 …
以512bit为一个分组,进行四轮运算,涉及的均为对初始值的更改,将一个块的输出结果作为下一块的初始值,直到最终一块计算完毕。
F( X ,Y ,Z ) = ( X & Y ) | ( (~X) & Z )
G( X ,Y ,Z ) = ( X & Z ) | ( Y & (~Z) )
H( X ,Y ,Z ) =X ^ Y ^ Z
I( X ,Y ,Z ) =Y ^ ( X | (~Z) )
FF(a ,b ,c ,d ,Mj ,s ,ti)
操作为 a = b + ( (a + F(b,c,d) + Mj + ti) <<< s)
GG(a ,b ,c ,d ,Mj ,s ,ti)
操作为 a = b + ( (a + G(b,c,d) + Mj + ti) <<< s)
HH(a ,b ,c ,d ,Mj ,s ,ti)
操作为 a = b + ( (a + H(b,c,d) + Mj + ti) <<< s)
II(a ,b ,c ,d ,Mj ,s ,ti)
操作为 a = b + ( (a + I(b,c,d) + Mj + ti) <<< s)
ti为常量
- MD5不再安全,但依旧广泛应用
- MD5的攻击
鸽巢原理–>一定会发生碰撞
原像攻击不可行,
穷举攻击 2128 太大了 不可行
第二原像攻击也不可行
我国密码学家王小云院士:碰撞攻击可行,通过碰撞攻击可以达到MD5的解密。
下面是王小云院士的思路(看不懂目前…)
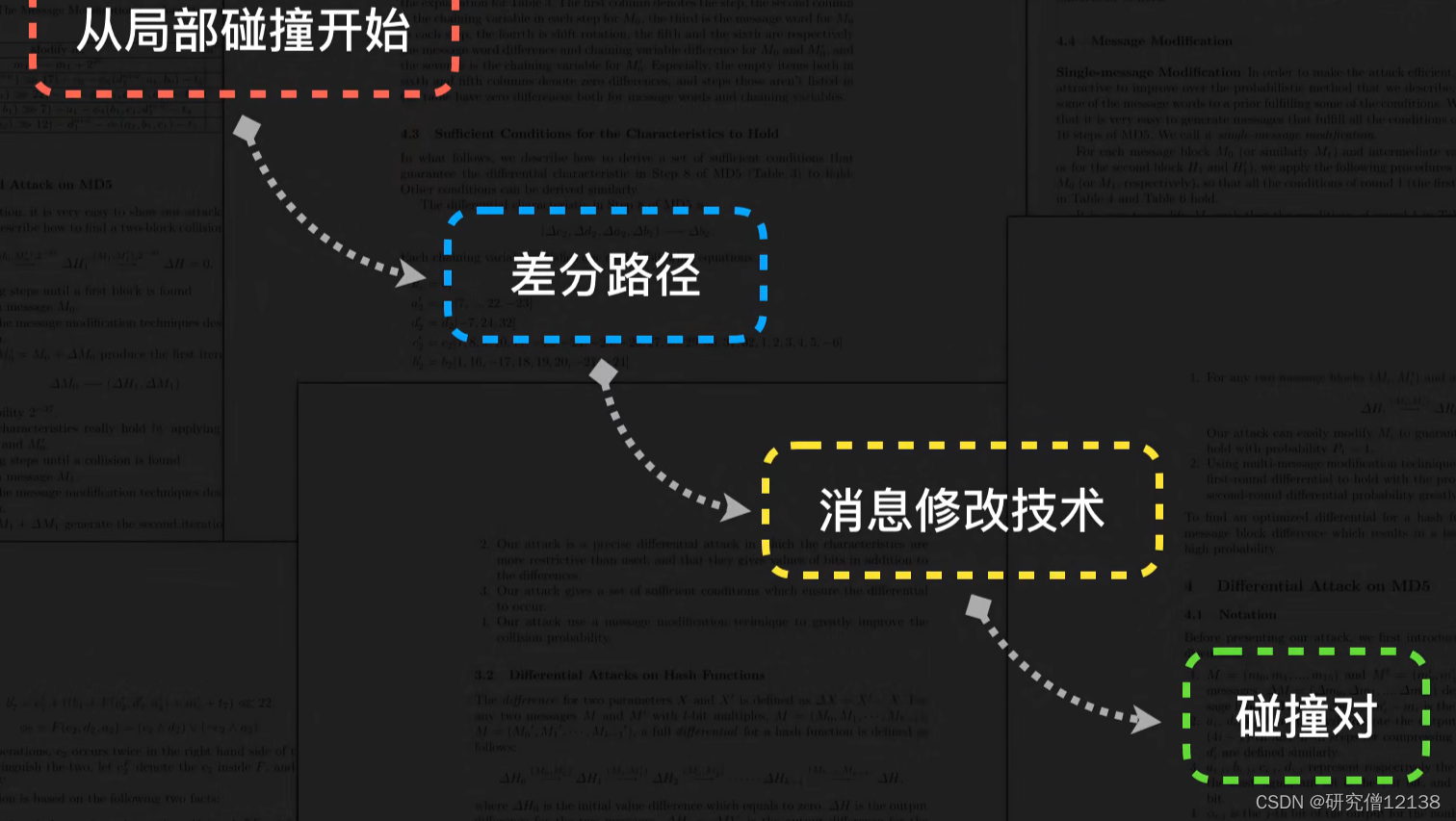
**相同前缀碰撞:文件完整性校验变得危险。**前缀相同,但是通过对后缀的修改,若可以实现MD5值依然相同那么将会是一件危险的事。试把蒙娜丽莎的微笑想象成你要下载的可执行文件。另外一份是恶意文件。通过后缀中某个条件可以出发恶意行为。如果先用正常的软件通过恶意软件检测,再悄悄替换为危险软件,由于这两个软件MD5值相同,恶意软件会被认为是前面检查过的可执行文件。这就给攻击者可趁之机。

选择前缀碰撞:MD5值一样,两个程序完全不同。数字签名比较危险(数字支票金额支付)。
4.2 SHA (安全散列算法 Secure Hash Algorithm)
抗原像攻击
抗第二原像攻击 (抗弱碰撞性)
抗碰撞攻击(抗强碰撞性)
4.2.1 SHA-0
被发现存在缺陷
4.2.2 SHA-1
建立在MD4算法之上
2017年Marc Stevens和Google团队完成了完整轮数的SHA-1的一个实际碰撞攻击,这标志着SHA-1已经彻底不再安全。
输入M: 0<L<2^64
输出:160bit的消息摘要
对每个512数据块进行相应轮数计算、前一分组输出的消息摘要同时也作为后一分组的输入

a=H0 b=H1 c=H2 d=H3 e=H4 -->初始链接变量
轮函数:
For t=0 to 79{
T=ROTL^5(a)+ft(b,c,d)+e+Kt+Wt ch(x,y,z)=(x^y) ⊕(x^z) 0<=t<20
e=d parity(x,y,z)=x ⊕ y ⊕ z 20<=t<40
d=c ft(x,y,z)= (x^y) ⊕(x^z) ⊕(y^z) 40<=t<60
c=ROTL^30(b) parity(x,y,z)=x ⊕ y ⊕ z 60<=t<80
b=a
a=T
}
Kt为给定常量字,
每一轮链接变量为:
a=H0=a+H0’
b=H1=b+H1’
c=H2=c+H2’
d=H3=d+H3’
e=H4=e+H4’
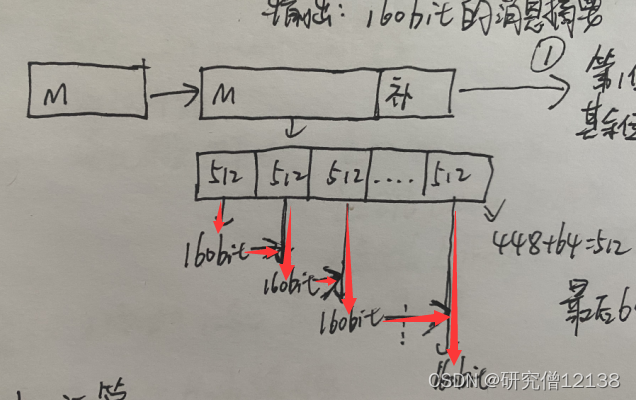
直到最终给出160bit消息摘要
4.2.3 SHA-2
128bit密钥长度的SHA-1已经被Google团队破获,所以SHA-2应运而生,在我的理解…其实就是加长了密钥长度的SHA-1。
(SHA-224、SHA-256、SHA-384、SHA-512)
- SHA-224
输入:0<L<2^64
输出:224bit消息摘要
分组长度:512bit
迭代次数:64次
- SHA-256
输入:0<L<2^64
输出:256bit消息摘要
分组长度:512bit
迭代次数:64次
- SHA-384
输入:0<L<2^256
输出:384bit消息摘要(H0~H5、H6、H7不用)
分组长度:1024bit
迭代次数:80次
- SHA-512
输入:0<L<2^256
输出:512bit消息摘要
分组长度:1024bit
迭代次数:80次

4.2.4 SHA-3
SHA-3较为复杂,SHA-3的详细介绍见我的另外一篇笔记文章。