Misc
签到
知识竞赛题,提交答案抓包,遍历答案即可。
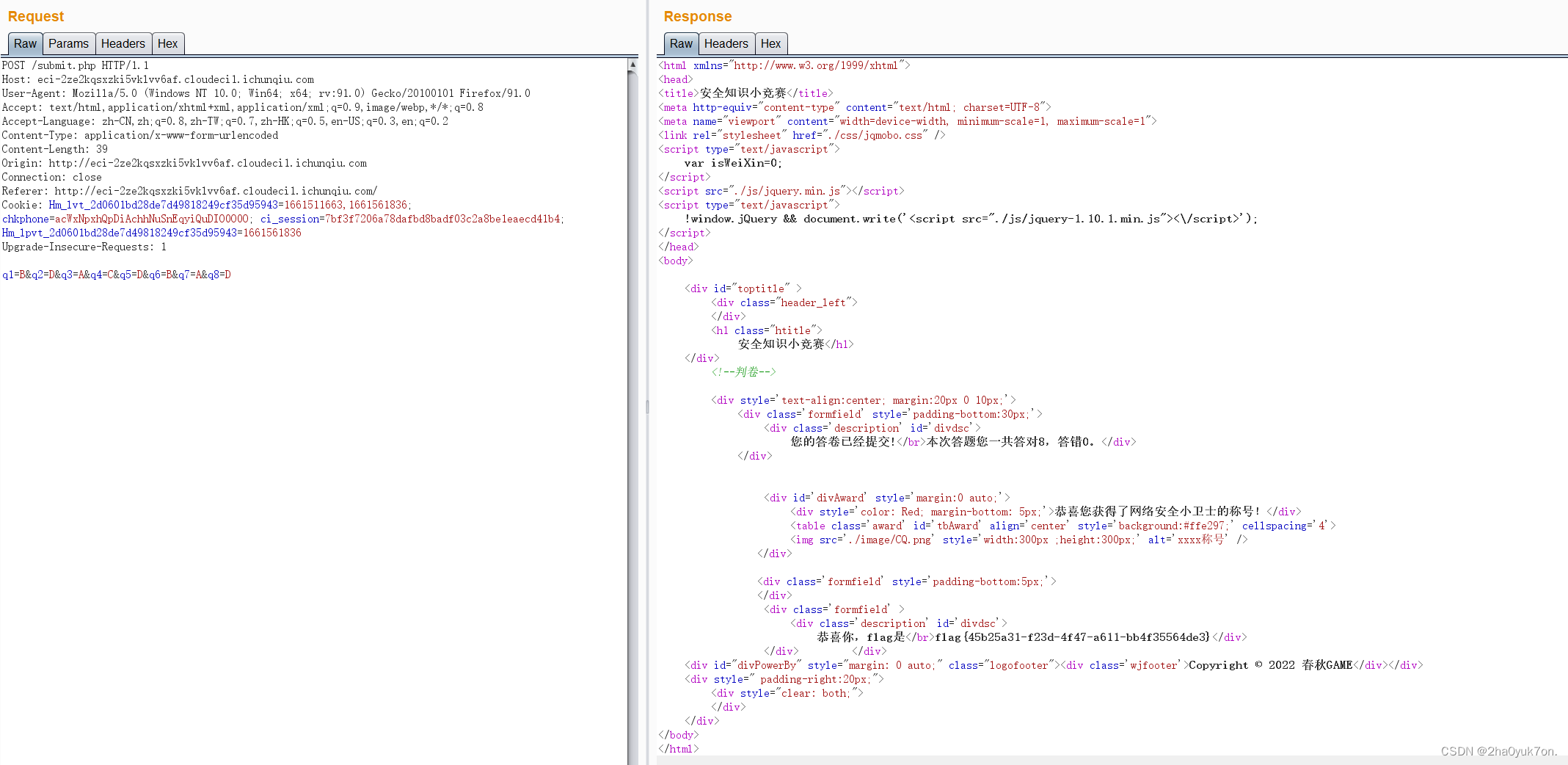
misc620
压缩包密码破解,尝试纯数字暴力破解,得到密码99114514。
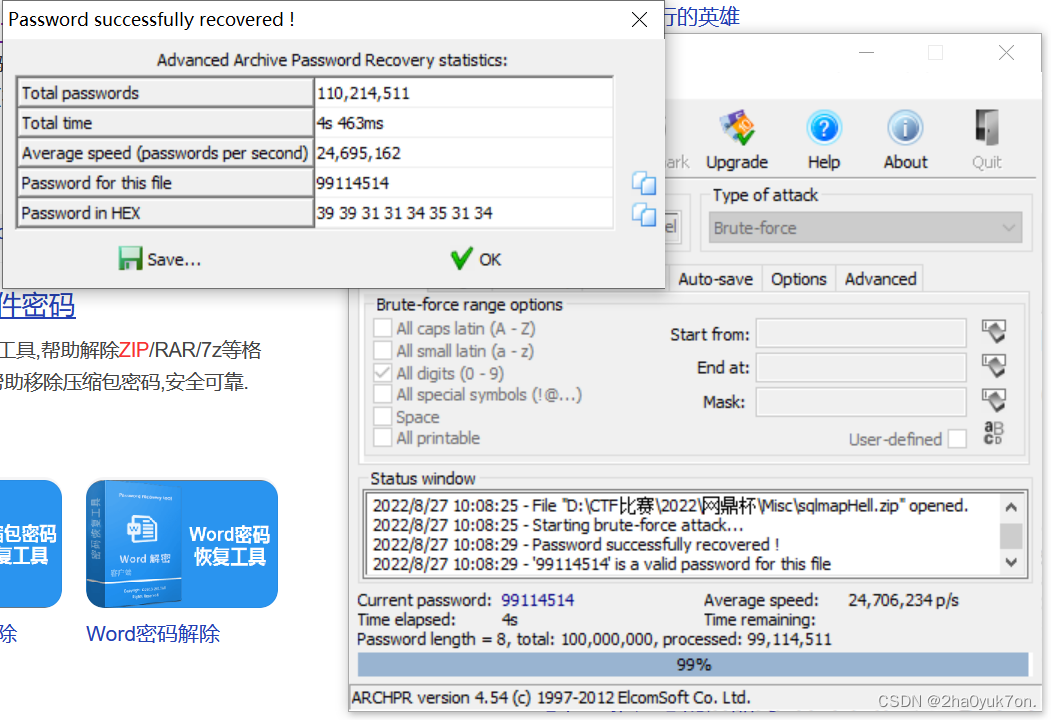
解压得到一个csv表格和另一个加密的7z压缩包,打开表格查看:

在password字段发现疑似Base64编码字符,解码得到压缩包密码。
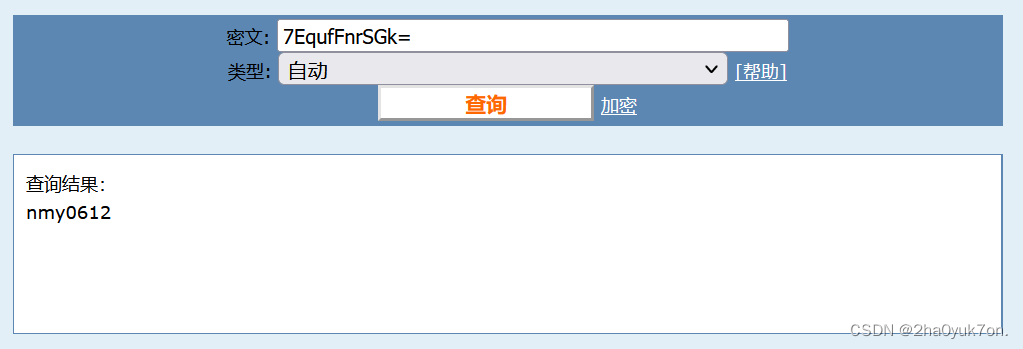
解压压缩包得到如下字符串:
??????????????????????????????????????????????
解对应编码得到flag:
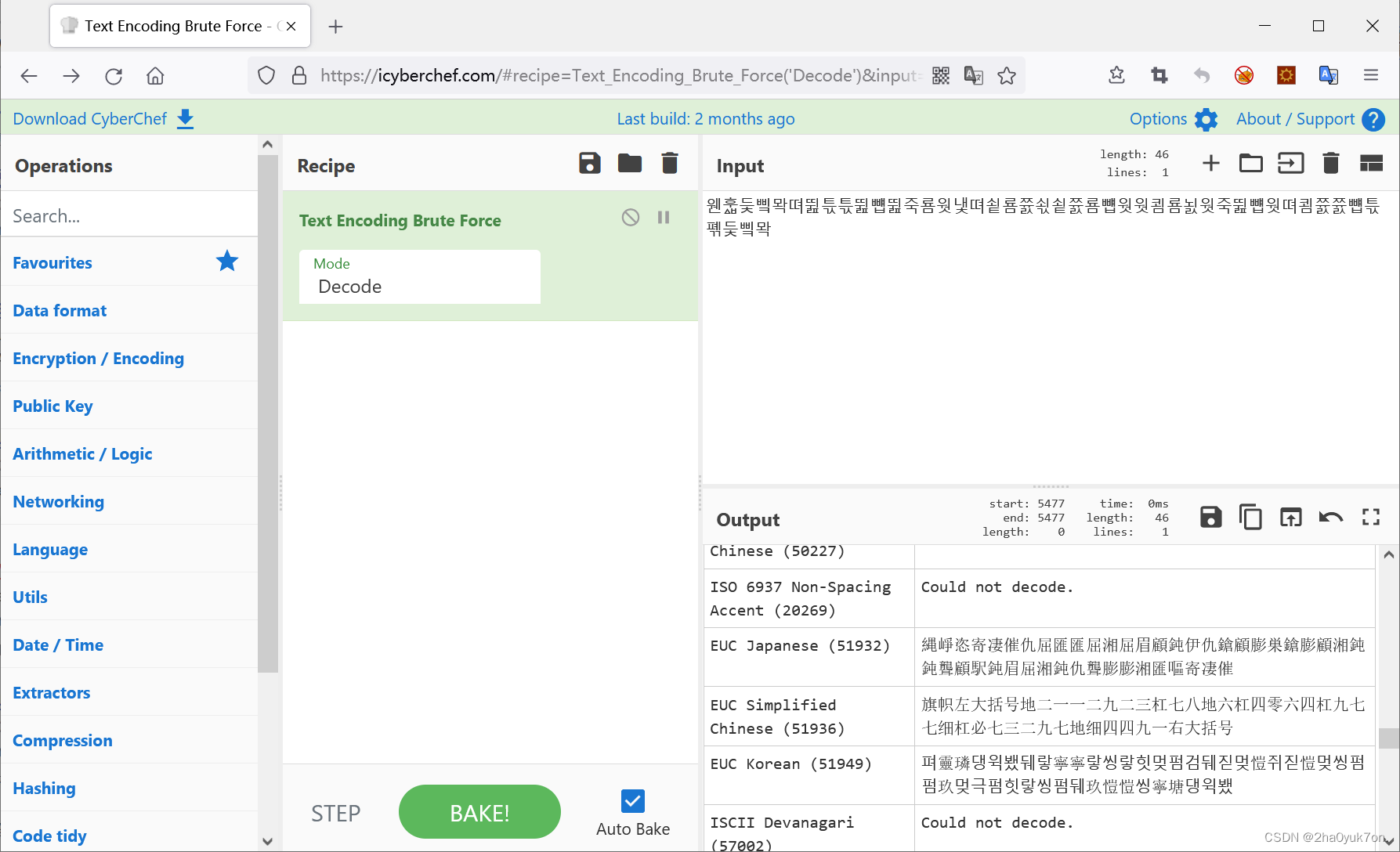
Crypto
crypto582
题目文件:
from Crypto.Util.number import getPrime
import hashlib
e = 2022
m = getPrime(512)
m1 = getPrime(512)
m2 = getPrime(512)
flag = m + m1 + m2
flag = hashlib.md5(str(flag).encode('utf-8')).hexdigest()
c1 = pow(m+m1,e,m*m1)
c2 = pow(m+m2,e,m*m2)
c3 = pow(m1+m2,e,m1*m2)
x = pow(m1+2022,m,m*m1)
y = pow(m2+2022,m,m*m2)
z = pow(m+2022,m1,m*m1)
print('c1 =',c1)
print('c2 =',c2)
print('c3 =',c3)
print('x =',x)
print('y =',y)
print('z =',z)
'''
c1 = 85139434329272123519094184286276070319638471046264384499440682030525456122476228324462769126167628121006213531153927884870307999106015430909361792093581895091445829379547633304737916675926004298753674268141399550405934376072486086468186907326396270307581239055199288888816051281495009808259009684332333344687
c2 = 104554808380721645840032269336579549039995977113982697194651690041676187039363703190743891658905715473980017457465221488358016284891528960913854895940235089108270134689312161783470000803482494370322574472422461483052403826282470850666418693908817591349159407595131136843764544166774390400827241213500917391144
c3 = 94771625845449128812081345291218973301979152577131568497740476123729158619324753128517222692750900524689049078606978317742545997482763600884362992468406577524708622046033409713416026145377740182233674890063333534646927601262333672233695863286637817471270314093720827409474178917969326556939942622112511819330
x = 78237329408351955465927092805995076909826011029371783256454322166600398149132623484679723362562600068961760410039241554232588011577854168402399895992331761353772415982560522912511879304977362225597552446397868843275129027248765252784503841114291392822052506837132093960290237335686354012448414804030938873765
y = 100442166633632319633494450595418167608036668647704883492068692098914206322465717138894302011092841820156560129280901426898815274744523998613724326647935591857728931946261379997352809249780159136988674034759483947949779535134522005905257436546335376141008113285692888482442131971935583298243412131571769294029
z = 104712661985900115750011628727270934552698948001634201257337487373976943443738367683435788889160488319624447315127992641805597631347763038111352925925686965948545739394656951753648392926627442105629724634607023721715249914976189181389720790879720452348480924301370569461741945968322303130995996793764440204452
'''
分析题目文件,可得如下已知条件,其中 c 1 、 c 2 、 c 3 、 x 、 y 、 z c_1、c_2、c_3、x、y、z c1?、c2?、c3?、x、y、z已知:
c
1
≡
(
m
+
m
1
)
e
(
m
o
d
m
?
m
1
)
c_1 \equiv (m+m_1)^e \pmod{m*m_1}
c1?≡(m+m1?)e(modm?m1?)
c
2
≡
(
m
+
m
2
)
e
(
m
o
d
m
?
m
2
)
c_2 \equiv (m+m_2)^e \pmod{m*m_2}
c2?≡(m+m2?)e(modm?m2?)
c
3
≡
(
m
1
+
m
2
)
e
(
m
o
d
m
1
?
m
2
)
c_3 \equiv (m_1+m_2)^e \pmod{m_1*m_2}
c3?≡(m1?+m2?)e(modm1??m2?)
x
≡
(
m
1
+
e
)
m
(
m
o
d
m
?
m
1
)
x \equiv (m_1+e)^m \pmod{m*m_1}
x≡(m1?+e)m(modm?m1?)
y
≡
(
m
2
+
e
)
m
(
m
o
d
m
?
m
2
)
y \equiv (m_2+e)^m \pmod{m*m_2}
y≡(m2?+e)m(modm?m2?)
z
≡
(
m
+
e
)
m
1
(
m
o
d
m
?
m
1
)
z \equiv (m+e)^{m_1} \pmod{m*m_1}
z≡(m+e)m1?(modm?m1?)
由费马小定理可得:
c
1
≡
m
1
e
(
m
o
d
m
)
c_1 \equiv m_1^e \pmod{m}
c1?≡m1e?(modm)
x
≡
(
m
1
+
e
)
(
m
o
d
m
)
x \equiv (m_1+e) \pmod{m}
x≡(m1?+e)(modm)
通过同余式变换构造等量关系:
m
1
e
≡
c
1
(
m
o
d
m
)
m_1^e \equiv c_1 \pmod{m}
m1e?≡c1?(modm)
m
1
e
≡
(
x
?
e
)
e
(
m
o
d
m
)
m_1^e \equiv (x-e)^e \pmod{m}
m1e?≡(x?e)e(modm)
根据同余式的交换性,有:
(
x
?
e
)
e
?
c
1
≡
0
(
m
o
d
m
)
(x-e)^e-c_1\equiv 0 \pmod{m}
(x?e)e?c1?≡0(modm)
同理,也有:
(
y
?
e
)
e
?
c
2
≡
0
(
m
o
d
m
)
(y-e)^e-c_2\equiv 0 \pmod{m}
(y?e)e?c2?≡0(modm)
因此求 ( x ? e ) e ? c 1 (x-e)^e-c_1 (x?e)e?c1?和 ( y ? e ) e ? c 2 (y-e)^e-c_2 (y?e)e?c2?的最大公约数即为 m m m。
根据已知条件,可以得到
m
1
、
m
2
m_1、m_2
m1?、m2?和
m
m
m的关系:
m
1
≡
(
x
?
e
)
(
m
o
d
m
)
m_1 \equiv (x-e) \pmod{m}
m1?≡(x?e)(modm)
m
2
≡
(
y
?
e
)
(
m
o
d
m
)
m_2 \equiv (y-e) \pmod{m}
m2?≡(y?e)(modm)
这里需注意,
m
1
、
m
2
m_1、m_2
m1?、m2?不一定比
m
m
m小,即
m
1
=
x
?
e
+
k
1
m
m_1=x-e+k_1m
m1?=x?e+k1?m
m
2
=
x
?
e
+
k
2
m
m_2=x-e+k_2m
m2?=x?e+k2?m
其中,
k
1
、
k
2
k_1、k_2
k1?、k2?为正整数。经过尝试,发现
k
1
=
0
、
k
2
=
1
k_1=0、k_2=1
k1?=0、k2?=1。
同余:给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。对模m同余是整数的一个等价关系。
EXP:
a1 = (x-e) ** e - c1
a2 = (y-e) ** e - c2
m = sympy.gcd(a1, a2)
m1 = (x - e) % m
m2 = (y - e) % m + m
flag = m + m1 + m2
flag = hashlib.md5(str(flag).encode('utf-8')).hexdigest()
print(flag)
Web
web923
扫描发现存在.git文件泄露。
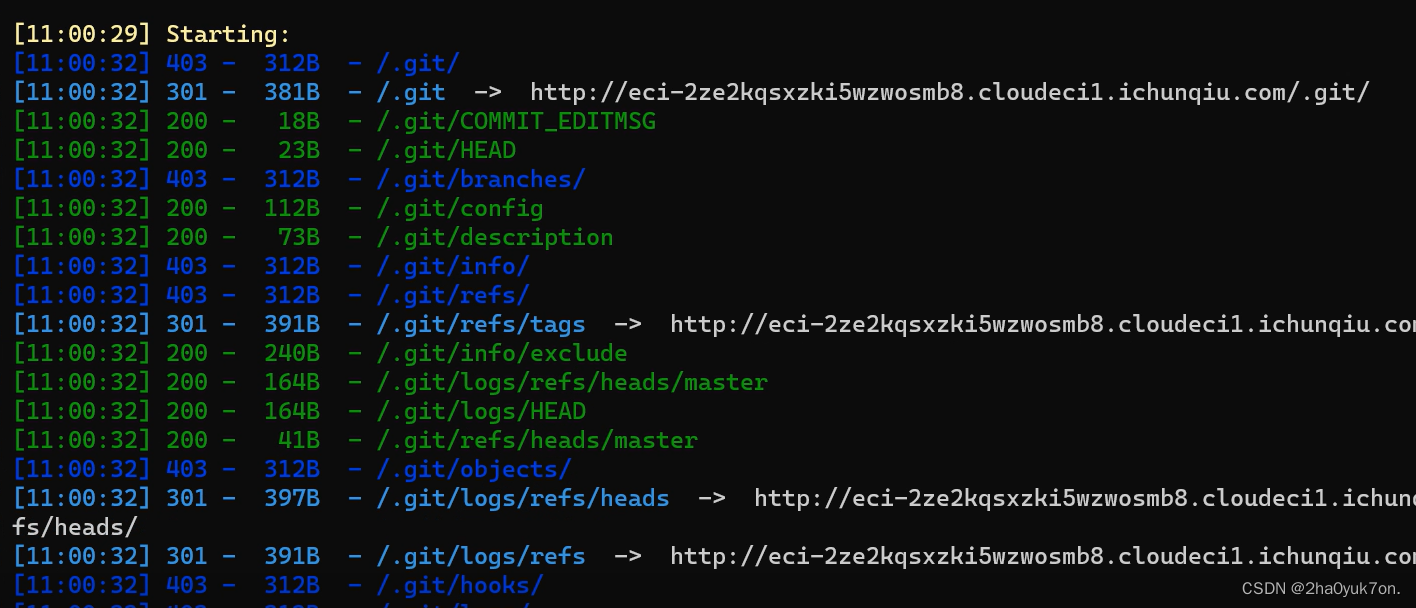
重建还原代码,进行代码审计,发现关键文件application\index\controller\Index.php:
<?php
namespace app\index\controller;
class Index
{
public function index()
{
return '<form method="post" enctype="multipart/form-data" action='.url('index/index/upload').'>
<input type="file" name="hw_file">
<input type="submit" value="上传">';
}
public function upload()
{
if (request()->isPost()){
$file = $_FILES['hw_file']??'';
if(!$file){
return json(['code'=>0,'msg'=>'请选择文件']);
}
$file_name = $file['name'];
$file_tmp = $file['tmp_name'];
$file_size = $file['size'];
if ($file_size > 1024*1024*2){
return json(['code'=>0,'msg'=>'文件大小不能超过2M']);
}
$file_error = $file['error'];
if ($file_error > 0){
return json(['code'=>0,'msg'=>'上传失败']);
}
$file_type = $file['type'];
$file_ext = explode('.',$file_name);
$file_ext = strtolower(end($file_ext));
if(strstr($file_type, "image/")){
if($this->upload_as_image($file_ext, $file_tmp, "../uploads/images/".date('YmdHis')."/", ["gif"], request()->get("hw_file_name")??FALSE)){
return json(['code'=>1,'msg'=>'上传成功']);
} else {
return json(['code'=>0,'msg'=>'上传失败']);
}
} else {
if($this->upload_as_text($file_ext, $file_tmp, "../uploads/files/".date('YmdHis')."/", request()->get("hw_file_name")??FALSE)){
return json(['code'=>1,'msg'=>'上传成功']);
} else {
return json(['code'=>0,'msg'=>'上传失败']);
}
}
} else {
return json(['code'=>0,'msg'=>'请求方式错误']);
}
}
public function upload_as_image($image_type, $image_tmp_file, $upload_base_dir, $file_ext_black_list, $image_filename=FALSE)
{
if(in_array($image_type, $file_ext_black_list)){
return 0;
}
switch ($image_type) {
case 'jpg':
$image_ext = '.jpg';
break;
case 'png':
$image_ext = '.png';
break;
case 'gif':
$image_ext = '.gif';
break;
default:
$image_ext = '.jpg';
break;
}
$image_size = getimagesize($image_tmp_file);
$image_width = $image_size[0];
$image_height = $image_size[1];
if($image_width > 200 || $image_height > 200){
return 0;
}
if ($image_filename === FALSE) {
$image_filename = date('YmdHis') . rand(1000, 9999) . $image_ext;
} else {
$image_filename = $image_filename . $image_ext;
}
if(!file_exists($upload_base_dir)){
mkdir($upload_base_dir, 0777, true);
}
$image_file_path = $upload_base_dir . $image_filename;
rename($image_tmp_file, $image_file_path);
return 1;
}
public function upload_as_text($text_type, $text_tmp_file, $upload_base_dir, $text_filename=FALSE)
{
if(strstr($text_type, "ph") || in_array($text_type, ['php', 'html', 'js', 'css', 'sql', 'phtml', 'shtml', 'php5', 'php7', 'phtm', 'pht', 'php8', 'php4', '.htaccess', 'tpl'])){
return 0;
}
if (strstr($text_filename, ".") || strstr($text_filename, "/")) {
return 0;
}
if( strlen($text_type) == 0){
$text_ext = "";
} else {
if(!ctype_alpha($text_type)){
return 0;
}
$text_ext = "." . $text_type;
}
if ($text_filename === FALSE) {
$text_filename = date('YmdHis') . rand(1000, 9999) . $text_ext;
} else {
$text_filename = $text_filename . $text_ext;
}
if(strlen($text_filename) == 0 || strstr($text_filename, "/") ||!preg_match('/[A-Za-z0-9_]/is', $text_filename)){
return 0;
}
if(!file_exists($upload_base_dir)){
mkdir($upload_base_dir, 0777, true);
}
$text_file_path = $upload_base_dir . "/" . $text_filename;
rename($text_tmp_file, $text_file_path);
return 1;
}
}
是一个文件上传功能,经过代码审计,可以发现有如下逻辑:
- 通过
Content_type字段判断上传文件类型,若是image/类型,则进入上传图像逻辑;否则进入上传文件逻辑; - 上传图像文件扩展名只能是
jpg、png、gif,其他扩展名默认修改为jpg; - 上传文件进行了扩展名的白名单校验,但这里有个逻辑漏洞,校验的是文件名点号后
.的值,因此若文件名为.htaccess时,是可以绕过校验的; - 上传后的文件路径存放在
uploads/images/yyyyMMddHHmmss/下,时间即上传请求的时间,若上送hw_file_name字段,则文件名为该字段值;
综上,利用思路为同时上传.htaccess和木马文件,因为需要确保两个文件在同一目录下,然后连接木马文件即可。
.htaccess上传漏洞原理请见我的另一篇博客:
文件上传漏洞之.htaccess文件解析漏洞-2ha0yuk7on.