[网络协议]Verilog实现DDS IP核

Verilog实现DDS IP核

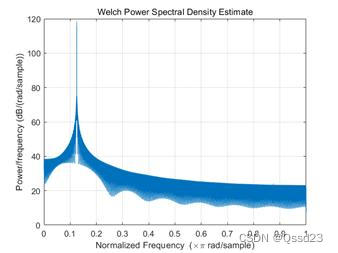
写本文的目的实际上是由于在研究这个问题的时候，发现网上很多dds核的Verilog实现模块都是储存了一个完整的sin波形，但实际上这样就出现了重复信息存储，浪费了存储空间，仅仅只需要1/4个周期即可存储完整的信息，但是如果采用1/4个周期的信号时就很容易出现对称点的错位问题，这样就会使得我们在进行matlab的pwelch验证时，功率谱出现了较大的倍频分量。

一、DDS核简介

首先我们来介绍一下DDS核

DDS信号发生器采用直接数字频率合成(Direct Digital Synthesis，简称DDS)技术，把信号发生器的频率稳定度、准确度提高到与基准频率相同的水平，并且可以在很宽的频率范围内进行精细的频率调节。采用这种方法设计的信号源可工作于调制状态，可对输出电平进行调节，也可输出各种波形。具有频率分辨率高、频率切换时间短、相位连续变化、灵活输出波形、全数字化实现等特点。

二、DDS核原理介绍

DDS核产生正余弦信号实际上是基于奈奎斯特采样定律的。所以我们需要一个高于模拟信号最高频率两倍的抽样频率的离散序列来完成信号的无失真重建过程。所以我们的DDS核需要有一个用于储存抽样的离散序列的
存储空间。

以正弦波为例，假设我们的时钟频率为 $f_c$，共采样n个点，进而我们可到正弦波的频率为

$$f_0=\frac{f_c}{n}$$

我们假设正弦波的一个周期总共采样8个点，那么我们可以得到如下的图像

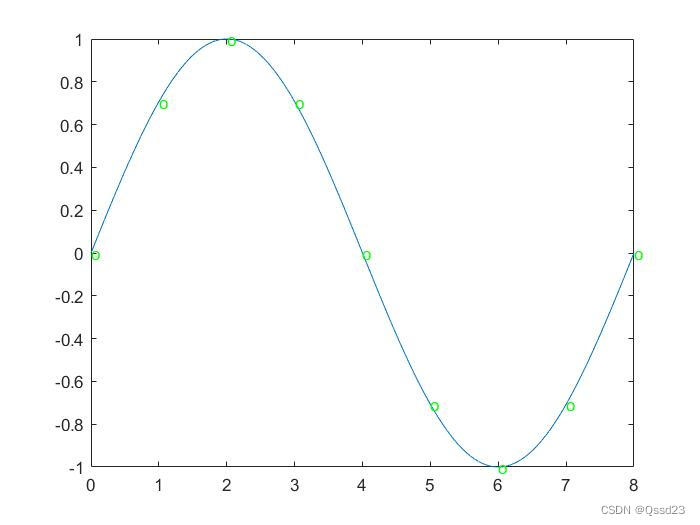
假设我们用于DDS核复原的正弦波一个周期共有$2^N$个采样点。那么我们在复原特定频率的正弦波的时候，我们需要每间隔M个采样点进行一次采样，那么我们一个周期中就包含了存储数据集中的$\frac{2^N}{M}$个数据点，并且准备利用这$\frac{2^N}{M}$个数据点复原一个特定频率的正弦信号，那么则可以得到复原后信号的频率为

$$f_0=\frac{M{f}_c}{2^N}$$

其原理实际上可以理解成一个圆的步进过程，也就是在频率控制字的初值上逐步向上步进累加，得到新的频率控制字，并采用频率控制字作为寻址地址，来获取数据点

综上所述，实际上我们可以得到一个如下的原理流程图

三、DDS核具体代码实现

在这个部分开始之前，我们首先需要明确一下，这里我采用的是48位的频率控制字和4位的幅度控制字进行控制，也就是说输入的频率控制字固定为48位。实际上也可以修改成任意位数，这里选用48位的原因是vivado中的DDS核常采用的硬件控制方式就是48位的频率控制字。同时这里我做了一个没有什么必要的操作，大家可以省略掉这一步。在此处，我把sin信号分成了四路并行输出，然后利用了一个四倍的时钟将这四路信号拼接起来形成最终的完整正弦波形。（大家可以直接利用寻址规则直接得到完整的正弦波形，大可不必像我这么复杂，如果是抱着学习Verilog的态度出发，可以尝试一下我的这个做法）

接下来就是代码部分了，为了防止大家直接照抄，这里只放上部分的代码，如果大家需要完整代码的话，可以试着私信我。

首先，我们使用matlab完成存储的1/4周期coe文件的生成，这里一定要注意的是我们需要在左开右闭的区间内采样1024个点，来得到我们最终的正弦波的数据。

clc;clear;
index = linspace(0,pi/2,depth+1);   
index = index(1:1024);%在左开右闭区间中采样1024个点
sin_value = sin(index);                
sin_value = sin_value * (2^15 -1);  %扩大正弦幅度值    
sin_value = floor((sin_value));
plot(sin_value);
number = [0:depth];
fid=fopen('sin.coe','w+');
fprintf(fid,'memory_initialization_radix=10;\n');
fprintf(fid,'memory_initialization_vector=\n');
for i = 1 : depth - 1  
    fprintf(fid, '%d,\n', sin_value(i));
end
fprintf(fid, '%d;', sin_value(depth));
fclose(fid);

接下来，我们来看Verilog程序的设计部分

首先大家请看我们的端口定义如下

module dds_top(
   input           clk,
   input           clk_fast,   //四倍快的时钟
   input           rst,        //复原信号
   input[47:0]     freq,       //频率控制字
   input[47:0]     phase,      //初始相位控制字
   input[3:0]      width,      //幅度控制字
   output reg [15:0]   sin1,
   output reg [15:0]   sin2,
   output reg [15:0]   sin3,
   output reg [15:0]   sin4,
   output reg [15:0]   cos1,
   output reg [15:0]   cos2,
   output reg [15:0]   cos3,
   output reg [15:0]   cos4,
   output reg [15:0]   sin,
   output reg [15:0]   cos,
   output          valid
   );

接下来，我们根据DDS核的原理图，我们完成对于寻址地址的赋值工作，步进长度即为我们输入的频率控制字，初值即为相位控制字。实际上这里可以设置一个输入的控制信号，来控制输出的是正弦信号还是余弦信号，来减少我们的操作累加的工作。

    always @ (posedge clk or posedge rst) begin
        if(rst) begin
            address_sin1_all <= phase;
            address_sin2_all <= phase + freq;
            address_sin3_all <= phase + freq*2;
            address_sin4_all <= phase + freq*3;
            address_cos1_all <= phase + 48'h3FFF_FFFF_FFFF;
            address_cos2_all <= phase + freq + 48'h3FFF_FFFF_FFFF;
            address_cos3_all <= phase + freq*2 + 48'h3FFF_FFFF_FFFF;
            address_cos4_all <= phase + freq*3 + 48'h3FFF_FFFF_FFFF;
        end
        else begin
            address_sin1_all <= 4*freq + address_sin1_all;
            address_sin2_all <= 4*freq + address_sin2_all;
            address_sin3_all <= 4*freq + address_sin3_all;
            address_sin4_all <= 4*freq + address_sin4_all;
            address_cos1_all <= 4*freq + address_cos1_all;
            address_cos2_all <= 4*freq + address_cos2_all;
            address_cos3_all <= 4*freq + address_cos3_all;
            address_cos4_all <= 4*freq + address_cos4_all;
        end
    end

由于我们存储的数据只有1/4个周期，所以这里我们得到的地址数据并不能直接使用，我们对于位于第二象限和第四象限的角我们就需要进行一个对称的操作，对于位于第三四象限的角我们就需要进行一个正负反转的操作，这样我们才能够得到最终的一个完整版的正弦信号或余弦信号。

对称操作，实际上就是将信号与 48’hFFFF_FFFF_FFFF 进行异或操作，即可得到对应的对称位置的寻址地址，接下来我们再利用修改过的地址进行寻址操作，即可得到我们所需的对应点的值的绝对值。

    always @ (posedge clk or posedge rst) begin
        if(rst) begin
            tmp_sin<= 48'b0;
        end
        else begin
            case(address_sin_all[47:46])
                2'b00:begin
                    tmp_sin <= address_sin_all;
                    flag_sin <= 1'b0;//用于标记正负，0表示为正数，1表示为负数
                end
                2'b01:begin
                    tmp_sin = address_sin_all^48'hFFFFFFFFFFFF;
                    if (tmp_sin[45:36] != 10'b1111_1111_11)begin
                        tmp_sin[45:36] = tmp_sin[45:36] + 10'h1;
                        end
                    flag_sin <= 1'b0;
                end
                2'b10:begin
                    tmp_sin <= address_sin_all;
                    flag_sin <= 1'b1;
                end
                2'b11:begin
                   tmp_sin = address_sin_all^48'hFFFFFFFFFFFF;
                   if (tmp_sin[45:36] != 10'b1111_1111_11)begin
                        tmp_sin[45:36] = tmp_sin[45:36] + 10'h1;
                        end
                   flag_sin <= 1'b1;
                end
                endcase
        end
    end

并利用vivado中的IP核Block Memory Generator完成对于我们生成的coe文件的读取过程。（此处就不赘述IP核调用模块的部分了）

最后我们对寻址完成的绝对值进行处理即可得到最终的结果

always @ (posedge clk or posedge rst) begin
    sin=(flag_sin_over == 1'b0)?(sin_abs/(width)):(-((sin_abs)/(width)));
end

三、仿真结果

这里我们编写一个testbench文件，然后将最终的数据进行分析。

首先我们来看modelsim和vivado联合仿真的结果

在testbench文件中，我们将最终信号写入txt文本中，并将文本的数据导入到matlab中进行pwelch验证，可以得到如下的结果