[网络协议] AES（对称加密）学习记录

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 网络协议 -> AES（对称加密）学习记录 -> 正文阅读

[网络协议]AES（对称加密）学习记录

简单了解

之前学到的RSA加密是非对称加密，而AES则是对称加密，区分点在于AES加密解密过程中用的密钥是相同的。这里记明文为P，密文为C，密钥为K。支持的密钥K的长度有128位，192位，256位。

加密：C = E(P,K)，E为加密函数

解密：P = D(C,K)，D为解密函数

大致加密过程

AES加密过程使用的是分组加密，即把明文P分成n组，对n组明文分别使用密钥K加密得到n组密文，将n组密文组合就得到了最终的密文C。且对每一组明文有长度要求，即128bit位（16个字节，每个字节8位）。可以知道，加密得到的每一组密文的长度也是128bit位。

明文填充

加密过程中，很可能出现明文长度不为128整数倍的情况，这就不能保证每一组的明文长度一致，这时就需要进行填充了。填充的方法有这么几种：NoPadding、PKCS#5、PKCS#7、ISO 10126、ANSI X9.23、ZerosPadding?。可以知道，如果在加密的时候，如果使用了某种填充方法，对应解密也需要用对应的填充方法。

填充方法解释

NoPadding：不填充，只能加密长为128bits倍数的信息，很少使用。

PKCS#5、PKCS#7：缺几个字节，就补充几个字节，且补充的值为缺失字节的数量。举例：{1,2,3,4,5,a,b,c,d,e}，缺少6个字节，则补全为{1,2,3,4,5,a,b,c,d,e,6,6,6,6,6,6}

ISO 10126：最后一个字节是填充的字节数（包括最后一字节），其他全部填随机数

ANSI X9.23：?类似于ISO 10126，只不过ANSI X9.23其他字节填的都是0而不是随机数

ZerosPadding：全部填充0x00，无论缺多少全部填充0x00

详细加密过程

四个步骤：字节替换、行移位、列合和轮密钥加。

注：根据密钥长度不同，加密的轮数也不同，128位的密钥推荐加密轮数为10，192位的密钥推荐加密轮数为12，256位的密钥推荐加密轮数为14。在第一轮之前要进行轮密钥加，即将明文矩阵与密钥矩阵进行异或操作。最后一轮没有进行列混合操作。?

1、字节替换

通过一个替换表（S盒）对每个字节进行替换，且过程是可逆的，将每一个字节的前4位作为行值，后4位作为列值，到t查找，进行输出。
下图为S盒，例如字节为0x16，那么前四位的16进制为1，后四位的16进制为6，去查找S盒中的第1行第6列的值，可以看出为0x47，就把原先的字节0x16替换为0x47。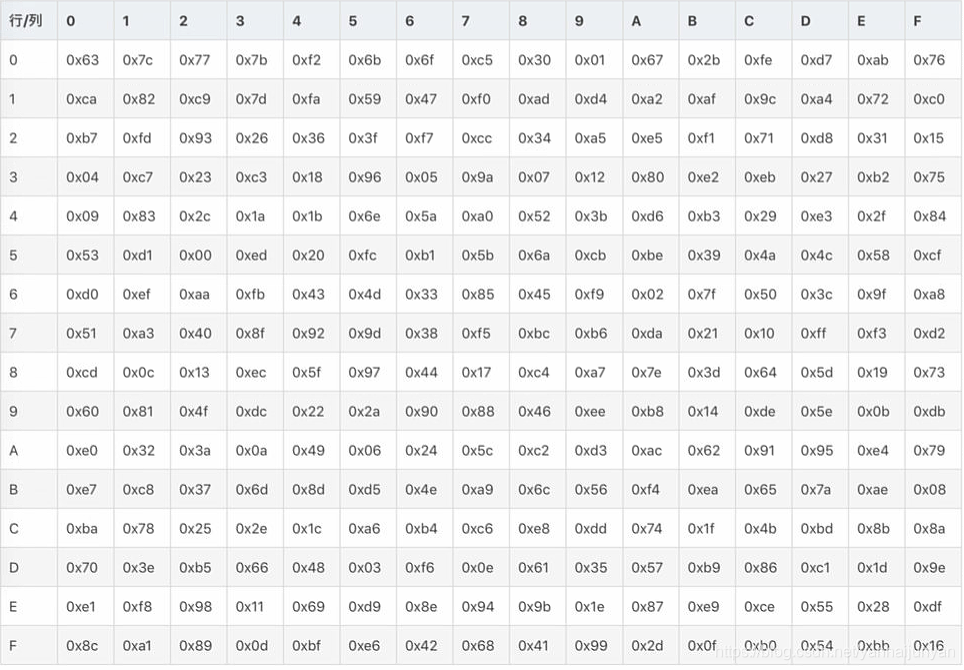
查看源图像

解密过程就是用逆盒进行相同的操作。

2、行移位

将16位的明文P分成16组，放入4*4的矩阵中：

$a_{00}$	$a_{01}$	$a_{02}$	$a_{03}$
$a_{10}$	$a_{11}$	$a_{12}$	$a_{13}$
$a_{20}$	$a_{21}$	$a_{22}$	$a_{23}$
$a_{30}$	$a_{31}$	$a_{32}$	$a_{33}$

顺序位从上到下，从左到右

加密行移位操作：第0行：保持不动；
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?第1行：循环左移1个字节；
? ? ? ? ? ? ? ? ? ? ?????????第2行：循环左移2个字节；
?????????????????????????????第3行：循环左移3个字节。

移位后的明文矩阵：

$a_{00}$	$a_{01}$	$a_{02}$	$a_{03}$
? $a_{11}$	? $a_{12}$	$a_{13}$	? $a_{10}$
? $a_{22}$	? $a_{23}$	$a_{20}$	$a_{21}$
? $a_{33}$	$a_{30}$	? $a_{31}$	? $a_{32}$

解密操作对应进行右移即可。

3、列混合

加密过程：将得到的状态矩阵左乘另一个给定的4*4的矩阵，即给定矩阵*经过行移位的矩阵。

解密过程：只需再次与相乘的矩阵进行异或即可

需要注意的是，这里的矩阵相乘与普通的矩阵相乘不大一样，举例操作：假设给定矩阵第一行为

{02 03 01 01}，经过行移位的矩阵的第一列为{d4 bf 5d 30}，相乘得到：02*d4⊕03*bf⊕5d⊕30，

对02*d4，计算过程为：?

换成二进制形式，(00000010) * (11010100)，d4的二进制最高位为1，此时将d4左移一位再与00011011异或，即(00000010) * (11010100) = (10101000) ⊕ (00011011) = 10110011

若右边的二进制最高位为0，则结果直接为右边的二进制左移一位，即不需再与(00011011)异或。

对03*bf，计算过程为：

换成二进制形式，((00000010)⊕(00000001))*(10111111)，bf的二进制最高位也为1，将bf左移一位再与00011011相异或，

即((00000010)⊕(00000001))*(10111111) = (01111110)?⊕ (00011011) = 11011010

对01*5d，就等于5d，二进制为01011101

对01*30，就等于30，二进制为00110000

最后将每一步的结果进行异或：10110011⊕11011010⊕01011101⊕00110000 =?00000100 = 04