[网络协议] 【网络安全之混淆概念----RSA加解密】

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 网络协议 -> 【网络安全之混淆概念----RSA加解密】 -> 正文阅读

[网络协议]【网络安全之混淆概念----RSA加解密】

背景

上一期我们谈到网络安全常用的对称加密算法AES
本次重点分享我们开发中常见的对称加密----RSA算法

算法RSA简介

非对称加密，顾名思义加解密用的不是同一个密钥，那么非对称加密就得用俩个密钥，一个叫公钥-publicKey，任何人都能够去获取，一个叫私钥-privateKey，不会四处乱传输，保留在一个认定安全的区域，公钥和私钥任意一方加密，只能由另一方解密，自己也是无法解密的，目前全球的数据安全测试中密钥大于1024的密钥还没有人宣称能够破解，因此是安全级别很高的加密算法。

非对称与对称加解密对比

对称加解密
优点：算法公开、计算量小、加密速度快、加密效率高
缺点：秘钥的管理和分发非常困难，不够安全，双方都需要管理好公共秘钥麻烦

非对称加解密
优点：安全性更高，公钥是公开的，秘钥是自己保存的，不需要将私钥给别人
缺点：加密和解密花费时间长、速度慢，只适合对少量数据进行加密。
主要算法：RSA、Elgamal、背包算法、Rabin、HD,ECC（椭圆曲线加密算法）。常见的有：RSA，ECC
综合使用
对称加密算法相比非对称加密算法来说，加解密的效率要高得多。但是缺陷在于对于秘钥的管理上，以及在非安全信道中通讯时，密钥交换的安全性不能保障。所以在实际的网络环境中，会将两者混合使用.。
例如针对C/S模型，
@1、服务端计算出一对秘钥publicKey/privateKey。将私钥保密，将公钥公开。
@2、客户端请求服务端时，拿到服务端的公钥publicKey。
@3、客户端通过AES计算出一个对称加密的秘钥aesKey。然后使用publicKey将aesKey转换成encryptedAesKey。
@4、客户端将加密后的密文发送给服务端。服务端通过privateKey解密获得aesKey。
@5\、然后两边的通讯内容就通过对称密钥X以对称加密算法来加解密。

RSA加解密的原理

基本概念解释

名称	解释
素数	除了1和此整数自身外，不能被其他自然数整除的数
互质	称互素。若N个整数的最大公因子是1，则称这N个整数互质
模运算即求余运算	和模运算紧密相关的一个概念是“同余”。数学上，当两个整数除以同一个正整数，若得相同余数，则二整数同余。比如3/2余1，5/2余1，3、5同余
欧拉函数φ(N)	在RSA中只用两个质数梯减1之积来求欧拉函数值

1、公私钥对产生~秘钥概念
提到密钥，我们不得不提到RSA的三个重要大数：公钥指数e、私钥指数d和模值n。这三个大数是我们使用RSA时需要直接接触
由于RSA密钥是（公钥+模值）、（私钥+模值）分组分发的，单独给对方一个公钥或私钥是没有任何用处，所以我们说的“密钥”其实是它们两者中的其中一组。但我们说的“密钥长度”一般只是指模值的位长度。目前主流可选值：1024、2048、3072、4096…

2、公私钥对产生~公钥指数确定
公钥指数是随意选的，但目前行业上公钥指数普遍选的都是65537（0x10001，5bits），该值是除了1、3、5、17、257之外的最小素数，为什么不选的大一点？当然可以，只是考虑到既要满足相对安全、又想运算的快一点（加密时），PKCS#1的一个建议值而已。有意的把公钥指数选的小一点，但是对应私钥指数肯定很大，意图也很明确，大家都要用公钥加密，所以大家时间很宝贵，需要快一点，您一个人私钥解密，时间长一点就多担待，少数服从多数的典型应用。

3、公私钥对产生~私钥指数确定
公钥指数随意选，那么私钥就不能再随意选了，只能根据算法公式（ed mod k=1，k=(p-1)(q-1)）进行运算出来。那么私钥指数会是多少位？根据ed关系，私钥d=(xk+1)/e（x为任意整数），所以单看这个公式，私钥指数似乎也不是唯一结果，可能大于也可能小于1024bits的，但我们习惯上也是指某个小于1024bits的大整数。包括前文的公钥指数，在实际运算和存储时为方便一般都是按照标准位长进行使用，前面不足部分补0填充，所以，使用保存和转换这些密钥需要注意统一缓冲区的长度。

4、欧拉算法

@1、如果n是质数的某一个次方，即 n = p^k
 (p为质数，k为大于等于1的整数)，则φ(n) = φ( p^k ）-  φ( p^k-1 ）
 也就是φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4
 
@2、如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。
比如5与1、2、3、4都构成互质关系 ，φ(5) = 5-1 = 4、φ(7) = 7-1 = 6。

@3、如果n可以分解成两个互质的整数之积，即 n = p* k ，则φ(n) = φ(p * k) = φ(p1)*φ(p2）
计算56的欧拉函数 φ(56) = φ(8) * φ(7) = 4 * 6 = 24
在我们的RSA加解密中常用的就是 φ(p*k)=(p-1)(k-1)，其中p,另个都是质数。

5、加解密的安全性
用俩个质数 p、q 计算出 n，用n计算出φ(n)，随机选择一个e，计算出d，则公钥私钥产生；而n在公钥私钥中都会出现，因此至关重要，n是p和q相乘得出来，拿到n能否反推出来p和q就是RSA算法是否安全的核心（因为公私钥就三个数值，n、e、d，暴露公钥n、e能否推算d就是安全性高与低的核心），显然1560反推(p-1)(q-1)这俩质数不太难，但是特别大的整数，反推就非常困难，
对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠；只要密钥长度足够长，用RSA加密的信息实际上是不能被解破的。

密钥对生成&加解密

步骤	说明	描述
1	找到两个质数	P、Q
2	计算公共模数	N = P * Q、n的长度就是密钥长度。实际应用中，RSA密钥一般是1024位
3	欧拉函数	φ(N) = (P-1)(Q-1)
4	计算公钥E	1 < E < φ(N)E的取值必须是整数，E 和 φ(N) 必须是互质数
5	计算私钥D	E * D % φ(N) = 1
6	加密	C ＝ M^E mod N C：密文 M：明文
7	解密	M ＝C^D mod N C：密文 M：明文

RSA加密
明文M必须是整数，（字符串可以取ascll码或者Unicode码）且m必须小于n（密钥的长度）而现行的RSA密钥一般是三类：1024位、2048位、4096位,;
首先对明文进行比特串分组，使得每个分组对应的十进制数小于n，然后依次对每个分组m做一次加密，所有分组的密文构成的序列就是原始消息的加密结果，即m满足0<=m<n，则加密算法为：
c≡ m^e mod n， c为密文，且0<=c<n ；对于消息m签名为：sign ≡ m ^d mod n

RSA解密
对于密文0<=c<n，解密算法为：m≡ c^d mod n；
对于消息签名验证：m ≡ sign ^e mod n，则sign是m的有效签名
我们举个栗子：

@1、公钥加密----私钥解密
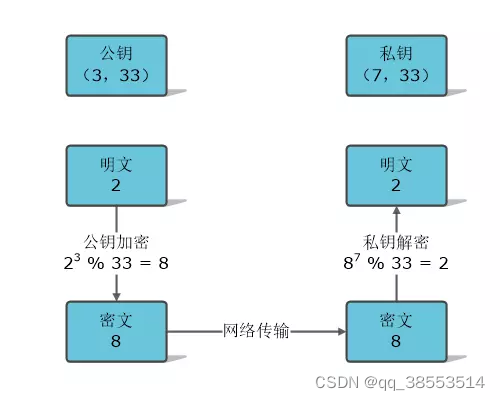
在这里插入图片描述
@1、私钥加签------公钥解签

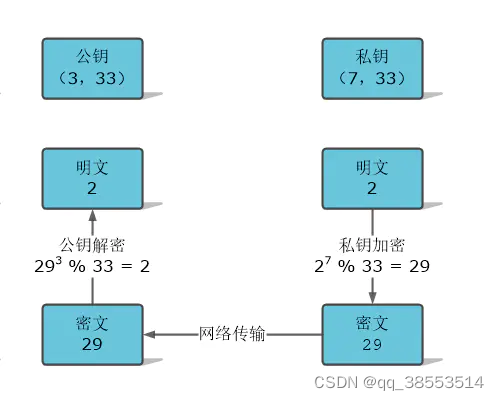
RSA加解密实现

使用原生秘钥key,统一生成加密Key对象

	private static final int KEY_PIR_LENGTH = 1024;

    /**
     * 加密算法
     */
    private static final String RSA_ALGORITHM = "RSA";

    private static final String PRIVATE_KEY_STR = "MIICdQIBADANBgkqhkiG9w0BAQEFAASCAl8wggJbAgEAAoGBAJQkGlPajAsQ+cAtWhaciDo0wRFuMYYynv5DG6XaJ3cCcIVPbnqtcbNw9xnto97HlUoSJELhkd0Ocruy0cd7iqnyWkWD5ghs3yI2WzI12KrzhOgz0iKmbfvS2ioZ2IaW/rdcHUIItmWI91m/azOj5IJzdNoqxQps/05ZowrjpkfVAgMBAAECgYBqF7z/Jro6xqqGljQ5k1sAjH1klU1EdYZmQ/tN+QFges/IuU0+8G5Ie3OMDyPXzYm+JWXwvAkxjkJe6D7SpUh1OrPFcyDgnYt3cLjYFZCy9NjCy2wU+QmbmOWMD3tW/KrcvPRvZ+5U3oYk1nLln+E8VtD685nUoTDPd6EHCJMmlQJBANrb9Vok93p4xbLUain4waS2cOGEc6qqtYKrBG30iu/EiE+8iK2WwQmOBu57FOvU/yIdH7Goc9FEfoGTx6ZtNgcCQQCtR+OHgdoGUvtuRPLOZ8EtXKm6yEBmuZQtQljBukP9IlcxgTEcFWlKn8ccUYz5dujv/0P6xhHz8i5ONYbafLxDAkBtY0r6R0e6WurVOv3lBIQkw1sgHIeDYdde/AM2wec/d8d5sw3NVXAeSnKEd9g5Fzh94Hia30sj6Uwhj69WK3e5AkBx5W/L0PFC+OZlO5KxUwdpzp+NszSJkO+xtAttAwbPavQPCREDmZtEvrL8jSnxi1Re89V2Dx0b0JLZO1uxXw3LAkBF87OJJkIjG2E/+qeA9QZ1TQRR26cv5tEMGjrbls5cz1ewzswtVpJI9fttMLiiXlhV3NaVIjOnUPbvo/Bov3p7";
    private static final String PUBLIC_KEY_STR = "MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQCUJBpT2owLEPnALVoWnIg6NMERbjGGMp7+Qxul2id3AnCFT256rXGzcPcZ7aPex5VKEiRC4ZHdDnK7stHHe4qp8lpFg+YIbN8iNlsyNdiq84ToM9Iipm370toqGdiGlv63XB1CCLZliPdZv2szo+SCc3TaKsUKbP9OWaMK46ZH1QIDAQAB";

    /**
     * 生成公钥和私钥, 秘钥长度1024bit位
     * @throws NoSuchAlgorithmException
     *
     */
    public static Map<String, Object> getKeyPairMap() throws NoSuchAlgorithmException {
        Map<String, Object> keyMap = Maps.newHashMap();

        KeyPairGenerator keyPairGen = KeyPairGenerator.getInstance("RSA");
        keyPairGen.initialize(KEY_PIR_LENGTH);
        KeyPair keyPair = keyPairGen.generateKeyPair();

        keyMap.put("public", keyPair.getPublic());
        keyMap.put("private", keyPair.getPrivate());
        return keyMap;
    }



    /**
     * 根据 publicKey 对象，获取可以传输的 base64 公钥
     * @param publicKey rsa 公钥对象
     * @return 可以传输的 base64 公钥
     */
    public static String getPublicKeyBase64(PublicKey publicKey){
        return Base64.getEncoder().encodeToString(publicKey.getEncoded());
    }


    /**
     * 根据 privateKey 对象，获取可以传输的 base64 私钥
     * @param privateKey rsa 私钥对象
     * @return 可以传输的 base64 私钥
     */
    public static String getPrivateKeyBase64(PrivateKey privateKey){
        return Base64.getEncoder().encodeToString(privateKey.getEncoded());
    }


    /**
     * 根据公钥字符串，创建 RSAPublicKey
     * @param publicKey 公钥字符串
     * @return RSAPublicKey
     * @throws Exception
     */
    public static PublicKey getPublicKey(String publicKey) throws Exception {
        KeyFactory keyFactory = KeyFactory.getInstance(RSA_ALGORITHM);
        byte[] keyBytes = Base64.getDecoder().decode(publicKey);
        X509EncodedKeySpec spec = new X509EncodedKeySpec(keyBytes);
        return keyFactory.generatePublic(spec);
    }

    /**
     * 根据 私钥字符串 创建RSAPrivateKey
     * @param privateKey 私钥字符串
     * @return RSAPrivateKey 对象
     * @throws Exception
     */
    public static PrivateKey getPrivateKey(String privateKey) throws Exception {
        KeyFactory keyFactory = KeyFactory.getInstance(RSA_ALGORITHM);
        byte[] keyBytes = Base64.getDecoder().decode(privateKey);
        PKCS8EncodedKeySpec spec = new PKCS8EncodedKeySpec(keyBytes);
        return keyFactory.generatePrivate(spec);
    }

    /**
     * 使用publicKeyStr 加密数据
     *
     */
    public static String encryptByPublicKeyStr(String message, String publicKeyBase64) throws Exception {
        return StringUtils.isBlank(message)?
            StringUtils.EMPTY : encryptByPublicKey(message, getPublicKey(publicKeyBase64));
    }

    /**
     * 根据私钥串解密
     *
     */
    public static String decryptByPrivateKeyStr(String encryptData, String privateKeyBase64) throws Exception{
        return StringUtils.isBlank(encryptData)?
            StringUtils.EMPTY : decryptByPrivateKey(encryptData, getPrivateKey(privateKeyBase64));
    }

    /**
     * 私钥串加签
     *
     */
    public static String encryptByPrivateKeyStr(String message, String privateKeyBase64) throws Exception {
        return StringUtils.isBlank(message)?
            StringUtils.EMPTY : encryptByPrivateKey(message, getPrivateKey(privateKeyBase64));
    }

    /**
     * 公钥串解签
     *
     */
    public static String decryptByPublicKeyStr(String encryptedData, String publicKeyBase64) throws Exception {
        return StringUtils.isBlank(encryptedData)?
            StringUtils.EMPTY : decryptByPublicKey(encryptedData, getPublicKey(publicKeyBase64));
    }



    /**
     * 使用公钥对象加密
     *
     */
    public static String encryptByPublicKey(String message, PublicKey publicKey) throws Exception {
        if (StringUtils.isBlank(message)){
            return StringUtils.EMPTY;
        }
        Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
        cipher.init(Cipher.ENCRYPT_MODE, publicKey);
        byte[] result = cipher.doFinal(message.getBytes(StandardCharsets.UTF_8));
        return Base64.getEncoder().encodeToString(result);
    }

    /**
     * 使用公钥对象加密
     *
     */
    public static String decryptByPrivateKey(String encryptData, PrivateKey privateKey) throws Exception {
        if (StringUtils.isBlank(encryptData)){
            return StringUtils.EMPTY;
        }
        Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
        cipher.init(Cipher.DECRYPT_MODE, privateKey);
        byte[] result = cipher.doFinal(Base64.getDecoder().decode(encryptData));
        return new String(result, StandardCharsets.UTF_8);
    }

    /**
     * 使用私钥对象加密
     *
     */
    public static String encryptByPrivateKey(String message, PrivateKey privateKey) throws Exception {
        if (StringUtils.isBlank(message)) {
            return StringUtils.EMPTY;
        }
        Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
        cipher.init(Cipher.ENCRYPT_MODE, privateKey);
        byte[] result = cipher.doFinal(message.getBytes(StandardCharsets.UTF_8));
        return Base64.getEncoder().encodeToString(result);
    }

    /**
     * 使用公钥对象解签
     *
     */
    public static String decryptByPublicKey(String encryptedData, PublicKey publicKey) throws Exception {
        if (StringUtils.isBlank(encryptedData)) {
            return StringUtils.EMPTY;
        }
        Cipher cipher = Cipher.getInstance(RSA_ALGORITHM);
        cipher.init(Cipher.DECRYPT_MODE, publicKey);

        byte[] deCodeBytes = cipher.doFinal(Base64.getDecoder().decode(encryptedData));
        return new String(deCodeBytes, StandardCharsets.UTF_8);
    }