? ? ? ? 我们知道Http是一种明文传输的协议,而我们平时也大多接触到的是Http,当然我们也知道它是不安全的因为它传输的报文是明文的,那Https是怎么做到安全的呢?
? ? ? ? 首先来说下Https的链接建立过程:
1.首先客户端发起连接(前提是已经建立TCP链接),发送Client hello。里面内容包括TLS版本号、客户端用于加密的随机数(P)、客户端支持的安全套件信息。
2.服务端收到客户端的请求,发送Server hello。包括服务端生成的用于加密的随机数(G)、选择的客户端的加密套件,也就是TLS_ECDHE_RSA_WITH_AES_256_GCM_SHA384。然后是Server Certificate发送服务端的证书信息。之后是Server key exchange,里面包含生成对称加密的参数,也就是ECDHE算法生成的公钥(Pubkey B),然后服务器用选择的摘要算法(SHA512)将整体信息进行摘要计算,用公钥进行加密,这样做是使用公钥来表示身份防止篡改。然后Server hello done结束。
3.客户端收到请求之后,先根据服务端发送的证书链进行服务端的公钥认证,确认身份。确认身份无误后,根据根据自己本地ECDHE算法生成的Pubkey(A)和服务端的Pubkey(B),生成pre master 。然后根据上两步得到的两个随机数生成master secret。计算的同时发送Client key exchange,也就是客户端的参数(client params),ECDHE算法生成的Pubkey(A)。这里由于是单项认证,客户端无需使用生成摘要表明身份。然后发送Change cipher spec和finished。
4.服务端收到客户端的请求之后,也类似于客户端,根据收到的client params生成pre master,然后再生成master secret。然后发送Change cipher spec和finished。最终完成安全握手连接。之后开始用协商出来的master secret使用对称加密算法加密传输。
? ? ? ? 以上就是基于ECDHE算法人TLS握手过程,可能你并没有看出到底哪里安全了,明明都是明文传输啊?现在来解密一下是怎么安全的(这里只讲和加密算法相关的过程,以简单的DH算法来说明)。
? ? ? ? 首先第一步之后客户端和服务端就共享了一个参数叫做P;第二步完成后两端共享了三个参数P G B;从前两步的描述中我们指定P G都是随机数,可以随便取,取啥都无所谓,那这里的公钥B是怎么回事呢?
? ? ? ? 这就要从DH算法说起了,DH算法的本质是离散对数,什么东西呢?我们中学时学过10^2=100,这里的10叫做底数,2叫做对数,100叫做真数,如果我现在知道底数10和对数2,那么很容易计算出真数100,反过来我现在知道真数100,底数10,你来来算一算对数(当然这里都知道是2),但是这个就不能一下子算出来了,DH算法的关键与此类似(当然并不是简单的对数与指数转换)。举个例子,在DH是这样子来计算的,9^4%25=11,这里9是底数(G),4是对数,25是模数(P),11是真数;反过来说,让你求以9位底数,11为真数,模数为25的对数是多少,这个还能那么容易的计算出来吗?这个就是秘钥交换安全性的关键,这里管计算出来的11叫做公钥,而对数4就是私钥,私钥自己保存,公钥可以公开,有了公钥你也反推不出私钥,如果这个时候再来私钥来作为对称加密算法的秘钥那么不就是实现安全的目标了吗。
? ? ? ? 接着说B是怎么回事?这里先把P G定一下方便接下来的讲解,就假定P=25,G=9吧(还是刚刚的例子)。上面说了P G可以随便取,那么B是怎么来的呢?注意这个可不是随便取的了,而是根据刚刚的DH算法计算出来的,根据DH算法的描述,我们可以把对数作为私钥,所以其实B就是对应到一个私钥的公钥(B可以公开),当然私钥是随便取(也不是那么的随意,必须在1到P-2之间)的,这里就以小b来说明吧,假如b=12,则根据DH算法,B=G^b%P=9^12%25=6,所以B=6。终于说完第二步,如果到这里你理解了B的由来以及P G的意义,那么接下来的第三步就容易了。
? ? ? ? 从前面知道服务器随机选择了小私钥b(12),并根据DH算法计算出了公钥大B(6),同样在第三步中客户端也会随机选择一个私钥a,假定为a=4,则客户端公钥A=G^a%P=9^4%25=11,客户端公钥为A=11,同样这个A是要共享给服务端的,此时两端共享了四个参数P=25 G=9 A=11 B=6,接下来就是关键的就步,生存pre-master,两端都会计算pre-master,就是根基共享的几个参数来计算,客户端pre-master=B^a%P=6^4%25=21,服务端?pre-master=A^b%P=11^12%25=21,看到了吗?此时两端的pre-master是相等的,由于小a说小b并没有在网络上传输(因为他们是私钥啊),而要根据P G A B计算出a b 非常困难,所以a b是安全的,这样的话pre-master也是安全的,由pre-master衍生出来的master secret也就是安全的。后面的会话就可以愉快的使用master secret进行对称加密传输了。
? ? ? ? 这里放个图片理解下为什么最后算出的pre-master是相等的(正是由于DH算法的性质):
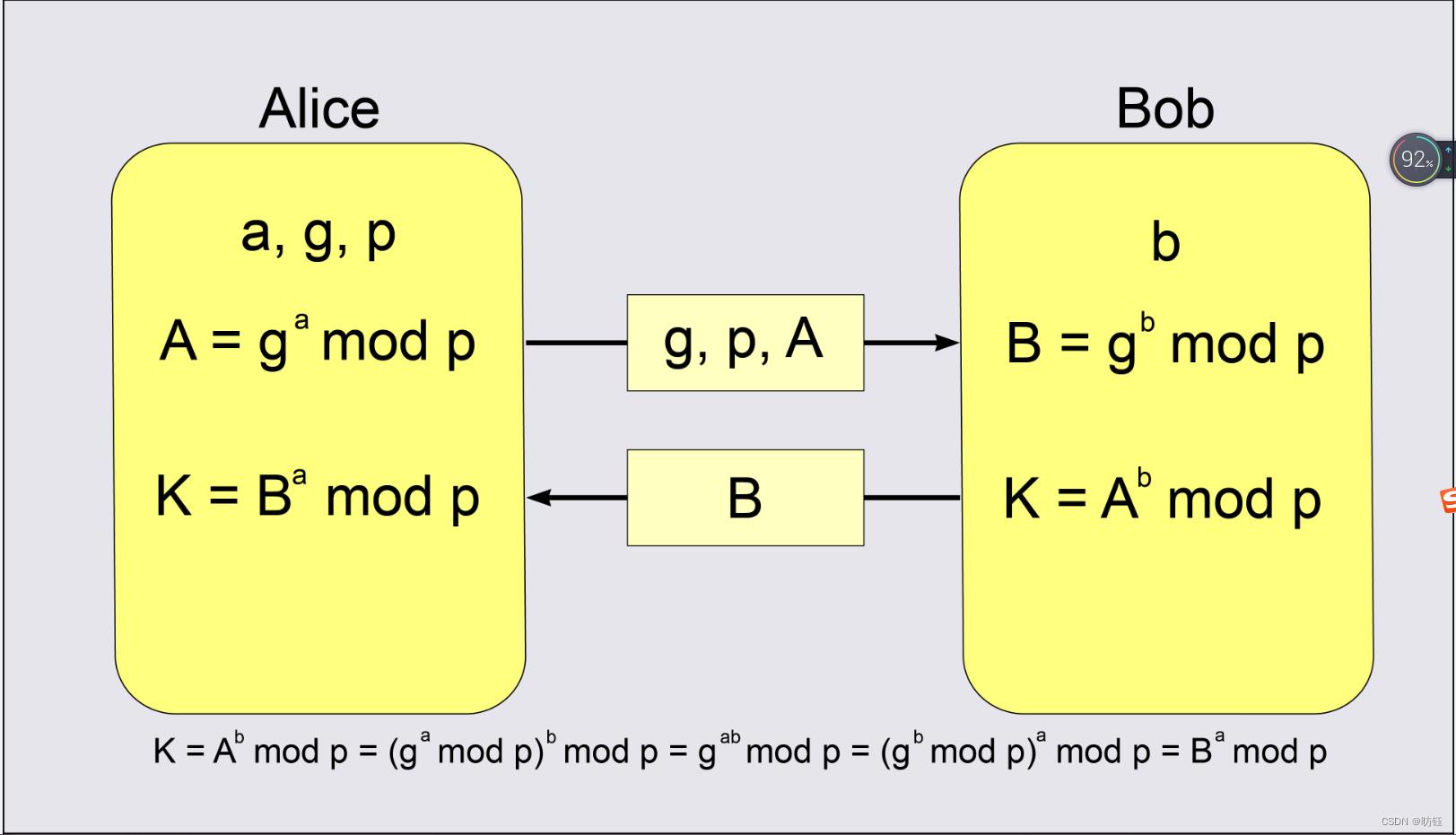
? ? ? ? 注意这里的DH算法只是用来简单说明秘钥交换的过程,便于理解为什么交换秘钥是安全的,实际上真实的TLS环境中使用的秘钥交换算法那才是真正的安全。