摘要:
本课程设计对请求分页存储管理中的六种置换算法进行了模拟,按照我们常见的表示方法进行了输出,并分别求得不同算法及不同页面序列之间的性能曲线图。
整个代码仅使用C语言,这对于只掌握了C语言的同学非常友好。另外需要用到的工具包是EasyX,这是一个比较基础的图形化工具,将用它来完成性能曲线图的绘制(和程序的GUI界面),本博客将一并介绍EasyX工具包的安装方法。
一、课程设计任务描述
请求分页存储管理
(1)请根据理论教材所授内容,采用自己熟悉的编程语言模拟实现OPT、FIFO、LRU、LFU、简单的和改进的CLOCK共六种页面置换算法。
(2)要求:(a) 各置换算法所请求的页面序列是随机产生的,而不是人为输入,在执行时应只需改变页面序列的大小就可以得到不同的页面序列,其中随机性通过一定的参数进行控制而且这些参数要便于调整。(b) 对每一算法,程序依次测试物理块数(内存容量)为2、3、4、5、6、7、8七种情况下的缺页率和置换率,并能自动统计分析出各算法缺页率与物理块、随机性之间的关系(要求程序最终能生成性能曲线图)。(c)? 程序应能动态显示各算法的具体置换过程。
二、需求分析
1、首先,我们需要充分了解六种页面置换算法的具体过程。这部分在教材中已经详细介绍过了,请大家参见《计算机操作系统》教材。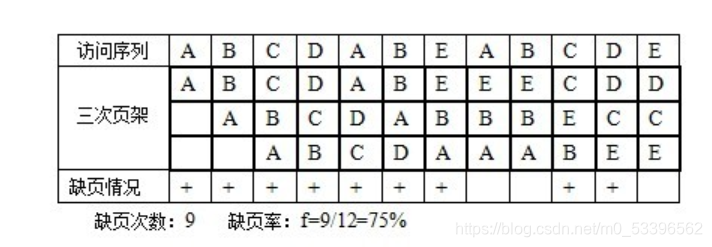
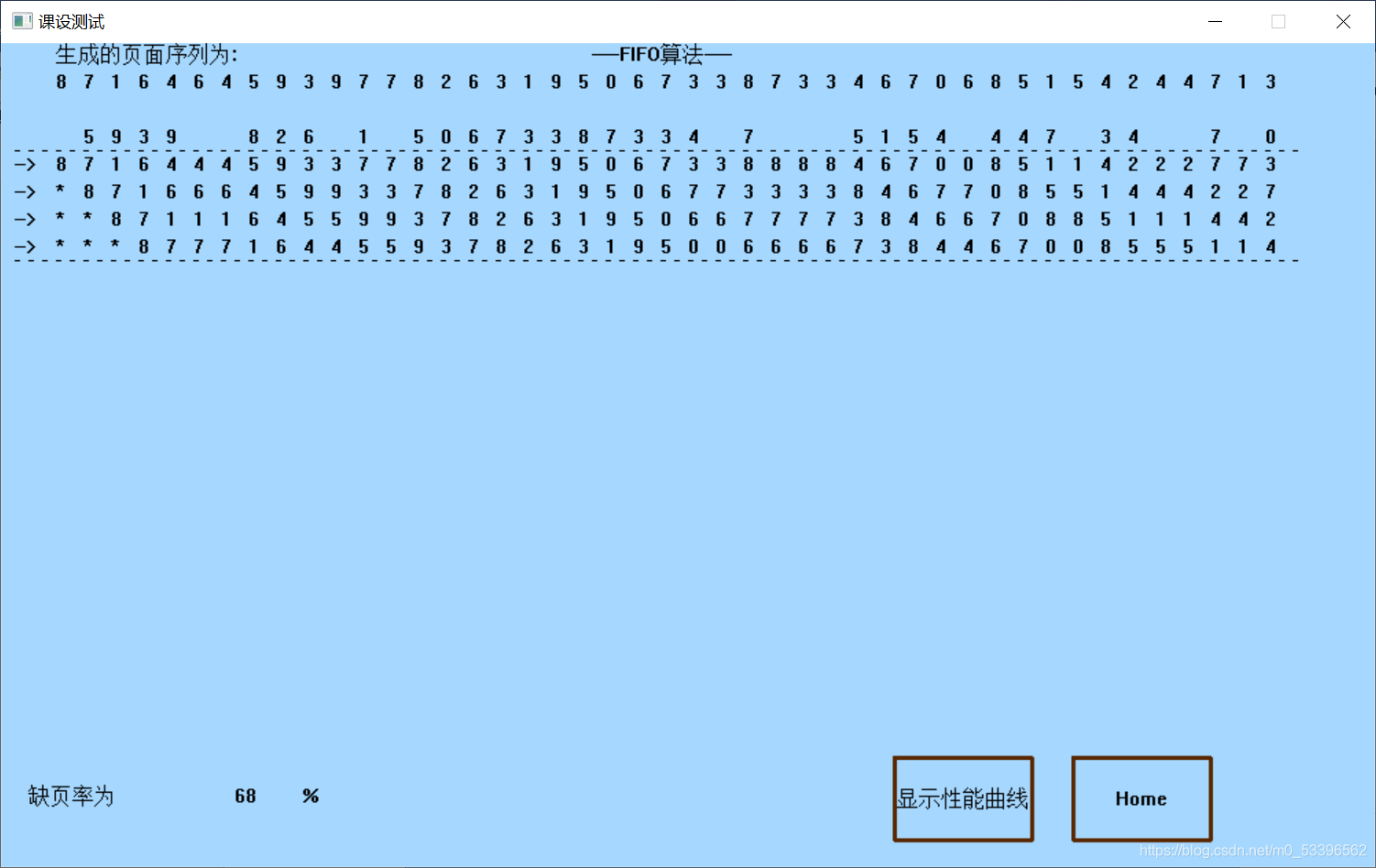
大家对于上图一定非常熟悉,我们将做到输出上图的效果。
我的想法是:为了模拟输出上图,采用一个一维数组numbers[ ]来存放页面序列,一个二维数组stack[ ]来存放每次调用置换算法后,各内存块中的存储情况。
(这里的想法参考了这篇博客)
2、其次,自动生成性能曲线图,无非就是生成一张图表,其横轴为内存块数量,纵轴为缺页率,不同算法用不同颜色的曲线描绘。大致如下图所示:
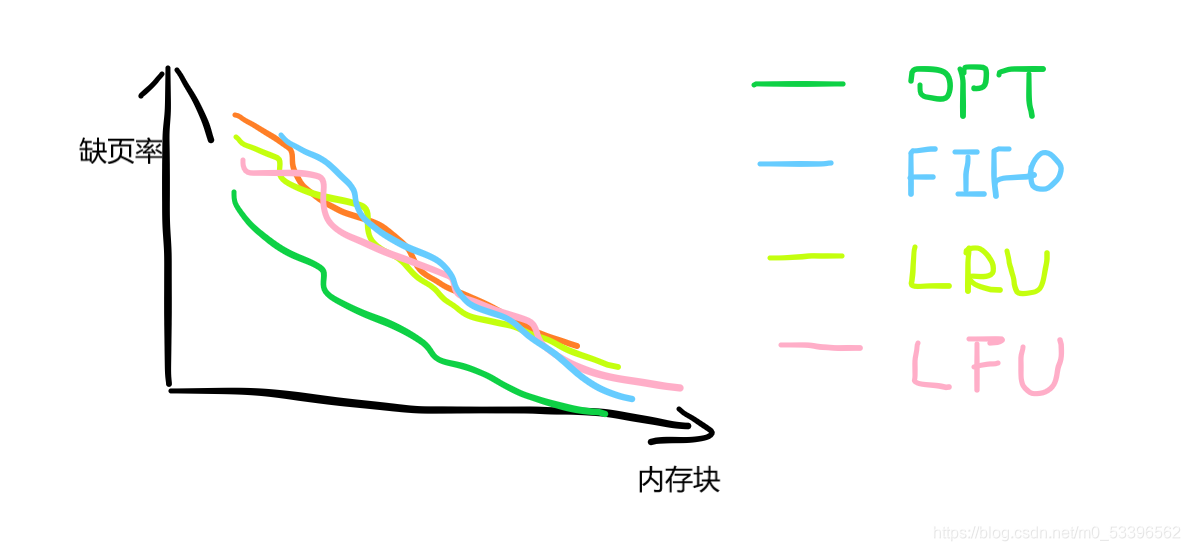
我的想法是,利用EasyX库实现作图(然而后来直接一口气做出了图形化操作界面hhh)
下面介绍EasyX的安装:
第一步:下载EasyX包????????https://easyx.cn/
第二步:打开,点下一步,选择你想安装到的开发平台(请同时安装文档,这非常有用!)
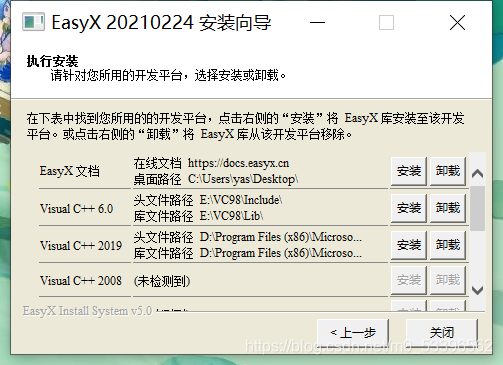
第三步:安装完成
在使用时,引用头文件即可
#include <graphics.h> // 引用图形库头文件
#include <conio.h>?三、实现过程
1、每个置换算法写成一个函数。
2、一些数据结构(如页面序列numbers[ ],页面栈stack[ ]等)设置为全局变量。
3、一些变量(如序列长度l,内存块个数nums等)设计成由用户输入。
4、各置换算法原理这里不叙述,请大家翻书或查找专门资料或直接读代码hhh
完成上述几条后,基本的框架也就出来了,下面展示该“框架”的代码:(缩进很奇怪请忽略)
//框架
//@Dwyanelittle64c
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <windows.h>
#define MAXSIZE 100
int numbers[MAXSIZE]; //存放页面序列的数组
int nums=0; //内存块的个数
int l=0; //序列个数
int stack[8][MAXSIZE]; //页面栈数组
void begin();
void randomnum(); //用于产生随机数
void init(); //初始化
void FIFO(); //FIFO算法
void LRU(); //LRU算法
void OPT(); //最优页面置换算法(OPT)
void LFU(); //LFU算法
void SClock(); //
void IClock(); //
void print(); //输出页面栈
int MAX(int w[]); //返回max元素下标
int MIN(int w[]); //返回min元素下标
int main()
{
begin();
FIFO();
LRU();
OPT();
LFU();
SClock();
IClock();
return 0;
}
void begin()//开始菜单界面
{
int i;
printf("请输入页面序列的数量(1-100):");
scanf("%d",&l);
printf("请输入内存块的数量(2-8):");
scanf("%d",&nums);
randomnum();//生成随机页面
printf("页面引用串为:\n");
for(i=0;i<l;i++)
printf("%d ",numbers[i]);
printf("\n");
}
void randomnum()//如果需要使用随机数生成输入串,调用该函数
{
int i;
srand(time(0));//设置时间种子
for(i = 0; i < l; i++)
numbers[i] = rand() % 10;//生成区间0`9的随机页面引用串
}
void init() //用于每次初始化页面栈中内容
{
int i,j;
for(i=0;i<nums;i++)
for(j=0;j<l;j++)
stack[i][j]=-1;
}
void print() //输出各个算法的栈的内容
{
int i,j;
for(i=0;i<nums;i++)
{
for(j=0;j<l;j++)
{
// Sleep(500);
if(stack[i][j]==-1)
printf("* ");
else
printf("%d ",stack[i][j]);
}
printf("\n");
}
}
int MAX(int w[])
{
int i;
int max_val=w[0],max_loc=0;
for(i=0;i<nums;i++)
{
if(w[i]>max_val)
{
max_loc=i;
max_val=w[i];
}
}
// printf("max_val=%d,max_loc=%d\n",max_val,max_loc);
return max_loc;
}
int MIN(int w[])
{
int i;
int min_val=w[0],min_loc=0;
for(i=0;i<nums;i++)
{
if(w[i]<min_val)
{
min_loc=i;
min_val=w[i];
}
}
return min_loc;
}
void FIFO()
{
int i,j,n=0,flag;
init();
stack[0][0]=numbers[0];
for(j=1;j<l;j++)
{
flag=0;
for(i=0;i<nums;i++) //将上一列复制过来
stack[i][j]=stack[i][j-1];
for(i=0;i<nums;i++)
{
if (stack[i][j]==numbers[j])
{
flag=1; //找到匹配,置标志位为1
break;
}
}
if(flag==0) //未找到匹配
{
for(i=nums-2;i>=0;i--)
stack[i+1][j]=stack[i][j]; //将最远的元素弹出
stack[0][j]=numbers[j]; //新元素进入
n++; //计数器+1
}
}
printf("\n");
printf("FIFO算法:\n");
print();
printf("缺页错误数目为:%d\n",n);
printf("缺页率为:%.2f\n",float(n)/l);
}
void LRU()
{
int i,j,n=0,flag,i_loc,i_val;
init();
stack[0][0]=numbers[0];
for(j=1;j<l;j++)
{
flag=0;
for(i=0;i<nums;i++) //将上一列复制过来
stack[i][j]=stack[i][j-1];
for(i=0;i<nums;i++)
{
if (stack[i][j]==numbers[j])
{
flag=1; //命中,置标志位为1
i_loc=i; //记录i的位置
i_val=stack[i][j]; //记录i的值
break;
}
}
if(flag==0) //未命中
{
for(i=nums-2;i>=0;i--)
stack[i+1][j]=stack[i][j]; //将最远的元素弹出
stack[0][j]=numbers[j]; //新元素进入
n++; //计数器+1
}
if(flag==1) //命中
{
for(i=i_loc-1;i>=0;i--) //令命中元素置顶
{
stack[i+1][j]=stack[i][j]; //error
}
stack[0][j]=i_val;
}
}
printf("\n");
printf("LRU算法:\n");
print();
printf("缺页错误数目为:%d\n",n);
printf("缺页率为:%.2f\n",float(n)/l);
}
void OPT()
{
int i,j,k,n=0; //k表示寻找w数组时的j
int flag=0,i_loc,flag_0,flag_i; //flag表示是否命中,flag_0表示是否有空内存块,flag_i表示空内存块位置
int w[8]; //权重数组
for(i=0;i<8;i++)
w[i]=MAXSIZE;
init();
stack[0][0]=numbers[0];
for(j=1;j<l;j++)
{
flag=0;
for(i=0;i<nums;i++)
stack[i][j]=stack[i][j-1];
for(i=0;i<nums;i++)
if (stack[i][j]==numbers[j]) //判断是否命中
{
flag=1;
break;
}
flag_0=0; //flag_0置零
for(i=0;i<nums;i++)
if(stack[i][j]==-1) //判断是否有空块
{
flag_0=1;
flag_i=i;
break;
}
if(flag!=1) //未命中
{
if(flag_0==1) //有空页
stack[flag_i][j]=numbers[j];
else
{
for(i=0;i<nums;i++)
{
for(k=j;k<l;k++)
{
if(stack[i][j]==numbers[k])
{
w[i]=k;
break;
}
}
}
i_loc=MAX(w); //max函数返回数组w中最大元素的下标
stack[i_loc][j]=numbers[j];
}
n++; //计数器++
}
}
printf("\n");
printf("OPT算法:\n");
print();
printf("缺页错误数目为:%d\n",n);
printf("缺页率为:%.2f\n",float(n)/l);
}
void LFU()
{
int i,j,n=0; //k表示寻找w数组时的j
int flag=0,i_loc,flag_0,flag_i; //flag表示是否命中,flag_0表示是否有空内存块,flag_i表示空内存块位置
int w[8]={0}; //访问计数器
init();
stack[0][0]=numbers[0];
for(j=1;j<l;j++)
{
flag=0;
for(i=0;i<nums;i++)
stack[i][j]=stack[i][j-1];
for(i=0;i<nums;i++)
if (stack[i][j]==numbers[j])//判断是否命中
{
flag=1;
w[i]++;
break;
}
flag_0=0; //flag_0置零
for(i=0;i<nums;i++)
if(stack[i][j]==-1) //判断是否有空块
{
flag_0=1;
flag_i=i;
break;
}
if(flag!=1) //未命中
{
if(flag_0==1) //有空页
stack[flag_i][j]=numbers[j];
else
{
i_loc=MIN(w); //max函数返回数组w中最大元素的下标
stack[i_loc][j]=numbers[j];
w[i_loc]=0;
}
n++; //计数器++
}
}
printf("\n");
printf("LFU算法:\n");
print();
printf("缺页错误数目为:%d\n",n);
printf("缺页率为:%.2f\n",float(n)/l);
}
void SClock()
{
int i,j,n=0; //k表示寻找w数组时的j
int flag=0,flag_0,flag_i; //flag表示是否命中,flag_0表示是否有空内存块,flag_i表示空内存块位置
int a[8]={0}; //访问位数组
int ii=0; //代替指针
init();
stack[0][0]=numbers[0];
for(j=1;j<l;j++)
{
flag=0;
for(i=0;i<nums;i++) //将上一列的复制过来
stack[i][j]=stack[i][j-1];
for(i=0;i<nums;i++)
{
if (stack[i][j]==numbers[j])//判断是否命中
{
flag=1;
a[i]=1;
ii=(ii+1)%nums;
break;
}
else
{
a[i]=0;
ii=(ii+1)%nums;
}
}
flag_0=0; //flag_0置零
for(i=0;i<nums;i++)
if(stack[i][j]==-1) //判断是否有空块
{
flag_0=1;
flag_i=i;
break;
}
if(flag!=1) //未命中
{
if(flag_0==1) //有空页
{
stack[flag_i][j]=numbers[j];//插入数据
a[flag_i]=1; //访问位 置1
ii=(ii+1)%nums; //循环+1
}
else
{
stack[ii][j]=numbers[j];
a[i]=1;
ii=(ii+1)%nums;
}
n++; //计数器++
}
}
printf("\n");
printf("SClock算法:\n");
print();
printf("缺页错误数目为:%d\n",n);
printf("缺页率为:%.2f\n",float(n)/l);
}
void IClock()
{
int i,j,n=0;
int flag=0,flag_0,flag_i; //flag表示是否命中,flag_0表示是否有空内存块,flag_i表示空内存块位置
int t1=0,t2=0,t3=0; //扫描轮次
int a[8]={0}; //访问位数组
int m[8]={0}; //修改位数组
int ii=0; //代替指针
init();
stack[0][0]=numbers[0];
for(j=1;j<l;j++)
{
flag=0;
for(i=0;i<nums;i++) //将上一列的复制过来
stack[i][j]=stack[i][j-1];
for(i=0;i<nums;i++)
{
if (stack[i][j]==numbers[j])//判断是否命中
{
flag=1;
a[i]=1;
ii=(ii+1)%nums;
break;
}
else
{
a[i]=0;
ii=(ii+1)%nums;
}
}
flag_0=0; //flag_0置零
for(i=0;i<nums;i++)
if(stack[i][j]==-1) //判断是否有空块
{
flag_0=1;
flag_i=i;
break;
}
if(flag!=1) //未命中
{
if(flag_0==1) //有空页
{
stack[flag_i][j]=numbers[j];//插入数据
a[flag_i]=1; //访问位 置1
ii=(ii+1)%nums; //循环+1
}
else //未命中(教材p167)
{
for(i=0;i<nums;i++) //第一次扫描
if(a[i]==0 && m[i]==0)
{
stack[i][j]=numbers[j];
t1=1;
break;
}
if(t1==0)
for(i=0;i<nums;i++) //第二次扫描
{
a[i]=1; //A置1
if(a[i]==0 && m[i]==1)
{
stack[i][j]=numbers[j];
t2=1;
break;
}
}
if(t2==0) //第三次扫描
{
for(i=0;i<nums;i++)
a[i]=0; //整体A置0
for(i=0;i<nums;i++)
if(a[i]==0 && m[i]==0)
{
stack[i][j]=numbers[j];
t3=1;
break;
}
}
if(t3==0) //第三次后半截扫描
{
for(i=0;i<nums;i++)
{
if(a[i]==0 && m[i]==1)
{
stack[i][j]=numbers[j];
t2=1;
break;
}
}
}
}
n++; //计数器++
}
}
printf("\n");
printf("IClock算法:\n");
print();
printf("缺页错误数目为:%d\n",n);
printf("缺页率为:%.2f\n",float(n)/l);
}?运行结果如图:
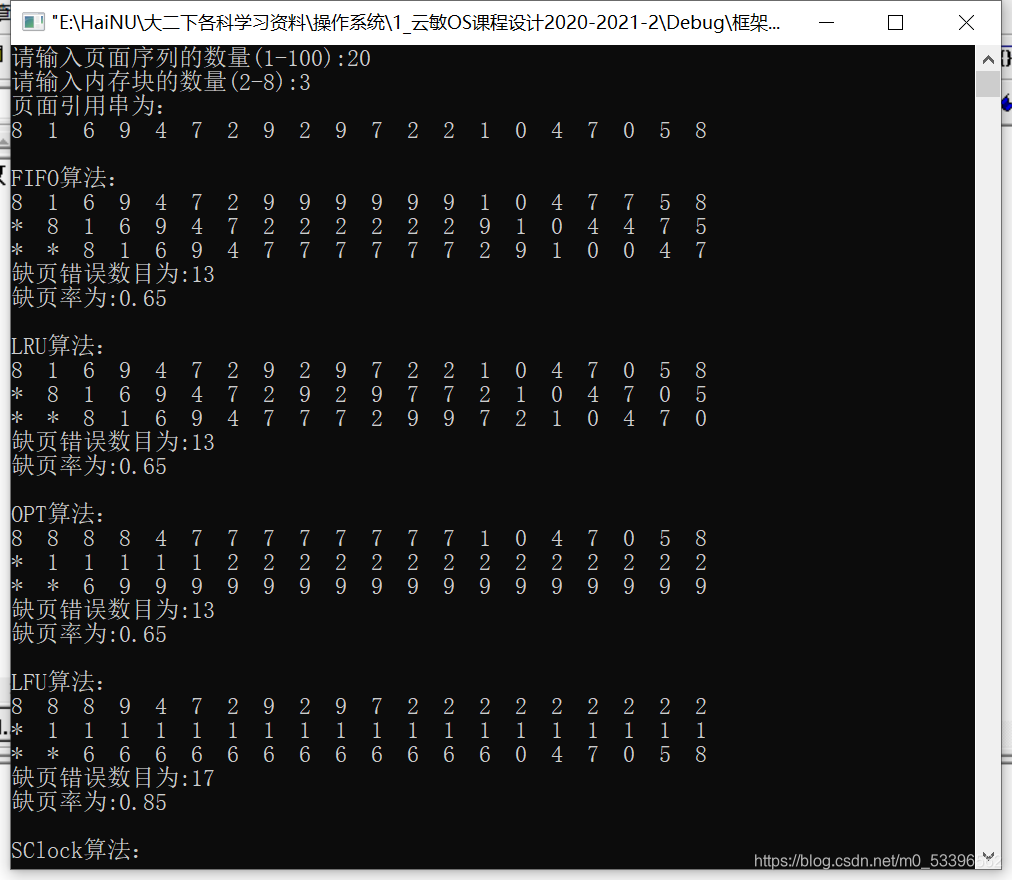
做到这儿,课程设计及格应该是没问题了。但我们还有两个任务没有完成:
实现 随机性的控制? 和? 自动生成性能曲线图
1、首先做简单一点的前者,我的理解是,假设随机性用参数x控制。x越小,则生成的页面序列前后之间相关性越小,即越随机;x越大,则生成的页面序列前后之间相关性越大,即越不随机。这样理解后,代码实现就很简单了,只需稍作修改:
void randomnum(int x)//如果需要使用随机数生成输入串,调用该函数,x表示随机性参数
{
int i, k, n;
srand(time(0));//设置时间种子
for (i = 0; i < l; i++)
{
numbers[i] = rand() % 10; //生成区间0`9的随机页面引用串
if (i > 0 && numbers[i] != numbers[i - 1])
{
for (k = 0;k < x;k++) //控制随机值的随机性
{
numbers[i] = rand()%10;
if (numbers[i] == numbers[i - 1])
break;
}
}
}
}2、然后是生成性能曲线图。关于该图表的描述前面已经介绍过了。
我的想法是:先将原始数据存放起来(如使用二维数组存放:某个页面序列下,不同算法之间的缺页率; 或是在某个算法中,不同内存块数之间的缺页率等),然后利用easyx包中提供的函数,将对应的数据画成图的形式即可。
(本人参考这篇博客入门easyx的)
比如说:用啥啥啥函数创建一个窗口,用line()函数绘制一条线段,用outtextxy()函数在指定位置输出字符串噔噔蹬蹬。
??????????????????????????????????????? ??? 详情请参见easyx文档说明!(请一定去看!)

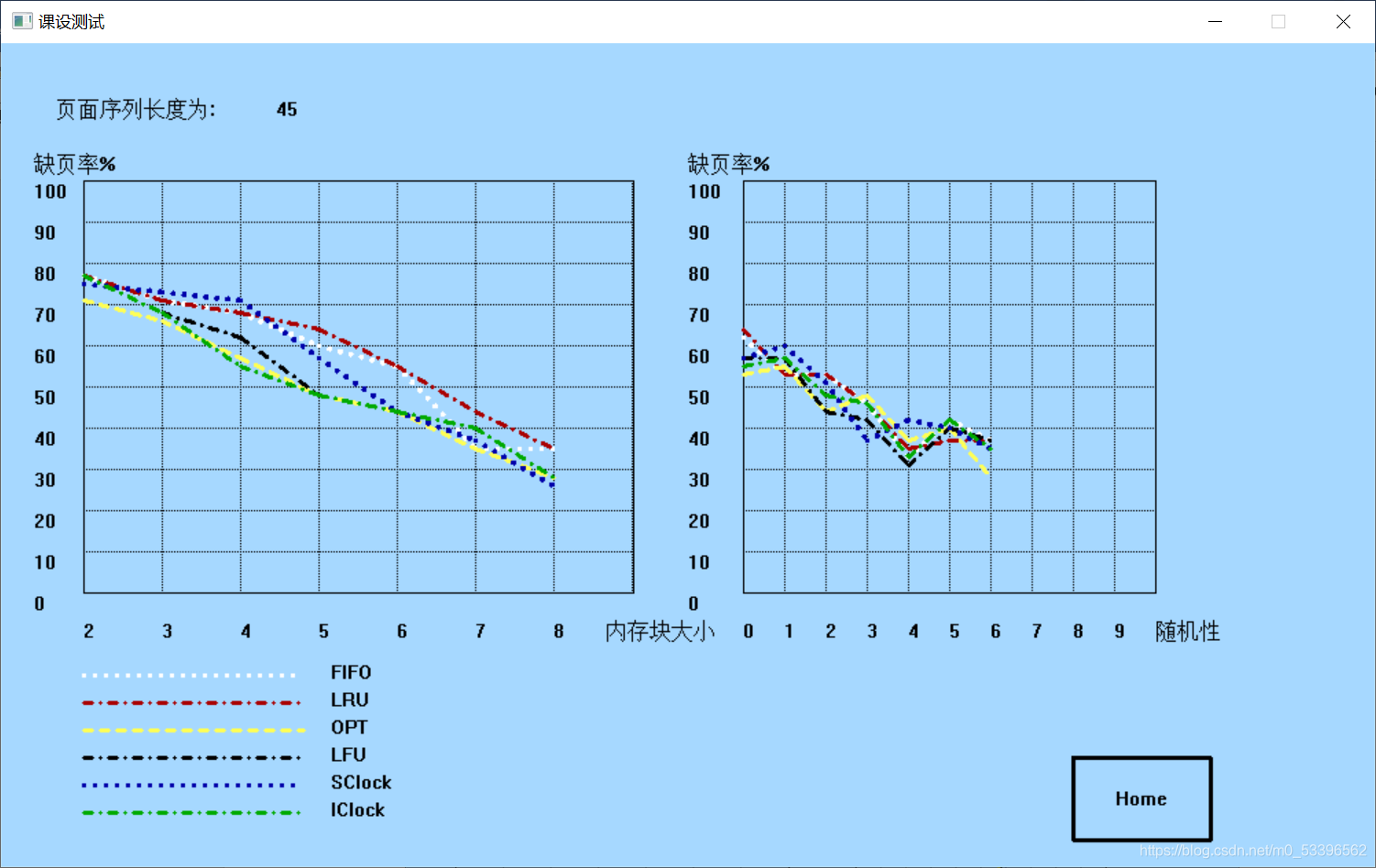
?本人做出来的 性能曲线图 大概长这样:
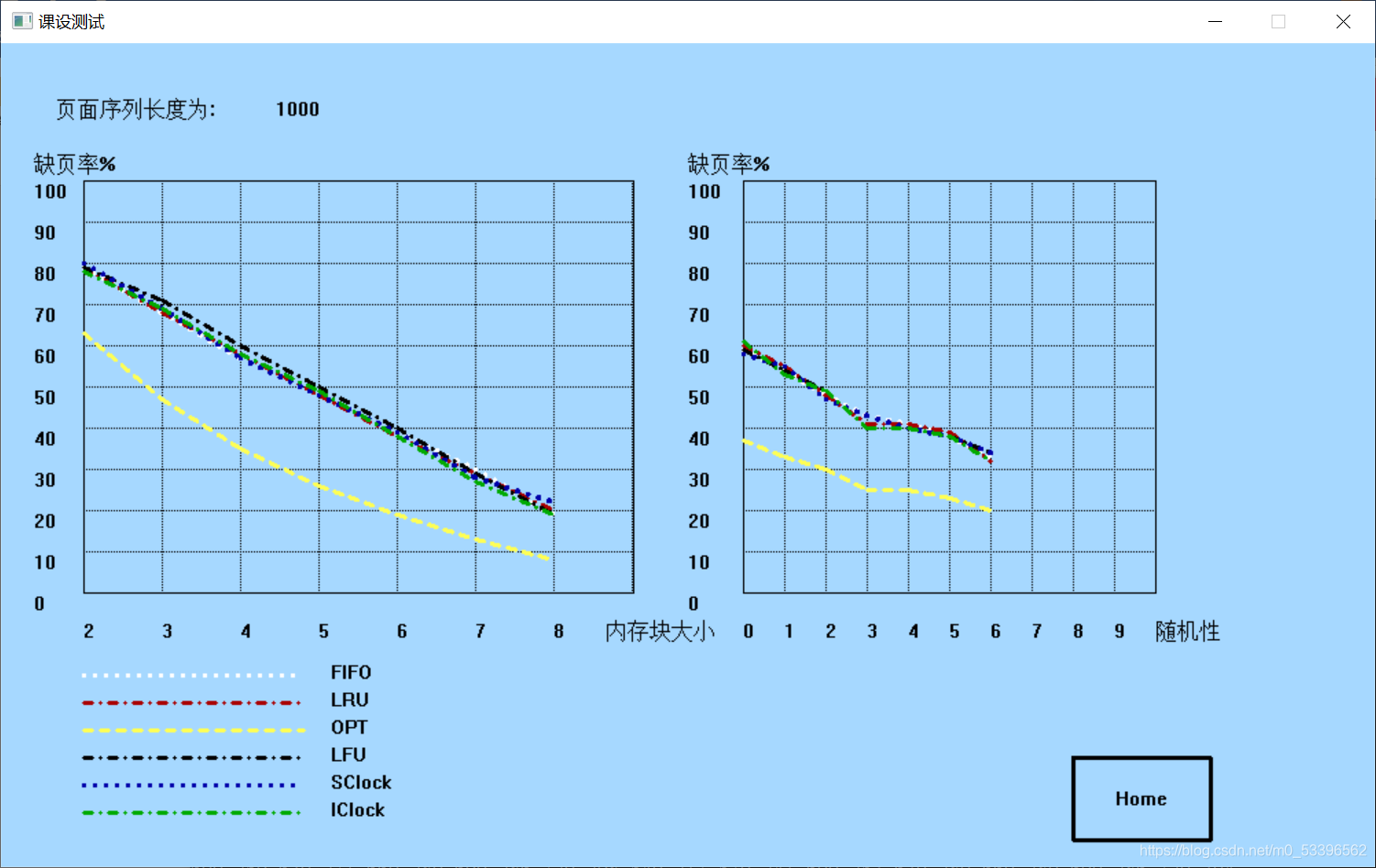
?(可见,当页面序列足够长(1000)时,OPT作为一种理论上的算法,确实厉害嗷)
3、最后。如果按照课程设计的要求,做完上述“框架”的内容 并且生成一幅类似上图的曲线图,课设已经完成任务了。但我出于对初识easyx的新鲜感,为整个程序做了一个图形化界面。(花了许多不必要的时间)
展示部分截图:
?
?![]()
?
到这里,我的课程设计就全部完成了
四、结语
?由于本人敲代码能力确实有限,加之时间紧促,没有进行优化。整个包含图形化界面的代码有将近2k行,这里就不展示了。如有需要(?)可联系up邮箱:1660584637@qq.com
这是本人第一次发布博客,若其中有错误之处恳请各位批评指正,有疑问的地方也欢迎一起讨论,感谢各位!