老师推荐人工智能最简单入手的是octave,用它写出来之后再转用python、c++会更方便。
简介
GNU Octave is a high-level language primarily intended for numerical computations. It is
typically used for such problems as solving linear and nonlinear equations, numerical linear
algebra, statistical analysis, and for performing other numerical experiments. It may also
be used as a batch-oriented language for automated data processing.
GNU Octave是一种高级语言,主要用于数值计算。它通常用于求解线性和非线性方程、数值线性代数、统计分析等问题,以及进行其他数值实验。它也可以用作自动化数据处理的面向批处理的语言。
这只是做个简单入门,更多的功能可以看一下官方文档:octave.pdf
基本
-
注释 %
- 类似于C++的//和python的#
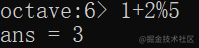
-
ans 用于存储输出结果
-
如果你不喜欢输入行前缀,可以自定义修改
PS1('你想改成的内容');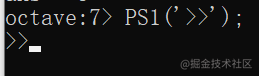
这个不是永久的,你电脑重启之后他又恢复默认了。
-
help帮助
如果你忘了某一个语句的用法了,可以用这个查询。比如输入
help eye就会显示eye的用法。
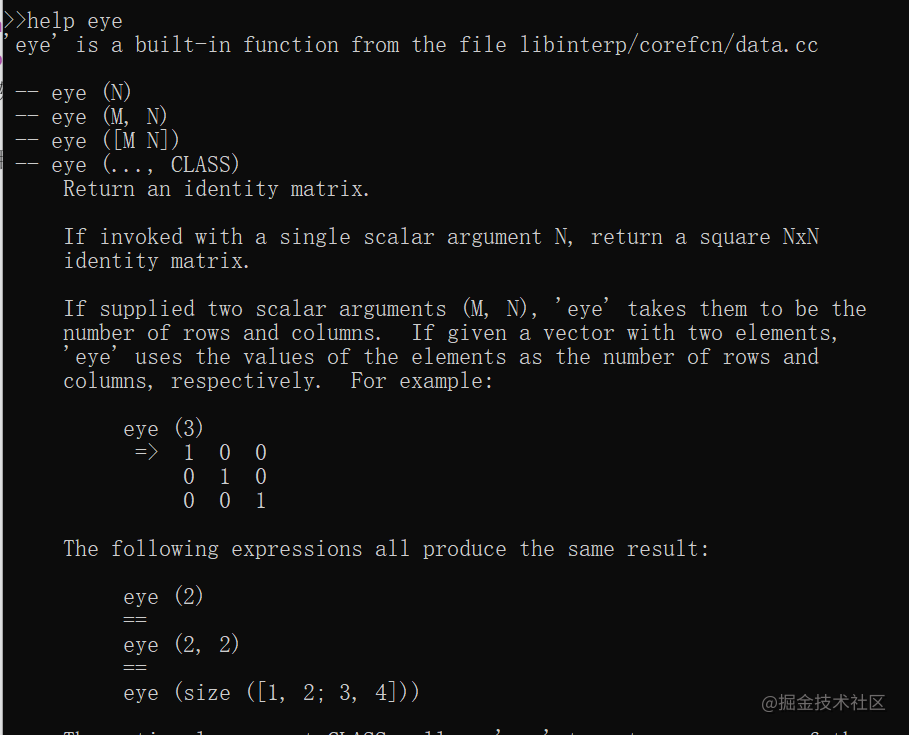
5.多个语句同时执行用逗号分开即可。
c octave:226> a=4,b=5,c=6 a = 4 b = 5 c = 6
符运算
算术运算符
加减乘除乘方
octave:1> 1+5
ans = 6
octave:2> 1*5
ans = 5
octave:3> 1/5
ans = 0.2000
octave:4> 1-5
ans = -4
octave:5> 5^2
ans = 25
逻辑运算符
- 等于
== - 不等于
~= - 或
|| - 与
&& - 异或
xor(a,b) - 大于等于
>= - 大于
>
ans = 0
>>1==1
ans = 1
>>1 ~=2
ans = 1
>>1&&2
ans = 1
>>1&&0
ans = 0
>>1||0
ans = 1
>>xor(1,1)
ans = 0
>>xor(1,2)
ans = 0
>>xor(0,1)
ans = 1
>>1>=2
ans = 0
>>1<2
ans = 1
赋值运算符
=赋值运算符- 语句后边加分号 不直接打印赋值语句
- 语句后边不加分号 直接打印赋值语句
>>a=1 %a=1后边没分号,所以输入回车之后下一行会直接打印a=1
a = 1
>>a %再输入a回车看看是否赋值成功
a = 1
>>b=2; %b=2后边加上分号了,所以下一行不会直接打印b的赋值
>>b %输入b回车,查看给b的赋值
b = 2
>>c=pi
c = 3.1416
格式化输出
disp(x):显示x的值disp(sprintf('%0.2f',c)):格式化输出保留两位小数,这个和C语言一样format long/short:对整数无影响,对小数输出格式有影响
>>disp(a)
1
>>disp(c)
3.1416
>>disp(sprintf('%0.2f',c))
3.14
>>format long
>>a
a = 1
>>c
c = 3.141592653589793
>>format short
>>a
a = 1
>>c
c = 3.1416
向量和矩阵
声明矩阵官方原话写的是:
Vectors and matrices are the basic building blocks for numerical analysis. To create a new matrix and store it in a variable so that you can refer to it later, type the command
octave:1> A = [ 1, 1, 2; 3, 5, 8; 13, 21, 34 ]
Octave will respond by printing the matrix in neatly aligned columns.
>>martix = [1,2,3;4,5,6;7,8,9]
martix =
1 2 3
4 5 6
7 8 9
当然还有很多其他写法,虽然不规范也能声明矩阵,这里就不列举了。
声明行向量,各个元素之间不用加符号,或者加逗号。
martix =
1 2
2 3
3 4
>>vector=[1 2 3]
vector =
1 2 3
>>vector = [4;5;6]
vector =
4
5
6
其他特殊写法:
-
变量 = 起始:步长:终止,就会生成一个向量 ,
,
-
ones(a,b)生成a行b列只有1的矩阵
- 除了
ones还有zeros,生成的元素都是0,但是没有twos、threes……
-
rand(a,b) 生成a行b列的0-1之间随机数的矩阵
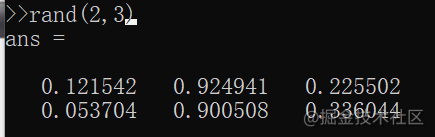
max(rand(n),rand(n))生成量个方阵,取其中较大值形成一个新方阵octave:124> c = max(rand(4),rand(4)) c = 0.8010 0.9926 0.7241 0.9053 0.9007 0.3026 0.9856 0.5710 0.7679 0.2630 0.5200 0.9615 0.7333 0.5113 0.6957 0.5683
-
randn(a,b)也是生成a行b列随机数矩阵,但是符合高斯分布(正态分布)。返回一个具有正态分布随机元素的矩阵,这些随机元素的平均值为零,方差为1。- 正态分布:
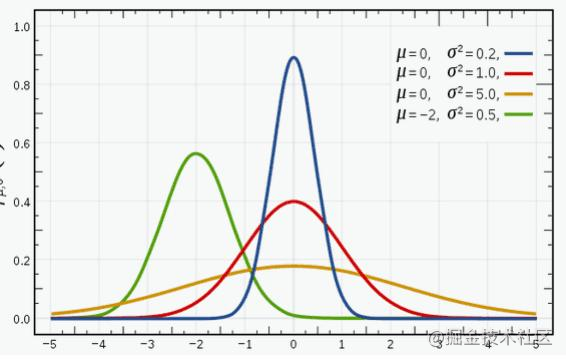
- 正态分布:
-
randi()- randi(max,m,n):生成1~max的m行n列矩阵
- randi([min,max],m,n):生成min~max的m行n列矩阵

-
eye(n)生成n维单位矩阵 -
matrixB = matrixA(x:y,v:w):将matrixA的x~y行v~w列形成一个新矩阵:表示所有元素a:b表示a到b的元素[a b c]表示abc三行或列- 以上三种表示方法在矩阵别的方法中也能使用,比如赋值、打印
-
矩阵拼接
- 在矩阵右侧添加一列
octave:30> A A = 4 2 7 5 1 10 7 10 5 10 9 9 octave:31> A = [A,[2;4;5]] A = 4 2 7 5 2 1 10 7 10 4 5 10 9 9 5 matrixC=[matrixA matrixB]横向拼接
写[matrixA, matrixB]也一样,加不加逗号都行octave:33> A = randi(5,2,3) A = 4 1 3 2 3 5 octave:34> B = randi(5,2,3) B = 5 4 5 1 1 3 octave:35> c = [A B] c = 4 1 3 5 4 5 2 3 5 1 1 3matrixC=[matrixA; matrixB]纵向拼接octave:33> A = randi(5,2,3) A = 4 1 3 2 3 5 octave:34> B = randi(5,2,3) B = 5 4 5 1 1 3 octave:36> d=[A;B] d = 4 1 3 2 3 5 5 4 5 1 1 3
- 在矩阵右侧添加一列
-
matrix(:)将矩阵中的所有元素放入一个列向量octave:30> A A = 4 2 7 5 1 10 7 10 5 10 9 9 octave:31> A(:) ans = 4 1 5 2 10 10 7 7 9 5 10 9 2 4 5
其他
-
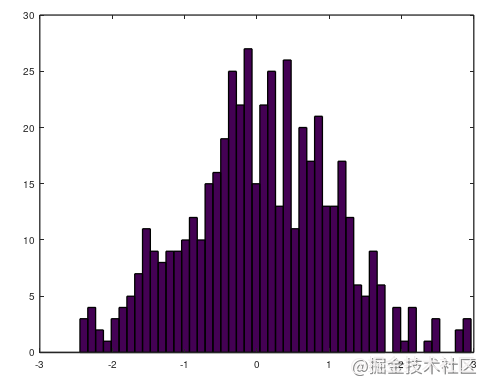
hist(变量)可以画出变量的图像

如果你觉得这样太少了。那可以使用
hist(变量,条纹数),下图就是画出50条纹后的图像。
-
检测大小
size()length()
下图可以看出,length显示矩阵的长度。size显示矩阵有几行几列。size(矩阵名称,1/2)其中1代表行参数,2代表列参数。

-
索引:
matrix(i,j)显示第i行第j列的元素octave:26> A = randi(10,3,4) %生成一个1~10之间随机数的 3×4 的矩阵 A = 4 2 7 5 1 10 7 10 5 10 9 9 octave:27> A(2,3) %打印这个矩阵2行3列的元素 ans = 7matrix(:,[a,b,c...])::代表全部[]:方括号中有哪几个就选中哪几个-
octave:26> A = randi(10,3,4) A = 4 2 7 5 1 10 7 10 5 10 9 9 octave:27> A(:,[1,2,4]) %显示A所有行的1,2,4列 ans = 4 2 5 1 10 10 5 10 9
-
显示现有变量
who:显示目前所有变量whos:显示目前所有变量和详细信息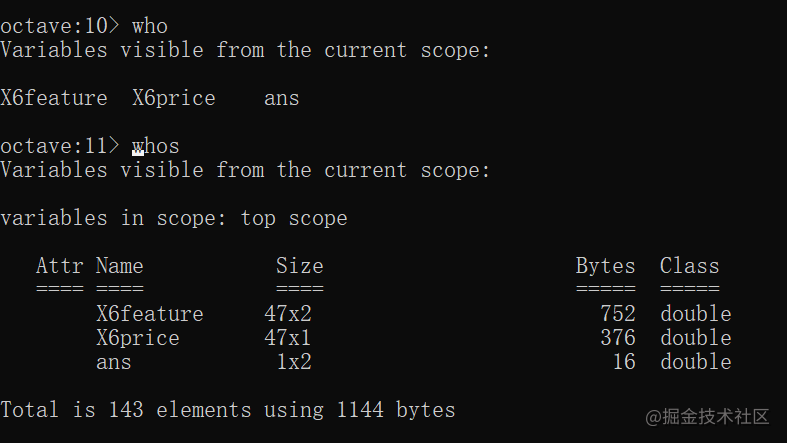
-
删除某个变量
clearclear 变量删除三个变量- `clear 删除所有变量
octave:12> a = 15 % 给a赋值15 a = 15 octave:13> a % 打印a a = 15 % 显示a的值 octave:14> clear a octave:15> a % 再次打印a error: 'a' undefined near line 1, column 1 %报错
移动数据
用过其他命令行的应该能适应,octave也同样支持某些命令。
pwd:列出当前目录cd xxx文件夹:进入xxx文件夹ls:列出当前目录信息- 加载文件:
load 文件名load('文件名')
- save 文件名 变量; :将变量保存到文件中,比如
save data.txt num,把num变量保存到data.txt中(如果操作目录中没有这个文件会创建一个新文件,如果目录中有这个文件会重写)
下边给出两个文件的数据,featureX和priceY,自己搞两个文件存起来。
featureX:
2104 3
1600 3
2400 3
1416 2
3000 4
1985 4
1534 3
1427 3
1380 3
1494 3
1940 4
2000 3
1890 3
4478 5
1268 3
2300 4
1320 2
1236 3
2609 4
3031 4
1767 3
1888 2
1604 3
1962 4
3890 3
1100 3
1458 3
2526 3
2200 3
2637 3
1839 2
1000 1
2040 4
3137 3
1811 4
1437 3
1239 3
2132 4
4215 4
2162 4
1664 2
2238 3
2567 4
1200 3
852 2
1852 4
1203 3
priceY:
399900
329900
369000
232000
539900
299900
314900
198999
212000
242500
239999
347000
329999
699900
259900
449900
299900
199900
499998
599000
252900
255000
242900
259900
573900
249900
464500
469000
475000
299900
349900
169900
314900
579900
285900
249900
229900
345000
549000
287000
368500
329900
314000
299000
179900
299900
239500
首先进入对应的操作目录。
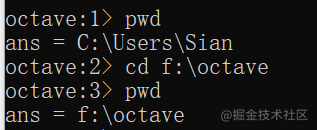
用who查看当前有的变量。
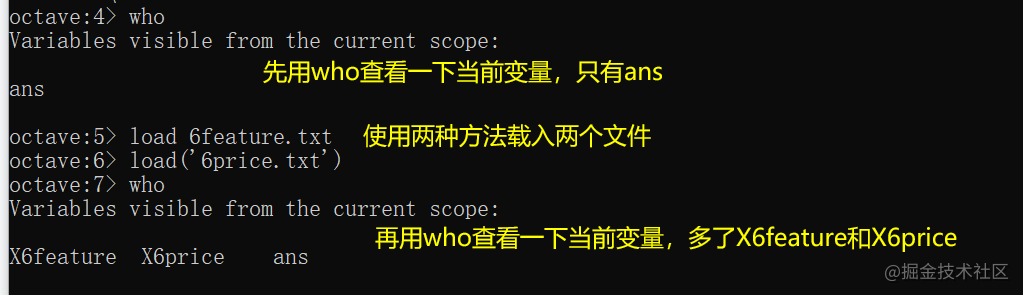
打印依稀下X6price确实已经成功读入文件

用size查看一下,导入的数据是存在矩阵中的。
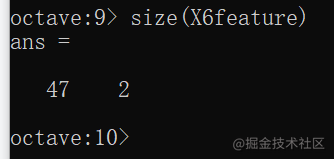
把矩阵X6feature的1~5行,第2列 赋值给矩阵x,并将矩阵x保存到data.txt中
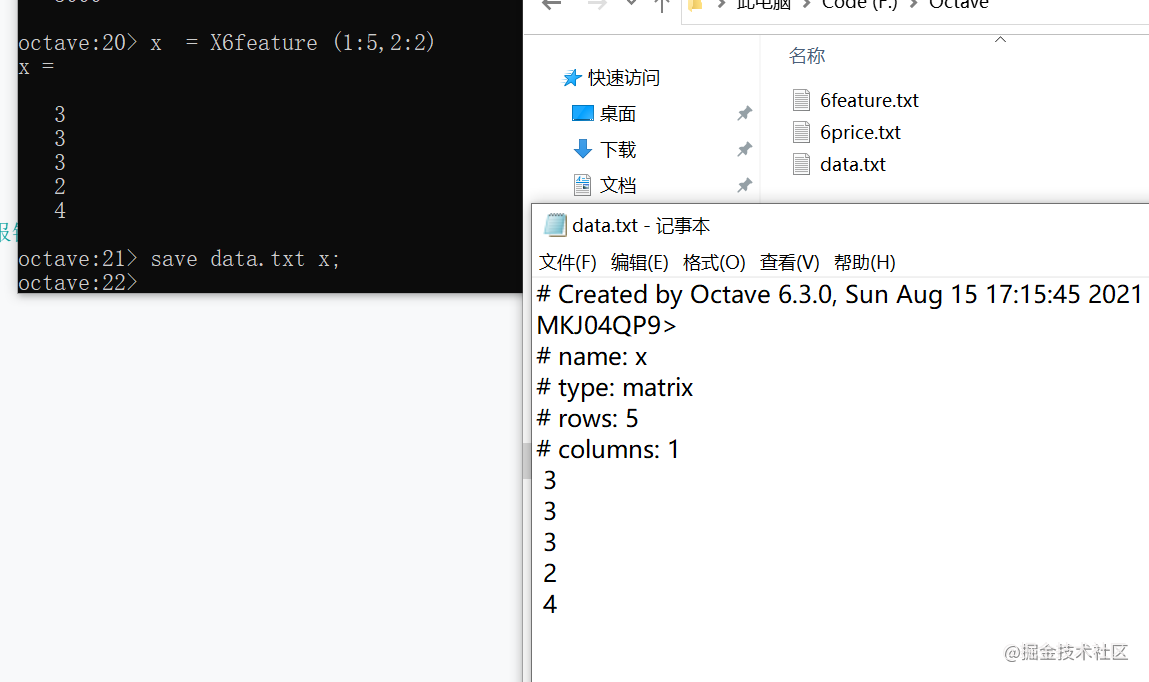
计算
除了最开始提到的算术运算符,还有以下运算。
注意一个特殊的.*,矩阵同位相乘,即矩阵相同位置上的元素相乘。
octave:37> A
A =
4 1 3
2 3 5
octave:38> B
B =
5 4 5
1 1 3
octave:39> A * B %AB无法相乘
error: operator *: nonconformant arguments (op1 is 2x3, op2 is 2x3)
octave:40> A .* B %AB可以点乘
ans =
20 4 15
2 3 15
.^给矩阵每个元素做乘方
octave:43> A
A =
4 1 3
2 3 5
octave:44> A .^2
ans =
16 1 9
4 9 25
octave:45>
矩阵/数即可让矩阵的每个元素都除以该数字,但是如果你想让一个数除以矩阵的每个元素,结果仍旧是矩阵,那就需要./
octave:38> B
B =
5 4 5
1 1 3
octave:50> 2 ./B
ans =
0.4000 0.5000 0.4000
2.0000 2.0000 0.6667
如果想让矩阵每个元素都加或减去一个数,直接用+-即可。
octave:71> C
C =
2 -1 -4 1
-5 -2 -1 -1
1 -1 -5 -4
octave:72> C+1
ans =
3 0 -3 2
-4 -1 0 0
2 0 -4 -3
octave:73> C-2
ans =
0 -3 -6 -1
-7 -4 -3 -3
-1 -3 -7 -6
octave:74> 1+C
ans =
3 0 -3 2
-4 -1 0 0
2 0 -4 -3
log(n)这里的log底数是e,即
log
?
e
n
\log_en
loge?n或
ln
?
n
\ln n
lnn
octave:57> log(2)
ans = 0.6931
octave:58> log(e)
ans = 1
octave:59> A
A =
4 1 3
2 3 5
octave:60> log(A)
ans =
1.3863 0 1.0986
0.6931 1.0986 1.6094
exp(n)相当于执行
e
n
e^n
en
octave:61> exp(1)
ans = 2.7183
octave:62> exp(2)
ans = 7.3891
octave:63> A
A =
4 1 3
2 3 5
octave:64> exp(A)
ans =
54.5982 2.7183 20.0855
7.3891 20.0855 148.4132
abs()求绝对值
octave:66> C = randi([-5,2],3,4) %随机生成一个3×4的矩阵,取值在-5\~2之间
C =
2 -1 -4 1
-5 -2 -1 -1
1 -1 -5 -4
octave:67> abs(-1)
ans = 1
octave:68> abs(C)
ans =
2 1 4 1
5 2 1 1
1 1 5 4
matrix'转置,矩阵名称后加英文单引号
octave:75> C
C =
2 -1 -4 1
-5 -2 -1 -1
1 -1 -5 -4
octave:76> C'
ans =
2 -5 1
-1 -2 -1
-4 -1 -5
1 -1 -4
flipud使矩阵垂直翻转。就是左边变右边,右边变左边。
result1 =
17 0 0 0 0
0 5 0 0 0
0 0 13 0 0
0 0 0 21 0
0 0 0 0 9
octave:140> flipud(result1)
ans =
0 0 0 0 9
0 0 0 21 0
0 0 13 0 0
0 5 0 0 0
17 0 0 0 0
矩阵<数值大于啊等于啊都同理。会返回一个同纬度的矩阵,每个元素都是对应位置元素进行比较返回的布尔值
a =
1 5 3 4
octave:85> a<2
ans =
1 0 0 0
magic(n)生成n阶幻方,所谓幻方就是行、列、对角线加起来都是相同的值
octave:95> magic(4)
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
octave:96> magic(3)
ans =
8 1 6
3 5 7
4 9 2
find(公式)
- 找到向量中符合的数据并返回其索引
a = 1 5 3 4 octave:88> find(a<3) ans = 1 octave:89> find(a>2) ans = 2 3 4 - 找到矩阵中符合的数据
C = 9 7 3 5 4 2 5 10 4 1 9 10 octave:114> [r,c]=find(C==1) r = 3 c = 2 octave:115> [r,c]=find(C>7) r = 1 3 2 3 c = 1 3 4 4
sum()求和prod()求积
c =
1
3
4
4
octave:117> sum(c)
ans = 12
octave:118> prod(c)
ans = 48
floor()向下取整ceil()向上取整
a =
0.5000
1.5000
2.0000
2.0000
octave:120> floor(a)
ans =
0
1
2
2
octave:121> ceil(a)
ans =
1
2
2
2
max(矩阵)取最大值
如果是矩阵,那就显示每一列的最大值;如果是向量,那就只显示一个最大值
v=max(matrix):将矩阵的最大值赋给v,不是硬性要求,v可以换别的名称[v,i]=max(matrix):将矩阵最大值及其位置赋值给v和imax(max(matrix)):取得整个矩阵最大值max(matrix(:)):取得整个矩阵最大值,这个是将矩阵转化成响亮之后再求最大值
c =
2 1 4 1
5 2 1 1
1 1 5 4
octave:78> val = max(c)
val =
5 2 5 4
octave:79> [val,ind]=max(c)
val =
5 2 5 4
ind =
2 2 3 3
max(矩阵,[],1/2) 取得矩阵每一行或者列的最大值形成一个向量
- 1 取每一列
- 2 取每一行
c =
8 9 7 9
9 3 9 5
7 2 5 9
7 5 6 5
octave:129> max(c,[],1)
ans =
9 9 9 9
octave:130> max(c,[],2)
ans =
9
9
9
7
小练习:
生成一个幻方,然后测试其每行,每列,对角线之和都是同一个数
octave:131> m = magic(5) %生成一个5×5的幻方
m =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
octave:132> sum(m,1) %每列相加都是65
ans =
65 65 65 65 65
octave:133> sum(m,2) %每行相加都是65
ans =
65
65
65
65
65
octave:135> e=eye(5) %生成一个单位矩阵
e =
Diagonal Matrix
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
octave:136> result1 = e .* m %单位矩阵同位相乘原矩阵,新矩阵只剩主对角线元素
result1 =
17 0 0 0 0
0 5 0 0 0
0 0 13 0 0
0 0 0 21 0
0 0 0 0 9
octave:139> sum(result1(:)) %主对角线相加为65
ans = 65
octave:141> result2 = m .* flipud(e)
result2 =
0 0 0 0 15
0 0 0 14 0
0 0 13 0 0
0 12 0 0 0
11 0 0 0 0
octave:142> sum(result2(:)) %副加为65
ans = 65
pinv()求逆矩阵
m =
8 1 6
3 5 7
4 9 2
octave:145> pinv(m)
ans =
0.147222 -0.144444 0.063889
-0.061111 0.022222 0.105556
-0.019444 0.188889 -0.102778
绘图
plot(A,B)A是横坐标向量,B纵坐标
octave:173> t=[-1:0.01:1];
octave:174> p1 = sin(2*pi*t);
octave:175> plot(t,p1)
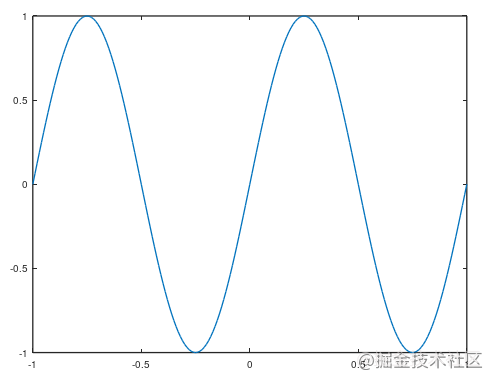
octave:176> p2 = cos(2*pi*t);
octave:177> plot(t,p2)
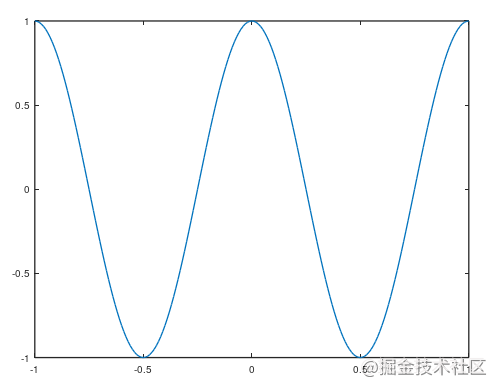
画完一张图以后想要画另一张就会重新绘制,用hold on可以保留,在原图基础上继续画,并且会自动给你切换颜色。
octave:177> plot(t,p2)
octave:178> hold on
octave:179> plot(t,p1)
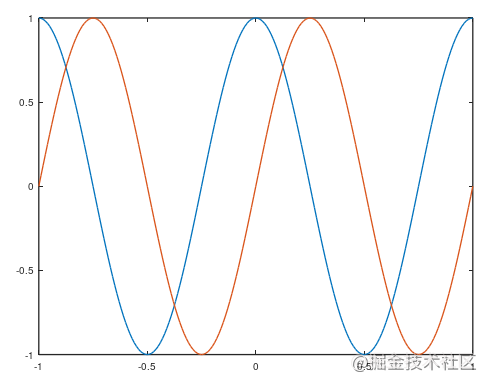
给横轴纵轴添加标签。
octave:183> xlabel('time')
octave:184> ylabel('speed')
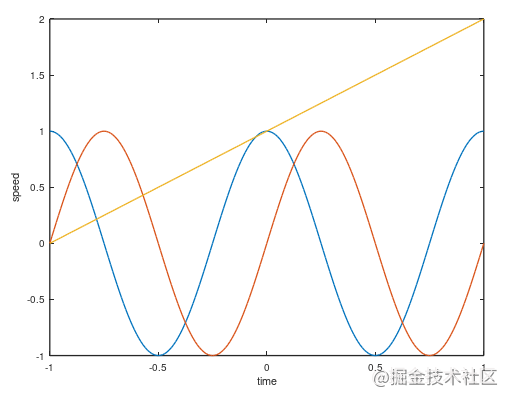
添加图例
legend('cos','sin','y')
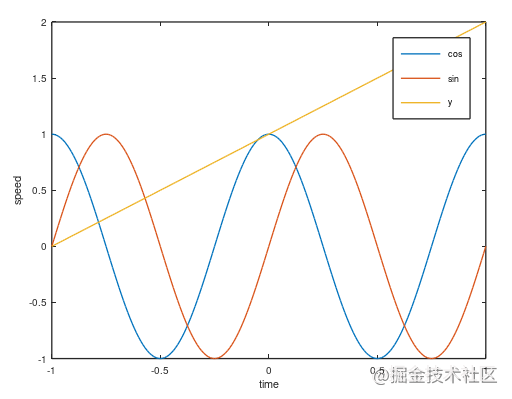
添加标题
title('my demo')
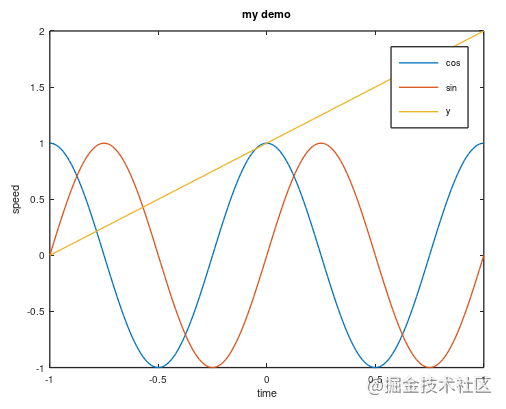
保存文件
print -dpng '文件名'
保存之后你的当前目录下边就会多出一个图片。如过你不知道当前目录是啥,输入pwd查看当前目录的路径。
如果你想同时生成多个图片,那在前边加上figure(n);则会按顺序生成图片。
octave:194> figure(1);plot(t,p1)
octave:195> figure(2);plot(t,p2)

合并显示图像subplot(n,m,index),将图像分成n行m列,取index位置绘图。
octave:197> subplot(2,3,4)
octave:198> plot(t,p1)
octave:199> subplot(2,3,2)
octave:200> plot(t,p2)
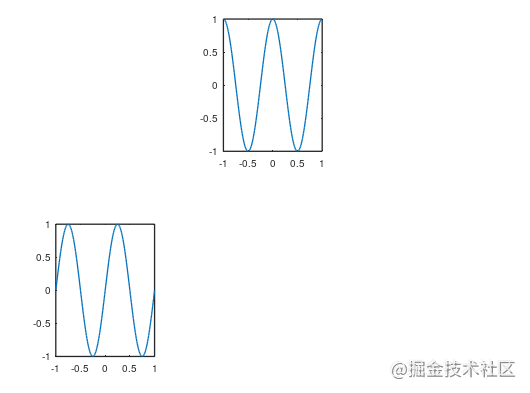
改变纵横轴取值范围axis([横轴起始 终止 纵轴起始 终止])
octave:203> subplot(1,2,1)
octave:204> plot(t,p2)
octave:205> subplot(1,2,2)
octave:206> plot(t,p2)
octave:207> axis([0 1 -2 2])
下图两个是同一副图,右边是改变坐标轴范围之后的图像。
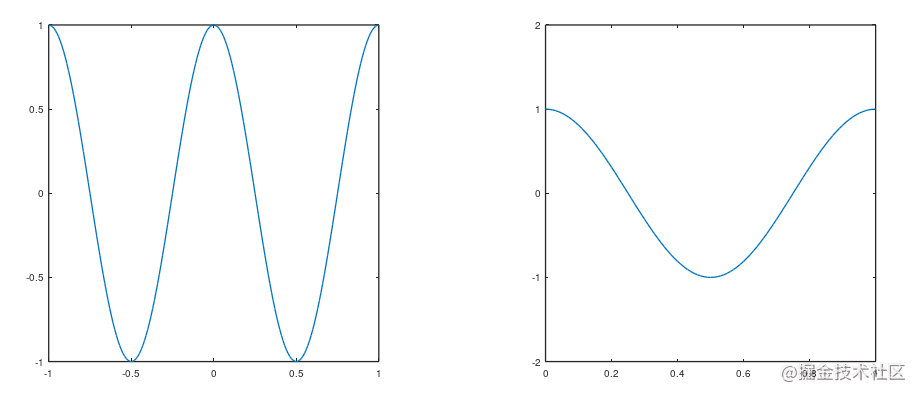
clf清空整幅图,close不用点右上角×关闭图像
矩阵可视化
imagesc()
a =
8 1 6
3 5 7
4 9 2
octave:217> imagesc (a)

说个题外话,作为一个曾经的生物学生,我好像突然get到了我们以前的热图是怎么出来的。
octave:218> load 6feature.txt % 还记得这组数据吗,就是我上边给的那两组数据的第一组。
octave:219> imagesc (X6feature)
画出来以后图像长这样,恩我真的get到热图怎么画的了。
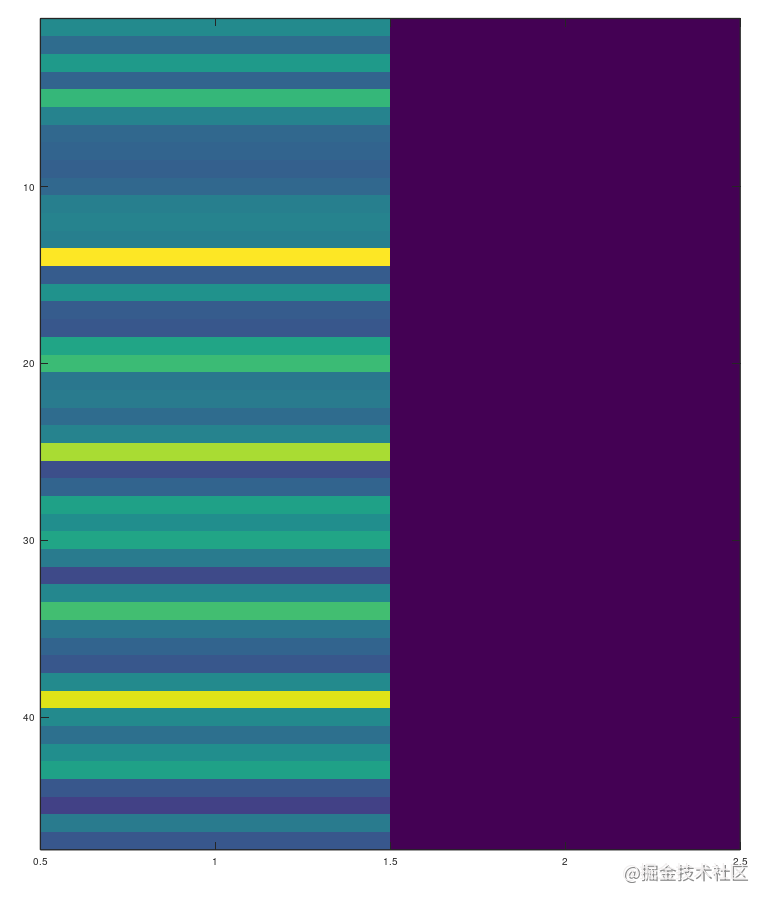
现在让我们生成一个热图(假的,不是热图,看起来像而已)
octave:220> r = rand(5,50);
octave:221> imagesc (r)

colorbar添加比色的图例。
octave:223> colorbar
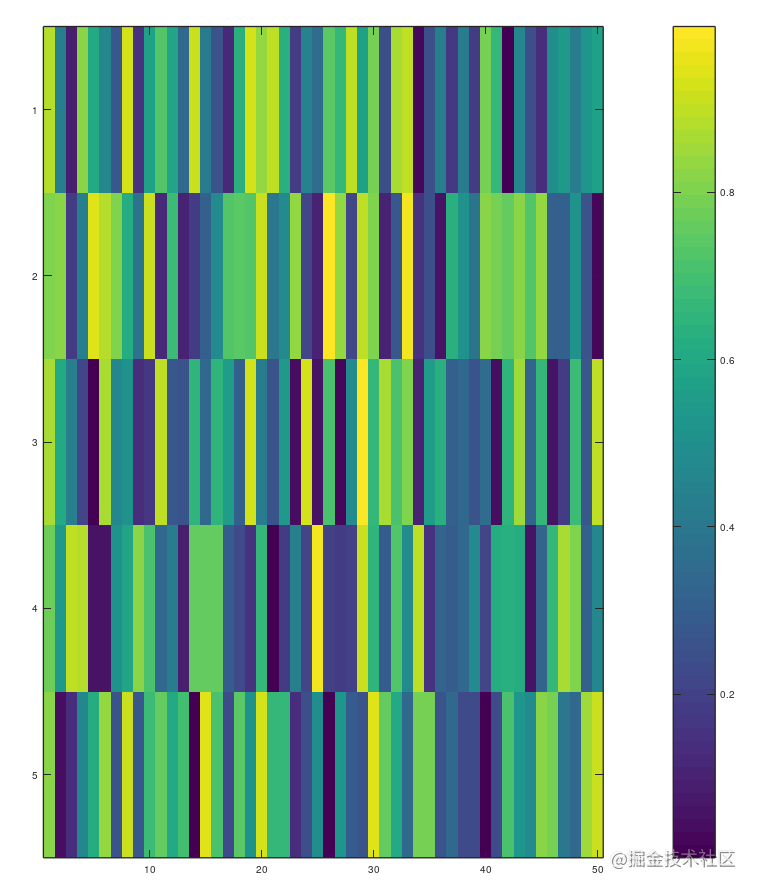
colormap gray使其变为灰度图
colormap gray

