在水电站优化运行中,水轮机的动力特性曲线,需要根据离散的特征点拟合得到。拟合方法有多项式拟合、径向基函数神经网络拟合等,其中多项式最小二乘拟合,是最经典、最简单的一种方法。本文在水电站优化运行的应用背景下,研究了多项式最小二乘拟合的算法,给出了 Delphi/Pascal 实现。
目录
1 多项式最小二乘拟合

算法?1?多项式最小二乘拟合

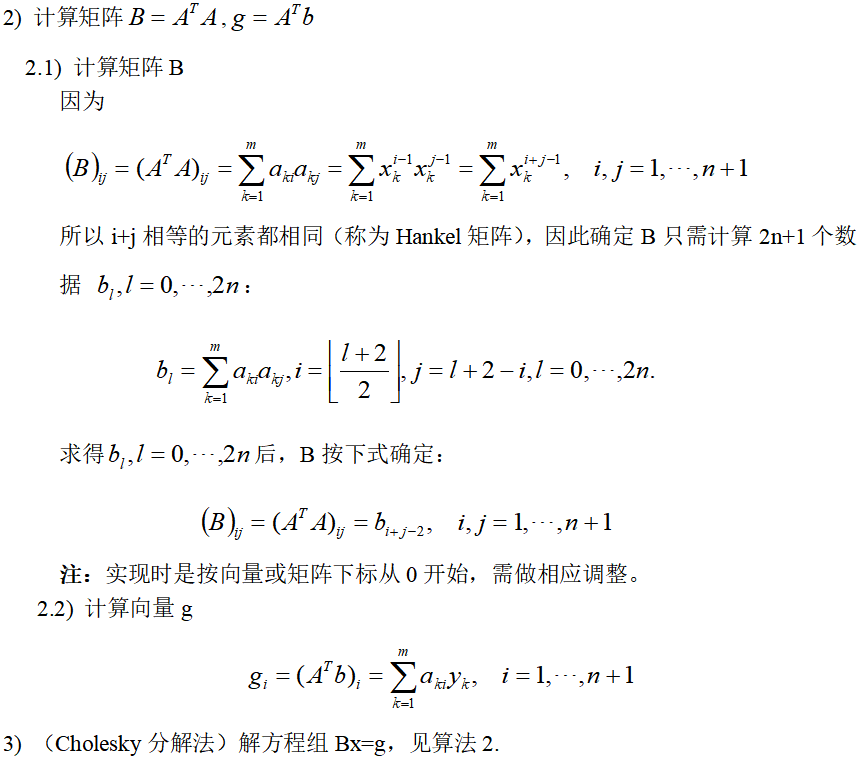
2? Cholesky分解法解方程组
算法2 ?Cholesky分解法解方程组Ax=b,?参见[1, P60]
输入:对称正定矩阵A,向量b

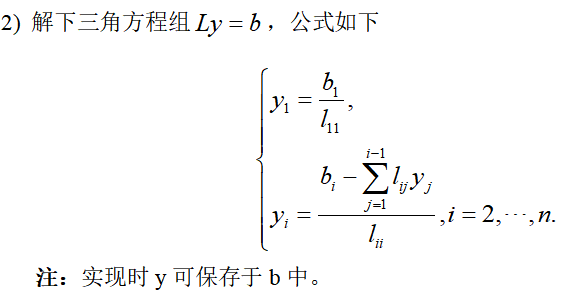
?
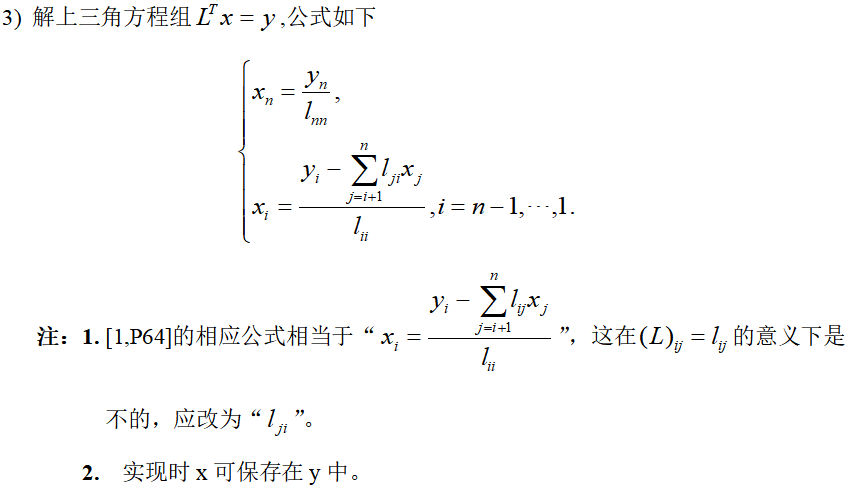
3 数值试验
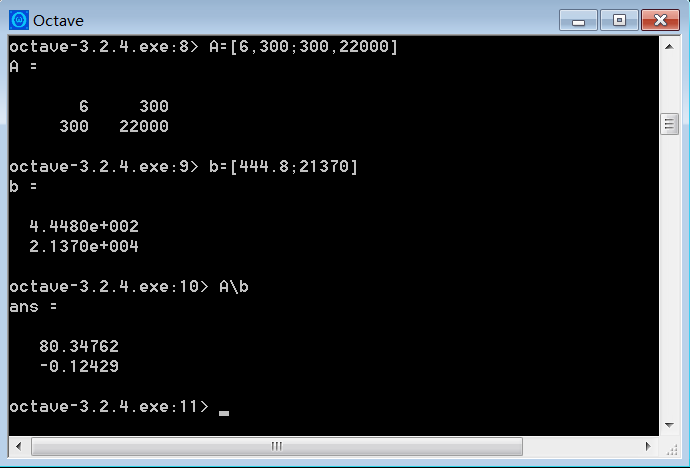
采用文献[1,P304]中例3进行测试,PolyFit计算得结果为(80.34762, -0.12429),而[1]中结果为(80.3463,-0.12427),有较大出入。为确定正确结果,采用通用科学计算自由软件?GNU Octave?计算,得到结果如下图所示,与PolyFit结果相同,从而算法实现的正确性得到了初步验证。要进一步测试本程序的稳定性可以找更多有代表性的例子,与通用计算软件进行比较。
参考文献
[1]?郑慧娆,陈绍林,莫忠息,黄象鼎.?数值计算方法[M].?武汉大学出版社,2002.
?
源程序:(基于 Delphi 实现)
多项式最小二乘拟合
unit PolyFit;
interface
uses
VectorMatrix;
type
TPolyCurveFit = class
private
FN: Integer; // 拟合多项式阶数;
FM: Integer; // 离散数据点数;
FX: TVector; // 离散点横坐标;
FY: TVector; // 离散点纵坐标;
FPolyCoef: TVector; // 拟合多项式系数;
public
constructor Create(aOrder, aDataNum: Integer; aDataX, aDataY: TVector);
procedure Compute;
published
property Order: Integer read FN;
property PolyCoef: TVector read FPolyCoef;
end;
implementation
uses
Math,
Cholesky;
constructor TPolyCurveFit.Create(aOrder, aDataNum: Integer; aDataX, aDataY: TVector);
begin
FN := aOrder;
FM := aDataNum;
SetLength(FX, FM);
SetLength(FY, FM);
FX := Copy(aDataX);
FY := Copy(aDataY);
end;
procedure TPolyCurveFit.Compute;
var
A, AA: TMatrix; // A, A^T * A;
Ab: TVector; // A^T * b, b即向量FY;
AAElem: TVector; // AA 的所有元素;
I, J, K, L: Integer;
begin
// 计算矩阵 A;
SetLength(A, FM, FN + 1);
for I := 0 to FM - 1 do
begin
A[I, 0] := 1;
for J := 1 to FN do
begin
A[I, J] := A[I, J-1] * FX[I];
end;
end;
// 计算矩阵 AA;
SetLength(AAElem, 2*FN + 1);
for L := 0 to 2*FN do
begin
I := Floor(L / 2.0);
J := L - I;
AAElem[L] := 0;
for K := 0 to FM-1 do
AAElem[L] := AAElem[L] + A[K, I] * A[K, J]
end;
SetLength(AA, FN + 1, FN + 1);
for I := 0 to FN do
for J := 0 to FN do
AA[I, J] := AAElem[I + J];
// 计算向量 Ab;
SetLength(Ab, FN + 1);
for I := 0 to FN do
begin
Ab[I] := 0;
for K := 0 to FM - 1 do
Ab[I] := Ab[I] + A[K, I] * FY[K];
end;
// Cholesky 分解法解线性方程组 AA * x = Ab;
SetLength(FPolyCoef, FN + 1);
FPolyCoef := Copy(CholeskySolve(FN + 1, AA, Ab));
end;
end.Cholesky分解法解线性方程组
unit Cholesky;
interface
uses
VectorMatrix;
function CholeskySolve(aN: Integer; A: TMatrix; b: TVector): TVector;
implementation
{ Cholesky分解解线性方程组 Ax=b ;
输入:
aN:阶数;
A:系数矩阵,为 aN*aN 阶正定矩阵;
b:aN阶向量;
返回:aN阶解向量,TVector类型,即数组;
}
function CholeskySolve(aN: Integer; A: TMatrix; b: TVector): TVector;
var
X: TVector;
I, J, K: Integer;
TmpNum: Double;
begin
if aN < 2 then
Exit;
// Cholesky分解 A = G * G^T, G 保存在A的下三角部分;
// 计算 G 首列(第0列);
if A[0,0] <= 0 then
Exit;
A[0, 0] := Sqrt(A[0, 0]);
for I:= 1 to aN - 1 do
A[I, 0] := A[I, 0] / A[0, 0];
// 计算 G 其他列;
for K := 1 to aN - 1 do
begin
TmpNum := 0;
for J := 0 to K-1 do
TmpNum := TmpNum + A[K, J]* A[K, J];
TmpNum := A[K, K] - TmpNum;
if TmpNum <= 0 then
Exit;
A[K, K] := Sqrt(TmpNum);
if K < aN-1 then
for I := K+1 to aN-1 do
begin
TmpNum := 0;
for J := 0 to K-1 do
TmpNum := TmpNum + A[I, J] * A[K, J];
{ 2012-04-15,hll
严重bug修正, PolyFit测试程序中二阶方程测试成功为巧合;
}
//A[K, K] := (A[I, K] - TmpNum) / A[K, K];
A[I, K] := (A[I, K] - TmpNum) / A[K, K];
end;
end;
// 求解下三角方程组 G * y = b;
SetLength(X, aN);
X[0] := b[0] / A[0, 0];
for I := 1 to aN-1 do
begin
TmpNum := 0;
for J := 0 to i-1 do
TmpNum := TmpNum + A[I, J] * X[J];
X[I] := (b[I] - TmpNum) / A[I, I];
end;
// 求解上三角方程组 G^T * x = y;
X[aN-1] := X[aN-1] / A[aN-1, aN-1];
for I := aN-2 downto 0 do
begin
TmpNum := 0;
for J := I + 1 to aN - 1 do
TmpNum := TmpNum + A[J, I] * X[J];
X[I] := (X[I] - TmpNum) / A[I, I];
end;
Result := X;
end;
end.源码和文档(因为比较小,可执行程序也包含在内,还可以运行,但发现结果不正确。时过境迁,原因不明),放在百度网盘,供参考。
下载地址:https://pan.baidu.com/s/1DsuzGnCx1zqyIqrCrgugNg
提取码:3az1